融合高阶信息的社交网络重要节点识别算法

2019-11-03闫光辉张萌罗浩李世魁刘婷

通信学报 2019年10期

闫光辉，张萌，罗浩，李世魁，刘婷

（兰州交通大学电子与信息工程学院，甘肃兰州 730070）

1 引言

信息技术的多元化发展，使人们日常交流、互动的形式趋于多样化，由此产生了海量的社交网络数据[1]。社交网络数据存在着大量人和人之间的交互信息，在这些数据中挖掘具有影响力的节点能够帮助人们在理解传播模式的基础上，更好地引导或阻止信息的传播。

节点重要性是节点影响力、地位或者其他因素的表现形式之一[2]。节点的重要性评价方法大体可以分为以下4 类。1)基于节点近邻的排序方法，这类方法主要关注节点的邻居信息。例如度中心性（DC,degree centrality）[3]，它是根据一个节点的邻居数目来判断该节点的影响力，这种方法能够简单直观地刻画节点的重要性。但是，由于没有考虑网络的全局结构，在多数情况下不够精确[4-6]。2)基于路径的排序方法，此类方法中，节点在传递过程中的重要程度决定着节点的重要性[4]。介数中心性（BC,betweenness centrality）[7]和接近中心性（CC,closeness centrality）[8]是基于路径的2 种经典方法。BC 通过在2 个节点之间所有的最短路径中计算某个节点的路径占总路径的比例，来刻画该节点在网络中的控制能力[4]。CC 通过一个节点与网络中其他节点的平均距离得到节点的重要性。CC 值越大，说明该节点在网络中对控制信息的流动越有意义[4]。虽然它们通过全局结构更好地识别了影响力更大的节点，但是计算复杂较高，很难应用于大规模网络。3)基于特征向量的排序方法，主要代表有PageRank 算法[9]和LeaderRank 算法[10]。它们通过模拟用户上网浏览网页的过程，使节点的分值沿着访问路径增加，来识别网页重要性[4]。4)基于节点移除和收缩的排序方法，其特点是网络的结构会随着重要节点排序的过程处于动态变化中，节点的重要性通过该节点被移除之后对网络的破坏程度来体现[4]。

尽管上述文献针对不同情况对网络中节点的重要性进行了度量，但是它们都是以节点和边为基本单元的研究方法。这些方法都忽略了在真实社交网络中存在于节点之间的高阶关系。大量研究表明，社交网络包含着丰富的子图结构，这些子图结构内部具有一定的传递性、交互性、平衡性等特性。人们一般将这种子图结构描述成网络模体或者图元结构[11-14]。同时，相较于以点和边为研究对象的低阶结构，这种以小子图结构为研究单元的网络结构被称为高阶网络结构[15]。自2002 年模体的概念被提出后，人们的研究大多着眼于如何高效地统计网络中模体的数量；直到2016 年，Benson 等[15-16]证明模体可以用于图聚类和社团发现，并提出了一系列的理论基础，高阶网络的研究成为当前研究的重点之一。

为了定量地度量社交网络中节点的重要性，本文将模体作为节点之间高阶关系的研究单元，采用高阶网络分析方法得到基于模体的加权邻接矩阵，进而给出高阶度定义，将节点度和高阶度这2 个独立的信息源融合得到新的基本概率指派，并结合半局部中心性的思想，得到基于高阶结构的重要节点识别方法。最后，在3 个真实社交网络上检验不同重要节点识别方法得到的节点影响力程度。

2 相关概念

2.1 复杂网络中的高阶结构

模体是高阶网络结构的一种表现形式[17]。将原始网络表示为高阶网络结构过程如下。首先，在网络中选定模体，此时，在指定阶数的模体集合中，选取原始网络中出现次数最多的连接形式。文献[17]指出，针对不同领域，网络中呈现的高阶连接结构各有偏重，结合社会学的相关理论选取三阶模体作为研究对象[18-19]。图1 列举了三阶模体的所有存在形式。选定模体阶数后，再对所选阶数的模体逐个进行统计，最终选出原始网络中出现次数最多的模体连接形式。本文采用文献[20]提出的模体检测算法来统计网络中模体的数量。

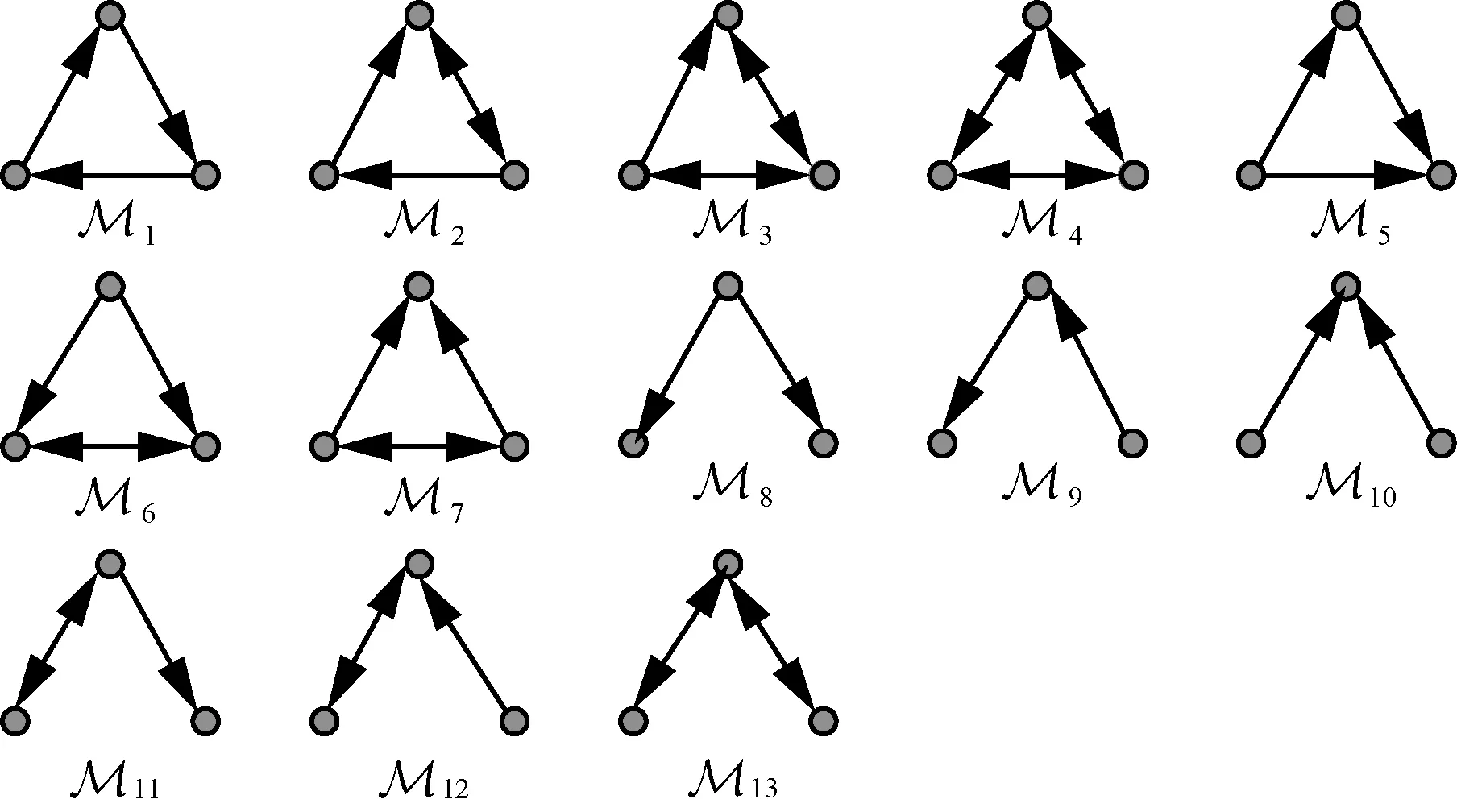
图1 三阶网络模体的所有存在形式

定义1网络模体（network motif）。用一个元组(B,A)表示由k个节点组成的模体。其中，B是k×k的二进制矩阵，矩阵B中的元素代表节点之间是否有连边，A 是一个目标节点的集合，A⊂{1,2,…,k}。一般而言，选取的目标节点是B中所有的节点。图2 表示由3 个节点组成的模体M7。

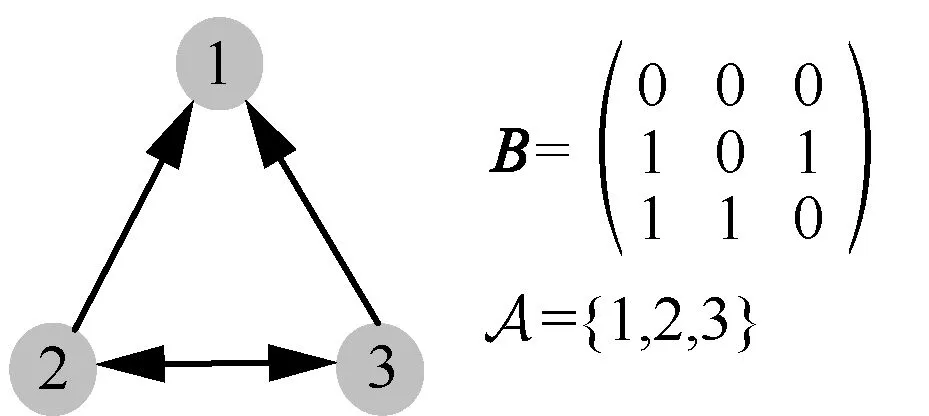
图2 模体7M 的定义

定义2基于模体的邻接矩阵（motif-based adjacency matrix）。给定一个模体M，模体邻接矩阵可以定义为矩阵元素wij为在G中节点对(vi,vj)在选定的模体中出现的次数，可定义为

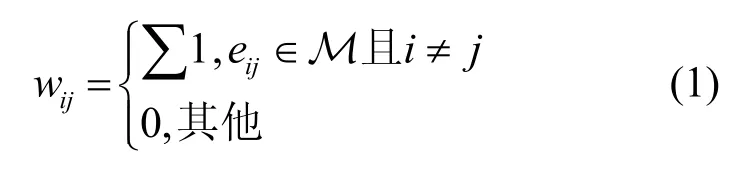
定义3高阶网络（higher-order network）。高阶网络可以表示为G=(V,E,WM)，其中，表示点集，…,m}表示弧集，eij是一条由节点vi指向节点vj的有向边，WM是基于模体M 的加权邻接矩阵。

在社交网络中识别重要个体可以转化为识别用户之间关系构成的图中重要节点的问题。同时，文献[17]指出在不同的场景下，模体的主要存在形式各有偏重。本文以社交网络为研究对象，结合社交网络中三元必包的理论，选取三阶模体中1M～7M 这7 种存在形式作为基本研究单元。

2.2 D-S 证据理论

D-S 证据理论本质是对概率论的一种推广，将概率论中的基本事件空间拓展到基本事件的幂集空间，以便更好地表达事件的不确定性，并在其上建立基本概率指派函数[21-22]。本节内容给出辨识框架以及它的幂集这些概念，并将其拓展到网络中的节点上[5]。

定义4辨识框架（frame of discernment）。Θ={θ1,θ2,…,θ N}是由N个两两互斥的元素组成的有限完备集合，则称Θ为辨识框架。辨识框架是所考察判断的事物或对象的全体集合Θ。Θ的幂集2Θ所构成的集合表示为

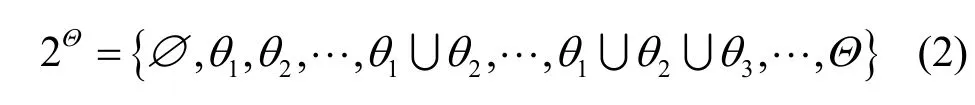
本文将网络中节点是否重要作为考察判断的对象。因此，节点的辨识框架可以定义为其中h和l分别表示节点重要和不重要这2 个互斥的元素。

定义5基本概率指派（BPA,basic probability assignment）。设Θ是辨识框架，Θ的幂集2Θ构成命题集合2Θ，∀A⊆Θ，若函数m:2Θ→[ 0,1]满足以下2 个条件

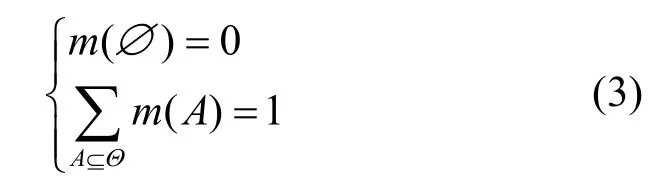
则称m为基本概率指派，m(A)为命题A的基本概率数，即准确分配给A的信度。

定义6Dempster 组合规则。设m1和m2为两组基本概率指派，对应的焦元分别为A1,A2,…,Ak和B1,B2,…,Bl，用m表示m1和m2组合后的新证据。Dempster 组合规则表示为

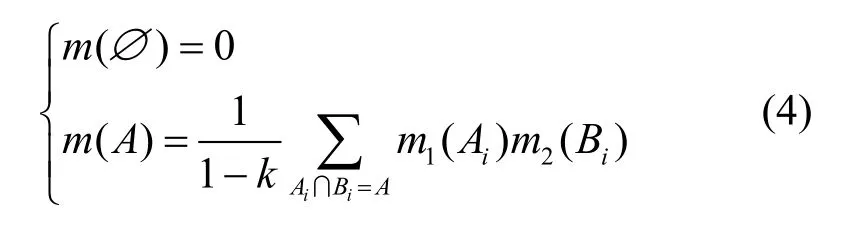
2.3 半局部中心性

半局部中心性（SCL,semi-local centrality）是一种基于半局部信息的节点重要性排序方法，它不仅考虑了节点的直接邻居，还考虑了直接邻居的一阶、二阶邻居数，即最多涉及节点的四阶邻居信息[23]。节点vi的计算过程为

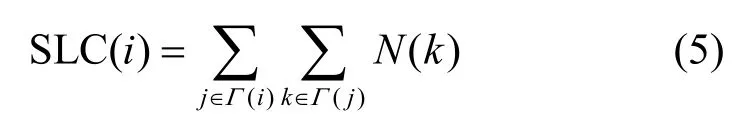
其中，N(k)是节点vk的两层邻居度和，其值等于从vk出发两步内可到达的邻居的数目；Γ(i)是节点vi的一阶邻居节点集合，Γ(j)是节点vj的一阶邻居节点集合。

可见，高阶网络分析方法可以更加具体地表达节点之间的交互关系，在算法复杂度上也有一定的优势。因此，需要考虑如何将高阶信息融合在证据理论中，以达到刻画节点重要性这个模糊概念的目的。

3 基于高阶结构的中心性算法

本节先定义了高阶网络中高阶度的概念，再规定2 个基本的独立信息源，最后将这2 个独立信息源用作证据理论的BPA，融合得到一种高阶证据中心性度量方法。简单来说，该方法不仅考虑了节点的度，还将节点参与网络的程度，即节点的高阶度作为考虑因素。随后，结合半局部中心性的思想对算法进一步优化。相比之前的方法，本文提出的算法不仅考虑了多个节点之间存在的高阶结构，并且结合了半局部中心性的思想。

3.1 高阶度

定义7高阶度（higher-order degree）。节点vi在选定的模体中出现的次数，即在模体邻接矩阵中节点vi在第i行或第i列最大的元素值，记为HDi，即

在高阶网络中，模体邻接矩阵刻画的是节点对(vi,vj)的局部连接密度，其权值越高表示以节点对(vi,vj)为边的模体结构越多，说明该节点对的抗攻击性越差，重要性也就越高。因此，高阶度反映的是节点所在边参与网络的程度。

3.2 定义2 个基本概率指派函数

本文将节点的度和高阶度看作2 种重要性指标，由不同的独立信息源可以得到关于度和高阶度的2 个基本概率指派函数。此时，节点vi的2 个基本概率分布分别为

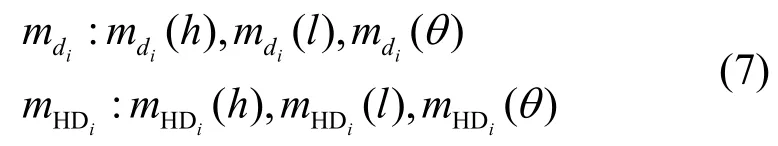
文献[24]用网络中的度分布，对基于度的基本概率指派函数进行改进，得到了一种更符合真实情况的概率指派函数，避免了证据理论计算所得到结果是均匀分布，而真实网络中的节点呈幂律分布这一冲突。因此，基于度和高阶度的BPA 通过式(8)～式(11)计算得到。

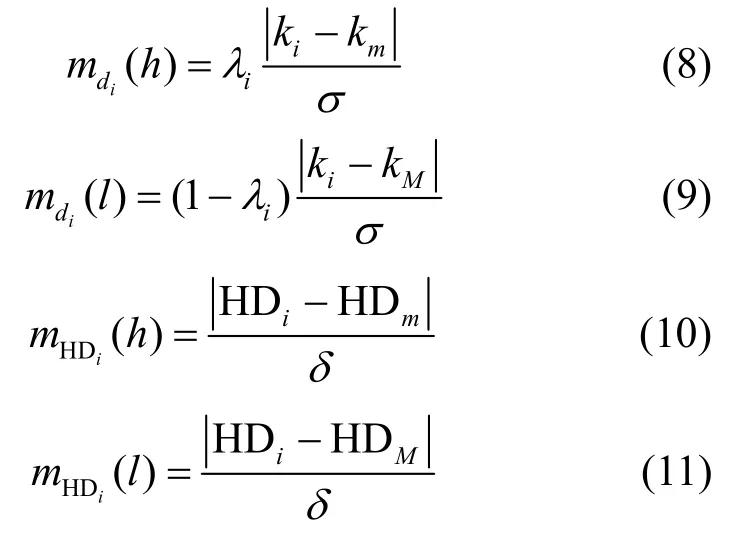
其中，σ和δ分别通过式(12)和式(13)计算得到。

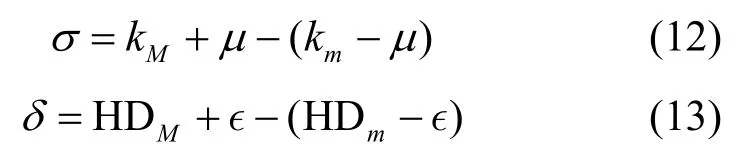
此时，0＜μ,ε1≤ 。文献[5]指出和ε 的取值对节点的排序没有影响。

引入Dempster 证据合成规则，将节点的度和高阶度融合在一起形成一个新的指标M(i)。

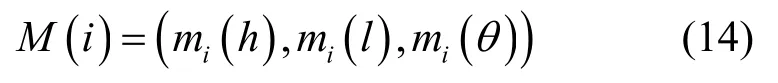
通过式(4)分别计算节点重要的基本概率指派mi(h)、节点不重要的基本概率指派mi(l)和不确定节点是否重要的基本概率指派m i(θ)。通常情况下，为了计算方便将m i(θ)的值平分给mi(h)和mi(l)，得到M i(h)和M i(l)。此时，Mi(h)和M i(l)分别代表节点重要和节点不重要的信任程度。对于一个节点来说，M i(h)越大，同时M i(l)越小，节点的重要性就越大[5]。

3.3 高阶证据中心性

在上述定义的基础上，提出节点的高阶证据中心性（HEC,higher-order evidence centrality）方法。HEC通过节点的重要程度和不重要程度的差值来表示

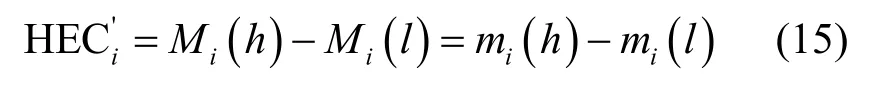
为了确保数值为正，对式(15)进行归一化处理，即

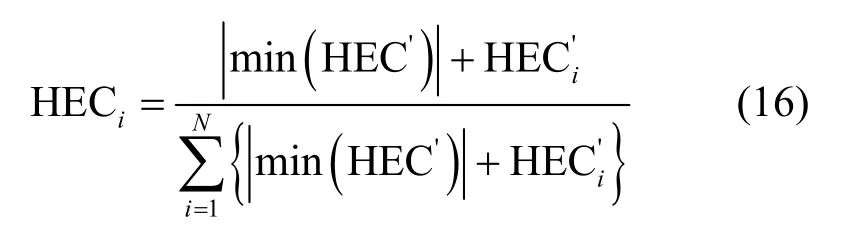
例1图3 所示是一个简单的有向无权图。根据上述定义计算图3 中每个节点的高阶证据中心性值。选取图3 中模体存在形式最多的一种，即7M 。表1 为例1 中所有节点计算高阶证据中心性所需要的相关指标及高阶证据中心性值。本文取μ和ε 的值为0.15。

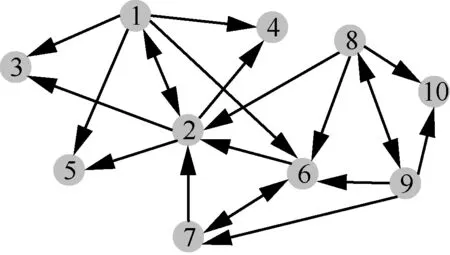
图3 有向无权图的例子

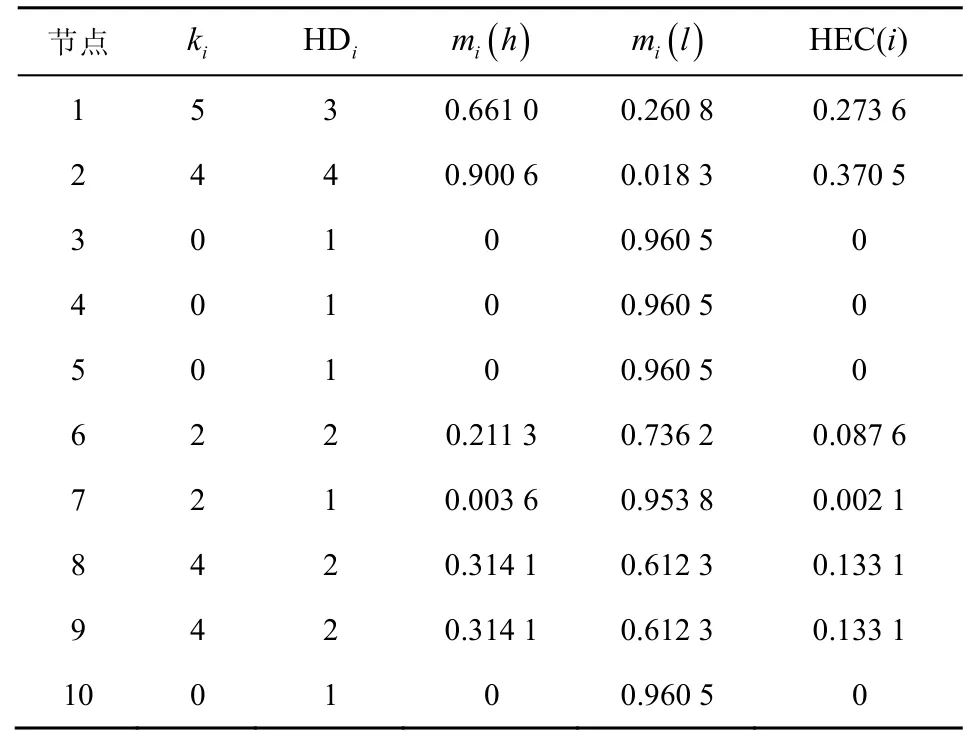
表1 高阶证据中心性计算

3.4 高阶证据半局部中心性

通过上述计算，得到了网络中每一个节点的高阶证据中心性值。为了更精确地表达节点在网络中的传递性，结合半局部中心性的思想，计算网络中每一个节点的直接邻居和直接邻居的两层邻居HEC(i)的和。因此，高阶证据半局部中心性（HESC,higher-order evidence semi-local centrality）为

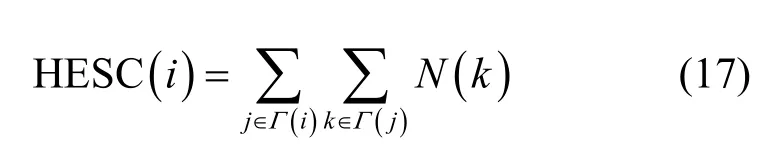
基于高阶结构的HESC 重要节点识别算法如算法1 所示。

算法1HESC 重要节点识别算法

输入有向网络G=(V,E)

输出原始网络中每个节点的HESC 值

1)统计G中的模体，选取模体数量最多的形式M；

2)得到基于M 的加权邻接矩阵WM；

3)for nodeiinVdo:

4)根据式(6)得到HDi；

5)根据式(7)～式(16)计算HEC(i)；

6)根据式(17)计算HESC(i)；

7)end for

8)returnV中每个节点的HESC 值

对于给定的G，网络中节点的个数为n，边的个数为m，文献[20]提出统计原始网络中模体个数的算法，该算法的复杂度为O(m1.5)。半局部中心性由于计算N(k)需要在2 个步骤中遍历节点vk的邻居，因此，时间复杂度为O(n＜k＞2)，即同时考虑了节点直接邻居的一阶和二阶邻居数，其中＜k＞为网络的平均度。证据理论只是在节点本身进行计算，时间复杂度为O(n)。所以，HEC 的时间复杂度为O(m1.5+n)，HESC 的时间复杂度为O(m1.5+n＜k＞2)。表2 给出了本文用到的各算法的时间复杂度。从表2 可以看出，BC 和CC 的时间复杂度过高，不适合大规模网络。

表2 各算法时间复杂度

4 实验

本文采用SIR 模型对上述提出的基于高阶结构的中心性算法进行评价。文献[4]指出SIR 模型是一种基于传播动力学的评价方法，被广泛应用到评价各种节点重要性挖掘方法中。在SIR 模型中，一般通过节点的传播范围和达到稳态时所用的时间作为节点重要性的评判标准。

4.1 SIR 传播模型

SIR 传播模型中的节点在任意时刻都有3 种可能的存在状态：易感染态（S,susceptible）、感染态（I,infected）和恢复态（R,recover）。在t迭代步，这3 类人在人群中的比例分别用S(t)、I(t)和R(t)表示[25]。S(t)代表在一个网络中处于S 状态的节点占比；I(t)代表处于I 状态且能向S 状态节点传播疾病的节点占比，每一个被感染节点都可以通过一定的概率随机地向它的邻居节点传染疾病；R(t)表示感染过疾病但已经恢复且具有免疫能力的节点占比[25]。在复杂网络SIR 模型中，假设被感染的节点周围所有的邻居节点都有机会被感染。在第t个时间迭代步，感染态和恢复态的节点在整个网络中所占的比例F(t)作为传播范围衡量指标。F(t)随迭代次数t的增大而增大，最后趋于稳定。

4.2 数据集描述

Wiki-vote：维基百科为了从用户中选举出词条管理员，通过公开投票的方式选举。该数据集构建的是维基百科用户之间的投票关系网络。网络中的节点代表的是维基百科的用户，有向连边是由投票人指向被选举人。

Advogato：该数据集构建的是Advogato 这个在线社交平台上用户信任关系的有向网络。网络中的节点是Advogato 中的用户，有向边为用户之间的信任关系。

soc-Epinions1：该数据集描述的是消费者在评论网站上的信任关系，是否信任对方由网站上的成员自行决定。由此形成的信任关系网络，可以有针对性地向用户展示消费者的评论。网络中节点代表的是消费者，有向边是消费者之间的信任关系。

表3 展示了上述提到的3 个数据集中节点、边数和模体总数的具体情况。

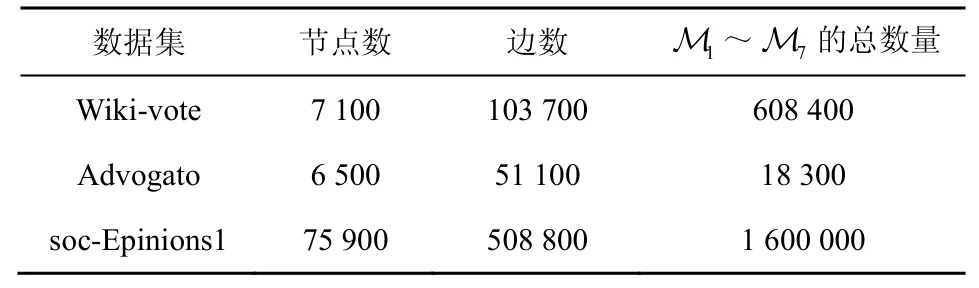
表3 数据集的统计量

同时，对上述3 个数据集上1M～7M 各个模体的数量进行统计。表4 列举了1M～7M 的具体数量。可以看出，本文选取的数据集中模体出现次数最多的形式恰好都是5M 。因为Wiki-Vote 数据集描述的是用户之间的投票关系，5M 可以解释为用户更愿意给自己投过票的人所选举的对象再投出一票。Advogato 和soc-Epinions1 数据集是用户之间的信任关系，5M 可以解释为当一个用户选择信任另一个用户时，后者所信任的用户会作为前者信任的参考对象。因此，在这3 个数据集上选取5M 对原始网络进行处理，得到基于模体5M 的加权邻接矩阵。

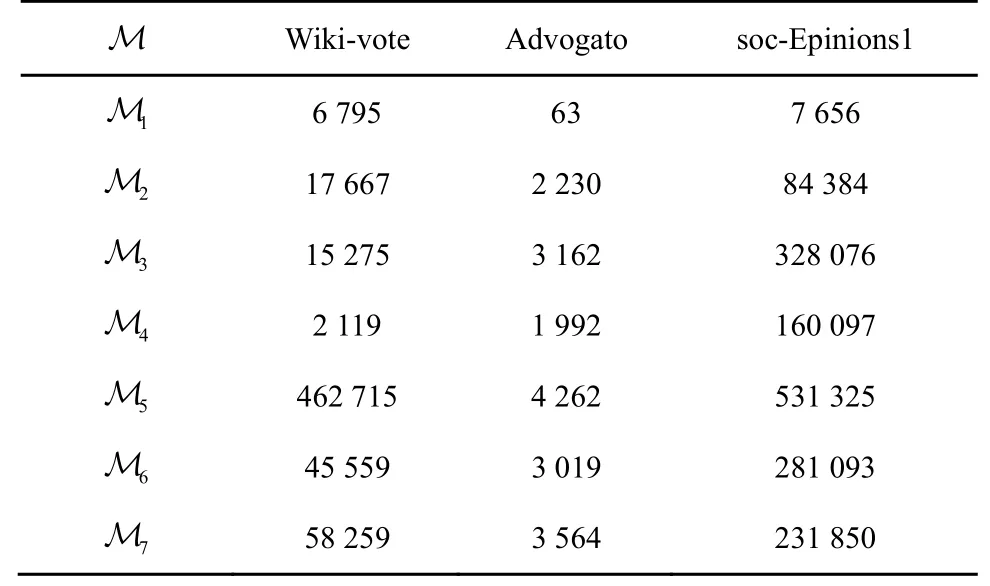
表4 各个数据集中M1～M7的数量

4.3 实验方法介绍

为了比较各排序算法之间的差异性和传播能力，本文选取了经典排序算法DC、BC 和CC 与本文提出的算法进行比较。首先得到各个算法的节点排序，选取各个算法在不同网络上节点排序的Top10、Top20、Top50 和Top100，然后将这些TopN节点作为初始传染源在SIR 模型上进行传播，最后比较传播范围及达到稳态时所用的时间。

4.4 实验结果分析

将3 个数据集上各方法排序中的Top10、Top20、Top50 和Top100 作为SIR 模型中的传染源进行传播，并比较各方法传播的差异性，如图4～图6 所示。

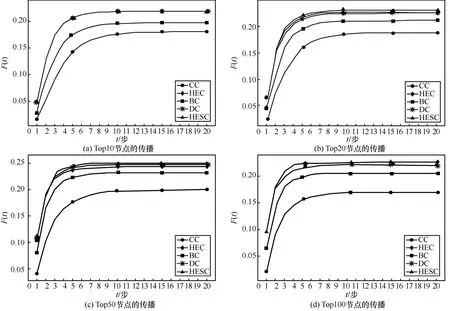
图4 Wiki-vote 数据集TopN 节点的传播

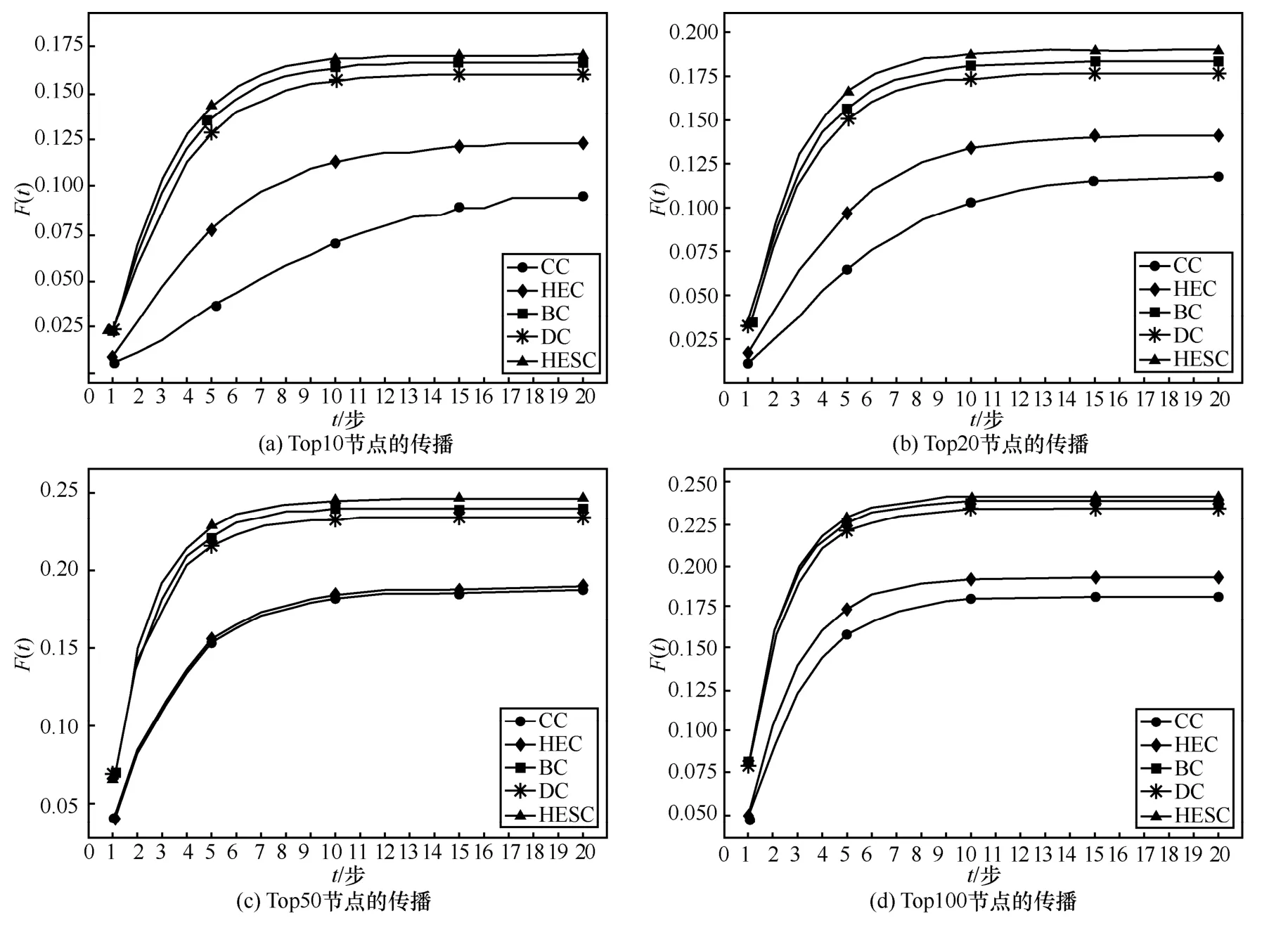
图5 Advogato 数据集TopN 节点的传播

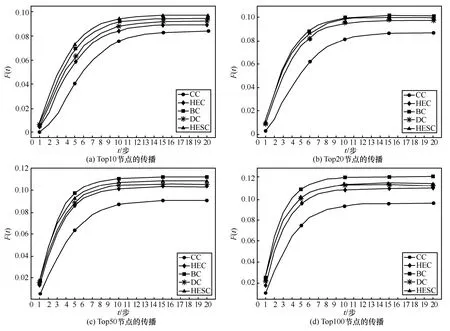
图6 soc-Epinions1 数据集TopN 节点的传播

图4 是Wiki-vote 数据集上各种方法在SIR 模型上的传播。Top10 节点作为传染源进行传播时，本文提出的中心性方法HEC 和HESC 在传播范围和传播速率上基本与DC 相似，如图4(a)所示。但是，从图4(b)～图4(d)可以看出，随着传染源节点的增加，HESC 不管是在传播速率还是传播范围上都好于传统的度量方法，并且网络达到稳态时所用的迭代步最少。

Advogato 数据集上将各种方法得到的节点排序在SIR 模型上传播，可以看出，本文提出的HESC不管是在传播范围还是传播速率都优于经典的方法，如图5 所示。同时还可以看出，本文提出的HESC所得到的排序与BC的结果最为相似。而HEC的方法传播速率和传播范围却相对较差，可能是因为在此数据集中各个模体之间的数量比较接近（如表4 所示），此时以网络中个数最多的模体作为分析对象体现不出该方法的优势。

图6 展示的是soc-Epinions1 数据集上各种方法通过不同TopN节点进行传播的差异性。可以看出，Top10 节点作为传染源进行传播时，HESC 的传播范围和传播效率都比其他方法好，如图6(a)所示。但是，随着传染源节点的增多，HESC 的优势逐渐减退，BC 的传播范围和传播速率优势突显，如图6(b)～图6(d)所示。

对上述不同数据集实验结果分析，虽然本文方法HESC 能够筛选出更重要的节点，但是针对不同的网络存在一定的差异性。在soc-Epinions1 网络中只有当选取Top10 节点作为传染源时，传播能力才会好于其他排序结果，其原因可能是该网络中强连通子图连接的节点比较多，而BC 是基于路径的排序方法。所以，当选取的传染源节点较多时，BC的优势就显现出来。

图7 展示的是静态攻击下从网络中移除TopN节点时，网络中最大连通子图相对大小的变化。横坐标表示从网络中移除TopN节点，纵坐标表示网络中最大连通子图的相对大小。最大连通子图的相对大小是强连通子图连接的节点个数占总节点数的比例。可以看出，当移除TopN节点时，BC 得到的节点排序相较于HESC 对网络的破坏程度更大，所以才会出现图6 中随着传染源节点的增加，BC的传播能力好于HESC 的现象。

表5 列举的是在soc-Epinions1 网络上，各种方法得到的Top10 节点。本文通过Top1 节点在原始网络中的自我中心网络展示其在网络中的重要程度，如图8 所示。自我中心网络是指以一个节点为中心，由其直接相连的节点和这些节点之间的连边组成的网络结构[26]。图8 中处于中间位置直径较大的节点是各种方法得到的Top1 节点，即v18、v44和v645，周围直径较小的节点是Top1 节点的出度所相连的节点。显然，本文提出的中心性方法得到的节点连接了更多的节点，即在网络中所处的位置更为关键。同时，在soc-Epinions1 数据集上，本文提出的方法与BC 方法更为接近的现象也得以说明。

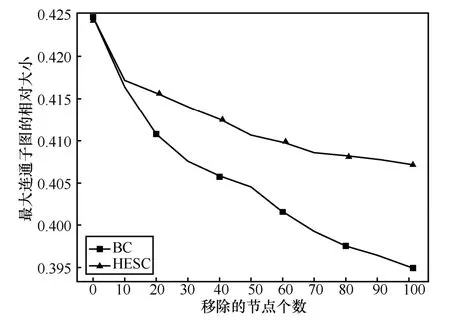
图7 静态攻击下的最大连通子图相对大小

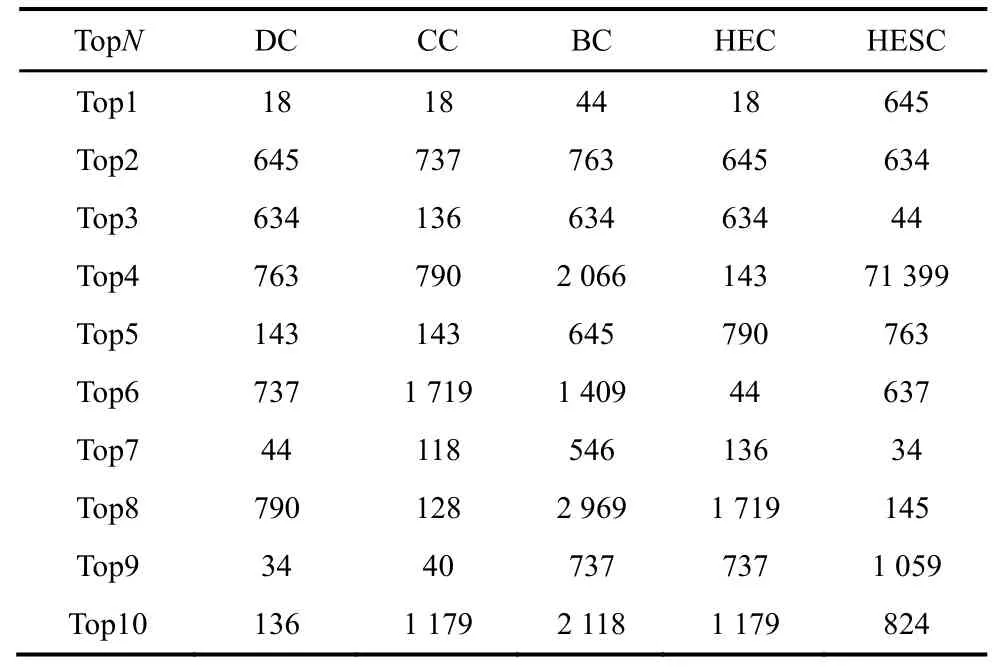
表5 soc-Epinions1 数据集Top10 节点

5 结束语

高阶网络作为一种中尺度的网络结构，相较于从宏观和微观层面入手的研究，高阶网络考虑了节点之间的交互性、传递性等因素。因此，可以更精确地描述网络内部连接的特定模式，同时简化了网络结构。本文主要基于高阶结构提出了重要节点识别算法。该方法以D-S 证据理论为理论基础，融合了高阶网络分析方法，同时，考虑了网络的度分布、半局部中心性。在3 个真实社交网络数据集上，用SIR 模型评价该方法得到的节点重要程度，并与传统的中心性度量方法（DC、BC 和CC）进行对比。通过实验结果分析，本文所提的重要节点识别算法与其他典型的算法相比较，可以更加精确地识别网络中的重要节点。