冷轧损失力矩模型研究

项明武 王志军

力矩是冷轧生产过程中最重要的参数之一。了解力矩各参数的影响规律，并准确预报冷轧的电机力矩，对制定合理的轧制规程，保障设备安全并充分发挥设备能力有积极的意义[1，2]。稳定轧制运行过程中，力矩由有效力矩（轧制力矩）和非有效力矩（损失力矩）构成。有效力矩计算方案比较成熟和准确[3]，非有效力矩在现场中基本被忽略，一般估计为有效力矩或者额定力矩的一定比例[4]。在实际生产中，工艺参数如轧制速度、轧制力等发生变化，非有效力矩其实也是有一定变化规律的，因此这种假设严重限制了力矩模型的准确性[2]。

为此，本文建立了一种基于现场数据的损失力矩计算模型，克服了损失力矩精度无法保证的缺点。基于此方案的力矩模型在江西某冷轧线的实测数据中得到了验证。

1.损失力矩理论模型

冷轧过程主电机力矩由以下五部分构成[4]：

且损失力矩构成如下：

式中：Mm为主电机力矩；M为轧制力矩，用于使轧件发生塑性变形所需的力矩；i表示传动效率；Mf1为克服轧制时发生的轧辊轴承附加摩擦力矩；Mf2为克服轧制时发生的传动机构附加摩擦力矩；Mk为空转力矩，即克服空转时的摩擦力矩；Md为动力矩，即在轧制加减速阶段克服惯性力额外所需的力矩；ML为损失力矩，为轧辊轴承及传动机构的附加摩擦力矩与空转力矩之和，它表示非有效力矩。

以二辊轧机（4个轴承）为例，轧辊轴承附加力矩为：

式中：P为作用在轴承上的负荷，即轧制力；d1表示轧辊辊颈的直径；μ1表示轧辊轴承的摩擦系数。

传动机构摩擦力矩为：

式中：η1表示传动机构的效率；

空转力矩计算比较复杂，一般范围在电机额定转矩的3%～6%。

由理论模型可知，损失力矩各分项计算参数有一些不明确的地方，包括摩擦系数，传动机构效率等。因此无法保证现场力矩计算的精度。

2.损失力矩试验过程与数据处理

2.1 现场热辊试验

在某冷轧厂可逆轧机上进行热辊实验，方案见表1。

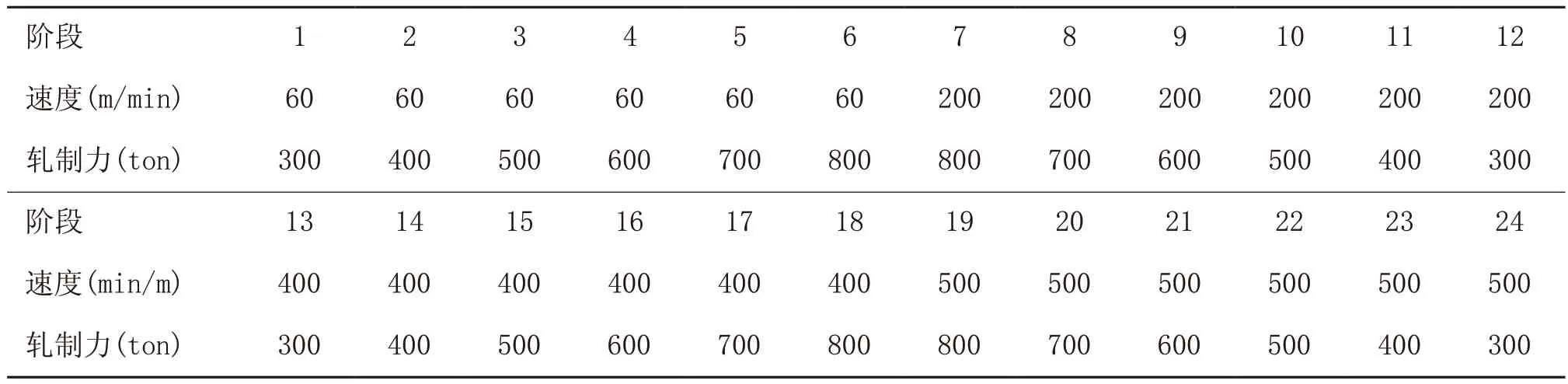
表1 损失力矩实验方案

在轧辊标定完成后，首先进行10分钟基础热辊操作，如阶段1所示，保持轧辊线速度为60m/min，轧制力为300ton。阶段2到24每个阶段历时25s，轧辊线速度和轧制力如表1所示，其中保证稳定运行达到20s，过渡控制在5s以内。整个实验流程共约20分钟。实验过程轧制力变化范围是300ton到800ton，轧制力速度变化范围是60m/min到500m/min。

2.2 数据采集与处理

通过计算机采集轧制力，轧辊线速度，力矩。采集周期为1s。当最近连续15组数据的最大速度与最小速度之差在2m/min以内，且最大轧制力与最小轧制力之差在20ton以内，然后把这15组的速度，轧制力，力矩各取平均值，保存到数据库中。

这种方案能保证各个阶段正好采集到一组最合适的数据。

3.损失力矩经验模型建立

3.1 广义加性模型

广义加性模型(Generalized Additive Model， GAM)由Hastie和Tibshirani在加性模型基础上发展而来，其主要特征在于引入了一个“连接函数”，它与协变量之间建立了关系[5]。

其数学表达式如下：

式中，g(·)为连接函数；a为截距；μ为因变量Y的条件期望；X为自变量；f(·)为单变量函数，且必须是光滑函数；p为自变量个数。

可知，因变量的期望关于自变量是可加的，也就是说它是由各自变量单独相关的光滑函数线性组合而成。显然，广义加性模型易于解释各自变量对因变量的影响关系，其结构简单，且能有效处理理论上并不完善的一些规律函数，因此在各学科均得到一定的应用[5]。

3.2 损失力矩经验模型

由损失力矩理论模型可知，针对具体的某个轧机，损失力矩主要与轧制力和转速相关，采用广义加性模型表示，可知截距为0，且数学表达式如下：

约束条件是：

式中：f1表示转速单变量函数；f2表示轧制力单变量函数；ω是转速，与轧辊线速度和辊径相关；P表示轧制力；

经过探索，具体构建的单变量函数分别如下：

约束条件为：

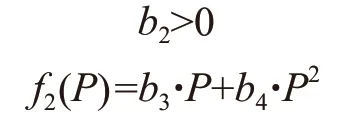
约束条件为：

式中：b0、b1、b2、b3、b4为模型系数。

另外在现场应用较为广泛的日立模型[6]如下，作为对照模型1：

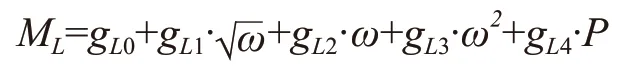
式中：gL0、gL1、gL2、gL3、gL4为模型系数。

基于文献[2]的功率损失模型，其对应的损失力矩模型为对照模型2：

式中：c0、c1、c2为模型系数。

3.3 拟合与结果分析

针对本文建立的数学模型、对照模型1、对照模型2进行拟合，拟合方案采用Levenberg-Marquardt方法[7]（见表2）。

表2 各模型系数的拟合结果

上表可知，对照模型2的建立可能存在不合理之处，在未严格限制参数范围的条件下，拟合过程无法收敛。本文模型和对照模型1都取得了非常好的拟合结果。且本文建立的模型可决系数更好。

以工作辊直径为280mm为例，根据本文模型与对照模型1的损失力矩和速度、轧制力关系见图1所示。

图1 两种模型方案的损失力矩

上图分析可知：本文建立的模型损失力矩对轧制力和速度都是单调递增，符合现场实际。对照模型1在热辊测试的数据范围内（主要是速度60m/min-500m/min）规律与本文建立的模型一致。但是离开测试数据范围，其预报明显不符合实际，说明对照模型1的外延性很差。其主要原因在于，对照模型1速度对损失力矩的影响关系是个简单的多次曲线，计算过程中，在速度较大的时候，速度对损失力矩分项值变为负数，为此非常不符合实际工况。本文的模型基于广义加性模型建模，探索出的一套损失力矩模型除了计算精度很高以外，还具备优秀的外延性。

4.结论

1）建立了一种基于广义加性模型的损失力矩影响模型。

2）模型分析可知损失力矩与轧制速度和轧制力相关，且轧制速度对损失力矩影响较大。

3）开发的损失力矩模型应用于江西某冷轧机组中，通过具体算例验证其具备较高的精度，计算偏差在5%以内，满足在线控制的要求。