发电电动机转子T尾部动载荷作用下的疲劳寿命评估

张宇娇 范虹兴 刘东圆 黄雄峰 姜岚 聂靓靓

摘要：针对抽水蓄能发电电动机运行情况复杂，利用常规的基于静力学计算的疲劳强度校核法和单工况疲劳破坏次数评估法，极易低估疲劳损伤对机组运行年限的累积影响。提出一种动载荷作用下的发电电动机转子T尾部疲劳寿命评估方法。采用结构动力学求得的时变离心应力，与电磁场、温度场计算的电磁应力、热应力叠加得到各工况的动应力载荷谱的方法，结合疲劳实验所得S-N（stress-life）曲线，确定疲劳破坏点及循环次数。根据G-M（gmver-manson）疲劳累积损伤准则，结合已投运年限内的运行数据来预测运行年限。最后，以一台广州蓄能电站已投运机组为例，发现破坏危险点位于转子磁极T尾部，并确定机组的运行年限，验证了该评估方法的正确性。

关键词：发电电动机;转子T尾部;累积疲劳损伤;结构动力学计算;疲劳寿命预测

DoI：10.15938/j.emc.2019.08.014

中图分类号：TV734;TM307文献标志码：A 文章编号：1007-449x（2019）08-0112-10

0引言

发电电动机是抽水蓄能电站的关键设备，其运行状态直接影响电站的运行稳定性。不同于传统水轮发电机，发电电动机运行过程中出现的多次发电启停、电动启停、甩负荷和飞逸工况，将导致转子承受电磁、温度和时变离心力叠加导致的动应力作用。文献[5]的研究发现，当水轮发电机转速达到142.9rev/min，转轮叶片的应力将超过材料的疲劳极限（Crl3Ni4Mo合金为210MPa）。上述复杂工况下，发电电动机转子更易因频繁变化的动载荷导致疲劳损伤而出现破坏，从而引发机组严重的运行故障。研究复杂运行工况下转子动载荷作用下的疲劳损伤及运行年限。无论是已投运机组检修策略的制定，还是机组国产化设计都具有重要意义。

目前，以发电电动机为对象的研究大多集中在变频启动方式研究，电磁一温度场耦合分析，稳态应力分析。然而，由于动力学计算方程和运行年限预测方程复杂，对于发电电动机转子承受动载荷作用下的时变应力分析，以及疲劳运行年限评估方面的研究较少。机组设计制造中为预防结构疲劳破坏采取如下简化方法：基于静力学计算的转子疲劳强度因子校核法;常规单工况疲劳破坏循环次数计算法。考虑到发电电动机的特殊运行情况，常规方法无法准确的评估复杂工况下结构上的动态应力变化过程，和准确预测机组因疲劳破坏出现运行故障的年限。同时，上述2种方法极易低估了发电电动机复杂运行工况下的累积疲劳损伤对机组运行年限缩减的累积影响效应。

为分析复杂工况下频繁变化的时变应力对转子运行年限的累积影响，本文提出了动载荷作用下发电电动机转子T尾部的疲劳寿命预测方法。首先，建立周期性有限元分析模型。随后，采用结构动力学计算各工况下的时变离心力，与电磁一热一结构计算得到的电磁应力、热应力相叠加作为疲劳寿命计算的载荷。设计疲劳实验确定s-N曲线，计算各工况下结构的疲劳寿命。确定疲劳破坏危险点的位置及循环周次。最后，根据G-M（grover-man-son）疲劳累积损伤准则，结合已运行时间内的实际运行数据来预测使用年限。本文选取南方电网广州蓄能电站的一台已投运发电电动机应用动载荷作用下的疲劳寿命评估方法，发现破坏危险点位于转子磁极T尾部，并确定机组的运行年限。

1动载荷作用T疲劳寿命评估方法

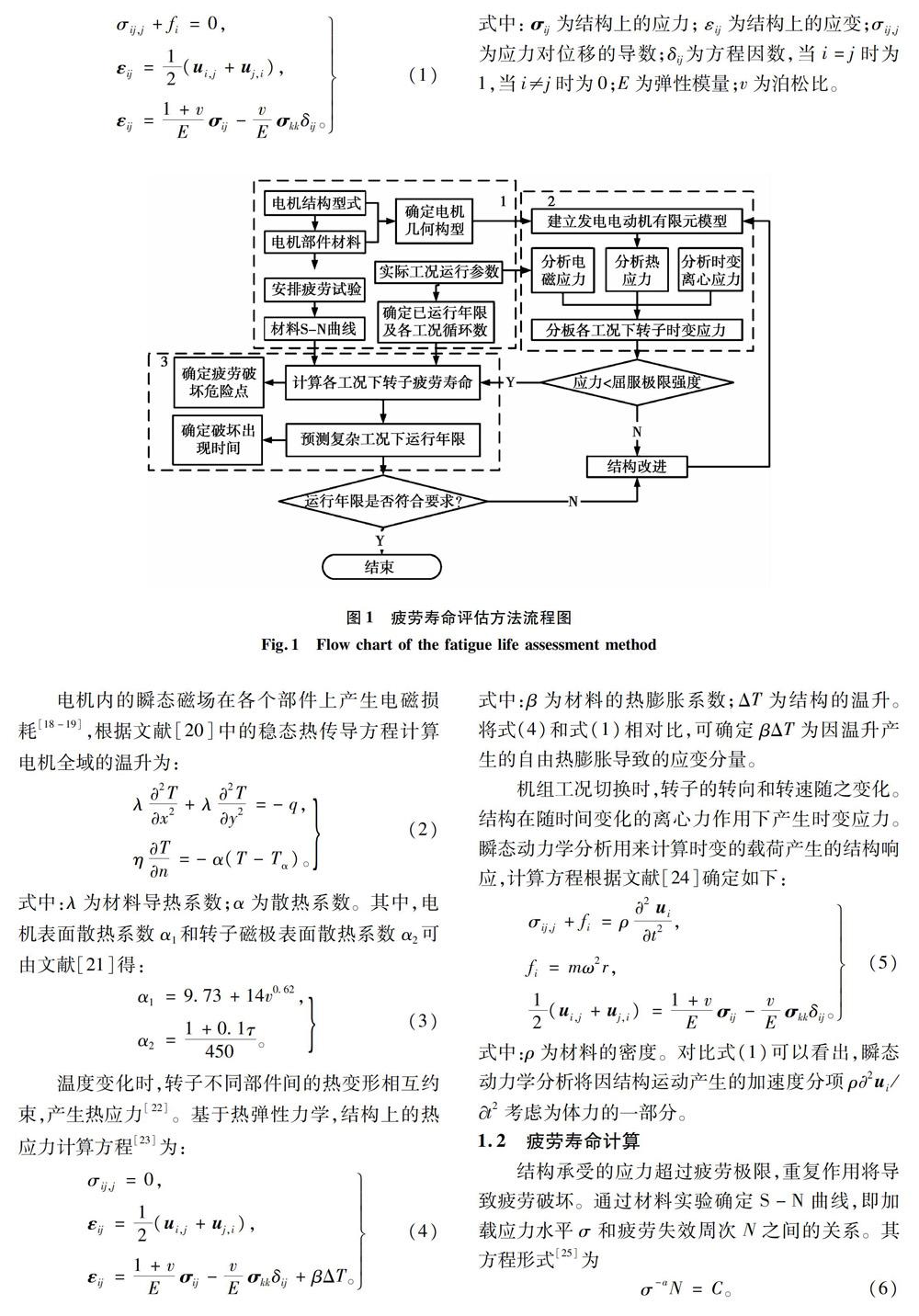
评估发电电动机转子运行年限的前提是正确分析发电启停、电动启停、甩负荷和飞逸工况下结构上的交变应力，并考虑各工况下结构上的疲劳损伤对运行年限缩减的累积效应。这是一个涉及到电磁学、传热学、结构动力学、材料学和疲劳破坏的多学科领域交叉的问题，具体流程如图1所示。

首先，建立发电电动机周期性有限元分析模型。随后，由磁一结构计算求取电磁应力;并提取电机全域的电磁损耗作为热一结构计算的热源，分析电机全域温度分布和转子上的热应力;提取机组实际运行曲线，采用时域动力学分析计算各工况时变离心应力。叠加上述3类应力，分析各种运行情况下转子结构的动态应力。对于超过材料屈服极限的部件，改进其结构从而预防破坏。

选取转子部件实际材料进行实验，确定反映循环应力幅和循环周次的函数关系的S—N曲线。结合已求得的时变应力曲线，确定转子上破坏危险点的位置并计算各工况的最小循环周次。考虑复杂工况对结构剩余寿命的累积影响，结合疲劳损伤准则预测转子的运行年限。最后，根据已确定的破坏危险点位置和破坏出现年限，为机组的检修周期安排提供理论依据。

1.1结构应力分析

电机内的瞬态磁场和转子上的电流相互拉扯产生电磁力。为了简化计算，选取稳态电磁力分析其导致的应力，应力计算的张量方程为：

2模型和参数

本节中，选择一台中国南方电网广州抽水蓄能电站的发电电动机，建立有限元模型。选取转子各部件材料进行实验，确定力学性能和S-N曲线。

2.1模型

忽略端部效应，电机具有很明显的轴向对称性。故选取二维模型分析转子时变应力。从图2可以看出，二维模型具有明显的旋转对称性。为简化计算，选取1/12模型作为分析对象。表1为电机的结构参数和运行参数。磁极和磁轭通过T尾部直接相连，该部位直接限制磁极的离心运动，是电机高速运转时出现峰值离心力的区域。其中，转子磁极材料为500TG硅钢;转子磁轭材料为SD320硅钢。

2.2疲劳实验

本文选取的机组转子各部件的力学性能参数由电测法试验测得，试验对象主要包括：磁轭材料一SD320硅钢;磁极材料-500TG硅钢。同时，安排材料拉伸試验测得了各部件的屈服强度和抗拉强度。具体参数如表2所示。

为获取转子各部件材料的疲劳性能参数，选取磁极、磁轭的备片经加工处理成图3（b）所示的疲劳试样。利用图3（a）所示的RUMUL高频疲劳试验样机。在室温条件下加载频率为110Hz左右的对称拉压应力幅（R=-1），进行高周疲劳试验。建立应力幅σR和循环次数Ⅳ问的关系（S-N曲线），如图3所示。其中，500TG硅钢的疲劳极限为300MPa;SD320硅钢的疲劳极限为315MPa。

3转子结构动应力分析

本节中计算了转子上由电磁力、温升和时变离心力叠加作用的动应力。具体计算内容为：1）电磁力导致的应力根据磁一结构耦合场计算可得;2）提取电磁损耗分析电机的温升，并由热一结构耦合场计算计算热应力;3）根据机组实际转速变化曲线，利用结构动力学计算结构上的时变离心应力。

3.1磁一结构分析

选取二维模型计算转子的电磁力时，将端部效应用集中参数的方法计入电路方程中。采用场路耦合法设定外电路，在定子绕组上加载电压激励。其等效电路和电路参数的计算方程可参照文献[29]。根据表1中的运行参数，计算端部绕组电阻为0.0013Ω，漏感为4.2908uH。负载电阻为0.87Ω，电感为0.0013uH。外电路电压的有效值为14.695kV。

图4所示为机组2种工况下定子电流波形，其中，发电工况相电流峰值为15.48kA，电动工况相电流峰值为15.88kA。根据表1提供的运行参数，由解析法计算实际情况下定子电流的峰值，其中，发电工况相电流峰值为15.15kA，电动工况为15.75kA。对比仿真计算结果，发电和电动工况下的相对误差分别为2.13%和0.82%。

图5为发电和电动2种工况下转子上电磁力波形图。由图可见，电动工况下的最大电磁力为13.5MN，高于发电工况下13.0MN的最大电磁力。提取电动工况下转子上的电磁力，分析其在转子结构上导致的应力。图6为电磁力单独作用下结构的应力分布图，转子最大应力出现在磁轭T尾槽，达到2.12MPa。

3.2热一结构分析

由于发电电动机发电与电动启、停过程不超过5min，且发生甩负荷或飞逸情况时间通常为十几秒。热应力是由于温度变化引起的，根据实际运行监测数据，在启动的短时过程中，温升几乎为0，因此在启动工况下可以忽略热应力的影响。此外，根据运行统计数据，甩负荷与飞逸工况基本都是在稳定运行情况下突然发生的，与停机过程相同，此时的温度仍然是稳定运行工况下的温度值，而转子的热应力也依然由前一个过程的温升引起。综合上述原因，本文在考虑热应力时，采用的是稳态温度场计算方法。通常机组实际运行负荷常低于滿负荷，所以根据实际负荷计算电磁损耗作为温度场的热源。根据实际散热条件，由式（4）计算定子铁心表面和转子磁极表面的等效导热系数。环境温度设定为28℃。

图7所示为电机温度分布云图。其中，根据图7（b）可以看出磁极的温度分布沿着径向递增，在磁极外径出现转子峰值温度，达到71.2℃。考虑到转子热形变沿半径方向不受约束，不会出现热应力集中。结合图7（c）给出的磁轭温度分布可以看出，转子T尾部的峰值温度出现在磁轭T尾槽的T1点和T2点，达到68.4℃。上述2个区域的热形变被磁极T尾所约束，会导致T尾部的热应力过大。

图8为安装在定子铁心中部的机组温度检测系统示意图。由监测系统测得的机组实际运行温度变化区间为61.72℃到64.81℃，取其平均值为63.27℃。对比图7（a）中的定子铁心温度分布，测温点的温度仿真结果约为65.3℃，与实际温度情况相对比的误差仅为3.2%。

图9为转子热应力的分布情况。对比图9（a）和图9（b）中的应力分布情况可以得出，最大热应力出现在磁极T尾部，达到195MPa。而转子除T尾部外的热应力较小，仅为20MPa。并且，T尾部处出现的最大热应力小于材料的屈服强度，结构不会因温度变化出现破坏。

3.3时变离心应力分析

根据广州蓄能电站某机组的实际运行曲线，模拟转子发电模式启停工况、电动模式启停工况、甩负荷工况和飞逸工况的转速变化。各工况转子转速变化曲线如图10所示。

图11为发电工况下结构仅受离心力作用的应力分布情况。峰值应力出现磁轭顺时针方向第5个T尾槽，达到416MPa。对比图6（b）中由电磁力导致的最大应力结果，其仅占到离心力导致应力的0.48%。对比图9中的热应力计算结果，热应力占到离心力导致应力的41.4%。计算转子上的动态应力时，忽略电磁力的影响，同时根据3.2节中的分析，仅在停机、甩负荷及飞逸工况下叠加热应力和离心力导致的应力。

图12为不同工况下转子应力分布情况图。其中，发电工况下的最大应力出现在5号T尾部B点处，这是因为机组做发电机运行时转子为顺时针旋转。而做电动机运行时转子为逆时针旋转，使得其结构的最大应力点出现在1号T尾A点。这将导致发电及电动2种工况下结构出现最大疲劳损伤的位置不同，分析复杂工况下转子疲劳寿命时需要分别针对A点和B点分别考虑。

对比图12和图11中的应力数值可以看出，结构承受离心力作用时的最大应力值为416MPa。然而，计及热应力的影响后，结构上的最大应力上升到466MPa。可以得出，正常运行下的结构应力大于由温度或离心力单独作用的应力。对于采取T尾部连接的转子，机组剧烈的温度变化和工况切换时频繁变化的离心力都将加剧结构的疲劳损伤。

图13是转子在发电模式启动、停机和电动模式下启动、停机，以及甩负荷、飞逸工况下的时变应力曲线。在甩负荷工况下，经过6s转子的叠加应力从466MPa变化到495MPa;在飞逸工况下，经过5s转子的叠加应力从466MPa变化到585MPa。可以看出机组在不同工况切换时，转子上应力会发生明显的变化。在甩负荷和飞逸工况下，结构的峰值应力都不超过材料的屈服极限，因此结构不会发生静力学破坏。由于发电电动机在多种工况下的频繁切换，应力循环超过疲劳极限导致结构疲劳损伤，最终造成转子寿命减短。

4运行年限预测

图12表明不同工况下结构出现最大应力的位置不同，分别出现在转子1号T尾A点和5号T尾B点。计及复杂工况运行下的累积损伤，这2点为最易出现疲劳破坏的位置。本节中，根据图13中的4点和B点2个位置的时变应力曲线和图3中的材料s-N曲线，分别计算各工况下A点和B点最小循环周次。结合实际运行年限下各工况已发生次数，分别预测A点和B点的运行年限，确定最短年限即为结构的剩余寿命。

表3为机组已投运13年内各工况的已发生次数。根据式（8）和式（9）计算4点裂纹形成阶段的累积损伤因子为0.255，裂纹扩展阶段的累积损伤因子为1.89。根据式（10）预测4点的运行年限为57.6年。同样的，可预测B点的运行年限为47.4年。对比机组50年的设计运行年限，其中，B点的预测结果相对误差为5.2%。然而，A点的运行年限结果明显高于设计年限，这是因为，电机设计时基于静力学结果评估寿命强度难以计及复杂工况下结构上的动态应力变化以及各工况累积效应对寿命的影响。从图13可以看出，A点出现最大应力的工况仅为电动模式启停机，而B点出现最大应力的工况为发电模式启停机、甩负荷和飞逸。复杂工况运行时，A点的结构损伤小于B点，而电机设计运行年限时并未考虑因工况变化导致的不同位置的损伤。因此，准确计算各工况下转子结构上的动态应力分布，并考虑复杂工况下累积损伤对寿命的影响，分析各工况下出现最大应力位置的疲劳寿命，可以更好的预测发电电动机复杂工况运行情况下的年限。

5结论

本文针对抽水蓄能发电电动机复杂运行情况下频繁变化的时变应力和累积损伤对转子疲劳寿命的影响，提出动载荷作用下的转子T尾部运行年限预测方法，评估了一台实际运行于广州蓄能电站的机组的运行年限。得到以下主要结论：

1）与传统水轮发电机相比，发电电动机转子结构更易因动载荷作用的疲劳损伤累积导致破坏。常规强度校核法和破坏次数评估法无法准确评估动载荷作用的疲劳损伤对转子寿命的累积影响，本文提出的动载荷作用下转子T尾部疲劳寿命评估方法对预防蓄能机组的疲劳破坏具有工程实际意义。

2）结合多物理场耦合分析和结构动力学计算研究机组运行过程中电磁力、温度和时变离心力在转子结构上叠加导致的时变应力发现，电磁应力远小于其他两项的影响，因此可忽略不计。

3）T尾结构的疲劳破坏危险点位于1号和5号T尾的45°倒角处，在制定检修工作计划时应重点关注该部位。此外，对于电机制造厂家，可重点关注倒角处的设计，改进倒角结构以提高产品的使用寿命。