基于改进的迁移率模型的生物地理学优化算法

王雅萍 张正军 颜子寒 金亚洲

摘 要：生物地理学优化（BBO）算法通过迁移和变异不断更新栖息地，以寻找最优解，其中迁移率模型的优劣会直接影响算法的优化性能。针对原始BBO算法采用线性迁移率模型适应性不足的问题，基于Logistic函数、三次多项式函数以及双曲正切函数提出了三种新的非线性迁移率模型，并应用于原始BBO算法中。对17个典型的基准函数进行优化性能测试，结果表明，基于雙曲正切函数的迁移率模型所得解更接近函数的全局最小值，总体表现优于原始线性迁移率模型的BBO算法以及相关改进算法中表现优异的余弦迁移率模型。稳定性测试结果表明，在不同的变异率下，基于双曲正切函数的迁移率模型在多数测试函数上表现优于原始线性迁移率模型。在满足解多样性的基础上，该模型能够较好地适应非线性迁移问题，提高寻优能力。

关键词：生物地理学优化;迁移率模型;逻辑回归函数;三次多项式;双曲正切函数

中图分类号：TP301.6

文献标志码：A

Biogeography-based optimization algorithms based on improved migration rate models

WANG Yaping， ZHANG Zhengjun*， YAN Zihan， JIN Yazhou

School of Science， Nanjing University of Science and Technology， Nanjing Jiangsu 210094， China

Abstract：

Biogeography-Based Optimization （BBO） algorithm updates habitats through migration and mutation continuously to find the optimal solution， and the migration model affects the performance of the algorithm significantly. In view of the problem of insufficient adaptability of the linear migration model used in the original BBO algorithm， three nonlinear migration models were proposed. These models are based on Logistic function， cubic polynomial function and hyperbolic tangent function respectively. Optimization experiments were carried out on 17 typical benchmark functions， and results show that the migration model based on hyperbolic tangent function performs better than the linear migration model of original BBO algorithm and cosine migration model with good performance of improved algorithm. Stability test shows that the migration model based on hyperbolic tangent function performs better than the original linear migration model with different mutation rates on most test functions. The model satisfies the diversity of the solutions， and better adapts to the nonlinear migration problem with improved search ability.

Key words：

Biogeography-Based Optimization （BBO）; migration rate model; logistic regression function; cubic polynomial; hyperbolic tangent function

0 引言

受生物地理学[1-5]启发，Simon[6]于2008年提出了生物地理学优化（Biogeography-Based Optimization， BBO）算法。BBO算法中的主要操作为迁移和变异。根据物种中每个个体的适应度函数，通过迁移和变异寻找全局最小值点。Simon在最初的BBO算法中采用线性迁移率模型，并实证证明与其他基于物种的优化算法相比，BBO在多数特定测试函数上表现更好，具有一定的实际应用价值。

马海平等[7]根据生物地理学物种分布情况，提出了指数迁移率模型、二次迁移率模型和余弦迁移率模型，在8个基准函数上进行测试分析;Ma[8]还提出了常数与线性混合迁移率模型和梯形迁移率模型[8]。Simon[9]提出了简化版的BBO算法，并且利用概率论分析其优化性能。吴斌等[10]提出了三种迁移操作模式，实验结果表明迁入主导的部分迁移式算子优化性能最佳。Feng等[11]在更新栖息地的过程中引入了随机栖息地，进而丰富物种多样性。Farswan等[12]在更新栖息地的过程中引入了迁入栖息地、随机栖息地，增加了解的多样性;他们还引入最佳栖息地，进一步修正更新规则[13]。Guo等[14]提出均匀混合迁移算子、启发式迁移算子以及拓展式迁移算子，提高了基本BBO算法的探索能力。唐继勇等[15]提出了一种基于动态选择迁出地与混合自适应迁入的优化策略，提高了全局搜索能力。

本文介绍了BBO算法，并针对BBO算法中线性迁移率模型适应性不足的问题，分别基于Logistic函数、三次多项式以及双曲正切函数提出了三种非线性迁移率模型应用于BBO算法的迁移操作。实证表明，基于双曲正切函数迁移率模型的BBO算法在多数测试函数下表现最佳，其解更接近函数的全局最小值。

1 生物地理学优化算法

1.1 生物地理学

生物地理学由自然学家Alfred Wallace和Charles Darwin于19世纪提出，其数学模型描述了物种在栖息地之间的迁移、新物种的产生以及物种的灭绝。栖息地适宜度指数（Habitat Suitability Index， HSI）用以衡量栖息地适合物种生存的程度，该值越大则越适宜物种生存。HSI由许多因素构成，包括气温、降水、植被的多样性以及土地面积等。这些影响HIS的因素称为适宜度指数变量（Suitability Index Variable， SIV）。由于栖息地的资源有限，通常适宜度高的栖息地趋向于容纳较多物种，且本地物种有较大的可能性迁出到其他栖息地，同时外来物种的迁入率较低;而适宜度低的栖息地趋向于包含较少的物种，且外来物种有较大的可能性迁入本地，同时迁出的可能性较小。此外，自然灾害等大变动事件也可能会改变栖息地的状态，进而影响HSI。

为了形式化地描述BBO模型，假设某栖息地容纳物种数量为S的概率为Ps。则由Ps在t时刻的取值，可得其在（t+Δt）时刻的取值：

Ps（t+Δt）=Ps（t）（1-λsΔt-μsΔt）+Ps-1（t）λs-1Δt+Ps+1（t）λs+1Δt（1）

其中：λs和μs分别为当前栖息地物种数量为S时的迁入率和迁出率。式（1）是考虑以下三种情况所得的：

1）当前栖息地在t时刻的物种数量为S，并且在接下去的Δt时间内不发生迁移。

2）当前栖息地在t时刻的物种数量为S-1，并且在接下去的Δt时间内有一个物种迁入。

3）当前栖息地在t时刻的物种数量为S+1，并且在接下去的Δt时间内有一个物种迁出。

当Δt足够小时，期间发生超过一次迁移的概率几乎为0。令P=[P0，P1，…，Pn]T，n=Smax ，由此可得式（1）的极限形式：

=AP（2）

1.2 生物地理学优化算法

基于以上生物地理学理论，通过迁移和变异不断更新栖息地的適应度，构成了生物地理学优化算法。迁移步骤如算法1所示。

算法1 BBO算法中的迁移步骤。

程序前

以正比于λi的概率选择迁入栖息地Hi

If Hi被选择

For每个栖息地

以正比于μi的概率选择迁出栖息地Hj

If Hj被选择

从Hj中随机选择迁出SIV σ

将Hi中随机选取的SIV替换为σ

End

End

End

程序后

变异步骤如算法2所示。

算法2 BBO算法中的变异步骤。

程序前

对于栖息地Hi

For 每个SIV

根据λi和μi计算变异概率Pi

以正比于Pi的概率选择变异SIV为Hi（j）

If Hi（j）被选择

将Hi（j）替换为随机产生的SIV

End

End

程序后

BBO算法流程如算法3所示。

算法3 BBO算法。

程序前

初始化物种数量、迁移率、变异率以及精英数。

计算各栖息地的HSI

While 停止条件未满足 do

将各栖息地按照HIS从高到低进行排序

利用算法1进行迁移操作

更新各栖息地的HIS

利用算法2进行变异操作

保持当前迭代所有栖息地中的精英

End while

程序后

2 迁移率模型

Simon采用线性模型来模拟自然界中物种迁移的规律，即认为随着物种数量的增加，迁入率呈线性递减趋势，同时迁出率呈线性递增趋势。在相关改进算法中，Ma等[7]提出的余弦迁移率模型在其测试的多数函数下表现最佳，认为接近自然规律的迁移率模型优于简单的线性模型。

为了更好地适应非线性迁移问题，本文提出三种不同变化趋势的非线性迁移率模型，并与原始线性模型以及相关改进算法中表现优异的余弦迁移率模型[7]进行对比分析。如图1所示，在最大迁入率I和最大迁出率E下，迁入率λk和迁出率μk是关于物种数量k的函数，k0为迁入率等于迁出率的平衡点。

模型1 原始线性模型。

线性模型的迁入率和迁出率如下：

λk=I（1-k/n）

μk=E（k/n）（9）

如图1（a）所示，在线性迁移率模型下，随着物种数量的增加，迁入率从I开始线性下降至0，同时迁出率从0开始线性上升至E。

模型2 余弦模型。

余弦模型[7]的迁入率和迁出率如下。

λk=I2coskπn+1

μk=E2-coskπn+1（10）

如图1（b）所示，在余弦迁移率模型下，当物种数量较多或较少时，迁移率变化比较平稳;当具有一定物种数量时，迁移率相对变化较快。

模型3 Logistic模型。

Logistic模型的迁入率和迁出率如下：

λk=I1-11+en2-k

μk=E1+en2-k（11）

如图1（c）所示，在Logistic迁移率模型下，当物种数量较多或较少时，迁移率变化非常平稳;当具有一定物种数量时，迁移率变化很快。

模型4 三次多项式模型。

三次多项式模型的迁入率和迁出率如下：

λk=I2-（2k-n）3n3+1

μk=E2（2k-n）3n3+1（12）

如图1（d）所示，在三次多项式迁移率模型下，在物种数量较多或较少时，迁移率变化较快;而具有一定物种数量时，迁移率变化趋于平缓。

模型5 双曲正切变型模型。

双曲正切变型模型的迁入率和迁出率如下。

λk=I2-ak-n2-a-k+n2ak-n2+a-k+n2+1

μk=E2ak-n2-a-k+n2ak-n2+a-k+n2+1（13）

如图1（e）所示，在双曲正切变型迁移率模型（本文取a=1.1）下，迁移率随物种数量变化的趋势类似于余弦模型，但是幅度比余弦模型更缓和些。

3 实证分析

在python3.6的环境下，针对17个典型的基准函数，分别利用提出的三种基于非线性迁移率模型的BBO算法进行测试，并与原始线性迁移率模型以及相关改进算法中表现优异的余弦迁移率模型[7]进行对比分析。基准函数信息如下所示。

1）Sphere：

f1（x）=∑Di=1xi2; -10≤xi≤10， D=20

2）Schwefel221：

f2（x）=maxxi; 1≤i≤D， -10≤xi≤10， D=20

3）Griewank：

f3（x）=∑Di=1xi24000-∏Di=1cos（xi/i）+1;

-600≤xi≤600， D=20

4）Axis parallel hyper ellipsoid：

f4（x）=∑Di=1ixi2; -5.12≤xi≤5.12， D=20

5）Alpine：

f5（x）=∑Di=1xi sin xi+0.1xi; -10≤xi≤10， D=20

6）Exponential：

f6（x）=-exp（-0.5∑Di=1xi2）; -1≤xi≤1， D=20

7）Cosine mixture：

f7（x）=∑Di=1xi2-0.1∑Di=1cos（5πxi）; -1≤xi≤1，D=20

8）Zakharov function：

f8（x）=∑Di=1xi2+（∑Di=10.5ixi）2+（∑Di=10.5ixi）4;

-5≤xi≤10， D=20

9）De jongs：

f9（x）=∑Di=1ixi4; -5.12≤xi≤5.12， D=20

10）Michalewicz：

f10（x）=-∑Di=1sin（xi）sin2m（ix2i/π）; 0≤xi≤π， D=10

11）Easom：

f11（x）=-cos（x1）cos（x2）e-（x1-π）2-（x2-π）2，

-100≤xi≤100， D=2

12）Ackley：

f12（x）=-20 exp（-0.21D∑Di=1x2i）-

exp（1D∑Di=1cos（2πxi））+20+e; -30≤xi≤30， D=20

13）Schwefel222：

f13（x）=∑Di=1xi+∏Di=1xi; -10≤xi≤10， D=20

14）Step function

f14（x）=∑Di=1（xi+0.5」）2; -100≤xi≤100， D=20

15）Schwefel：

f15（x）=418.9829D-∑Di=1xi sin（xi12）;-500≤xi≤500， D=20

16）Rastrigin：

f16（x）=10D+∑Di=1[xi2-10 cos（2πxi）];-5.12≤xi≤5.12， D=20

17）Salomon prol 3：

f17（x）=1-cos（2π∑Di=1xi2）+0.1∑Di=1xi2;-100≤xi≤100， D=20

所有測试函数有且仅有一个全局最小值点，其中f3、 f5、 f7、 f12、 f15和f16有许多局部极小值点，优化算法在寻找最优解时容易陷入局部极小值点而无法达到全局最小值点。

f10的全局最小值为-9.66015， f6和f11的全局最小值为-1， f7的全局最小值为-2，其余函数全局最小值均为0。

3.1 迁移率模型优化性能分析

为了平行比较基于不同迁移率模型的BBO算法的性能，有关参数设置如下：

最大迁移率I=E=1，物种（栖息地）数量PopSize=30，迭代次数Iteration=50，变异率m=0.01。

为了降低算法中随机因素的影响，各模型独立运行50次，观察平均值和最小值。5种模型测试结果的平均值如表1所示。

由表1可知，从平均值的角度来看，不同迁移率模型优化性能差别很大。总体来说，模型5在大多测试函数上表现最佳，模型2其次，而模型4表现差强人意，仅在3个测试函数上优于模型1。

17个函数在不同迁移率模型下求解的平均最小值误差百分比变化趋势如图2所示。

由圖2可知，就平均最小值误差百分比而言，对于多数测试函数来说，模型4的误差百分比最大，而模型2和模型5长期处于较低的误差水平。在不考虑模型4的情况下，函数f5、 f6、 f8、 f9和f17受迁移率模型影响较大，其余函数受迁移率模型影响相对较小。

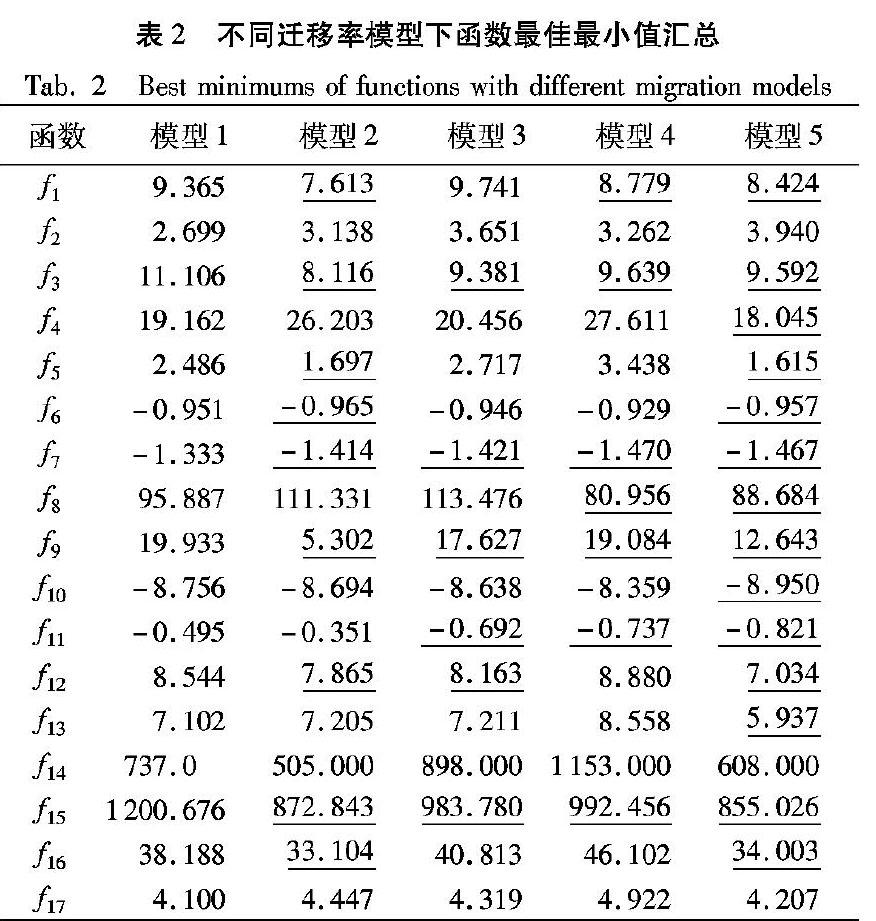
5种模型测试结果的最佳最小值如表2所示。

由表2可知，从最小值的角度来看，模型5的表现仍然优异，并且模型4的优化性能有所提升，而模型2的寻优能力有所降低。

17个函数在不同迁移率模型下求解的最佳最小值误差百分比变化趋势如图3所示。

由图3可知，就最佳最小值误差百分比而言，BBO算法寻找函数最小值时受迁移率模型影响很大。模型5的总体表现最稳定，在14个测试函数上误差小于模型1，并且长期处于低误差水平。模型2的性能有所下降，仅在9个测试函数上误差小于模型1。

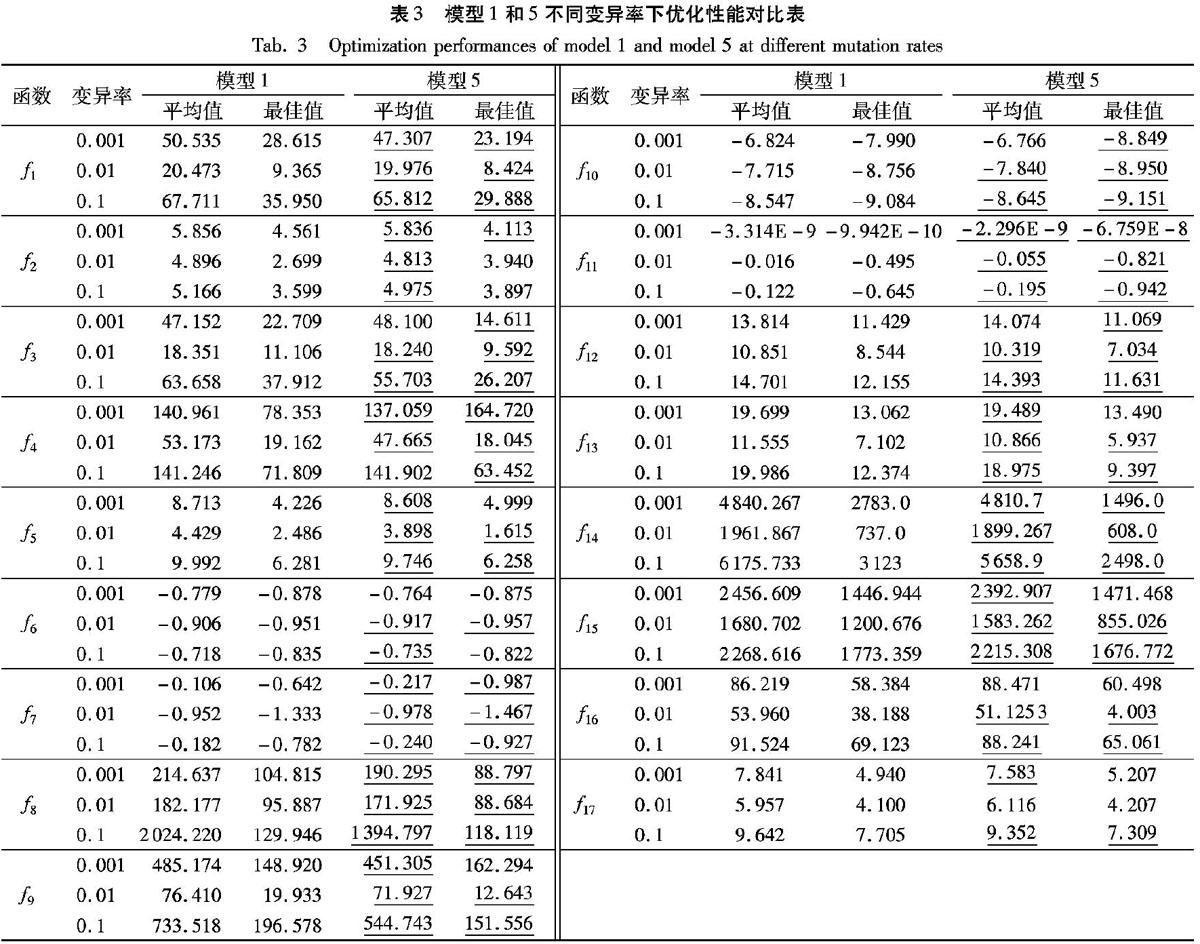
3.2 稳定性分析

改变物种最大变异率可以调节解的多样性。为了研究不同

迁移率模型的稳定性，对比分析原始线性模型（模型1）和本文所

提最佳模型（模型5）在不同迁移率下的表现，如表3所示。

由表3可知，不同变异率下所得平均值和最小值变化不一， f7、 f8、 f9受变异率的影响较大，其余函数受影响较小。总体上变异率为0.01时模型性能最佳，并且在多数测试函数上模型5的表现优于模型1。

4 结语

生物地理学优化算法性能受其迁移率模型影响显著。本文提出三种新的非线性迁移率模型，并应用于17个典型的基准函数求最小值问题。结果显示，在多数测试函数下，基于双曲正切变体迁移率模型的BBO算法寻优能力最佳，其解更接近函数的全局最小值。变异率作为影响BBO算法优化性能的另一重要因素，有待进一步研究。

参考文献

[1]WALLACE A R. The geographical distribution of animals [J]. Nature， 1958， 182（4629）： 140-141.

[2]DARWIN C. The Origin of Species [M]. New York： Bantam Classics， 1995： 218-230.

[3]HANSKI I， GILPIN M E. Metapopulation Biology [M]. New York： Academic Press， 1997： 63-67.

[4]XING B， GAO W-J. Biogeography-based optimization algorithm [M]// Innovative Computational Intelligence： A Rough Guide to 134 Clever Algorithms， LSRL 62. Berlin： Springer， 2014： 81-91.

[5]GUO W， WANG L， WU Q. Numerical comparisons of migration models for multi-objective-biogeography-based optimization [J]. Information Sciences， 2016， 328（C）： 302-320.

[6]SIMON D. Biogeography-based optimization [J]. IEEE Transactions on Evolutionary Computation， 2008， 12（6）： 702-713.

[7]马海平，李雪，林升东.生物地理学优化算法的迁移率模型分析[J].东南大学学报（自然科学版），2009，39（S1）：16-21.（MA H P， LI X， LIN S D. Analysis of migration rate models for biogeography-based optimization [J]. Journal of Southeast University （Natural Science Edition）， 2009， 39（S1）： 16-21.）

[8]MA H. An analysis of the equilibrium of migration models for biogeography-based optimization [J]. Information Sciences—Informatics and Computer Science， Intelligent Systems， Applications： An International Journal， 2010， 180（18）： 3444-3464.

[9]SIMON D. A probabilistic analysis of a simplified biogeography-based optimization algorithm [J]. Evolutionary Computation， 2011， 19（2）： 167-188.

[10]吴斌，林锦国，崔志勇.生物地理学优化算法中迁移算子的比较[J].计算机工程与应用，2012，48（25）：61-64.（WU B， LIN J G， CUI Z Y. Compative study of migration operators in biogeography optimization [J]. Computer Engineering and Applications， 2012， 48（25）： 61-64.）

[11]FENG Q， LIU S， ZHANG J， et al. Biogeography-based optimization with improved migration operator and self-adaptive clear duplicate operator [J]. Applied Intelligence， 2014， 41（2）： 563-581.

[12]FSRSWAN P， BANSAL J C. Migration in biogeography-based optimization [C]// Proceedings of the 4th International Conference on Soft Computing for Problem Solving， AISC 336. Berlin： Springer， 2014： 389-401.

[13]FARSWAN P， BANSAL J C， DEEP K. A modified biogeography based optimization [M]// Harmony Search Algorithm， AISC 382. Berlin： Springer， 2016： 227-238.

[14]GUO W， WANG L， SI C， et al. Novel migration operators of biogeography-based optimization and Markov analysis [J]. Soft Computing， 2016， 21（22）： 6605-6632.

[15]唐繼勇，仲元昌，曾广朴.基于迁出地动态选择与自适应迁入策略的BBO算法[J].计算机科学，2016，43（10）：282-286.（TANG J Y， ZHONG Y C， ZENG G P. Biogeography-based optimization with adaptive immigration and dynamic selection emigration strategy [J]. Computer Science， 2016， 43（10）： 282-286.）

This work is partially supported by the National Natural Science Foundation of China （61773014）.

WANG Yaping， born in 1995， M. S. candidate. Her research interests include data mining.

ZHANG Zhengjun， born in 1965， Ph. D.， associate professor. His research interests include data mining， graphics and images.

YAN Zihan， born in 1995， M. S. candidate. Her research interests include data mining.

JIN Yazhou， born in 1993， M. S. candidate. His research interests include data mining.