基于PCA的高校学生专业技术能力评价模型

毕瑶家 刘国柱 凌明华 黄文

摘要：对高校学生成绩的评价是教育的重要内容，传统的高校学生评价方式大多采用综合素质测评的方式，此方法指标模糊，计算方法不科学，无法真正体现学生的真实情况。根据国家工程认证的思想以及高校学生的现状，提出了新的学生专业技术能力评价指标体系以及基于主成分分析的高校学生专业技术能力评价模型，主成分分析法的优点是各主成分的权数为其贡献率，它反映了该主成分包含原始数据的信息量占全部信息量的比重，这样确定权数是客观的、合理的，它克服了某些评价方法中认为确定权数的缺陷。该模型能够更加准确、全面地对学生的课程成绩进行评价，将该评价模型的结果与学生毕业后的情况进行对比，结果表明，该评价模型能够在一定程度上反映学生的专业技术能力。

关键词：高校学生;专业技术能力;教育评价;主成分分析法

中图分类号：G642      文献标识码：A

文章编号：1009-3044（2019）22-0117-02

开放科学（资源服务）标识码（OSID）：

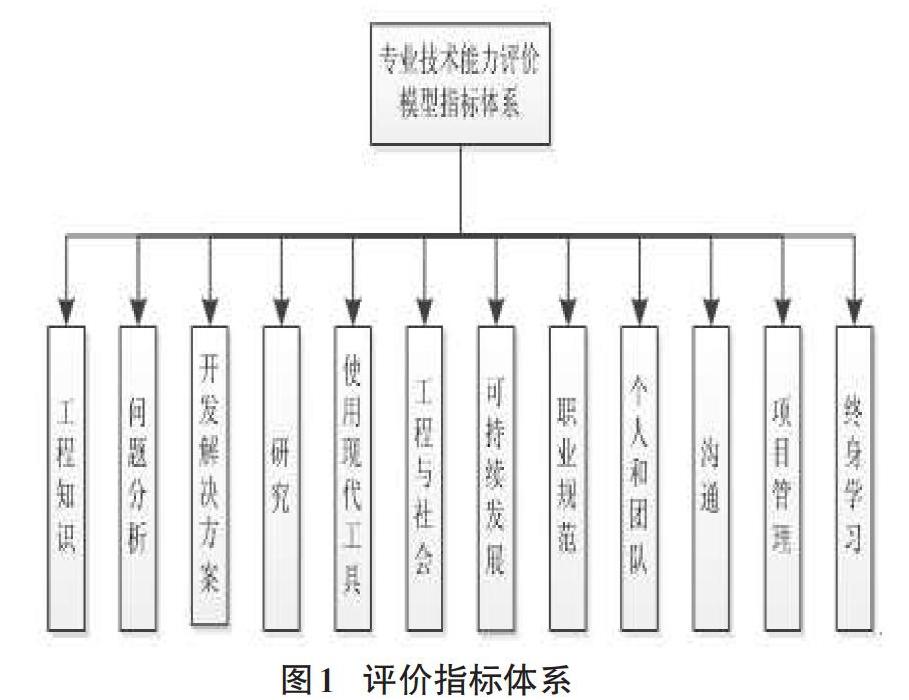
1 评价指标体系的建立

本文以青岛科技大学软件工程专业毕业生为例，从科学评价的角度出发，采用问卷调查法、个别访谈法、集体访谈法等方法，结合专业认证专家的评审意见和现有文献进行指标的海，遴选出十二个与学生专业技术能力相关的指标点，如表1所示。

根据合理性、公平性和科学性的评价原则，最终在十二个一级指标点的基础上建立47个二级指标点。二级指标的权重配置相对简洁明了，故本体系在二级指标权重配置中采用经验确定法。即实践经验丰富的学者专家，根据他们长期的工作经验和主观认识，共同商议而确定二级指标各项权数，以工程知识为例，其指标体系的建立如表1所示：

2 PCA评价模型的建立及改进

本文采用主成分分析法来评价高校学生的专业技术能力。主成分分析法是将原来众多的具有一定相关性的能力评价指标重组成一组相互无关的、新的综合指标来代替原指标，新的在综合指标保留了原指标的最主要特征。并根据实际的需要从这些指标中抽取几个较少的综合变量来尽量多的反应原变量的信息。

（1） 对原始数据进行标准化处理.假设参与评价的人数为[n]人，每一个评测对象有12个能力评价指标，我们就可以用原始数据构造一个[n×12]维的矩阵，表示为[（Xij）n×12]，其中[i=1，2，3，…]。将各个指标值[Xij]转化成标准化指标[Xij]。

（2） 求出矩阵[Xij]的相关系数矩阵[R]的特征值[λii=1，2，…，p]且[λ1≥λ2≥…≥λp≥0]。以及对应的特征向量[u1，u2，…，um]，其中[uj=（u1j，u2j，…，umj）T]，由特征向量组成[m]个，新的指标变量。

[y1=u11x1+u21x2+…+um1xmy2=u12x1+u22x2+…+um2xm………………………………ym=u1mx1+u2mx2+…+ummxm]式中[y1]是第1主成分，[y2]是第2主成分，[...]，[ym]是第[m]主成分。

（3） 选择[p]个主成分，计算综合评价值。计算特征值的信息贡献率和累计贡献率。称为主成分[yj]的信息贡献率，表示为[αp]。当[αp]接近于1时，选择[p]个主成分代替原来[m]个指标，然后综合分析[p]个主成分。并且可以计算每一个主成分的综合得分：

[Z=j=1pbjyj]

其中[bj]为第[j]个主成分的信息贡献率，根据每一个主成分的综合得分就可以进行评价。

3 实例分析

本文选取了青岛科技大学软件工程专业13级的毕业生为研究对象，共计47名毕业生。每一个测评对象有12个能力指标，构成一个[47×12]的矩阵。首先对原始矩阵进行标准化处理，然后对标准化之后的数据进行.KMO和Bartlett检验。检验结果为.KMO值为0.710，大于0.6;Bartlett球度检验的Sig值为0，小于显著水平0.05.这说明我们提供的指标间存在相关关系，符合因子分析的条件，可以进行因子分析，然后进一步完成主成分分析。表2中给出特征值大于1的主成分。

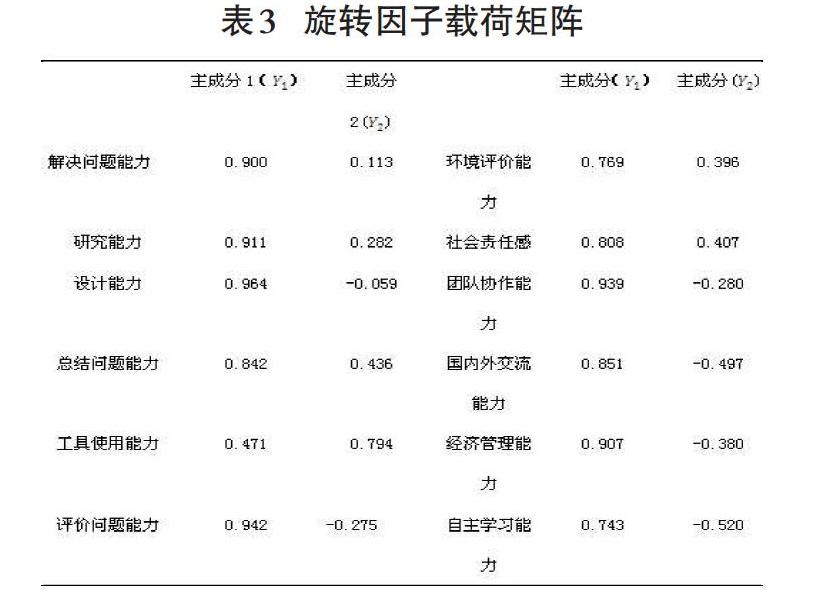
表2显示前2个主成分的特征值大于1且贡献率大于85%，因此选择前两个成分为主要成分。采用方差最大旋转法进行因子正交旋转，得到旋转因子载荷矩阵，见表3。

将载荷因子与其对应的指标初始值的乘积之和作为评价得分，公式如下：

[Y1=0.900×X1+0.911×X2+0.964×X3+0.842×X4+0.471×X5+0.942×X6+0.769×X7+0.808×X8+0.939×X9+0.851×X10+0.907×X11+0.743×X12]

[Y2=0.113×X1+0.282×X2-0.059×X3+0.436×X4+0.794×X5-0.275×X6+0.396×X7+0.407×X8-0.280×X9-0.497×X10-380×X11-0.520×X12]

根据综合评价的得分公式：[Y=b1*Y1+b2*Y2].[b1，b2]为旋转之前的方差贡献率，分别问8.614和2.054.本文将[b1，b2]做归一化处理，得到的权重为[ω1]和[ω2]，分别为8.614/10.668和2.054/10.668，最终的综合评价模型为：

[Y=8.61410.668*Y1+2.05410.668*Y2]

根據综合评价模型，计算学生的专业能力综合评价得分并进行排名，将学生的原始排名与综合评价排名进行对比，将软件工程专业13级学生的专业能力评价排名与常规计算方式得到的成绩排名做了对比，可以发现排名情况差异非常明显。根据调查13级软件工程同学目前工作情况，该模型对同学的专业技术能力评价更加符合实际的情况，因此该模型能够比常规的成绩更加真实地反映出学生的专业技术能力。根据分析，造成差异的主要原因是传统的成绩计算方式采用平均学分绩法即将每门课程的原始分数与该门课程的学分数相乘后求和，再除以课程的总学分。其缺点是不同课程的原始分数缺乏可加性和可比性，存在许多人为主观因素的影响，其计算过程存在信息重叠，难以反映出学生真正的专业技术能力;而采用主成分分析的专业能力评价模型，根据国家工程认证的思想选取了12个指标点对专业技术能力惊醒评价，并通过将多维变量进行综合降维处理，避免了常规计算当中过多的信息重叠，使得到的结果更加的具有科学性和合理性。

4 结论

新的专业能力评价模型是在国家工程认证的思想上提出的，在指标点的选取更加具有科学性，通过主成分分析的综合降维处理，减少了指标信息的重叠，使结果更加具有合理性。根据最终的调研结果，证明新模型的计算结果比传统的成绩计算方式的结果更加符合学生的实际情况。新模型通过SPSS软件即可使用，方便计算，比较直观，其结果具有科学性和合理性，既可以对教学工作做出指导意见，也可以作为学生工作中评奖评优的参考。

参考文献：

[1] 严长远，陈刚. 高校大学生综合素质测评工作评价研究[J].高教与成才研究，2016（8）.

[2] 侯小洁，张俊华. 基于分组主成分分析法的大学生综合素质测评研究[J].赤峰学院学报，2018（8）.

[3] 周露.大学生综合素质测评的问题与改进 ———以三所“985 工程大学”为例[D].长沙：湖南大学，2013.37-38.

[4] 刘譞.基于学生行为的成绩预测模型的研究与应用[D].成都：电子科技大学，2017.

[5] 朱丽琴.基于随机森林算法的学生成缋评价研究[D].安徽：安徽工业大学，2017.

[6] 邹晨红.基于模糊综合评判的大学生综合素质评估模式研究[J].软件导刊，2017（16-17）.

[7] 迟国泰，曹婷婷，张昆.基于相关—主成分分析的人的全面发展评价指标体系构建[J].系统工程理论与实践，2013，32（1）：112-119.

【通联编辑：李雅琪】