遗传计算中数学模型的构建

张玉平 冯明董

（1广东广雅中学 广东广州 510160）

关于基因频率的考题中，常会有这样的情况：已知常染色体隐形基因（a）的频率，需要据此求出显性表现群体（AA 和Aa）中携带者（Aa）的频率。这时常规解法往往需要利用遗传平衡定律,先分别求出AA 和Aa 的频率，然后再求出其中Aa 的频率。这样的算法在计算过程中数据往往比较复杂，有分数和平方，极易出错，许多学生知道怎么做，却由于计算问题，耗费了大量时间，最后得出的却是错误答案。考试时，由于时间紧迫，很大一部分学生看到此类题会直接放弃。

1 规律的发现及数学模型的归纳

在教学过程中，笔者发现此类题的答案有一定的规律，并归纳总结出一定的数学模型，再用数学方法加以证明。有此模型，在已知常染色体隐形基因（a）的频率时，不用再去利用遗传平衡定律进行繁琐的计算，直接将数据套入一个简单的公式，可快速而准确地算出显性表现群体中携带者的频率，极大节约了时间，提高了准确率。

例1，假设群体中某常染色体隐形基因（a）的频率是1／10，则显性表现群体（AA 和Aa）中携带者（Aa）的频率为_______________。

1.1 常规解法 运用遗传平衡定律，首先分别求出总群体中AA 和Aa 的频率，再求出显性表现群体中携带者的频率，如下所示：

2种基因的频率分别为a：1/10；A：9/10。

2种显性表现基因型的频率分别为AA：（9/10）2=81/100；Aa：2×（1/10）×（9/10）=18/100。

所以，显性表现群体中携带者的频率为：

Aa/（AA+Aa）=（18/100）/（18/100+81/100）=2/11。

1.2 总结规律，归纳模型 这类题做多了会发现以下规律：

1）若2种基因的频率分别为a：1／20；A：19／20。

则2种显性表现基因型的频率分别为AA：（19/20）2；Aa：2×（1／20）×（19／20）。

显性表现群体中携带者的频率为：Aa／（AA+Aa）=2／21。2）若2种基因的频率分别为a：1/30；A：29/30。

则2种显性表现基因型的频率分别为AA：（29／30）；Aa：2×（1/30）×（29／30）。

显性表现群体中携带者的频率为：Aa／（AA+Aa）=2／31。

按照以上规律，以此类推，根据数学方法归纳出数学通式，设a 的基因频率为m，则正常群体中携带者的概率=2／（1+1／m）。

2 数学模型的论证

此通式是否具有普遍性，遗传计算中能否大胆放心使用？ 笔者用数学方法加以论证。

若2种基因的频率分别为a：m；A：1-m。

则2种显性表现基因型的频率分别为AA：（1-m）2；Aa：2m（1-m）。

显性表现群体中携带者的频率为：Aa／（AA+Aa）=2m（1-m）／［（1-m）2+2m（1-m）］

=2m／（1+m）

＝2／（1+1/m）。

3 数学模型的应用

例2，（2013年安徽省理综，第31题）图1是一个常染色体遗传病的家系系谱。致病基因（a）是由正常基因（A）序列中一个碱基对的替换而形成的。图2显示的是A 和a 基因区域中某限制酶的酶切位点。分别提取家系中Ⅰ1、Ⅰ2和Ⅱ1的DNA，经过酶切、电泳等步骤，再用特异性探针做分子杂交，结果见图3。

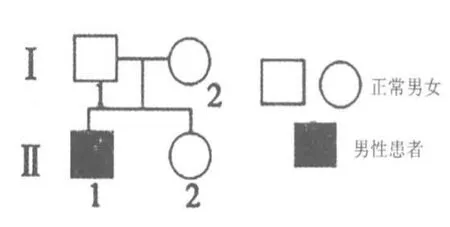
图1

图2

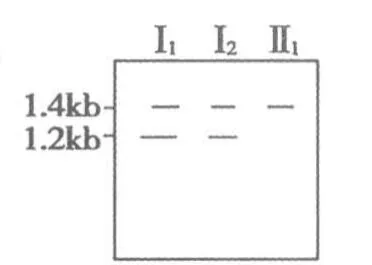
图3

1）Ⅱ2的基因型是________。

2）一个处于平衡状态的群体中a 基因的频率为q。如果Ⅱ2与一个正常男性随机婚配，他们第1个孩子患病的概率为______。如果第1个孩子是患者，他们第2个孩子正常的概率为_______。

3）研究表明，世界不同地区的群体之间，杂合子（Aa）的频率存在着明显的差异。请简要解释这种现象。①_____________；②________________。

4）B 和b 是一对等位基因。为了研究A、a 与B、b 的位置关系，遗传学家对若干基因型为AaBb和AABB 个体婚配的众多后代的基因型进行了分析。结果发现这些后代的基因型只有AaBB 和AABb 2种。据此，可以判断这2对基因位于____染色体上，理由是__________________________。

5）基因工程中限制酶的作用是识别双链DNA分子的____________，并切割DNA 双链。

6）根据图2和图3，可以判断分子杂交所用探针与A 基因结合的位置位于______________。

答案：1）aa 2）q／3（q+1） 3/43）①不同地区基因突变频率因环境的差异而不同 ②不同环境条件下，选择作用会有所不同 4）一对同源个体AaBb 只能产生aB 和Ab 2种配子 5）核苷酸序列6）酶切位点①与②之间。

针对小题2的2种解法比较。

传统解法：①根据图中信息可推知Ⅰ1、Ⅰ2基因型均为Aa，Ⅱ2基因型情况为1／3AA、2／3Aa；②Ⅱ2的丈夫表现正常，其他信息不知，只能从群体中的频率计算其基因型情况，根据题干首先得出A 频率为1-q，再推出AA、Aa 的频率分别为（1-q）2和2q（1-q），Ⅱ2的丈夫表现正常，所以其为携带者的概率为2q（1-q）／［（1-q）2+2q（1-q）］，化简为2／（1+1／q）； ③最后再算出Ⅱ2夫妇生出患病孩子的概率为（2／3）×［2／（1+1／q）］×（1／4）=q/3（q+1）。

应用数学模型法：①据题知Ⅱ2基因型情况为1/3AA、2/3Aa；②丈夫表现正常，其他未知,可利用数学模型快速得知其为携带者的概率为2/（1+1/q）；③Ⅱ2夫妇所生孩子患病概率为（2/3）×[2/（1+1/q）]×（1/4）=q/3（q+1）。

经比较可以发现传统解法中间步骤较多，计算繁琐，容易出错。而利用数学模型法，计算步骤少，更加简单直接，准确率高，还节约时间。

例3，图4为某家族甲、乙2种遗传病（均不威胁生命）的系谱图。甲遗传病由一对等位基因（A、a）控制，且甲病在人群中发病率为1／900；乙遗传病由另一对等位基因（B、b）控制，这2对等位基因独立遗传。已知Ⅲ-4携带甲遗传病的致病基因，但不携带乙遗传病的致病基因。回答问题：

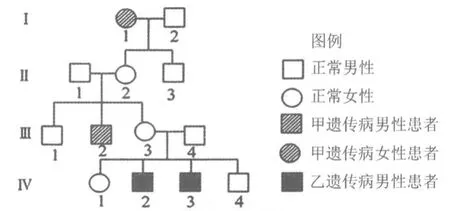
图4

1）甲病的遗传方式是________，乙病的遗传方式是________。

2）Ⅱ-2的基因型为__________，Ⅲ-3的基因型为_________。

3）若Ⅲ-3和Ⅲ-4再生一个孩子，则这个孩子为同时患甲、乙2种遗传病男孩的概率是_______。

4）若Ⅳ-1与一个正常男性结婚，则他们生一个患甲遗传病孩子的概率是______。

答案：1）常染色体隐性遗传 伴X 染色体隐性遗传2）AaXBXbAAXBXb或AaXBXb3）1/244）3／310。

针对小题4的2种解法比较。

传统解法：①根据题干信息可知Ⅲ-3甲病基因型情况为1／3AA，2／3Aa，Ⅲ-4基因型为Aa，而Ⅳ-1表现正常，其基因型情况为2／5AA，3／5Aa；②Ⅳ-1的丈夫表现正常，其他信息不知，只能从群体中的频率计算其基因型情况。根据发病率可知aa 频率为1／900，所以a、A 的频率分别为1／30和29／30，所以AA、Aa 的频率分别为841／900和58／900，所以其为携带者的概率为（58／900）／［（841／900）+（58／900）］=2/31； ③Ⅳ-1夫妇生出患病孩子的概率为（3／5）×（2／31）×（1／4）=3／310。

应用数学模型法：①据题可推知Ⅳ-1甲病基因型情况为2／5AA，3／5Aa； ②丈夫表现正常，其他未知，而人群中发病率为1／900，则a 频率为1／30，可利用数学模型快速得知他为携带者的2／31；③Ⅳ-1夫妇生出患病孩子的概率为（3／5）×（2／31）×（1／4）=3／310。

本小题由于其亲本Ⅲ-3基因型情况为已经不确定，需分情况讨论，而Ⅳ-1表现又正常，又要改变范围求比例，因此算出Ⅳ-1为携带者概率有较大难度。根据笔者多年教学经验，学生较容易在这里出错。如果此时，丈夫的为携带者概率还要慢慢计算，此题难度就更加提高。这时直接运用数学模型，难度直接降低了一半。

综上所述，当已知常染色体隐形基因频率（m）时，可直接运用公式2／（1+1／m），快速而准确地得知显性表现人群中携带者的概率，化繁为简，极大节约遗传计算的时间，更是明显提高准确率。