基于混合模拟退火算法的阵列侧向测井实时反演研究

冯 进， 倪小威， 杨 清， 管 耀， 刘迪仁

（1. 中海石油（中国）有限公司深圳分公司研究院，广东深圳 518054；2. 中国石油塔里木油田分公司油气田产能建设事业部，新疆库尔勒 841000；3. 油气资源与勘探技术教育部重点实验室（长江大学），湖北武汉 430100；4. 长江大学地球物理与石油资源学院，湖北武汉 430100）

电阻率测井资料往往受钻井液侵入和井眼、围岩等环境因素的影响，不能准确反映钻井液侵入剖面信息，故需要对其进行反演或校正处理[1-6]。早期为解决电阻率失真问题，油田现场多采用图版校正法[7]。这种方法操作比较简便，但需要多次进行插值处理，且无法反映全部地层情况，准确性和普适性都较低[8]。

随着计算机技术的发展，线性反演技术被引入电测井资料处理[9-10]。其中，马奎特算法是一种线性反演算法，其收敛速度极快，有利于测井资料的实时反演，但在实际应用中其反演结果受初始值影响极大，若初始值设置不合理，很难准确反演出地层的真实电阻率值[11]。为了提高反演精度，针对同时存在多种电测井资料的油井，提出了联合反演的技术思路，通过增加反演过程中的地层信息来提高反演精度，此类方法具备一定的理论可行性[12]，但实际上极少有油井进行2 种以上不同原理的电测井作业，因此其普适性并不高。阵列型电测井仪器（如阵列侧向测井仪器、阵列感应测井仪器）的探测深度深、分辨率高[13-14]，能够提供多条测井信息，可以很好地解决联合反演时存在的问题。随着反演技术的进一步发展，非线性反演算法被引入测井反演领域[15-20]。模拟退火算法是一种典型的非线性反演算法，具备较强的全局搜索能力，在计算时间充足的情况下基本上能找到全局最优解；但模拟退火算法在处理复杂的非线性优化问题时收敛速度过慢，难以满足测井资料的实时反演需求。

为解决传统模拟退火算法与马奎特算法存在的问题，笔者将2 种反演方法结合，提出了混合模拟退火算法：利用幅度差法优化了模拟退火算法的初始值选择，然后利用退火策略进行了迭代，最后将迭代过一定次数的结果作为马奎特算法的初始值，利用马奎特算法进行迭代寻优。混合模拟退火算法既保留了模拟退火算法的全局寻优能力，也很好地利用了马奎特算法的后期收敛能力，不仅能满足实时反演的要求，而且还可以进一步提高反演精度。

1 阵列侧向测井反演模型

实际测井过程中，阵列侧向测井仪器可获得由浅至深的4 条视电阻率曲线MLR1、MLR2、MLR3和MLR4。视电阻率响应可以认为是冲洗带半径rxo、冲洗带电阻率 Rxo、地层电阻率 Rt、井眼和围岩等地层参数的非线性函数[21-23]。实时反演过程中，井眼校正时忽略围岩的影响，故视电阻率可以被认为是三参数（冲洗带半径 rxo、冲洗带电阻率 Rxo和地层电阻率 Rt）的非线性函数。阵列侧向测井仪器在水平层状介质中的电阻率反演模型可表示为：

式中： f(X) 为待求目标函数； xi表示待求模型参数；i 为反演种群规模； yj为第j 种测井方法的实际测井数据； Φj为第j 种测井方法的正演响应算子，可通过模式匹配法或者有限元法得到。其中， j=1,2,3,4，分别对应MLR1，MLR2，MLR3 和MLR4（下同）。

2 混合模拟退火算法

2.1 模拟退火算法原理及步骤

模拟退火算法是在金属退火机制上演化而成的一种非线性反演算法，从概率意义上来说，模拟退火算法总能找到全局最小点[24]。其控制因素主要分为搜索空间 Ω、能量函数 f(x)、 状态转移规则 p和冷却进度表 T(x)等4 类。

模拟退火算法的一般步骤是：首先随机给定初始解，然后借助控制参数产生的一系列Mapkob 链、新解产生装置和接受准则，重复“产生新解—计算适应度函数—判断是否接受新解—接受/抛弃新解”的步骤，不断进行迭代，直到目标函数适应度达到最小。

2.1.1 初始值的选取

选取的初始值是否合适会直接影响模拟退火算法的收敛速度[25]。初始值若偏离真实值较小，模拟退火时只需进行少数迭代即可寻找到最优解；若初始值偏离真实值过大，模拟退火算法迭代次数会明显增加。为此，引入基于电阻率幅度差信息的冲洗带半径初始值选取策略，定义幅度差系数s1～s6：

式中： Mj为 视电阻率； s1为MLR4 与MLR1 的幅度差系 数； s2为MLR4 与MLR2 的 幅 度 差 系 数； s3为MLR4 与MLR3 的幅度差系数； s4为MLR3 与MLR1的幅度差系数； s5为MLR3 与MLR2 的幅度差系数；s6为MLR2 与MLR1 的幅度差系数。

利用有限元法计算得到的s1～s6随冲洗带半径的变化关系如图1所示。

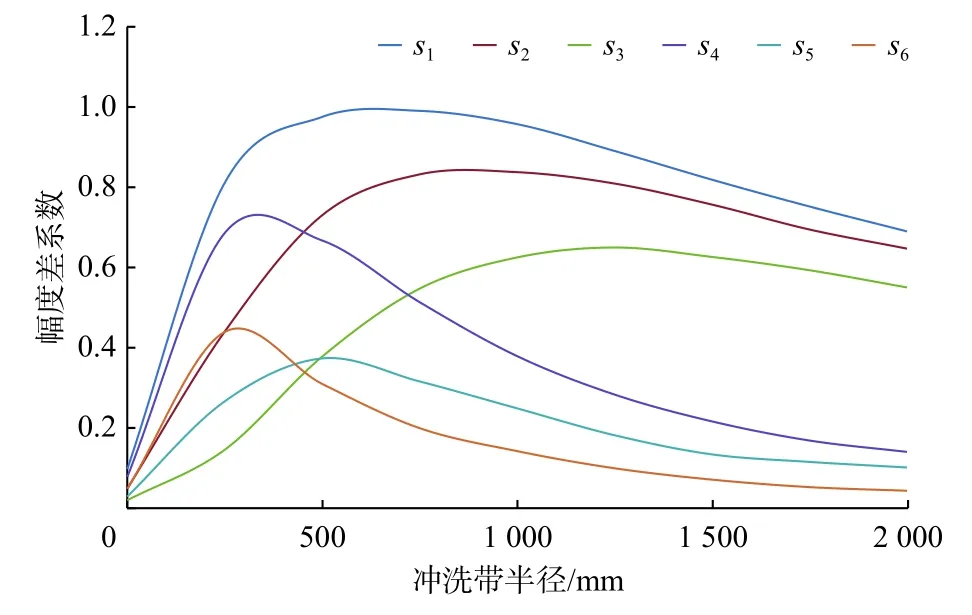
图 1 幅度差系数随冲洗带半径的变化关系Fig. 1 The relationship between the coefficient of amplitude difference and with the radius of the flushing zone

基于图1 分析冲洗带半径 rxo与 s1， s2， s3， s4， s5和s6的 多元回归关系，得到 rxo的回归关系式：

将冲洗带半径多元回归结果与理论计算值进行相关性分析，可以看出R2高达0.984 4，说明了多元回归的准确性（见图2）。

图 2 多元回归结果与理论值相关性分析Fig. 2 Correlation analysis between the multiple regression results of flushing zone radius and the theoretical values

对于冲洗带电阻率及地层电阻率，分别将微球型聚焦测井结果RMSF 及MLR4 作为其初始值。

2.1.2 新解的求取

在初始值的基础上进行新解的求取， rxo， Rxo和Rt分别按照以下公式进行迭代更新：

式中： Tk为退火温度； T0为初始温度，一般数值较大； k 为迭代次数； Rtnew为地层电阻率新解， Ω·m；Rxonew为 冲洗带电阻率新解， Ω·m ； rxonew为冲洗带半径新解，mm； Rtmax， Rtmin为地层电阻率的最大、最小值， Ω·m ； Rxomax， Rxomin为冲洗带电阻率的最大、最小值， Ω·m ； rxomax， rxomin为冲洗带半径的最大、最小值，mm； rand 为0 到1 之间的随机数； sign(x)为符号函数，当x 大于等于0 时为+1，当x 小于0 时为-1。

2.1.3 接受准则

采用Metropolis 准则，判断是否接受模拟退火算法产生的新解[26]：

式中：p（Tk）为接受新解的概率；f（A），f（B）分别为原始解、新解对应的系统能量（即适应度）。

若新解对应的系统能量 f(B)小于前一状态系统能量 f(A)，则直接接受新解；反之，若新解系统能量f(B)( 大于或者等)于前一状态系统能量 f(A)，则以的概率接受新解；接受的新解作为下一次迭代的初始值。

2.1.4 终止条件

采用温度终止准则[27]，若系统温度大于预先设定的系统最低温度，则继续进行迭代；若系统温度小于或等于系统最低温度，则算法终止。

2.2 混合模拟退火算法

采用模拟退火算法对式（1）进行求解，迭代若干次（一般15 次左右），将迭代后的新解作为初始值，利用马奎特算法进行反演处理，即可得到三参数反演结果。

将利用模拟退火算法得到的初始值带入正演模型，将阵列侧向测井响应在该初始值附近线性化：

式中： Mja为视电阻率响应， Ω·m。

视电阻率拟值矩阵和测井数据矩阵分别表示为：

式中： ΔP 为未知参量矩阵； [J]为Jacobi 矩阵。

式（18）采用阻尼最小二乘法进行求解，即可实现三参数反演。混合模拟退火算法的基本步骤为：

1）设定初始温度、最低温度和退火因子等参数数值；

2）基于电阻率幅度差信息策略生成初始值，并计算初始值对应的适应度；

3）将初始值代入式（9）—式（12），进行模拟退火操作，利用Metropolis 准则判断是否进行个体更新；

4）利用模拟退火算法迭代一定的代数（具体根据实际问题而定），将新解作为初始值代入马奎特算法；

5）当迭代次数达到最大值或者适应度值小于预先设定的阈值时，将此时的新解作为反演结果输出；若不满足收敛条件，则跳转至步骤2）重新进行初始计算。

3 混合模拟退火算法准确性评价

算法的性能评价主要包括寻优成功率、收敛平均代数、平均最优适应度和最优个体进化曲线等方面[28-29]。马奎特算法、模拟退火算法和混合模拟退火算法的寻优成功率、收敛平均代数及平均最优适应度的对比分析如表1 所示，混合模拟退火算法反演时长与仪器测量时长的对比结果如表2 所示。

表 1 3 种算法的性能对比Table 1 Comparison of the performances with three algorithms

表 2 混合模拟退火算法反演时长与仪器测量时长对比Table 2 Comparison of the inversion time of hybrid simulated annealing algorithm with the instrument measurement time

从表1 可知，混合模拟退火算法寻优成功率远高于马奎特算法，且收敛速度远高于模拟退火算法，不仅很好地兼顾了马奎特算法、模拟退火算法的优点，而且避免了二者的缺点。从表2 可以看出，混合模拟退火算法的反演速度快于仪器测量速度，满足实时反演的要求。

3 种算法的最优个体进化曲线如图3 所示。从图3 可以看出，混合模拟退火算法较模拟退火算法及马奎特算法的初始适应度更小，说明基于电阻率幅度差信息的初始值优化策略的有效性。混合模拟退火算法适应度小于0.005，反演精度高。

图 3 算法最优个体进化曲线Fig. 3 Optimal individual evolution curve with three algorithms

4 应用实例

选取W1P-7 井1 880.00～2 020.00 m 层段进行反演处理，处理结果如图4 所示。W1P-7 井岩电参数a=1，b=1，m=1.72，n=1.87。图4 中：第一道为岩性曲线道；第二道为为电阻率资料道，其中RMSF 为微球型聚焦测井视电阻率，MLR1C—MLR4C 为阵列侧向测井经过井眼校正之后的视电阻率曲线。从岩性曲线道可以看出，1 982.00～1 992.00 m 层段的伽马曲线表现出明显的砂岩特征；同时，该层段的电阻率曲线也表现出明显的幅度差特征，可以确定1 982.00～1 992.00 m 层段为渗透层。第三道为反演电阻率道，第四道为根据电阻率反演结果计算的含水饱和度。根据计算的含水饱和度，可以非常直观地显示出在处理层段的顶部、底部分别存在一油层和一水层，分别命名为W1 层和W2 层。根据试油资料，井深1 990.00 m 处累计泵抽0.83 h，泵抽地层流体达24.49 L，流体性质为油，证明W1 层为油层；井深2 002.01 m 处累计泵抽2.70 h，泵抽地层流体达83.86 L，流体性质为地层水，证明W2 层为水层。试油结果与反演处理结果一致，表明了混合模拟退火算法的正确性与实用性。

图 4 W1P-7 井反演处理结果Fig. 4 Inversion processing results of Well W1P-7

5 结论与建议

1）提出基于电阻率幅度差信息初始值选取策略的混合模拟退火反演算法，理论模型与实际资料验证表明，该算法不仅保存了传统实时反演方法的速度优势（单点反演耗时仅需0.2 s 左右），还进一步提高了反演精度，同时三参数反演结果与试油结果相匹配。

2）以往的电阻率测井反演算法往往以单一算法为主，算法收敛性和寻优能力不能同时得到保证，混合模拟退火算法兼顾了收敛速度和寻优能力，反演精度更高。

3）本文的研究有一定局限性，冲洗带半径初值生成公式只适用于单一阵列侧向测井仪器，实际应用中应根据阵列侧向测井仪器种类结合本文方法重新生成初始值公式。此外，支持向量机、差分进化算法等非线性反演算法比模拟退火算法的寻优能力更强，建议进一步研究此类算法与线性反演算法的混合反演应用，以得到更好的反演效果。