起伏振动状态下水平管内两相流多尺度熵分析

周云龙， 常 赫， 赵 盘

(东北电力大学 能源与动力工程学院，吉林 132012)

两相流现象广泛存在于化工及核反应堆等领域[1]。近年来随着核动力船舶技术的快速发展，对漂浮式核电站及核除盐设备的研究成果日益增多[2-4]。受海洋中自然条件影响，倾斜、摇摆及振动等情况会影响核动力装置中气液两相的流动状态[5-6]，从而影响反应堆安全性能[7]。已有研究表明，摇摆引起的附加惯性力可以改变气液两相流型及摩擦阻力[8-9]。同时，肖秀等[10]通过研究振动对环管内两相流影响的研究发现，振动会对两相流参数分布产生一定影响，随含气率的增大，影响减弱。Pendyala等[11-12]通过研究振动工况下垂直管内两相流动及压降，得出低频振动可以加大流体流速及压降波动。两相流是一个复杂的非线性动力学系统，由于气液相界面存在复杂的界面效应，其内部流动结构变化与压力波动信号有着紧密的联系[13-14]。

熵是系统复杂性和规则性的一种测度，自Pincus等[15]提出近似熵后，在各领域均得到广泛应用。针对近似熵算法存在的对数据长度敏感的问题，Richman[16]提出了适用于复杂信号处理的样本熵算法。研究表明，多尺度熵算法可以在生理及生物等复杂信号多时空尺度表征方面进一步识别复杂的研究对象[13]。在两相流领域，周云龙等[17]通过采用不同方法分析7×7棒束通道气液两相流压差信号，得出多尺度熵方法在流型识别方面优于R/S分析法。郑桂波等[18]采用多尺度熵算法研究电导波动信号，发现小尺度下样本熵的变化速率特征可以明显区分不同流型。Zhou等[19]对棒束通道内压差信号进行多尺度熵分析，发现该方法可以在不同尺度上表征不同流动工况下流体的动力学特性，且小尺度下的多尺度熵率可以精确识别典型流型。

本文通过实验的方法研究了起伏振动状态下气液两相流型及压差波动信号，采用多尺度样本熵方法对其进行数据分析，重点探讨了多尺度熵变化速率以及不同尺度下熵值变化特征，以期进一步揭示振动对流体流动的影响并为流型识别提出一种新的方法。

1 多尺度熵理论

1.1 多尺度熵算法

样本熵(SampEn)是近似熵的改进算法，多尺度熵(MSE)计算是粗粒化处理原始时间序列后对各尺度计算其样本熵。具体算法如下：

(1)给定原始时间序列{x(i)∶i=1,2,3,…,N}。对其进行变换，构建长度为N=L/τ粗粒化时间序列

(1)

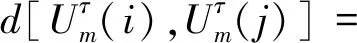
0≤k≤m-1}

(2)

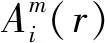
(3)

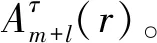
(5)在多尺度熵计算中，容限r为取始时间序列标准差(SD)的0.1～0.25倍[20]，m为2，计算粗粒化后各个尺度对应时间序列的样本熵值，得到多尺度熵

MSE={τ|SampEn(t,m,r,N)=

(4)

1.2 典型信号多尺度熵分析

图1所示为包含正弦噪声及高斯白噪声在内的几种典型信号下的多尺度熵特征，其产生条件如下：

(1)Lorenz方程

dx/dt=-σx+σy

dy/dt=rx-y-xz

dz/dt=-bx+xy

给定σ=16，r=45.92，b=4，初始条件为x=-1,y=0,z=1。

(2)正弦信号y=3sinx。

(3)正弦+噪声y=3sinx+py1

其中y1是高斯白噪声序列，p是随机成分所占比例，设p=0.2。

如图1所示，高斯白噪声的熵值随尺度增大呈下降趋势，与之相比，1/f噪声熵值整体趋于稳定，Costa等[20]研究发现该噪声在多个尺度都存在复杂的结构，符合图1所示特征。Lorenz序列样本熵值变化形式相对复杂，熵值在前5个尺度上平稳增加，6到10尺度保持稳定，随之显著增大至17个尺度后平缓减小。其变化趋势显示该序列复杂度更高。正弦信号加噪前后熵值变化趋势一致，且熵值较低，平稳增大到第6个尺度后基本保持恒定，符合其具有周期性和规则性的特点。综上所述，多尺度样本熵算法不仅具有一定的抗噪性，还可作为确定性工具来分析复杂的时间序列。

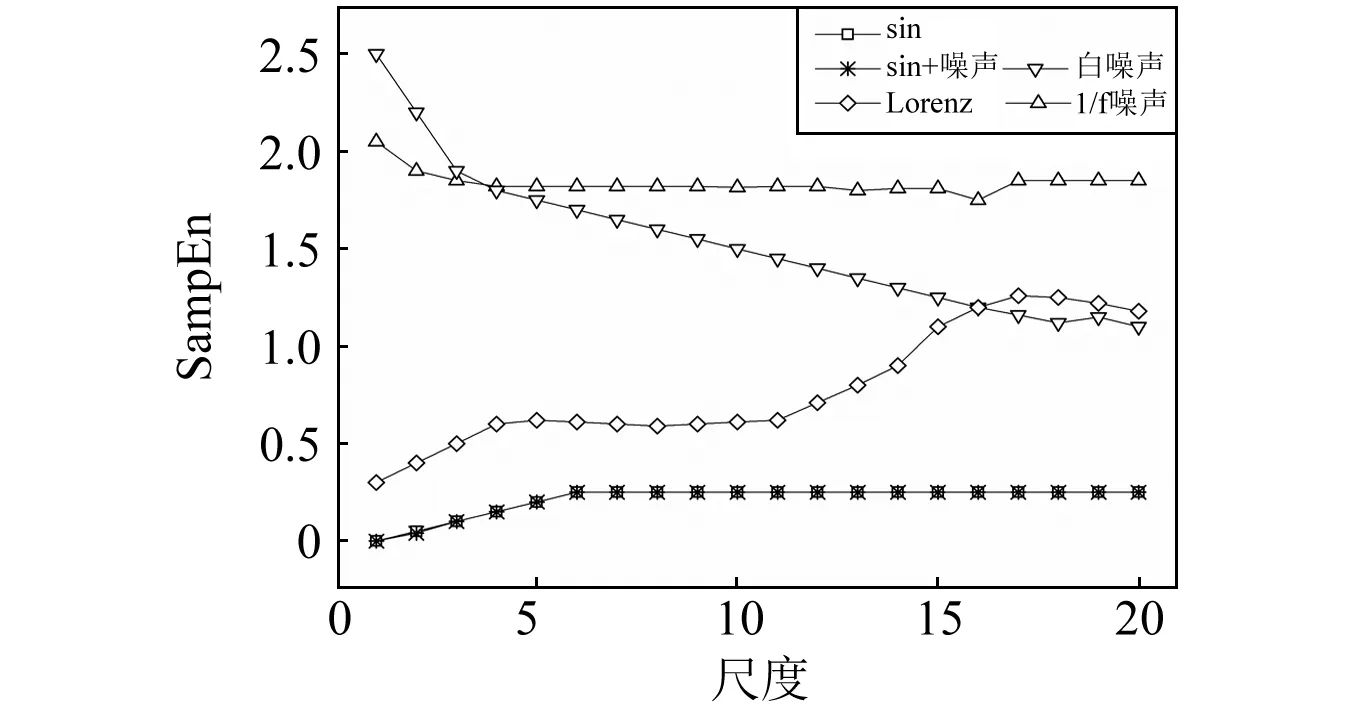
图1 典型信号时间序列多尺度熵Fig.1 Multi-scale entropy of typical signal time series

为研究序列长度对于某一特定流型的多尺度熵值的影响，本文选取了四种不同的序列长度，研究了沸腾波状流条件下的多尺度样本熵特征，如图2所示。

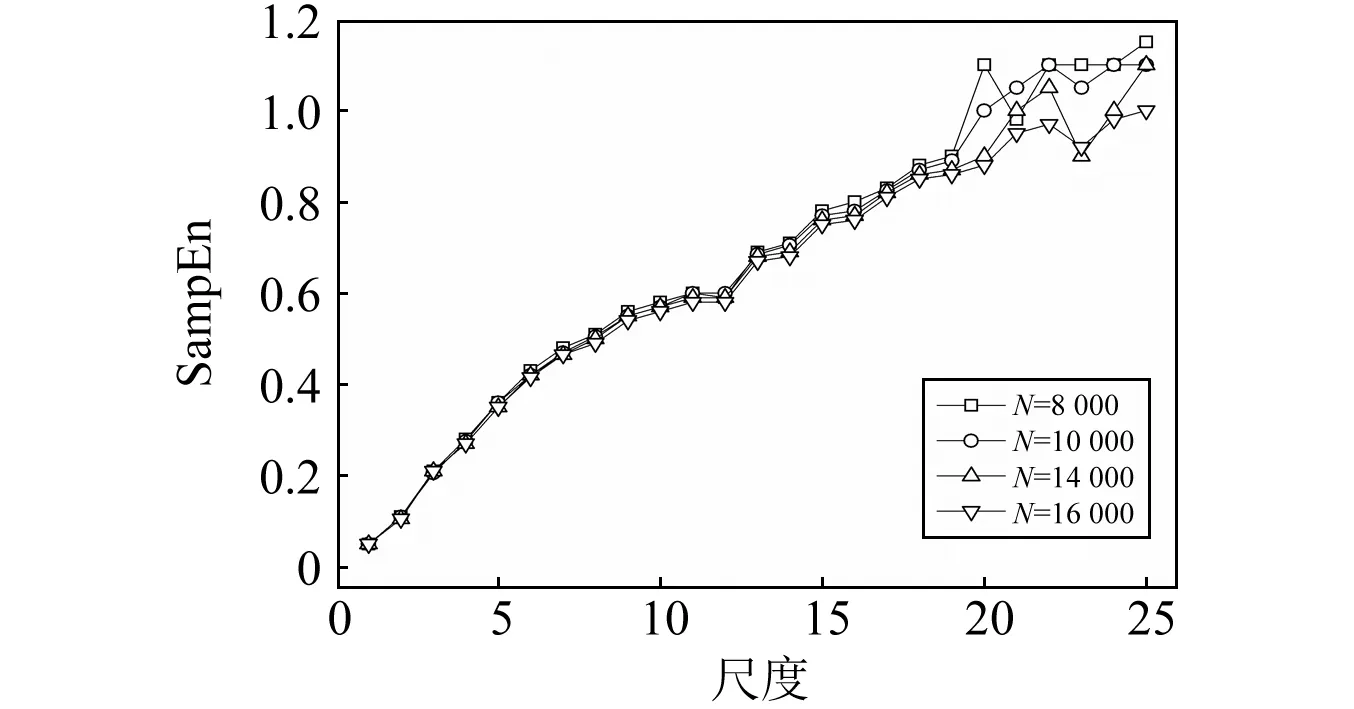
图2 沸腾波状流流动条件下不同序列长度多尺度熵Fig.2 Multi-scale entropy of different length of boiling wave flow

从图2可以发现，不同序列长度上特定条件下的多尺度熵值变化趋势大体相同。在第11个尺度均呈现下降趋势，缓慢增加至19个尺度后出现振荡现象，充分表明多尺度熵在数据长度上的鲁棒性。为保证展现信号演化过程的完整性，同时加快运算速度，本文研究中所选序列长度为8 000。

2 实验原理及结果

2.1 实验装置简介

本实验将如图3所示的两相流实验回路与振动装置结合，对水平通道内气液两相流进行研究分析，实验装置介绍及实验方法详见参考文献[21]。实验段采用管径为35 mm、长度为2 m的透明有机玻璃管，将其水平固定于振动台上，如图4所示。两个测压孔分别位于实验段两端，并与压差变送器相连，通过数据采集仪采集数据。实验在常温常压下进行，水平通道随振动台自身振动做正弦运动，气体体积流量范围是0.2～60 m3·h-1，液相体积流量范围是0.3～7 m3·h-1，利用高速摄影仪记录气液两相流型。

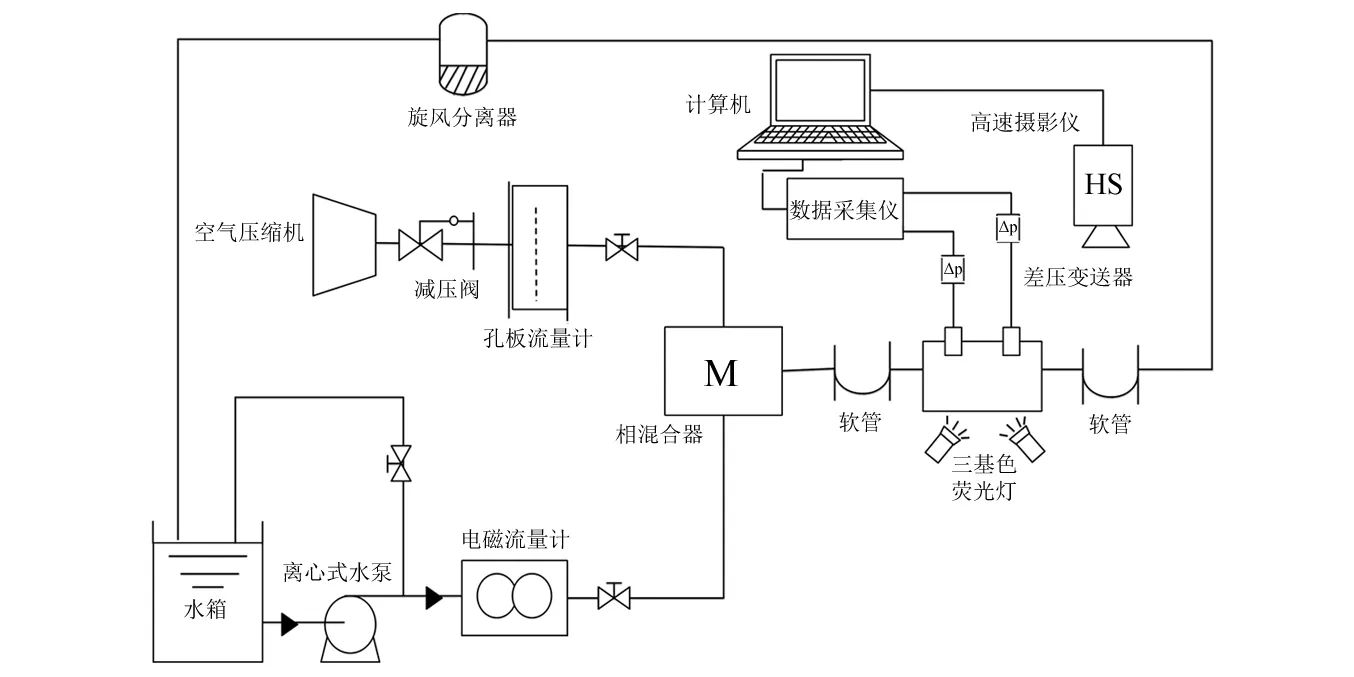
图3 实验系统流程图Fig.3 Schematic diagram of experimental apparatus

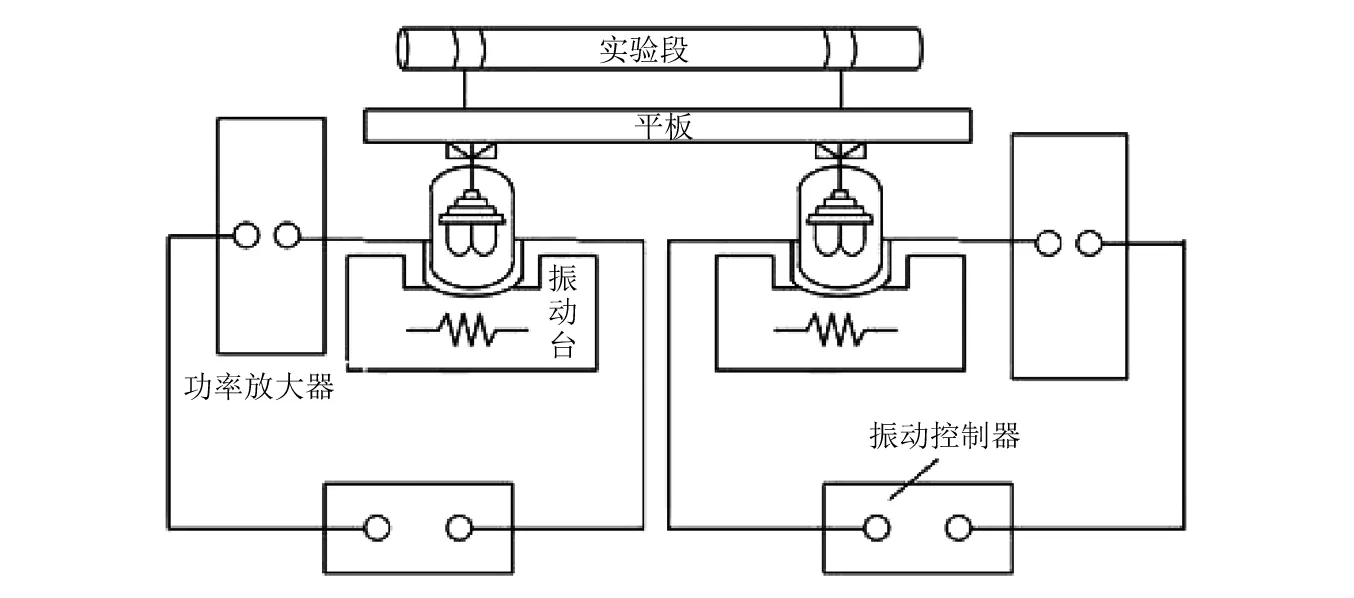
图4 振动装置示意图Fig.4 Schematic diagram of vibration apparatus

2.2 实验结果

通过高速摄影仪记录的图像及可视化观察发现，振动状态下水平通道内气液两相流动状态不同于稳态工况，其主要流型包括：泡状流，珠状流，炮弹流，弹状-波状流，沸腾波状流及环状流。不同振动工况，如高频低幅式振动或低频高幅式振动等工况影响流型转换界限，关于流型特点及流型图的介绍详见参考文献[22]。

经过大量实验发现，流型在低频率振动状态下变化并不明显，为此，本文针对振动频率为8 Hz，振动幅度为5 mm的工况进行压差信号采集。各典型流型的压差波动信号,如图5所示。

如图5所示，与稳态工况下通道内气液两相流压差波动信号相比，起伏式振动状态下管内压差波动信号较为剧烈，波动信号变化频率快，振动过程中还会出现负压，其原因在于振动引起的流动不稳定性与管内气液两相流体相对运动共同影响了压差波动信号。同时，与稳态工况类似，各典型流型间的压差波动曲线差异明显，可依此识别起伏式振动状态下管内气液两相流型。

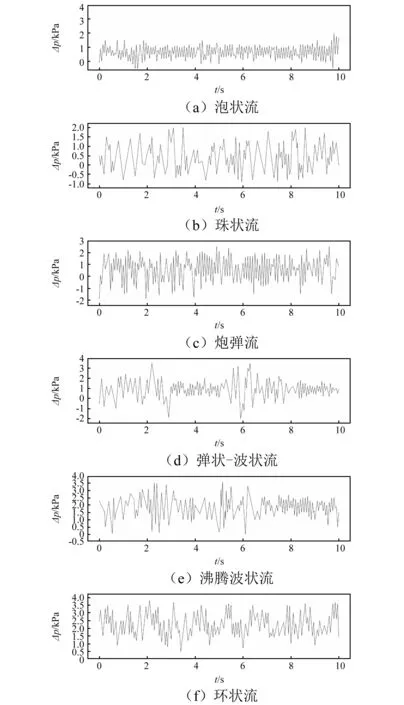
图5 典型流型压差波动信号Fig.5 Pressure fluctuation signal of typical flow regime

3 两相流多尺度熵

3.1 动力学特性分析

对上述几种典型流型压差信号进行多尺度熵分析，参考已有文献[23]及相关实验数据，得出在气液两相流动计算中r取原始时间序列标准差的0.12倍，序列匹配长度m=2时，其适用性较好。同时为保证运算速度及准确性，确定最大粗粒化程度为25，数据长度为8 000点。

图6和图7分别显示了液相体积流为1.73 m3·h-1和0.746 m3·h-1时不同气相流量下压力波动信号的多尺度熵值计算结果。

对比图6和图7可发现，两种液相流量工况下其多尺度熵特征变化具有一致性：前5个尺度上熵值平稳增长，但随着尺度的增大，不同流型间熵值变化趋势存在明显的差异性。同时，对比不同流型间熵值大小可发现，泡状流整体熵值最大，环状流最小。由此可说明泡状流中流体运动轨迹最为复杂，环状流复杂程度较低。

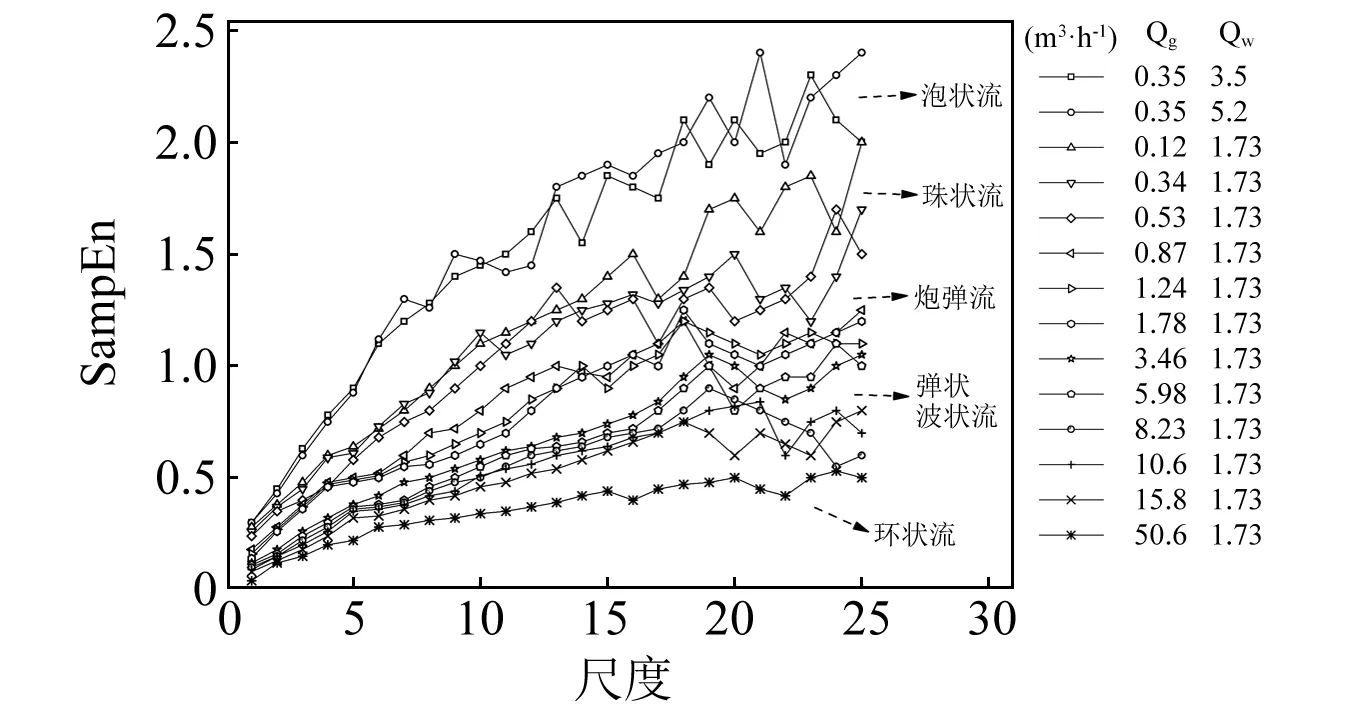
图6 不同流型压差信号波动信号多尺度熵Fig.6 Multi-scale entropy of pressure fluctuation signals under different flow regime

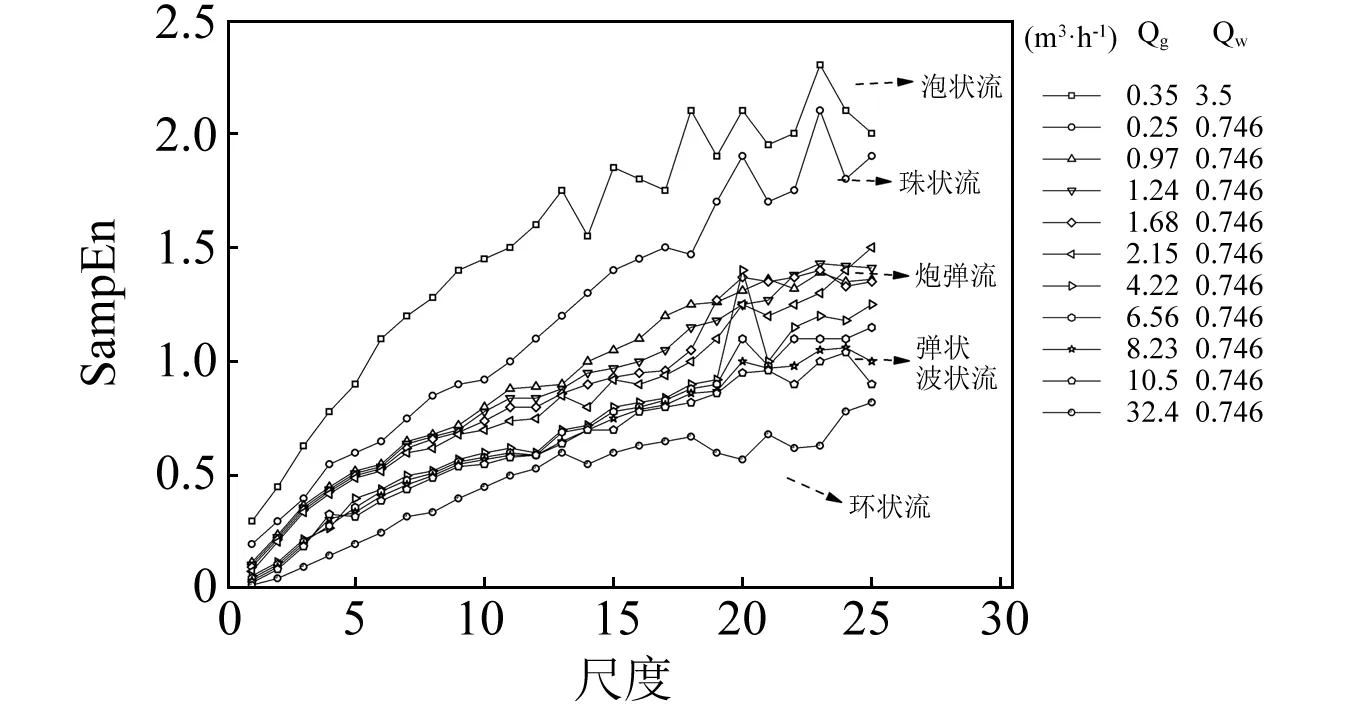
图7 不同流型压差信号波动信号多尺度熵Fig.7 Multi-scale entropy of pressure fluctuation signals under different flow regime

针对各个尺度上不同流型熵值变化规律可发现，前5个尺度上不同流型的熵值增长率出现了显著差异，泡状流增长最快，环状流增长速率最低；从第6个尺度开始，泡状流熵值随尺度增大而增大并伴有明显的振荡现象；珠状流熵值与泡状流熵值变化趋势一致，并出现大幅度波动，但增长速率及熵值均小于泡状流；炮弹流作为一种过渡流型，其熵值变化趋势较为平缓，以一定速率随尺度增大稳定增大，没有明显的熵值振荡；沸腾波状流熵值随尺度增大平缓增长的过程中出现了小幅振荡，并伴有一定的降低趋势；环状流作为熵值最低的流型，其变化速率也最小，且在大尺度时熵值趋于平稳。

各流型的流动特性可以由其多尺度熵值变化特征表现，结合高速摄影仪所拍摄的各流型图片，分析如下：

(1)泡状流 泡状流中液相作为连续相，小气泡以聚集或离散的形式贴于水平通道上壁面分布，同时由于通道的振动作用，大多数气泡沿液体流动方向运动，极少数气泡随机运动，形成复杂的运动轨迹，同时产生类似于随机信号的压差波动信号，在熵值特征上表现出了高于其他流型并产生大幅振荡的现象。

(2)珠状流 稳态流动中，存在泡状流向弹状流过渡的流型，在振动条件下则转变为珠状流。随着振动作用加强，小气泡的聚合现象更为明显，逐渐形成圆珠状的大气泡随机分布于液相流体中。随着起伏振动的继续，珠状气泡不断变化大小，或黏连在一起，或离散分布于通道内。与泡状流表现出了相似的流型特征，其熵值变化趋势也与泡状流一致。

(3)炮弹流 随气相流量的增大，水平管内气泡逐渐变长，此时形成的长气泡虽不会因振动的影响而发生破裂的现象，然而很容易因触碰通道壁面而使之前的长气泡与液相发生碰撞而分隔出少量小气泡，这些小气泡会受液相流速的影响而继续运动或破灭。这种有规律的气液相交替变化使得其流动特性具有一定周期性，因而熵值较低且变化趋势较为平缓。然而与低液相流速相比，高液相流速对于小气泡的击碎作用导致了气相的随机流动现象，也使得该工况下其熵值变化趋势出现了一定振荡。

(4)沸腾波状流 沸腾波状流作为一种相对稳定的流型，类似于稳态流动状态下的分层流。气液两相分别沿管道运动，然而由于振动作用的影响，液体无规则的上下运动使得气相充满了液相间隙，遍布整个通道。随着振动幅度及振动频率的变化，气液相分布也会随之改变。与上述三种流型相比，其流体流动随机性较低，因而熵值较低。

(5)环状流 当液相流速较低而气相流速相对很高时，液体会形成环形液膜沿通道壁面流动，气相夹带小液珠快速通过通道中心区域。由于高速气流产生的推动力远大于振动附加力对于气液两相流动的影响，因此振动对该流型的影响较小，压差波动信号周期性较为明显，因而其熵值较低且稳定。

3.2 流型识别

由上述两种液相流量不同流型下压差波动信号的多尺度熵特征分析可得：该方法在不同尺度上可以很好的表明不同流型的动力学特征。由于各流型的多尺度熵值变化趋势在前5个尺度上存在明显的差异性，可将此作为一种识别流型的准则。该部分将前5个尺度不同流型熵值用最小二乘法进行线性拟合，进而得到斜率，反应在样本熵上即其增长速率，定义为多尺度熵率。

针对102种流动条件，其多尺度熵率分布情况如图8所示。观察图8可发现，不同流型的多尺度熵率分布差异性较大：泡状流分布范围在0.13～0.18，珠状流基本分布于0.11～0.13，弹状-波状流和炮弹流为0.07～0.11，沸腾波状流位于0.05～0.07之间，而环状流的多尺度熵率基本在0.05以下。由于弹状-波状流和炮弹流属于过渡流型，流型特征具有一定相似性，采用该方法不易区分。在其他流动条件下，其识别准确率达到94%以上。因而多尺度熵率可以较好的识别起伏振动状态下水平通道内气液两相典型流型。

图8 不同流动条件的多尺度熵率Fig.8 Multi-scale entropy rate of different flow conditions

4 结 论

(1)与稳态工况相比，起伏振动状态下水平管内气液两相流型主要包括泡状流、珠状流、炮弹流、弹状-波状流、沸腾波状流及环状流。其特有流型主要包括 炮弹流及沸腾波状流，且振动对流体流动特性及压降均会产生一定影响。

(2)多尺度熵作为一种非线性分析方法，可以很好的揭示气液两相流的动力学复杂性，如泡状流及珠状流流体流动随机性较大，具有较高熵值及波动性，环状流熵值最低且平缓。

(3)依据多尺度熵的不同变化趋势，得出多尺度熵率，其值可以较好的识别振动状态下气液两相流型中的典型流型。因而可作为一种新的准则用来识别流型。

(4)运用多尺度熵对各流型压差波动信号进行分析，不同流型熵值变化趋势差异显著。利用小尺度下样本熵的变化速率特征可以明显区分水平通道内气液两相流型，而大尺度下样本熵的变化特征可以反映不同流型的动力学特性。