超声电机在冲击环境中的性能研究

孙 栋， 唐玉娟， 王 炅， 王新杰

(1.南京理工大学机 械工程学院，南京 210094；2.金陵科技学院 智能科学与控制工程学院，南京 211169)

超声电机(USMs)作为近二十年来发展迅速的一种驱动器，有着响应快，体积小，设计灵活、断电自锁等诸多优势，目前已广泛应用于机器人，信息技术，医疗及精密定位平台等领域[1-4]。此外，超声电机还在空间探索领域展现出广阔的应用前景[5-6]，研究人员为此展开了超声电机在高低温[7-8]和真空[9]等极端环境下的性能研究。部分研究人员还将目光投向了武器系统，诸如飞行器中的智能羽翼控制，隐身技术[10]以及智能引信安全系统[11]等。冲击，作为极端环境的一种，不仅仅存在于武器系统中，还广泛的存在于航天系统与机械结构中。为了拓展超声电机的应用领域，有必要开展冲击环境下超声电机的性能研究。任金华等利用有限元方法对旋转型超声电机建模，分析了电机在10 000 g静态过载下的应力分布情况[12]。陈超等分析了超声电机的失效模式，并利用LS-dyna评估了超声电机所能够承受的极限过载情况，测试了不同冲击过载之后超声电机的机械特性,但是其建立的是二维模型，不能准确的反映出电机在冲击环境中的变化过程[13]。Hou等[14]通过仿真的方法得到了一种新型电机在冲击载荷下的动态响应过程，但缺乏实验测试验证。唐玉娟等分析了典型引信环境力对其所设计的直线型超声电机的影响，并进行过载实验，实验证明该直线型超声电机能够耐受15 000 g的过载[15]。我们在之前的研究工作中建立了旋转型超声电机在冲击环境下的动态响应理论模型，但该模型中采用了刚塑性材料模型，有着一定的局限性[16]。

综上所述，国内外学者已经对冲击环境中超声电机的失效模型、动态响应过程等展开了初步的模拟与研究。但目前仍然存在着失效模式分析简单；模型不足以准确的反映电机的动态过程；实验测试不够全面等问题。本文针对超声电机中的关键部件，通过有限元方法，建立旋转型超声电机的三维模型，且结构材料采用更接近工程实际的双线性随动硬化模型；通过有限元方法得到冲击环境下超声电机的动态响应过程，并分析柔性转子在不同冲击环境下的不同变形过程；通过数值方法，得到转子变形量与预紧力之间的关系。最后通过马歇特捶进行冲击实验，测试了冲击载荷对电机机械性能与定子振动特性的影响，并实验证明了橡胶在冲击环境下对超声电机的保护作用。

1 冲击环境超声电机的动态响应

超声电机是一个复杂的机电耦合系统，其在冲击载荷下的失效模式主要包括：定子与转子的变形导致预紧力的降低或消失、定子变形导致的振动频率的漂移或振型的畸变以及压电陶瓷的脱胶或断裂。对于旋转型超声电机而言，定子和压电材料的结构强度远远超过转子，因此转子在冲击环境中更容易变形。

1.1 有限元模型

以旋转型超声电机TRUM60作为分析对象，超声电机的部件包括定子、转子、压电陶瓷，基座以及输出轴等，如图1(a)所示。在冲击环境中，结构之间的相互碰撞使得转子有向上运动的趋势，而端盖与轴承将限制转子的向上运动。因此在有限元模型中新增限位片用于模拟端盖与轴承对转子的限制作用，并忽略了底座与端盖，仅保留了压电陶瓷，定子，转子，输出轴，在有限元软件workbench中建立的模型如图1(b)所示。为了尽可能的接近实际工程情况，定子与转子采用双

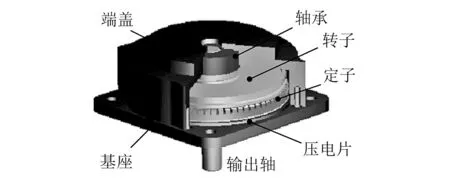
(a) TRUM60电机的示意图

(b)有限元模型 图1 超声电机的结构与有限元模型Fig.1 Structure and finite element model of a travelling wave rotary ultrasonic motor

线性随动硬化模型材料。输出轴的强度很大，采用线弹性模型。各个部件的材料参数如表1所示。冲击过程中各个零部件将会产生复杂的相互作用，定子与压电陶瓷片通过胶水粘贴，这里忽略胶层，并设定为绑定约束bonded；定转子设定为摩擦接触，摩擦因数设定为0.2[15]；转子与输出轴固接，在模型中设为bonded约束；输出轴实际中只会上下运动，因此在分析时限制其在x与z方向上的自由度；定子的内边界设为固支。

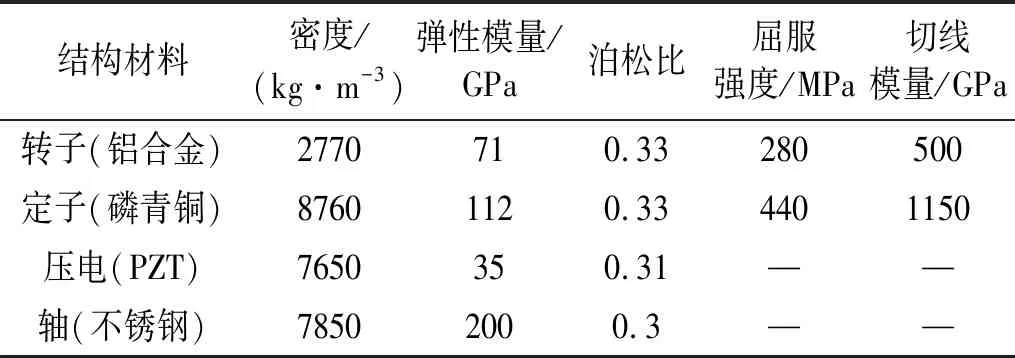
表1 模型材料参数Tab.1 Parameters of model material

1.2 冲击载荷作用下超声电机的动态响应分析

图2为超声电机在经历幅值2 000 g，脉宽1 ms的半正弦冲击载荷后不同时刻的变形情况。冲击方向沿着电机输出轴的轴向，即y轴正向。当冲击刚刚发生时，输出轴质量大，转子的刚度小，输出轴带着转子中心向下运动，直到位移最大的值，如图2(a)所示。由于定转子的弹性作用，输出轴与转子弹回，并与限位片碰撞，如图2(b)所示。此后，定子与转子以及转子与限位片之间的相互碰撞，使得结构进入复杂的衰减振动状态，转子不再是一个稳定的圆盘，而是呈现出一种扭曲振动状态，如图2(c)所示。整个过程中，定子的最大应力为380 MPa，小于磷青铜的屈服极限，这表明定子没有产生塑性变形，如图2(d)所示。

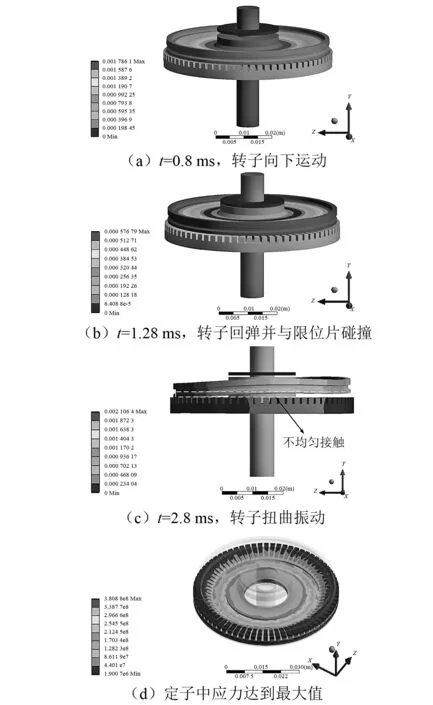
图2 超声电机冲击载荷下的动态响应Fig.2 Dynamic response of ultrasonic motor and stress distribution in stator

图3表示了定转子的最大/小相对位移时程曲线，其中相对位移指的是定子或转子内边缘相对于外边缘的位移。由于定转子在冲击中会产生复杂的相互作用，因此将相对位移分为最大与最小相对位移，分别表示定转子内边缘位移的最大/小值与外边缘位移最大/小值之差。从图3可以看出，定转子相对位移的峰值与加速度峰值相比，有着0.3 ms的时间延迟。定子的相对位移曲线在y=0 mm左右衰减震荡，说明定子强度大，没有产生永久变形，这与图2(d)的结果相对应。转子的相对位移曲线一直在y<0处衰减震荡，这说明转子的强度小，冲击之后转子的中心下沉，产生了不可逆的塑性变形。

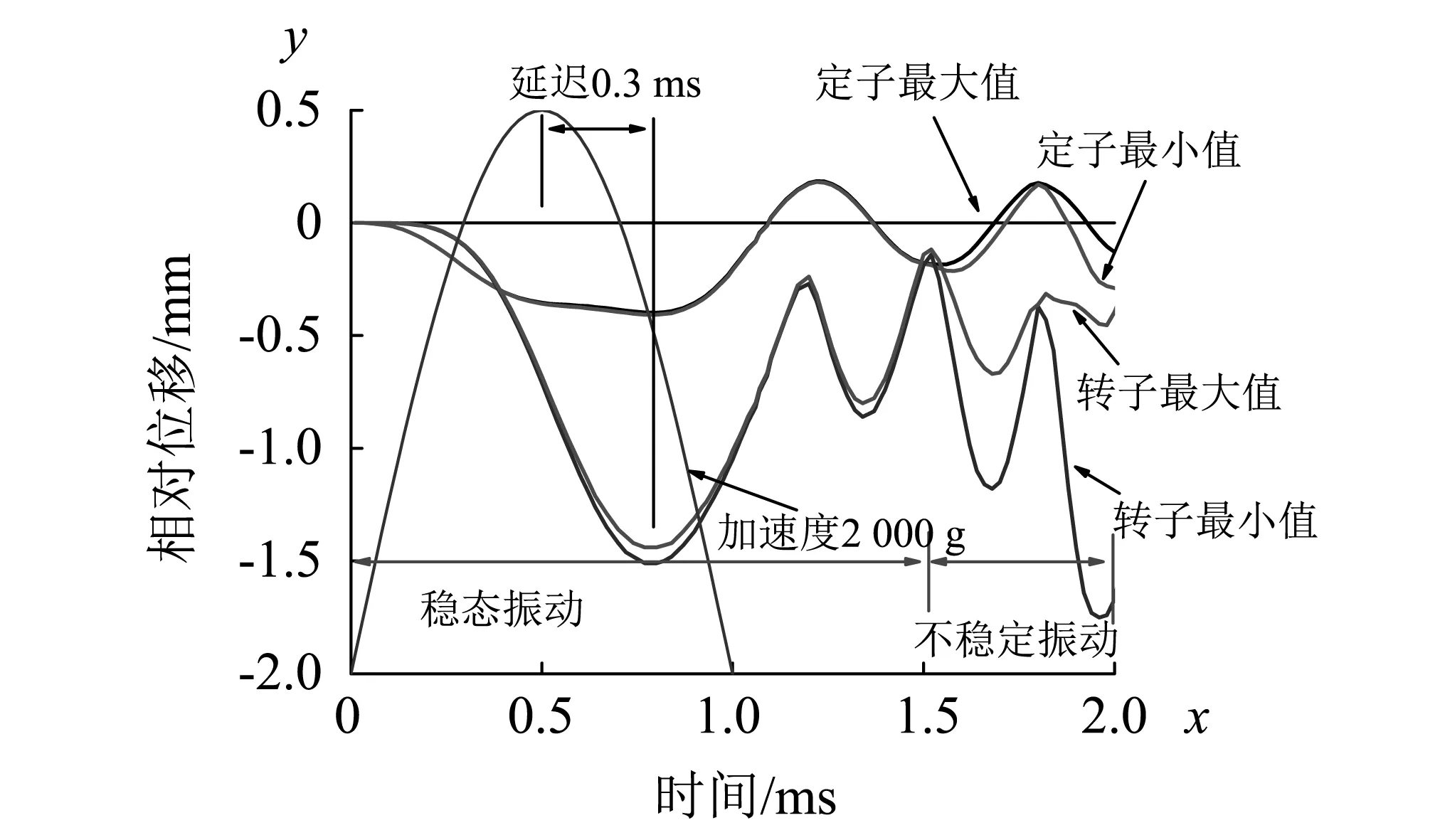
图3 定转子的相对位移时程曲线Fig.3 Relative displacement time history response of stator and rotor

冲击刚发生时，转子的最大与最小相对位移曲线基本重合，说明此时转子的中心随着输出轴的往复运动而上下振动，转子外边缘保持着一个稳定的圆环，此时是一种稳定的振动状态。但随后转子的最大与最小相对位移曲线逐渐分离，这是由于结构之间的相互碰撞，导致转子呈现出一种扭曲的振动状态，整个转子不再是一个稳定的圆盘，与图2(c)的结果相对应。转子的扭曲振动将导致转子的扭曲变形，使得转子与定子的产生不均匀接触，图2(c)中虚线框清晰显示出转子与定子之间有着不均匀的间隙。定子的最大与最小相对位移曲线基本一致，这说明定子的强度大，振动状态也相对稳定。

由此可见，冲击载荷对转子的影响主要分为两种状态：①转子产生不可逆的塑性变形，转子的中心下沉。②在冲击结束过后，转子冲击过程中的扭曲振动导致转子产生扭曲变形，使得定转子的接触界面不均匀。

1.3 动态响应与幅值脉宽之间的关系

超声电机的动态响应过程不仅仅取决于冲击载荷的幅值，还取决于冲击载荷的脉宽。本节主要考察不同幅值与脉宽条件下超声电机的动态响应过程。由于定子的强度大，不易变形。这里仅查看观察转子的最大相对位移时程曲线。图4(a)为冲击脉宽为1 ms，幅值从1 000 g逐渐增加到3 250 g时转子的最大相对位移时程曲线。显然随着冲击幅值的增加，转子最大相对位移的峰值也不断增加，当幅值达到3 000 g之后，转子的最大相对位移峰值达到2.1 mm左右之后就不再增加，且位移峰值出现的时刻提前，曲线的脉宽变窄。这一现象出现的原因是冲击幅值较小时，转子的回弹主要依靠的是转子本身的弹性作用；随着冲击幅值的不断增加，转子中心的下沉量不断增加，而定子的内边界固支，最终转子中心将会与定子中心碰撞，如图4(b)所示，这导致了转子最大相对位移曲线的峰值出现的时刻提前，曲线的脉宽变窄。定子内边界与转子中心环的距离为2.5 mm，仿真结果显示冲击后定子外边缘向下运动的位移在0.4 mm左右，因此转子的最大相对位移的峰值在达到2.1 mm左右之后就不再增加。

图4 不同幅值与脉宽冲击载荷下转子位移的时程曲线Fig.4 Simulated displacement-time curves of rotor under impact with different amplitude and duration

图4(c)为冲击过载的幅值为2 000 g，脉宽从0.25 ms到4 ms逐渐增加时转子的最大相对位移时程曲线。当脉宽为1ms时，转子的最大相对位移曲线峰值最大，且最大相对位移峰值从大到小对应的脉宽分别为1 ms，0.5 ms，2 ms，0.25 ms与4 ms。对超声电机的整体结构进行模态分析，其在纵向方向即y方向上对应的振型如图5所示，频率为860.47 Hz。而脉宽0.5 ms与1 ms的对应频率为1 000 Hz与500 Hz，最接近模态振动频率860.47 Hz，其产生的相对位移也较大。这说明冲击载荷的频率接近结构谐振频率时，结构将产生大的变形。

图5 纵向振型Fig.5 Vertical vibration mode

1.4 转子变形与预紧力关系

定转子之间通过预紧力紧密接触，并通过摩擦力将定子的高频微幅振动转化成转子的宏观动作。预紧力对超声电机的性能至关重要[17-18]。正常状态下，转子与轴承有薄垫片，迫使转子产生弹性变形，使得定转子之间紧密接触。假设弹性垫片的厚度为0.3 mm，通过有限元方法，计算得到定转子之间的预压力为229.71 N。根据1.2节中的仿真结果，转子在冲击载荷作用下的变形主要分为两种：①转子中心下沉导致定转子之间预紧力的减少甚至消失；②转子的扭曲导致定转子接触界面的不均匀。这里不考虑转子的扭曲，仅考虑转子中心下沉对预紧力的影响。有限元计算过程为：假定初始状态下转子中心向下的位移约束为0.3 mm，然后施加静态加速度载荷，使得转子产生塑性变形；然后撤销加速度载荷，得到预紧力的大小；最后撤销对转子的位移约束，得到了转子中心由于塑性变形导致的下沉量为dc，如图6所示。通过多次计算，得到预紧力与下沉量dc之间的关系，如图7所示。显然预紧力随着下沉量的增加而减小，通过拟合得到了下沉量dc与预紧力的关系式

(1)

式中：ypre指的是预紧力。显然，想要预紧力恢复到初始值，可以在原先的基础上增加更多的垫片，通过有限元方法，得到了下沉量dc与预紧力恢复到初始状态(229.71 N)所需要的额外垫片厚度的关系，如图7所示，这里将额外垫片的厚度称为补偿量。对结果进行拟合，得到补偿量与下沉量dc的拟合关系式

(2)

式中:yc为补偿量。

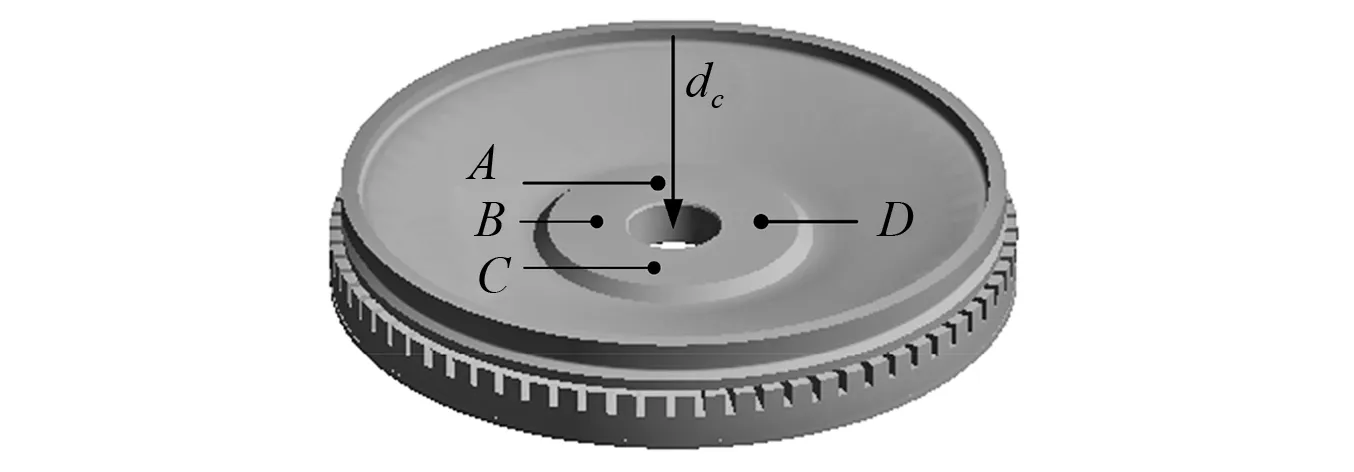
图6 转子变形示意图Fig.6 The diagram of rotor’s deformation

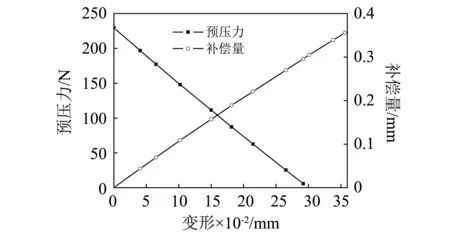
图7 转子中心下沉量与预紧力及补偿量之间的关系Fig.7 Relationship between sinkage between preload and compensation

2 超声电机的冲击实验

选取三个基本一致的超声电机(TRUM60)，利用马歇特捶对电机进行冲击实验，考察冲击载荷对超声电机性能的影响。整个实验平台如图8所示。图8(a)为冲击实验平台，主要由马歇特捶，加速度传感器与数据采集系统，其中超声电机固定在夹具内，冲击载荷的大小通过调整马歇特捶上棘轮的齿数来实现。图8(b)为电机性能测试平台，包括有超声电机驱动器，不接触激光测速仪以及充当重物的砝码等。

(a)冲击测试平台

(b)机械性能测试平台 图8 实验测试平台Fig.8 Experiment test platform

2.1 电机的机械性能测试与结果分析

将三个电机编号1，2，3, 并测得其在冲击前的机械性能，如图10所示。对三个电机进行冲击实验，冲击载荷分别为1 630 g，1 865 g与2 320 g。冲击过后。一号电机能够正常工作，但机械性能明显下降；二号电机能够正常工作，但是机械性能下降的更加明显，且在工作时有着沙沙的噪音；三号电机无法正常工作，输出轴松动，可以自由转动，说明预紧力机构失效。冲击过后的电机性能如图10所示。

根据1.2节的仿真结果可知，冲击对转子变形的影响主要分为两种：一种是转子中心的下沉;一种是转子的扭曲。为了验证转子是否产生了扭曲变形，在转子中心区域分别标记了四个不同位置的点A,B,C,D，如图6所示，对这四个点的下沉量分别进行测量。测量发现，在三个转子中，其A，B，C，D四个点的下沉量均有着±0.01 mm的波动，即转子中心区域不同位置的变形量不同， 说明冲击确实使得转子产生了轻微的扭曲变形。取四个点下沉量的平均值作为下沉量dc，如表2中所示。显然，转子中心的下沉量在冲击的作用下会下沉，且下沉量随着冲击幅值的增加而增加。测量结果证实1.2节中的仿真结果是正确的

将下沉量dc代入式(1)中，得到冲击过后的理论预紧力，计算结果显示三号电机的预紧力为0，这与实验结果相对应。为了恢复预紧力，可在原先的基础上增加补偿垫片，基于公式(2)计算得到了理论上所需要的补偿垫片的厚度，上述结果列于表2中。实验所用的补偿垫片如图9所示，厚度分为0.5 mm，0.2 mm，0.1 mm与0.05 mm。其中实际补偿时使用的垫片厚度不仅仅基于表2中理论计算的结果，还基于实际调试的过程，即通过增加不同厚度的垫片后进行不断调试，使得补偿后的电机表现出尽可能好的机械性能。不同电机的实际补偿的垫片厚度如表2所示。可以看出，1号电机的补偿垫片的厚度与理论结果十分接近，而2号与3号电机的补偿垫片的厚度与理论结果之间有着差距。可能的原因是二号与三号补偿厚度由多片补偿垫片组合而成，在使用时，多片垫片之间存在着间隙，使得补偿厚度在数值上有所减小。而电机在补偿后的机械性能如图10所示，可以看出电机的机械性能在补偿后得到了明显的回复，但是无法恢复到初始状态。可能的原因包括有冲击影响了定子的振动特性以及转子轻微扭曲变形导致的定转子不均匀接触进而电机机械性能的下降。

图9 补偿垫片Fig.9 Compensation gasket

图10 冲击过载对超声电机的机械性能的影响Fig.10 Performance of motors before and after impact and compensation

编号变形量 dc/mm预紧力/N理论补偿厚度/mm实际补偿厚度/mm10.1149.80.1060.120.273.40.2070.1530.5500.5230.45

2.2 定子的冲击测试

为了测试强度更高的定子的抗过载能力，将1号与2号电机进行幅值更高的冲击过载，幅值分别为9 718.3 g与3 582.6 g。冲击过后，两个电机均无法正常工作。除了转子之外，没有观察到明显的变形与损坏。利用了多普勒激光测振仪对两个定子的振动特性进行测试，结果如图11与12所示。从图中可以看出，一号定子与二号定子的振型仍然相对完整，二号定子的振型优于一号定子。其中两个定子均存在着波峰高度不一致的情况，在一号电机中，还存在由于波形不连续导致的振型畸变。这说明冲击载荷过大会引起定子振动特性的畸变。

通过对转子变形量的测试与分析和对定子的振动特性的测试，冲击载荷下引起电机性能变化的主要原因分为转子的变形所导致的预紧力降低与定子振动特性的畸变。其中，转子作为柔性元件，在较低的载荷下就会变形引起预紧力的降低甚至消失，从而引起电机的机械性能的下降。定子的抗过载能力更强，当冲击过载达到更大的幅值时，会引起振型的畸变。

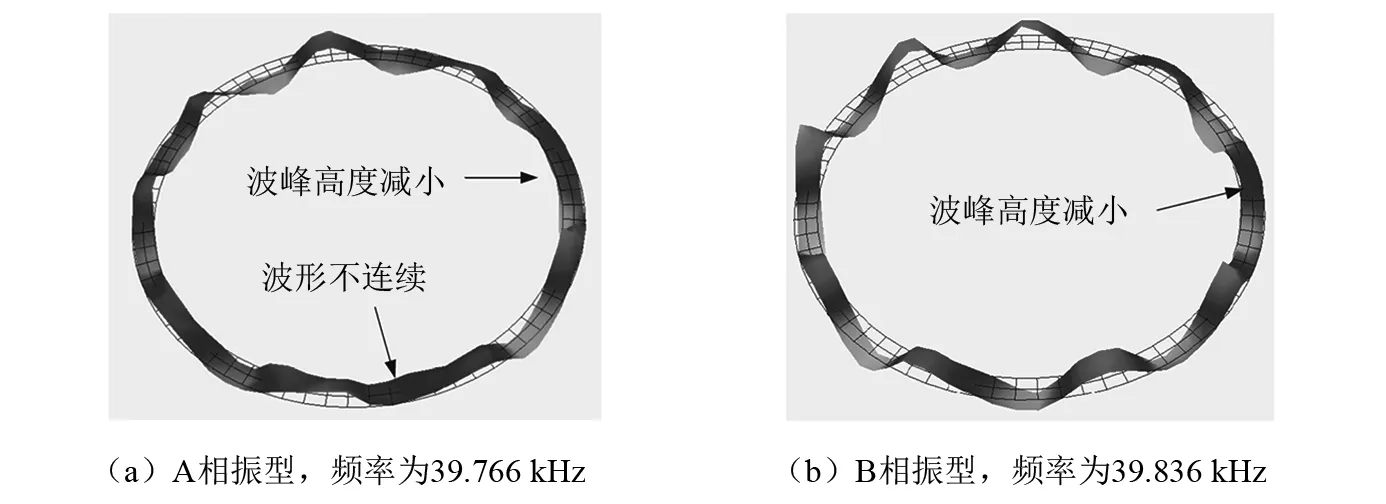
图11 定子1的振动特性Fig.11 Vibration characteristic of stator 1

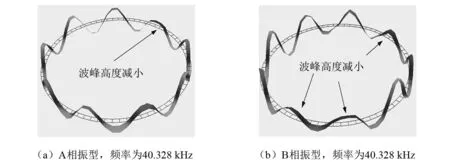
图12 定子2的振动特性Fig.12 Vibration characteristic of stator 2

2.3 橡胶的缓冲作用

橡胶，作为一种廉价的隔震缓冲材料，常用于各种结构器件在冲击条件下的防护。超声电机作为一种精密器件，也离不开缓冲隔震装置的保护，本节主要测试橡胶在冲击环境中对超声电机的保护作用。图13为电机未受到与受到橡胶保护的实物图。其中，橡胶厚度为2 mm，同样利用马歇特捶进行冲击实验，幅值分别为3 090 g，3 035 g与2 980 g。冲击前后的电机机械性能如图14所示。与图10中的结果对比，冲击后电机的机械性能损失较小，在可接受的范围内。这说明橡胶能够在冲击环境中对超声电机进行有效的保护。

图13 橡胶缓冲的实物对比图Fig.13 Physical comparison of rubber

图14 橡胶保护下的性能对比Fig.14 Performance comparison under rubber protection

3 结 论

本文建立了旋转型超声电机的有限元模型，得到不同冲击环境下超声电机的动态响应过程，并得到转子的变形量与预紧力之间的关系。通过实验测试了冲击载荷对超声电机机械特性与定子振动特性的影响，得到的结果如下：

仿真结果表明冲击对超声电机转子的影响主要分为两种：①转子的中心下沉变形；②转子的扭曲振动导致转子产生扭曲变形。这两种变形均通过实验测量得到验证。而定子的强度更大，不易在冲击环境中产生塑性变形。

不同的冲击环境对电机的变形将会产生不同的影响，冲击幅值越大，电机的变形越大，；当冲击载荷的脉宽接近结构的谐振频率时，结构的变形也越大。

理论分析与实验结果表明通过增加补偿垫片即可恢复预紧力，恢复超声电机的机械性能。但是实际测试发现电机的性能无法恢复到初始状态，其中原因可能有冲击影响了定子的振动特性以及转子轻微扭曲变形导致的定转子不均匀接触进而电机机械性能的下降。

定子的抗过载能力远远超过转子，但是当冲击幅值达到一定值，冲击载荷将会引起定子振动特性畸变，主要包括峰值高度的不一致以及振动波形的不连续。

橡胶作为一种缓冲隔震材料，能够在冲击环境中对电机进行有效的保护。