内置暗支撑钢筋混凝土剪力墙恢复力模型研究
2019-10-30王义俊张金轮
王义俊, 曹 兵, 张金轮
(安徽工程大学 建筑工程学院,安徽 芜湖 241000)
在地震作用下,钢筋混凝土材料的微观损伤表现为构件宏观上的抗震性能退化。已有的循环往复加载试验研究表明,构件性能的退化与其经历的最大位移和循环加载次数有关[1]。国外对恢复力模型研究始于材料这一层次上。早在19世纪末,德国学者Bauschinger通过对钢材的拉伸压缩试验,指出试验过程中产生的一个现象,即当钢材在一个方向加荷超过其弹性极限后,当再对其进行反向加荷时,其弹性极限将显著降低。此后钢材的这种现象就被称为“包辛格效应”。可以说,包辛格效应最先反映了钢材的恢复力模型。此后,Agrawl等[2]、Kent等[3]对钢筋的应力-应变特性进行了深入的研究,提出了考虑钢筋硬化和包辛格效应的应力-应变模型,并将其应用于钢筋混凝土构件。
在20世纪末,国内学者对钢筋混凝土构件的恢复力模型进行了大量试验研究[4-8],这些研究多集中于柱的恢复力模型进行的研究,而对钢筋混凝土剪力墙的恢复力模型研究则涉及较少。郭子雄等[9]通过对10片带框开洞低矮剪力试验结果,提出了低矮剪力墙的恢复力模型;李宏男等[10]在9片剪力墙试验的基础上提出了钢筋混凝土剪力墙的恢复力模型;李晓蕾等[11]在12片剪力墙试验的基础上,用最小二乘法拟合建立了钢筋混凝土剪力墙四折线骨架曲线。然而,上述剪力墙恢复力模型都是基于普通剪力墙试验数据而得到的,对于带暗支撑剪力墙恢复力模型较少涉及。
本文是在对内置暗支撑试验拟静力试验的基础上,通过理论分析并结合带暗支撑剪力墙的试验数据,确定了内置暗支撑剪力墙恢复力模型各参数的取值及滞回规则,并与试验所得到的滞回曲线进行了对比分析。同时,通过大量数据拟合,得到了内置暗支撑剪力墙的刚度退化规律,并给出计算公式。
1 试验概况
1.1 试件设计
试验共设计了6片内置暗支撑剪力墙试件,截面尺寸为700 mm×100 mm,试件高1 400 mm和1 050 mm,剪跨比分别为2.0和1.5,模型缩尺比例为1∶3。试件HSW由普通混凝土浇筑,试件HDHSW1、HDHSW2和HDHSW3均由高阻尼混凝土材料浇筑[12];试件PHDHSW与试件PHDECCSW底部1/4高度分别浇筑高阻尼混凝土和高阻尼ECC(Engineered Cementitious Composites)材料,剪力墙上部3/4高度范围内均用普通混凝土浇筑[13]。剪力墙试件尺寸与配筋,见图1所示。
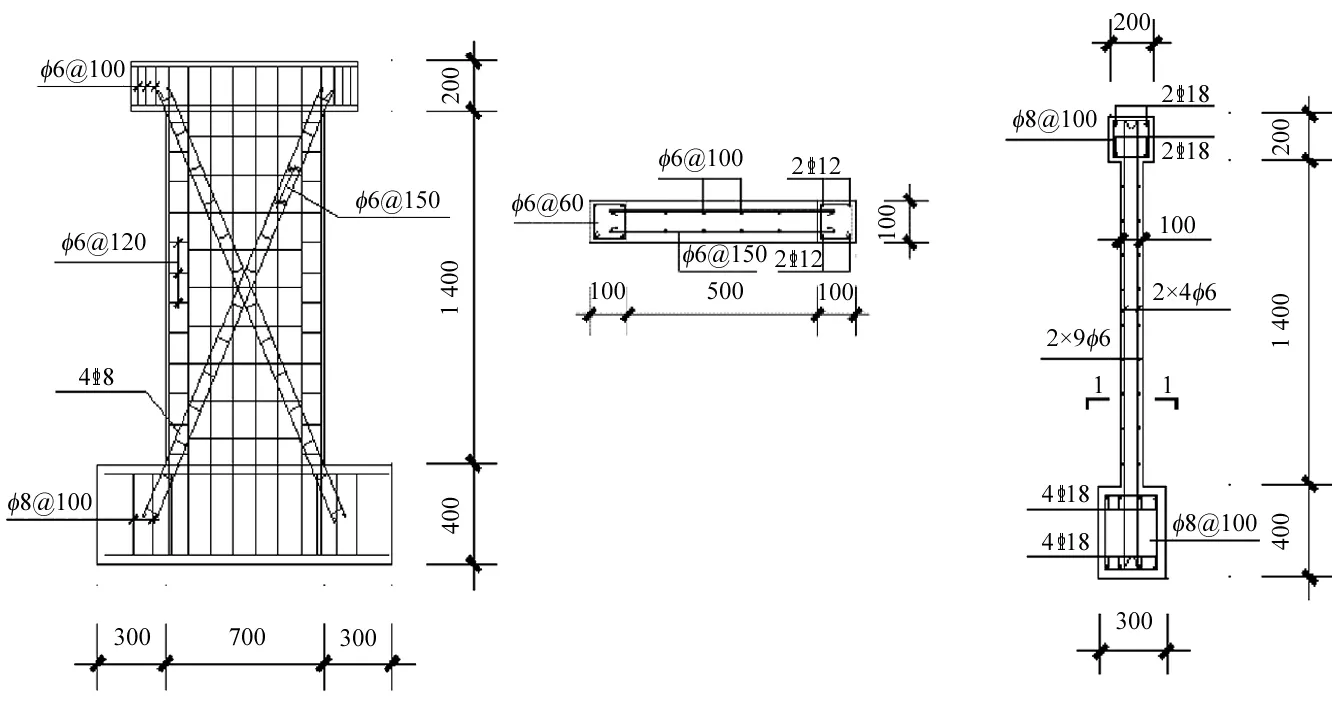
图1 带暗支撑剪力墙截面示意图Fig.1 Dimensions and steel reinforcement of specimens
试验主要变化参数为混凝土类型、轴压比和剪跨比,其主要设计参数如表1所示。从表1可知,剪力墙试件的试验轴压比为在0.1~0.4,主要是为了更好地考察轴压比对特征荷载及特征刚度的影响。在试件加载梁顶部和端部分别施加竖向荷载和低周水平往复荷载,用以研究剪力墙的抗震性能。

表1 内置暗支撑剪力墙构件主要设计参数Tab.1 Design parameters of shear walls with concealed bracings
1.2 骨架曲线
通过低周期往复加载试验可得到剪力墙试件的荷载-位移滞回曲线的外包络线,即为骨架曲线。结构或构件的抗震性能可通过骨架曲线进行定量的衡量,如极限承载力和延性特征[14]。
2 内置暗支撑剪力墙恢复力模型分析
2.1 骨架曲线恢复力模型
通过对中高剪力墙的骨架曲线进行对比分析,可发现骨架曲线先后经历了开裂点、屈服点、峰值点和极限点,直至试件破坏。现有对中高剪力墙骨架曲线的研究一般有刚度退化的三折线模型[15]和四折线模型[16]两种。由于骨架曲线的四个特征点与结构构件的充分运行阶段(OP)、基本运行阶段(IO)、生命安全阶段(LS)和接近倒塌阶段(CP)四个性能点[17]具有一一对应的关系。基于此,本文采用四折线模型,并通过理论分析的方法来确定上述特征点的荷载及与其相对应的位移,并通过上述参数进而确定恢复力模型的特征点, 见图2所示。图2中,C点为开裂点;Y点为屈服点,可用能量等值法确定;M点为峰值点;U点为极限点,按荷载下降到峰值荷载的85%时对应的位移确定。
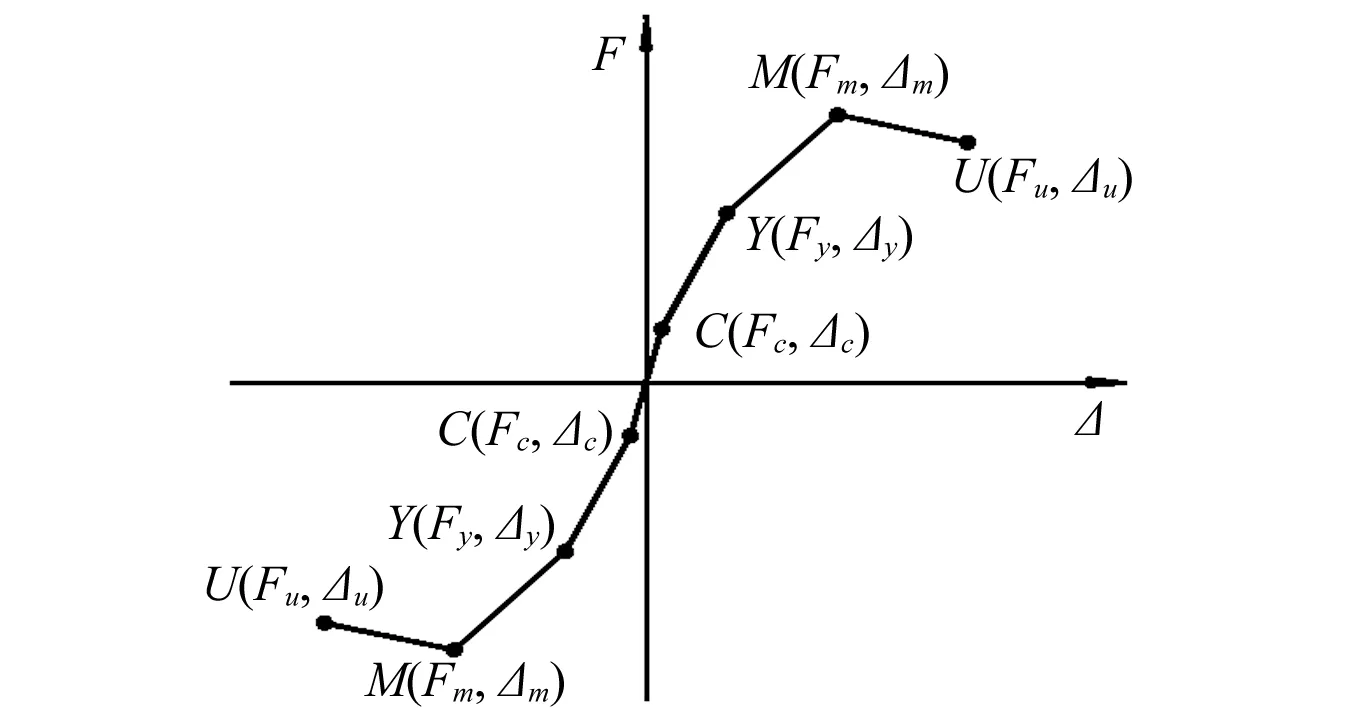
图2 剪力墙四折线恢复力模型Fig.2 Four-fold resilience model of shear wall
2.2 特征荷载值计算
对钢筋混凝土剪力墙进行加载试验时,一般可以简化为悬臂梁顶端作用下的水平集中力。鉴于本文采用的是四折线恢复力模型,需要计算剪力墙在开裂点、屈服点、峰值点和极限相应的荷载。在进行分析计算时,采用如下假定:①平截面假定,即截面变形后仍然保持平面状态,且应变沿截面高度呈线性分布;②不考虑钢筋与混凝土之间的粘结滑移,认为两者之间能够协调变形;③在混凝土开裂前,受拉区混凝土能够完全参与工作,不考虑受压区钢筋的有利作用。
剪力墙截面达到屈服时,受拉区混凝土大部分已经退出工作。因此,在计算开裂荷载时,考虑混凝土的受拉作用,而在计算屈服荷载、峰值荷载和极限荷载时均不考虑混凝土的受拉作用。
2.2.1 开裂荷载的计算
钢筋混凝土剪力墙在初始加载时,其截面产生的弯矩很小,应变沿截面高度范围内呈线性变化,试件基本处于完全弹性阶段,应力和应变成正比关系。随着水平荷载的进一步增加,试件底部截面弯矩逐渐增大,应力和应变也随之增大。当水平荷载达到开裂荷载Mc时,剪力墙底部恰好达到开裂弯距Fc,相应混凝土受拉边缘达到开裂应变εc。此时,剪力墙受拉和受压区应力沿截面高度方向线性关系。剪力墙截面开裂状态截面应力应变分布图,如图3所示。
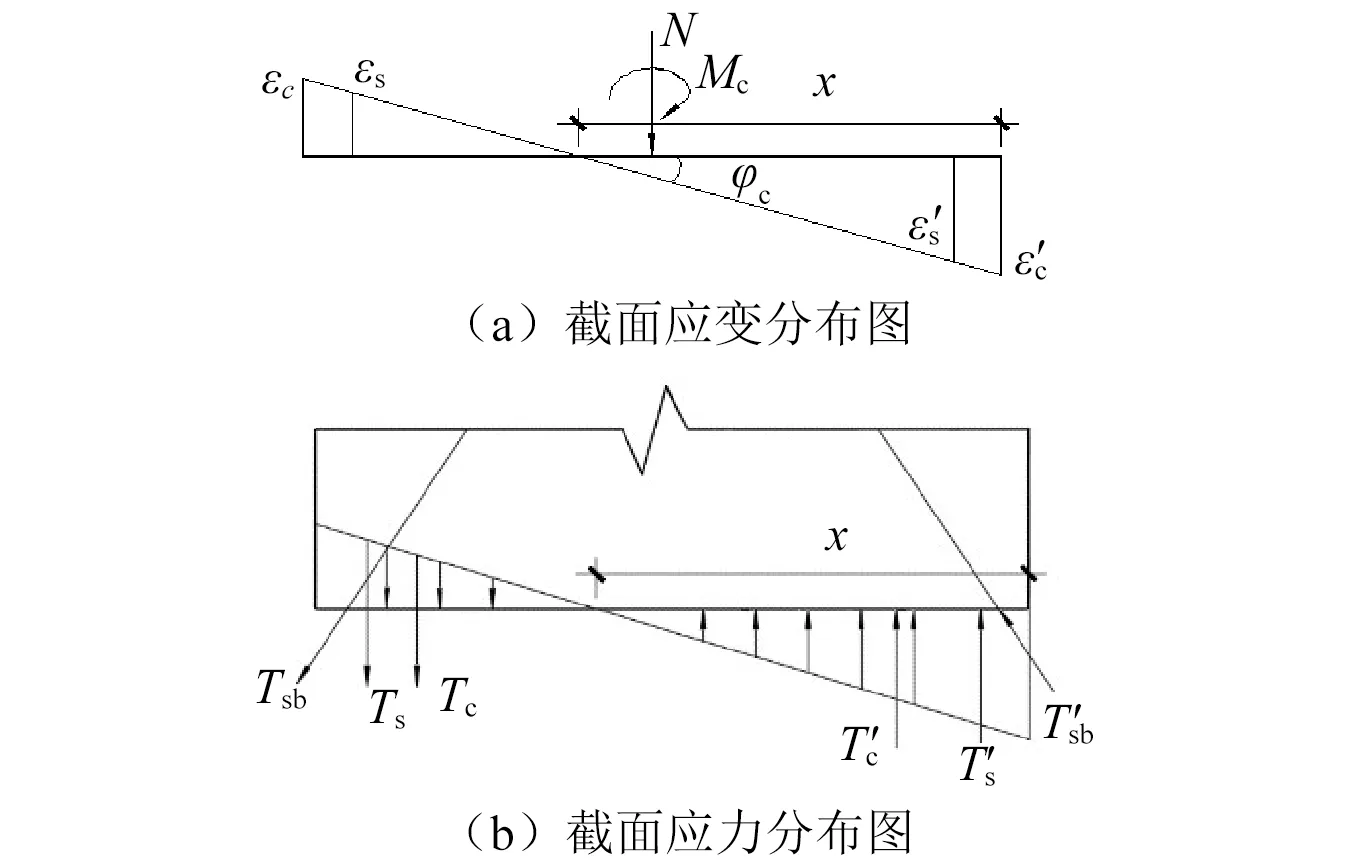
图3 开裂状态截面应力应变分布图Fig.3 Stress and strain distribution of cracking cross-section
当剪力墙达到开裂状态时,截面的开裂曲率φc可表示为:
(1)
由平截面假定和式(1),可得到暗柱与暗支撑钢筋和暗支撑钢筋分别在受拉与受压区的钢筋应变以及混凝土和钢筋的抗力,即:
N+Ts+Tsbsina+Tsw+Tc=T′s+T′sbsina+T′sw+T′c
(2)
式中:εs=(hw0-x)φc,ε′s=(x-a′s)φc
εsb=(hw-x-asb)φc,ε′sb=(x-a′sb)φc
Tsw=0.5ρwbw(hw0-x)Esεsw
T′sw=0.5ρwbw(hw0-a′s)-Esεsw
Tc=0.5bw(hw-x)Ecεc
T′c=0.5bwxEcε′c
式中:N为剪力墙截面所受轴向压力;T和T′分别为墙肢受拉和受压区所受合力;ε和ε′为钢筋或混凝土在受拉和受压应变;A和A′分别为钢筋在受拉和受压区面积;a和a′分别为受拉和受压区钢筋合力点到截面边缘的距离;hw0为剪力墙截面有效高度;hw为剪力墙截面高度;x为剪力墙受压区高度;ρw为剪力墙竖向分布筋配筋率;α为暗支撑水方向倾角;E为钢筋或混凝土弹性模量。上述符号下标s、c、sb和sw分别表示暗柱钢筋、混凝土、暗支撑钢筋和分布纵筋;
由式(1)及式(2),可求解得到截面受压区高度值x和截面开裂曲率值φc。由截面的弯矩平衡关系,通过对截面形心轴取矩,可得到剪力墙开裂弯矩和开裂水平荷载,即:
Mc=Tsb(0.5hw-asb)sinα+Tsw(0.5hw+x-2as)/3+
Ts(0.5h-as)+Tc(0.5hw+x)/3+T′s(0.5h-a′s)+
T′sb(0.5hw-a′sb)sinα+T′sw(0.5hw-x-2a′s)/3+
T′c(0.5hw-x/3)
(3)
(4)
式中:Hw为剪力墙加载梁中部至基础顶面的距离。
2.2.2 屈服荷载的计算
剪力墙开裂后将进入带裂缝工作阶段,继续加载时,其所承受水平荷载逐渐增加。当剪力墙截面受拉区纵向受拉钢筋达到屈服应变时,受拉区大部分混凝土已出现拉裂裂缝,可以认为受拉区的混凝土已退出工作。因此,在计算屈服荷载时,忽略受拉区混凝土的承担拉力作用;在受压区,混凝土开始出现塑性变形。为简化计算,假定受压区混凝土的应变沿截面高度仍为线性分布。剪力墙屈服状态截面应力应变分布图,如图4所示。

图4 屈服状态截面应力应变分布图Fig.4 Stress and strain distribution of yielding cross-section
剪力墙达到屈服状态时,截面屈服曲率φy可表示为:
(5)
由平截面假定和式(5),可得暗柱与暗支撑钢筋分别在受拉与受压区的钢筋应变及混凝土和钢筋的抗力,即:
N+Ts+Tsbsinα+Tsw=T′s
(6)
εs=(hw0-x)φy,εsb=(hw-x-asb)φyε′c=xφy
由式(5)及式(6),可求解得到截面受压区高度x值和截面屈服曲率值φy。由截面的弯矩平衡关系,通过对截面形心轴取矩,可得到剪力墙屈服弯矩和屈服水平荷载,即
My=Tsb(0.5hw-asb)sinα+Ty(0.5h-as)+
Tsw(0.5hw+x-2as)/3+T′c(0.5hw-x/3)
(7)
(8)
2.2.3 峰值荷载的计算
当纵向受力钢筋超过其屈服状态以后,继续增加水平荷载时,受压区混凝土的应变逐渐增大。当受压区混凝土达到其峰值压应变时,约束边缘构件内的混凝土由于箍筋的约束作用其压应变将继续增大,直至达到约束混凝土峰值压应变,约束混凝土采用Saatcioglu等[18]提出的本构,其约束混凝土极限压应变计算如式(9)~式(11)所示:
εcu=260ρε1+ε85%
(9)
(10)
(11)
式中:ρ为约束混凝土范围内箍筋配箍率;Asc为箍筋两个方向总面积;s为箍筋间距;bcx和bcy分别为约束区混凝土的两个方向长度;ε1和εc0分别为约束混凝土与普通混凝土峰值应变,εc0一般取0.001 8,fcc与fc0为与之相应的峰值应力ε85%; 为普通混凝土应力-应变曲线下降段达到最大应力85%时的应变,即为普混凝土的极限压应变,一般取0.003 3。
根据试验结果,当剪力墙达到峰值荷载时,受拉区混凝土纵向钢筋和暗支撑钢筋均已达到屈服状态峰值状态下的截面应变应力分布图,如图5所示。
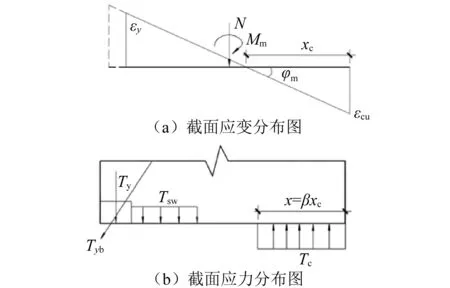
图5 峰值状态截面应力应变分布图Fig.5 Stress and strain distribution of peaking cross-section
剪力墙达到峰值状态时,截面的峰值曲率φm可表示为:
(12)
式中:x为计算受压区高度,可用等效矩形应力图来代替实际混凝土受压应力图,取x=βxc,其中,β为矩形应力图受压区高度与中和轴高度的比值。
根据竖向外力与抗力相等可得:
N+Ty+Tybsinα+Tsw=T′c
(13)
式中:
Ty=EsεyAsTyb=EsεybAsbTsw=0.5ρwbw(hw0-x)EsεswTc=0.5bwxEcεcu
由式(12)及式(13),根据截面的弯矩平衡关系,可得到剪力墙峰值弯矩和峰值水平荷载,即:
Mm=Tyb(0.5hw-asb)sinα+Ty(0.5h-as)+
Tsw(0.5hw+x-2as)/3+T′c(0.5hw-x/3)
(14)
(15)
2.2.4 极限荷载的确定
根据内置暗支撑单肢剪力墙的试验结果,极限荷载Fu达到峰值荷载的85%时,内置暗支撑剪力墙已发生破坏,即:
Fu=0.85Fm
(16)
2.3 特征刚度计算
剪力墙特征刚度包括初始刚度、开裂刚度、屈服刚度和极限刚度。在加载初期,剪力墙处于完全弹性阶段。根据材料力学的公式可得到剪力墙的初始刚度K0,即:
(17)
式中:Gc混凝土剪切模量,取Gc=0.4Ec;I为剪力墙截面惯性矩;μ为剪应力不均匀系数;对矩形截面一般取1.2;A为剪力墙截面面积。
由式(17)计算所得的内置暗支撑剪力墙的初始刚度与实测值进行比较,如表2所示。
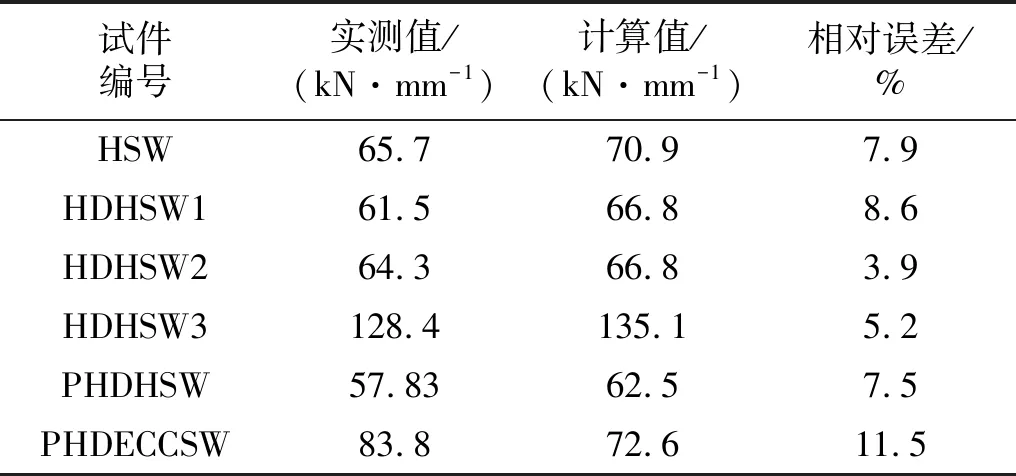
表2 内置暗支撑剪力墙初始刚度实测值与计算值Tab.2 Measured and calculated value of shear walls with bracings
对内置暗支撑剪力墙试验数据进行统计分析,剪力墙的开裂刚度Kc=0.33K0;屈服刚度Ky=0.24K0;峰值刚度Km=0.11K0;下降段刚度Ku=0.06K0。
2.4 特征位移的计算
在计算出剪力墙相应的特征荷载和特征刚度后,结合图2所示的骨架曲线,可进一步计算出剪力墙的开裂位移Δc、屈服位移Δy、峰值位移Δm和极限位移Δu,即:
(18)
(19)
(20)
(21)
3 滞回规律
3.1 卸载刚度
对试验所得到滞回曲线进行研究可发现,在试件产生初始裂缝以前,可认为试件处于弹性阶段,卸载刚度可取开裂刚度Kc;当继续加载至试件屈服荷载时,试件的刚度逐渐减小,滞回曲线呈现出较为明显的捏缩形状;当荷载超过屈服荷载后,剪力墙试件的刚度逐渐降低,此时滞回曲线呈现出捏缩程度逐渐增大,这说明了试件的卸载刚度有显著的降低。观察内置暗支撑剪力墙循环加载滞回曲线可知,屈服荷载后,随着剪力墙水平位移的逐渐增加,试件的刚度呈现出不断退化的现象。这意味着,剪力墙水平位移的变化是其刚度退化的宏观结果。
基于此,对内置暗支撑单肢剪力墙试验滞回曲线各滞回环顶点处的卸载刚度与屈服刚度的比值与加载位移比值进行了统计,利用MATLAB软件进行了相应参数下具有95%保证率的关系曲线拟合,并在图中给出了拟合曲线的相关系数(R)、均方差(RSME)和残差平方和(SSE) 如图6所示。通过数据的回归拟合,得到了内置暗支撑剪力墙试件卸载刚度Kun,即:

图6 剪力墙刚度退化曲线Fig.6 Stiffness degradation curve of shear wall
Kun/Ky=1.2 exp(-0.5Δj/Δy)+0.25
(22)
3.2 加卸载规则
加卸载规则是剪力墙恢复力模型的重要组成部分,能综合反映剪力墙的强度、刚度退化和捏缩效应等基本的规律。当水平荷载低于开裂荷载时,试件处于弹性阶段,卸载时不考虑剪力墙的残余变形和刚度退化;当继续加大水平荷载时,试件处于弹塑性状态,卸载时剪力墙有一定的残余变形和刚度退化,按式(19)计算出卸载刚度。结合现有的恢复力模型的研究成果与本文采用的恢复力模型加卸载规则,如图7所示。其加卸载规则如下:①剪力墙开裂前,加载刚度取开裂刚度Kc,加载路径指向开裂点1;卸载至零点并反向加载时,按弹性加载,通过原点指向开裂点1。②当剪力墙开裂后且未达到屈服荷载前,加载刚度取屈服刚度Ky,加路径指向屈服点2;卸载至零点(路径2~9)后,反向加载时指向开裂点5。③当剪力墙屈服后且未达到峰值荷载前,加载刚度取屈服刚度Km,加路径指向峰值点3;卸载至零点(路径3~11)后,反向加载时指向屈服点6。④当剪力墙水平荷载超过峰值荷载时,加载刚度取下降段刚度Ku,加路径指向极限点4;卸载至零点(路径4~13)后,反向加载时指向极限点8。⑤当施加的水平荷载下降到峰值荷载的85%时,即认为达到了剪力墙恢复力模型的极限位移。在加载过程中,若所施加的水平荷载低于特征点荷载或位移时,则恢复力模型加载过程按照上次加载过程继续进行。
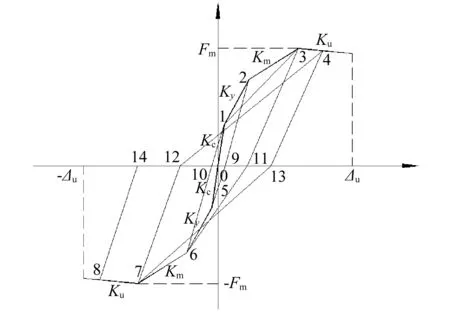
图7 剪力墙恢复力模行走路径Fig.7 Restoring walk path of shear wall
4 恢复力模型验证
为验证本文提出的内置暗支撑钢筋混凝土剪力墙恢复力模型的有效性,对选自文献[12]及文献[13]中的剪力墙进行验证分析。图8为计算滞回曲线与试验所得滞回曲线的对比。从图8可知,计算滞回曲线与试验滞回曲线吻合情况较好,能较好的反映实测滞回曲线走向及捏缩现象。
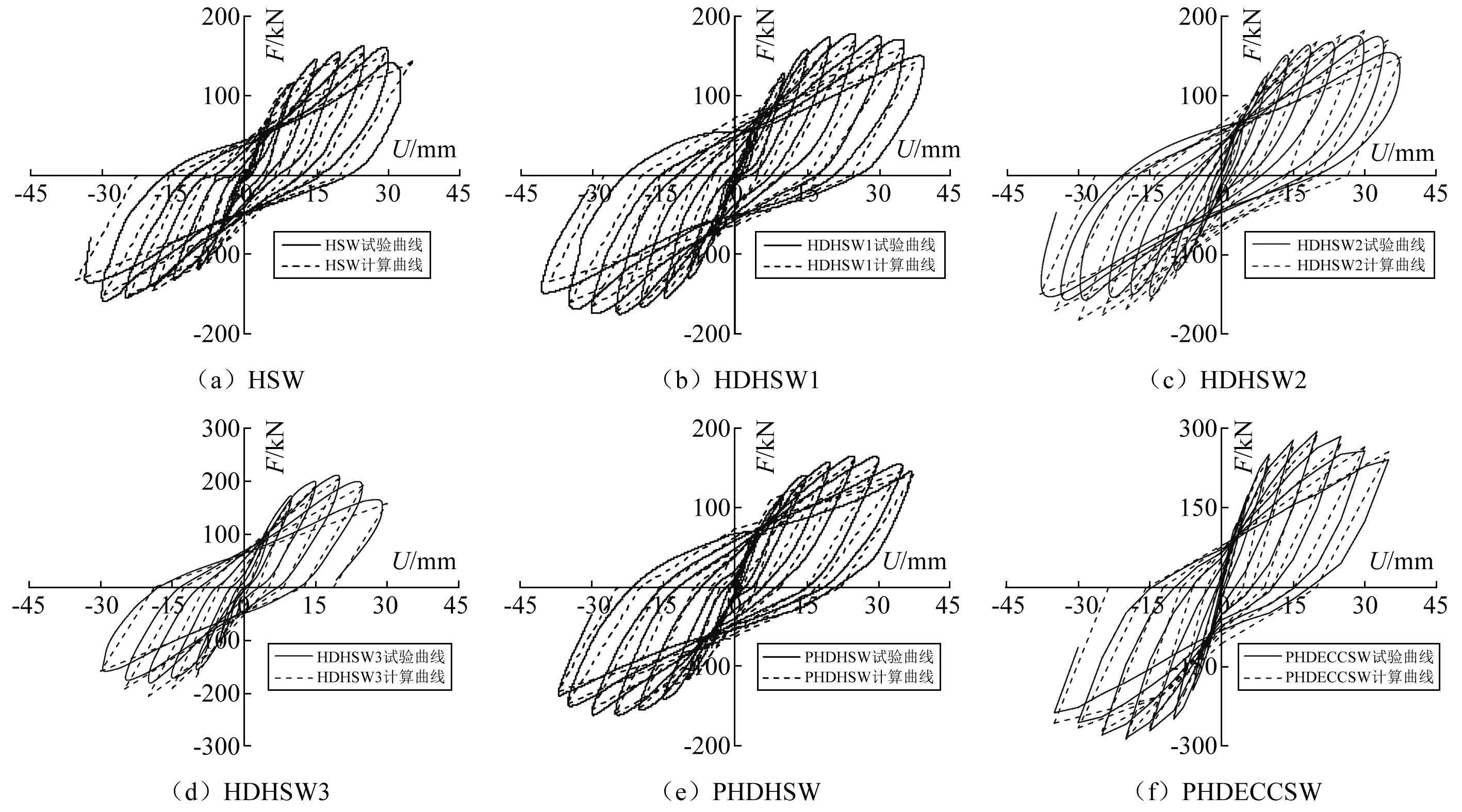
图8 恢复力模型计算和试验曲线的对比Fig.8 Comparison of restoring force model and test curves
5 结 论
(1) 在试验所获得的骨架曲线的基础上,通过统计分析,建立了适合于内置暗支撑剪力墙的四折线恢复力模型,并给出了骨架曲线上各关键点的计算公式。
(2)利用MATALAB软件,进行了基于刚度退化数据的回归分析,得到了内置暗支撑剪力墙的刚度退化公式。研究结果表明,剪力墙水平位移的变化是其刚度退化的宏观结果,其水平位移主要与内置暗支撑剪力墙的剪跨比、轴压比等因素有关。在此基础上,提出了内置暗支撑剪力墙的恢复力行走路径。
(3)本文所提出的恢复力模型能较好地反映试件的抗震性能, 为内置暗支撑剪力墙结构进行弹塑性地震反应分析奠定了理论基础,具有一定的合理性。需要注意的是,本文所得到的结论主要是针对剪力墙试验进行模拟分析,在使用中需要考虑剪力墙的实际工作状态,如何将结论应用到实际工程分析,有待于进一步深入地研究。
