基于分层模型的功能梯度输流管道耦合振动

朱竑祯， 王纬波， 殷学文， 高存法

(1.南京航空航天大学 航空学院 机械结构力学及控制国家重点实验室，南京 210016；2.中国船舶科学研究中心 船舶振动噪声重点实验室，江苏 无锡 214082)

功能梯度材料(Functionally Graded Material, FGM)的概念最早由日本科学家于1984年提出[1]，是指材料属性随空间位置呈连续梯度变化的新型复合材料。随着材料制备工艺的精进，功能梯度材料目前已经在耐磨损[2]、缓解内部热应力及抗断裂[3]等应用中展现出传统材料难以超越的独有优势。针对不同的使用需求，功能梯度材料具有很强的可设计性，因此在未来工业及工程领域具有极大的潜在应用前景。

输流管道作为一种介质运输方式，广泛应用于水利、化工、航空及海洋工程等领域中。传统管道一般采用金属材料，例如潜艇中布置了大量的金属管道承载各种低速液体的流动，包括海水以及各种机器运转产生的废水等。经过时间的积累，金属极易受到这些液体的腐蚀，从而造成金属管道内部的堵塞，因此常常需要斥巨资用于管道的防腐蚀处理和定期维护以保证其使用年限[4]。此外传统的金属材料声学阻尼性能差，流体与管壁相互碰撞挤压不仅引起耦合振动，增大噪声，甚至还可能导致管道的疲劳破坏。新型复合材料具有优良的抗疲劳、阻尼特性以及很强的设计性，为工业设计引入新风，受到广泛关注[5]。目前已有许多国外学者研究用新型复合材料制作水下螺旋桨，既耐腐蚀，且预期能比传统材料有更好的声学性能[6-8]。但一般复合材料层间剪切强度和拉伸强度低[9]，而且极易产生分层损坏从而导致复合材料的失效。而功能梯度材料则由于其材料特性连续变化，材料组份之间无显著界面，因此与传统材料和复合材料相比在优化应力分布方面有明显的优势。船舶管道系统的可靠性直接影响了其内部各仪器的正常运作与配合，因而本文考虑用功能梯度材料这种新型材料取代传统金属材料和复合材料用于输流管道。

在工程中，相对截面尺寸而言，一般管道长度较大，因此多采用梁模型描述管道的振动。早期的理论中大多将内部流体视为附加质量，将流速和压力视为常量，忽略流体与管道的耦合效果[10-12]，对于输送液体的管道的描述是不精确的[13]。随耦合理论的深入发展，William[14]和Walker等[15]考虑了流体在轴向的可压缩性，Wiggert等[16]和Lesmez等[17]计入管道的泊松耦合效应影响，Lee等[18]分析了重力作用和流体的黏性，Gorman等[19]引入了管道的径向变形和初始预应力，传统材料输流管道的振动理论已经发展得较为成熟。尽管对于功能梯度材料的理论研究不少，但大多仅限于纯结构的研究，如功能梯度梁[20-22]、功能梯度板的数值分析等[23-25]，而目前对于功能梯度输流管道方面的研究主要通过圆柱壳[26]、Euler梁[27-34]或Timoshenko梁[35]模型研究管内流速导致管道失稳的问题。圆柱壳的模型虽然从三维角度分析管道更详细准确，但是难以模拟复杂的组装管道。而Euler梁模型忽略了截面的剪切变形，只能适用于薄壁细长管道，难以满足工程各类计算需求。此外在处理管道失稳问题中，一般只考虑管道的横向方程，对于流体的处理是较为简单的，未考虑流体在轴向的可压缩性，甚至只将流体视为附加质量。而实际上对于管道这种链式结构来说，其轴向和流体的运动影响了管道上下游振动与声的传递特性。为了分析功能梯度管道对于管道结构和流体的影响，将流速和压力设为变量，计入流体在管道轴向的可压缩性，基于Timoshenko梁模型，综合考虑了功能梯度材料管壁与流体的相互作用，通过Hamilton原理及流体动量、连续方程得出功能梯度输流管道的耦合振动方程。

功能梯度管道的材料属性沿厚度方向变化，本文采用离散模型来描述，将管壁均匀划分若干层，每一层近似为均匀材料，以此模拟连续梯度变化。动刚度法是基于单位内控制方程的精确解，与有限元法相比具有较高的计算效率[36]，因此本文利用动刚度法进行数值求解，然后通过算例分析了梯度指数的变化对于结构模态、流体模态及时域响应的影响，为将来功能梯度材料的工程应用提供一定理论依据。

1 输流管道振动方程

1.1 管道运动方程

本文计算的输流管道为圆形截面，管道径向坐标记为r，截面内半径为r1，外半径为r2。材料参数如杨氏模量、密度及泊松比均沿半径呈幂律变化[37]。

式中：Q(r)表示沿厚度方向呈连续梯度变化的材料参数，包括了杨氏模量E，密度ρ和泊松比μ等。下标1和2分别表示内界面和外界面的材料参数，n为梯度指数，表征材料的体积分布规律。

本文采用层合近似模型[38-40]，将这种连续梯度变化的功能梯度材料视为由多层连续梯度材料叠加成的层合材料。如图1所示，沿厚度方向把截面均匀划分为K层，每一层视为均匀材料，以此近似模拟沿半径方向变化的材料属性。对于第m层，该层的材料参数取为中间位置的值，记为Qm，写为如下的函数形式：

(1)

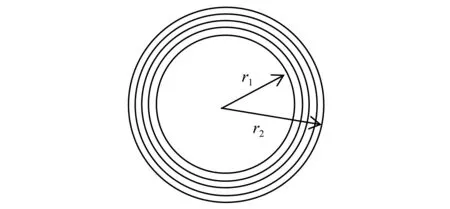
图1 管道截面径向分层模型Fig.1 Multi-layered model on the cross section of pipe

式中：rm1和rm2分别为第m层的内外半径。当需要考虑阻尼的影响时，可用复弹性模量E(1+iη)代替原弹性模量，其中η=2ξ，ξ为阻尼比，i为虚数单位。

工程上一般采用梁模型来描述管道，在Timoshenko梁模型中需考虑梁的剪切变形。以x和z方向分别表示管道的轴向和横向，对于梁上任意一点，轴向位移和横向位移表示为：

(2)

式中：u和w表示梁的中心面(z=0)的位移，φ(x,t)为截面的法线转角，t为时间。由几何方程可得应变为：

(3)

式中：微分符号(′)=∂/∂x。

由本构方程，应力表示为：

(4)

将应力式(4)在面内积分即可得到横截面上的轴力、弯矩和剪力：

(5)

在图2中，管道与水平面的倾斜角为θ，则重力加速度在轴向和横向的分量分别为gx=gsin(θ)和gz=gcos(θ)。管内流体对于管壁的单位长度垂直作用力和切向作用力分别为Nf和τ。

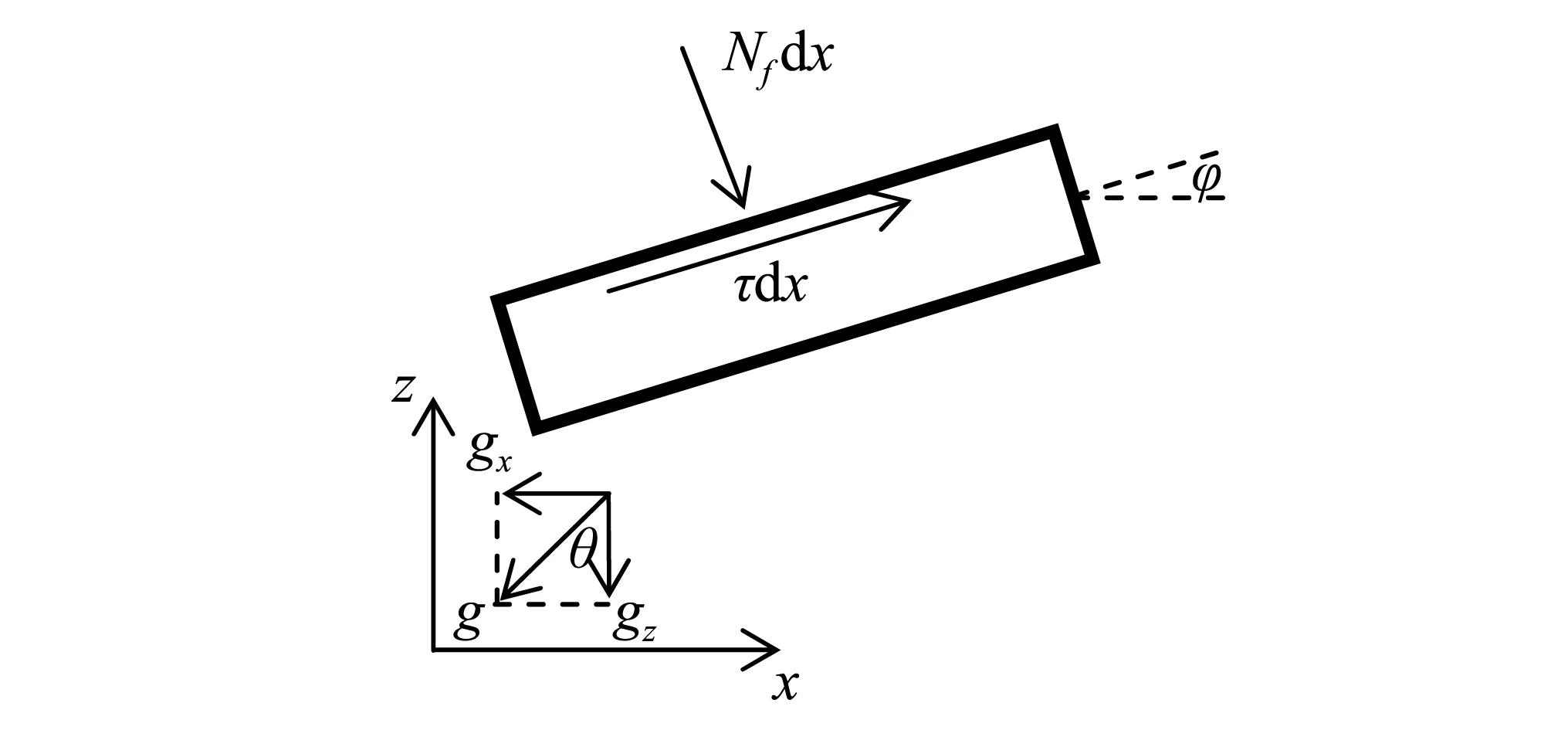
图2 管道微段局部坐标系Fig.2 Local coordinate system of an infinitesimal pipe element.

根据Hamilton原理，对系统泛函取极值：

(6)

式中：T为动能，U为应变能，W为非保守力做功，其具体形式为：

(7)

将式(6)代入式(7)中可得管道运动方程为：

(8)

1.2 流体方程

管道内流体的动量方程与管壁结构无关，可参考已有的管道理论，表示为：

(9)

式中：p为流体压力，Af为流体截面积(对于充液管道而言，即为内径面积)，c为流速，mw为单位长度流体的质量，微分符号为(·)=∂/∂t，(′)=∂/∂x。

根据流体力学[41]，流体与管壁间的摩擦作用力为：

(10)

此外，管道内流体的连续方程为：

(11)

式中：ρw为管道内流体的密度，根据流体状态方程有：

(12)

式中：Ev为流体的体积模量。

由于流体对于管壁的挤压而造成面积的变化，此外由于泊松比的效应，轴向的应变也会引起横向变形。因此，式中的第二项为[42]：

(13)

式中：ε2为横向应变，ε1为轴向应变，μ为泊松比，由于泊松比数值较小，影响相对小，因此在该式中取为截面的平均泊松比。

式(13)中的轴向应变为ε1=u′。图3为圆环截面的受力图，其中F为内力，p为内流体对于管壁的压力，根据受力平衡得：

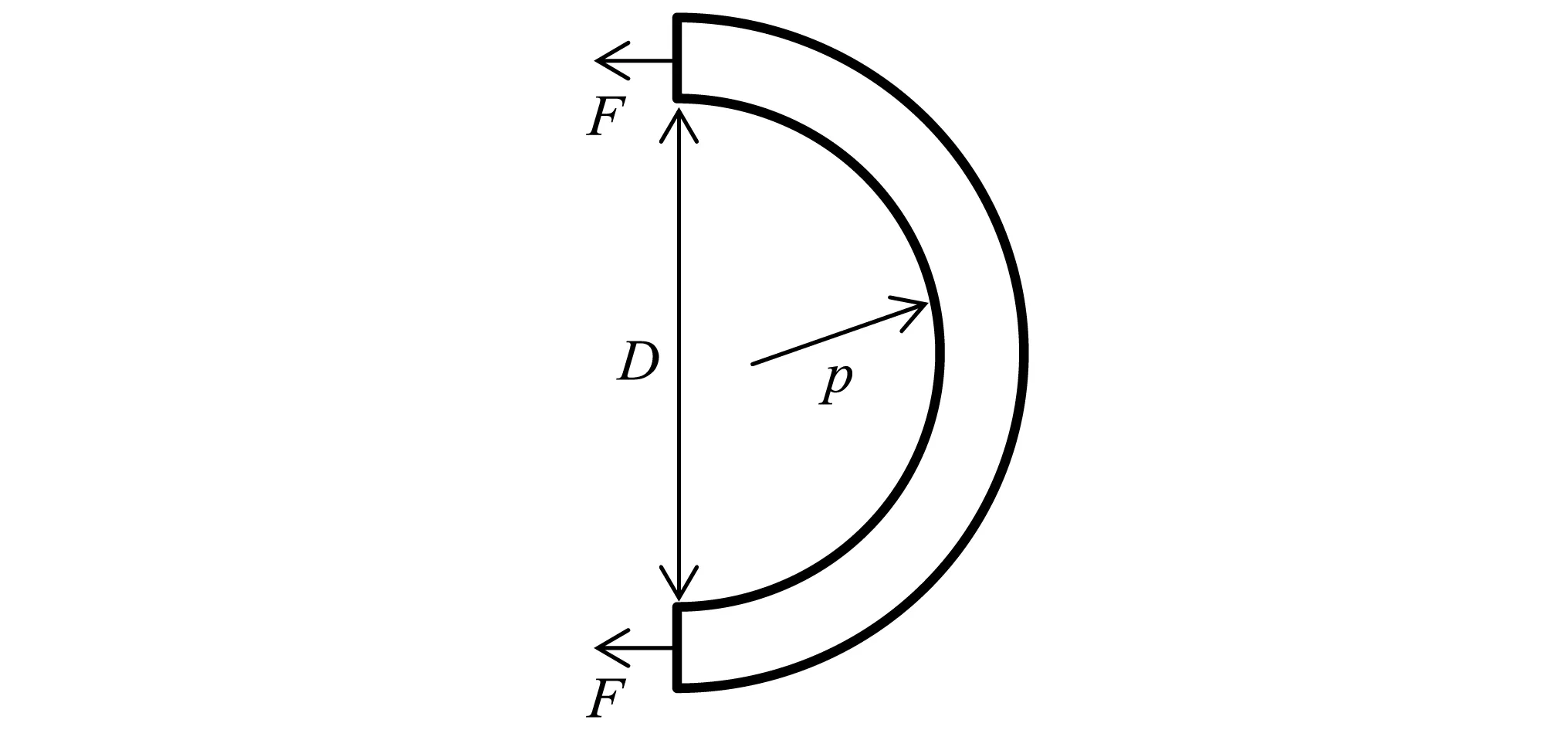
图3 圆环截面受力示意图Fig.3 Force diagram of annular section.

因此连续方程化为：

(14)

2 输流管道振动方程求解

为了对方程组进行简化，将流速和流体压力线性化，表示为：

c(x,t)=c0+cd(x,t),p(x,t)=p0+pd(x,t)

式中：c0和p0表示稳态时的定常流速和定常压力，而cd和pd表示微小的扰动变量。

当管内流体在高速高压下方程中的非线性项对结构的动态响应才有明显的影响[43]，在此我们主要考虑工程中的低速流动情况。因此为便于方程的求解，略去非线性项，由流体方程(9)得到Nfφ=mwgzφ。此外由于扰动变量远小于常量即cd≪c0，pd≪0，舍去扰动项的高次项，从而消去管道方程式(8)中管壁与流体的相互作用力，结合连续方程式(14)可得功能梯度输流管道的耦合振动方程组为：

(15)

将式前四个方程写为矩阵形式：

MΦ=0

式中：Φ=[uwφcd]T，M为微分系数矩阵。

注意到|M|为关于x的八次微分方程，因此将位移未知量设为如下形式：

对于|M|=0求解，可得到八个根，记为λ1～λ8。假设横向位移函数形式为：

式中：i为虚数单位(i2=-1)，ω为圆频率。根据方程(15)，其他三个变量与横向位移的关系为：

式中：C1～C8为常系数，fj，huj，hcj可由方程系数求得，在此不作赘述。然后将轴向位移和流速函数代入式(15)最后一个方程中，可求得压力变量。

对于一根长为L的管道，将其首末两端作为单元节点，位移向量写为：

d=[u(0)w(0)φ(0)cd(0)u(L)w(L)φ(L)cd(L)]T

相应的节点力向量写为：

f=[N(0)Q(0)W(0)pd(0)N(L)Q(L)W(L)pd(L)]T

显然内力及压力函数都可由位移表示，因此节点位移和节点力都可以写成关于常系数C1～C8的矩阵形式：

d=K1C，f=K2C

(16)

式中：C=[C1C2C3C4C5C6C7C8]T为常数矩阵，K1和K2为与ω相关的系数矩阵。

由式可直接表示出力向量和位移向量的关系：

f=KDd

(17)

式中：KD=K2K1-1，即为动刚度矩阵。

由前文的推导过程可见，动刚度法的精度与划分单元数量无关，因此对于沿轴向几何形状及材料不发生改变的情况下，任意长度的管道都仅需要用一个单元模拟，且对于计算频域没有特别限制。

3 算例分析与讨论

由数据对比可见，本文的计算结果与文献基本一致。不过本文计算的横向模态数值略低，因为本文的理论中考虑了梁的剪切变形，而文献中采用的是Euler梁模型。虽然本例计算的已为细长梁，但随着模态阶数升高和流速增大，误差仍会略有增加。注意到在流体模态和轴向模态中，文献结果的实数部分变化不明显，而本文的计算结果中考虑到了摩擦因数随流速的变化，随流速增大，固有频率实数部分减小，虚数部分增大。

表1 不同流速下均质输流管道振动固有频率Tab.1 Natural frequencies(Hz)for the vibration of homogenous pipes conveying fluid with different velocities Hz

(2)本例计算两端简支的功能梯度充液直管，长度为L=6 m，截面内径为0.2 m，外径为0.4 m，管壁由铝-SiC陶瓷材料复合而成，内壁材料为SiC陶瓷，杨氏模量E1=427 GPa，泊松比μ1=0.17，密度ρ1=3 100 kg/m3，外壁材料为铝，杨氏模量E2=70 GPa，泊松比μ2=0.33，密度ρ2=2 700 kg/m3，在本例中用二十层均匀离散单元。

图4 在两端简支直管道上施加单位横向载荷Fig.4 The unit transverse load applied on the simply supported straight pipe.

如图4所示，在管道的L/12处施加单位横向载荷，前文建立的方程中，轴向与横向、流体均是耦合的，因此在结构上只施加了横向载荷即可同时引起轴向及流体响应。图5绘制了当梯度指数为n=0时点L/12处在频域0～550 Hz的速度响应，响应曲线的峰值处的频率对应了固有频率。轴向及流体响应是由耦合项引起的，因此其振动的幅值小于横向单位力引起的横向振动。由图5可见，流体响应曲线包含了所有模态，而轴向和流体响应曲线上比横向响应曲线多出的波峰对应了轴向模态(A)及流体模态(F)，以此响应曲线即可区分结构模态和流体模态。

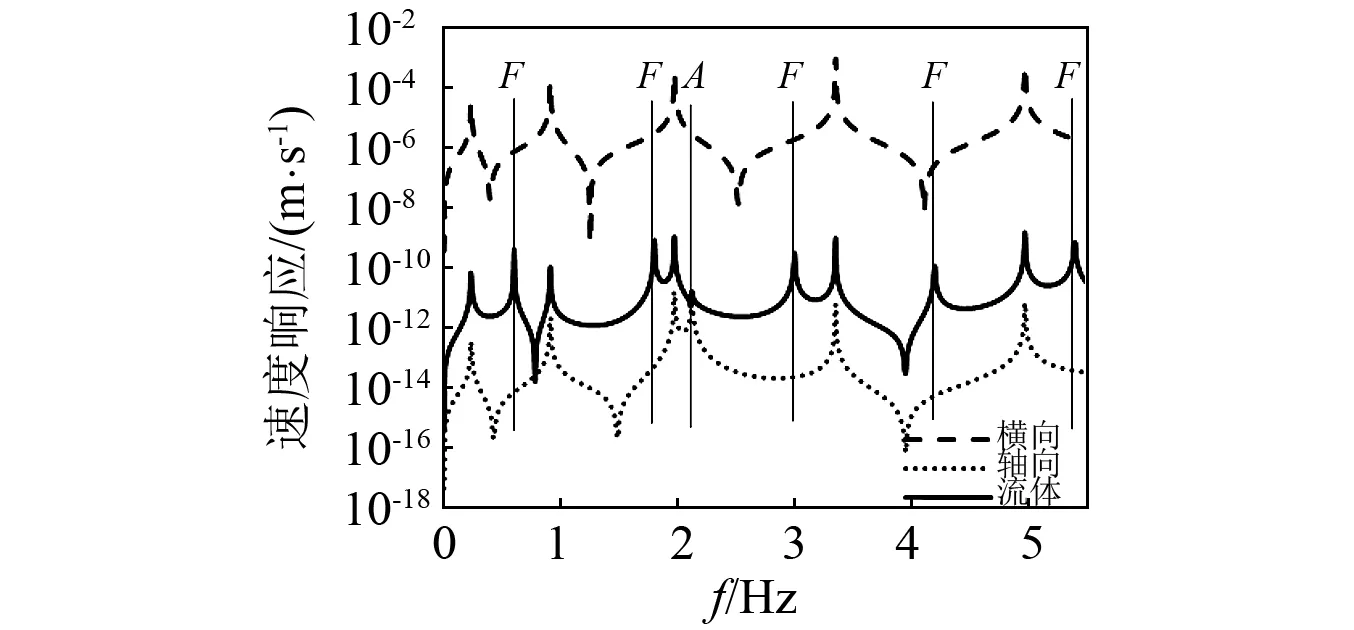
图5 n=0，点L/12处0-550Hz频域内速度响应曲线Fig.5 n=0,velocity responses at the point L/12 in frequency domain 0～550 Hz

图6 不同梯度指数下速度响应曲线Fig.6 Velocity responses with different gradient indexes.

图6中分别为在不同梯度指数下横向、轴向及流体的速度响应曲线。由图线可见，随n值的增大，结构速度响应曲线均向右移动，即横向和轴向固有频率均明显提高，且随着阶数的升高，改变幅度也变大。而值得注意的是在流速响应曲线中，显然有一些波峰的位置改变幅度很小，几乎重合，这些峰值对应的是流体模态，在图中以F表示。由此可见，管道材料的变化对于管道结构本身的影响较大，而对于其内部的流体影响很小。

(3)工程中常见的薄壁管道，流速增大情况下固有频率降低，如算例1所示。当第一阶固有频率降低至零时，则管道发生失稳。而由算例2可见，将功能梯度材料应用于管道结构上，能显著提升固有频率，因此能有效地延缓因流速导致的管道失稳的发生。图7展示了将算例2中的功能梯度材料应用于算例1的薄壁管道中，在流速增大时第一阶固有频率的变化情况。由图7曲线对比可见，随n值的增大，失稳临界流速显著提高，保证了管道在较低流速下的稳定性。

图7 不同梯度指数下第一阶固有频率随流速变化曲线Fig.7 Curves of the first natural frequency with the increase of flowing velocities under different gradient indexes.

当管内流速为10 m/s时，在管道一端1/10处施加简谐激励力sin(2πt)，对该点的频域响应进行傅里叶逆变换可得到时域响应，管道材料取不同n值时在0～1 s内的横向位移响应曲线如图8所示。随着n值的增大，管道的振动幅度也有了显著的降低。此外值得注意的是，n值由0增加至0.5，位移降低得非常显著，而随着n值的进一步增大，尤其在n值增加到2以上，位移的变化幅度逐渐变小。从功能梯度的结构来分析，图9展示了取不同梯度指数时沿半径方向变化的杨氏模量变化曲线，其他材料参数也有类似的变化规律。当n增大时，杨氏模量呈增大趋势，从而管道的有效刚度也增大，因此位移振幅减小。管壁的平均杨氏模量值显然是与曲线下覆盖的面积呈正比的，当梯度值从0增加至0.5时，杨氏模量的增长量大，而随着n值的进一步提升，曲线的斜率逐渐降低，材料参数的增长逐渐缓慢。

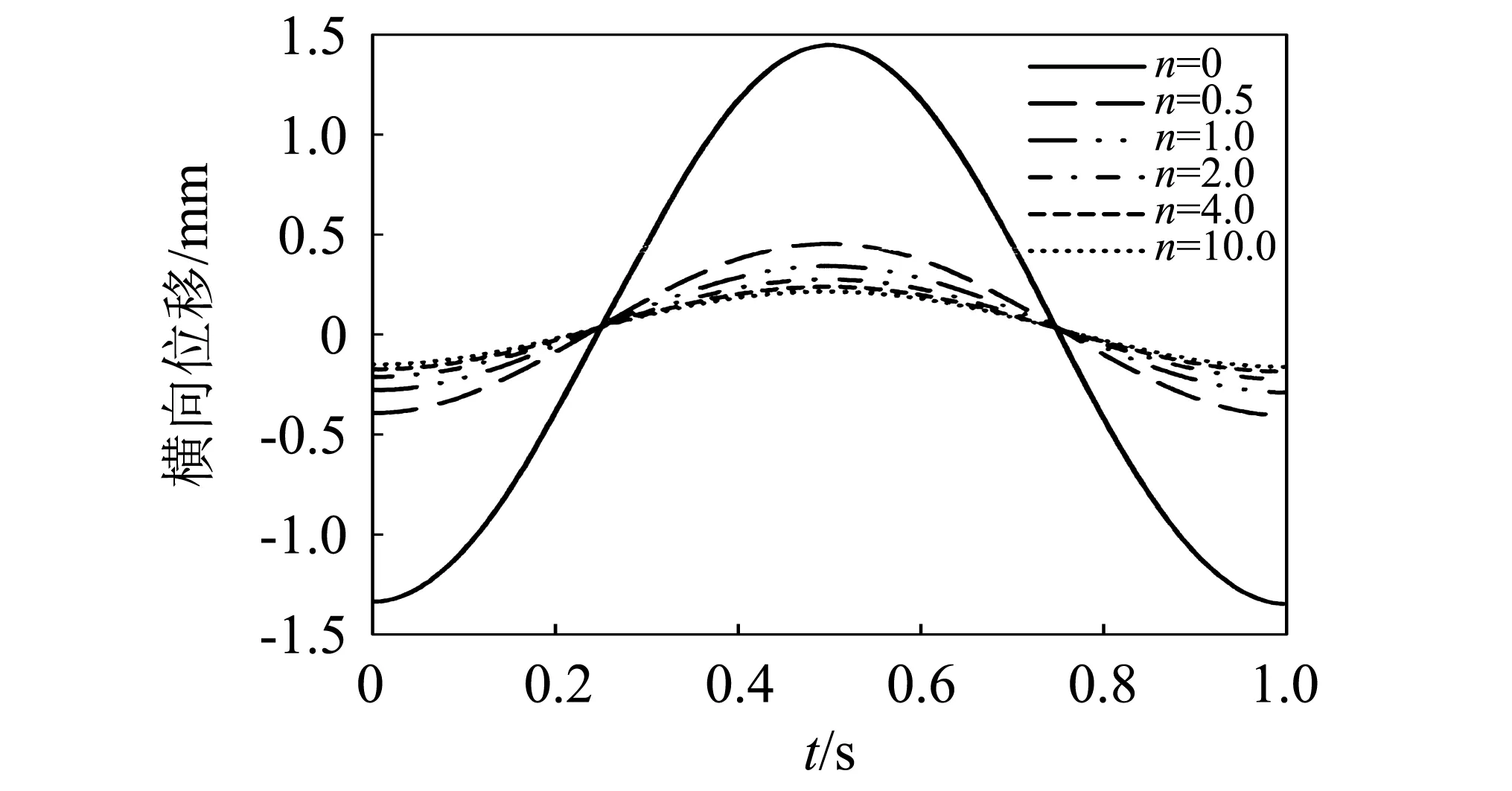
图8 不同梯度指数横向位移时域响应曲线Fig.8 Transverse displacement responses in time domain with different gradient indexes.

从提高管道的稳定性和降低振动幅度的角度来说，这种功能梯度材料输流管道的梯度指数n越大越好，但是显然实际应用还要考虑到材料的成本、制作工艺等因素，此外以这种陶瓷-铝功能梯度材料为例，n值越大，陶瓷的体积率就越高，而虽然陶瓷材料的刚度更大，但其耐冲击性能低，极易发生脆性断裂。以本文的材料参数变化规律来说，当n>2时，其对于管道动态特性的影响并不大，因此对于本例的功能梯度输流管道的梯度指数取为2是比较合适的。未来在工程中若要在管道上应用功能梯度材料，在选取梯度指数时应综合考虑其对结构的影响、材料参数的变化规律以及成本和材料优缺点等实际因素。

图9 不同梯度指数的杨氏模量变化曲线Fig.9 Curves of Young’s modulus with different gradient indexes.

4 结 论

本文应用离散化的思想，将功能梯度材料沿厚度方向划分为若干均匀层，考虑流体与管壁间的相互作用，建立了功能梯度输流管道的耦合振动模型，并应用动刚度法求解了管道振动的固有频率及频域、时域响应。当材料退化为普通均质材料时，计算结果与文献结果完全一致，说明了本文所建立公式及计算方法的正确性。此外功能梯度管道的算例反映了功能梯度材料梯度指数的变化在提高结构固有频率、延缓管道失稳方面的积极意义。本文的理论对于功能梯度材料和层合复合材料具有普适性，为新型复合材料在管道上的应用提供了理论依据。