考虑径向间隙的非理想双圆弧滚道滚珠丝杠副接触角建模和分析

2019-10-30姜洪奎宋现春许向荣李彦凤王乐源荣伯松

振动与冲击 2019年20期

姜洪奎，宋现春，许向荣，李彦凤，王乐源，刘涛，杜伟，荣伯松

(1.山东建筑大学机电工程学院，济南 250010；2.山东济宁博特有限公司，济宁 272071)

精密滚珠丝杠副是数控机床进给系统的关键部件，由于滚珠丝杠副传动效率高，且能够消除传动间隙、精度高以及运动平稳，因而在数控机床和机械制造中得到广泛应用。双圆弧滚道(哥特式滚道)是目前精密滚珠丝杠副广泛采用的截型形式。相对于单圆弧滚道，双圆弧滚道型面的滚珠丝杠副能够使接触角基本保持不变，从而其传动效率、承载能力和轴向刚度比较稳定，但是双圆弧滚道的精磨削相对于单圆弧滚道磨削比较困难，在这一磨削工艺过程中即使采用砂轮修整方法，也容易造成滚道的截形误差[1]。在实际生产中，螺母侧和丝杠侧滚道加工后的接触角与理想接触角相差较大，有的滚道相差2°～3°，哥特式滚道实际加工误差如图1所示。弹性变形接触角是衡量滚珠丝杠副装配质量的关键技术参数。弹性变形接触角的大小不仅决定了滚珠丝杠副的整体传动效率，而且与载荷分布、刚度、摩擦力矩、磨损等性能密切相关[2-5]。

由于精密滚珠丝杠副的弹性变形接触角无法直接测量，应用成熟的力学模型对弹性变形接触角进行理论计算成为控制滚珠丝杠副装配质量的主要方法。由于滚动轴承与滚珠丝杠副存在结构的相似点，而且其弹性接触角[6-8]的计算相对成熟，因此许多工程人员往往参考其计算模型进行计算。胡建忠等[9]以双螺母定位预紧滚珠丝杠副为研究对象，对轴向接触刚度的影响因素进行分析。Wang等[10]在计算滚珠丝杠副弹性接触角的理论指导下，探索了使用磁致伸缩材料改变滚珠丝杠副预紧力的方法。赵国平等[11]根据弹塑性变形理论，研究了在超负荷工况下的滚珠丝杠副变形和刚度的计算方法。赵训贵等[12]在假设弹性变形接触角等于45゜的条件下，研究了制造误差对弹性变形接触角的影响，并给出了计算弹性接触角的简易公式。李梦奇等[13]基于赫兹理论和滚道控制理论，建立了滚珠丝杠动态接触角模型，得到面向结构参数的接触角非线性方程组。对于研究不同工况下的结构参数对滚珠丝杠副动态接触角的影响规律有很好的指导作用。张承瑞等[14]基于MEAS仿真建模方法，建立了考虑黏性摩擦和传动刚度的滚珠丝杠进给系统的二阶数学模型，对于提高滚珠丝杠进给系统的控制性能具有重要的工程应用意义。黄俊等[15]考虑丝杠螺母副,支撑轴承及直线滚动导轨结合面参数对动态刚度的影响，利用能量法建立了双驱动进给系统多自由度模型为了研究双驱动进给系统的动态特性。杨勇等[16]充分考虑滚珠丝杠进给系统的结构柔性以及耦合特性,构建了滚珠丝杠进给系统多柔体动力学模型,为实现滚珠丝杠进给系统与伺服控制系统的集成建模提供了重要理论和方法。

这些计算方法和理论或者没有考虑径向间隙、滚道参数不相等的情况或者限定了弹性变形接触角的取值，不能适用于新型的具有不同滚道参数的滚珠丝杠副的装配和研制开发。

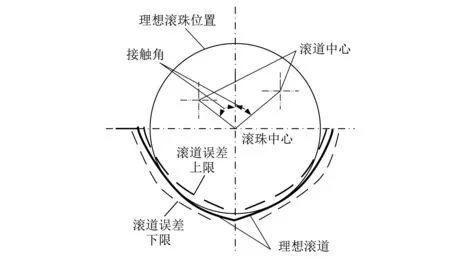
图1 螺纹滚道实际加工廓形Fig.1 The actual machining profiles of Gothic raceway

基于上述原因，本文充分考虑滚珠丝杠副在实际加工中产生的滚道截型磨削误差、加工接触角不对等、径向间隙等因素，以非理想滚道的滚珠丝杠副为研究对象，根据赫兹理论和几何变形关系建立了通用的滚珠丝杠副弹性接触角的计算模型和相应的数值方法，分析了螺母滚道、丝杠滚道、滚珠半径、径向间隙的几何误差对弹性变形接触角的影响。该研究对研制开发新型滚珠丝杠副产品、优化滚珠丝杠副装配工艺、提升滚珠丝杠副的保养效率具有实际意义。

1 非理想滚道弹性变形接触角建模

为了使问题得到简化，准确地构造求解模型，本文做出以下假设：①滚珠丝杆副中各滚珠受力均匀；②假设滚珠不出现打滑现象；③滚珠与滚道之间为赫兹接触；④非理想滚道为几何中心与滚珠中心成一定角度的双半圆弧。

1.1 非理想滚道的初始接触角

图2 消除径向间隙前后滚珠与滚道几何关系Fig.2 Geometric relation between ball and raceway before and after diametric clearance is diminished

螺母没有发生平动前，滚珠中心位于点Oon(0,Sd/2)处时，直线OonOn与y轴之间夹角为螺母侧设计接触角αn，点On(xn,yn)位于螺母侧右半外圆曲率中心，设rs,rn,rb,分别为丝杠侧滚道半径、螺母侧滚道半径、滚珠半径，因此，

(1)

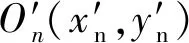
(2)

滚珠中心位于点Os(xs,ys)处时，滚珠与丝杠侧滚道右半外圆接触，直线OosOs与y轴之间夹角为丝杠侧设计接触角αs，因为OosOs的距离为滚道半径与滚珠半径之差rs-rb，所以

(3)

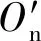
(4)

(xo-xs)2+(yo-ys)2=(rs-rb)2

(5)

(6)

(7)

将公式(2)，(3)代入式(7)，可以得出初始接触角α0为

(8)

1.2 滚珠与滚道之间的弹性变形协调模型

(rn+rs-2rb)cosα0=(rs+rn-2rb+δns+δnm)cosα

(9)

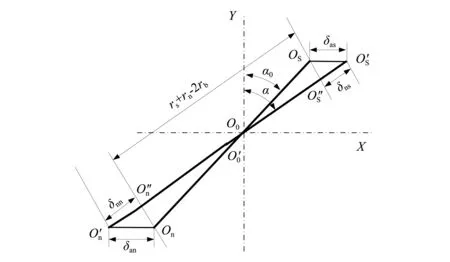
图3 预载后滚珠与滚道之间的弹性变形协调几何关系Fig.3 Displacements of ball and raceway before and after axial preload is applied

将式(8)代入式(9)可得弹性变形接触角α为

(10)

由式(10)可以看出，只要求出滚珠与两侧滚道的法向变形量就可以得出弹性变形接触角α。

由于轴承钢是滚珠丝杠副常用的材料，根据赫兹理论[14]可得出，滚珠与滚道之间的法向变形量δns和δnn为

(11)

式中i=n表示螺母侧，i=s表示丝杠侧，Qi为单个滚珠承受的法向载荷，∑ρi为滚珠与滚道接触表面的曲率和。根据文献[17]单个滚珠承受的法向载荷Qi的计算公式为

(12)

式中：Fa为丝杠副所承受的轴向预紧载荷，z为单个螺母内的承载滚珠个数，λ为螺旋升角。忽略重力对滚珠平衡状态的影响，滚珠在两侧滚道内法向载荷大小相等，即Qn=Qs。将式(11)～(12)代入式(10)可得初始接触角α0和实际弹性接触角α之间的关系式。

(13)

式(13)涉及到椭圆积分是一个非线性程度较高的方程，需要采用相应的数值算法对其进行求解。该方法已获得专利[18]。

2 案例及讨论

为了验证本文提出的计算方法的通用性和正确性，应用本文提出的计算方法对双半内圈球轴承和3210的滚珠丝杠副进行了计算和对比分析。

2.1 双半内圈球轴承

双半内圈球轴承是非等适应度圆弧滚道的另一个特例。如图4所示双半内圈球轴承的滚珠和滚道之间的几何关系。双半内圈球轴承的外圈为单圆弧，双半内圈球轴承的内圈为两个半圆弧组成。在内圈磨削时，在两半内圈之间加有垫片，当移去垫片并将双半内圈靠紧组合成轴承内圈。垫片角αs(即滚珠与外滚道的接触角)通过垫片厚度确定。由于螺母滚道为单圆弧，可以确定滚珠与螺母侧接触角为αn=0，代入式(8)可以得出双半内圈球轴承的初始接触角α0为

(14)

公式(14)与文献[14]中的计算公式相同。

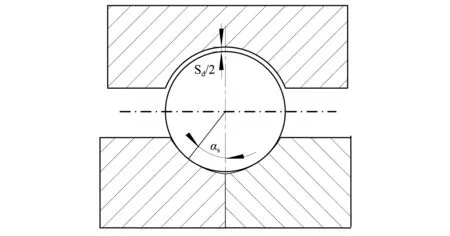
图4 双半内圈球轴承垫片角Fig.4 the diametric clearance of split inner-ring ball bearing

2.2 方法对比

以双圆弧型的滚珠丝杠副为例，其主要结构参数为：钢球5.953 mm，公称直径32 mm，径向间隙0.038 mm,滚珠与滚道的弹性变形法向变形量0.069 mm。应用本文所提出计算方法和文献[12]中关于弹性接触角的计算方法进行对比。

表1 新方法与文献[8]方法计算结果对比Tab.1 Comparison of results from new method and method from literature [8]

从表1给出的两种计算方法的计算结果可以看出：文献[8]计算方法只能对丝杠、螺母滚道适应比、接触角均相同的情况进行计算，当丝杠、螺母滚道的适应比、接触角不完全相同时就无法给出相应的结果；在滚道适应比、接触角相同的情况下，两种方法的计算结果基本一致；文献[12]的计算方法没有考虑导程的因素，如在滚道几何参数不变的情况下，导程10 mm和20 mm所得出的结果没有变化。

新方法与文献[12]的计算结果存在差异的原因是由于二者的方法不同。文献[12]的关于双圆弧滚道的弹性接触角的计算方法求解思路是先假定弹性接触角等于45°，然后对弹性变形接触角的几何关系式进行微分，得出设计接触角增量、滚道尺寸增量、滚珠半径增量和弹性接触角之间的关系。由于采用微分方法得出各个几何因素之间的关系式，因此各个参数的变动量必须变化较小，才能符合方法二的要求。本文的模型考虑了滚珠丝杠副公称直径和螺旋升角因素，用数值求解方法求解变形协调方程，避免了计算过程中偏差值较大的情况，而且没有等接触角、等滚道半径的限制。因此与原有手段相比，本文提出的计算方法准确度高，通用性强，应用广泛，所得结果更可信。

3 非理想滚道截形误差的影响分析

以双圆弧滚道3210滚珠丝杠副为研究对象，分析设计接触角误差、滚道半径误差对弹性变形接触角的影响。3210型滚珠丝杠副的主要结构参数如表2，滚珠和丝杠、螺母的材料都是轴承钢。

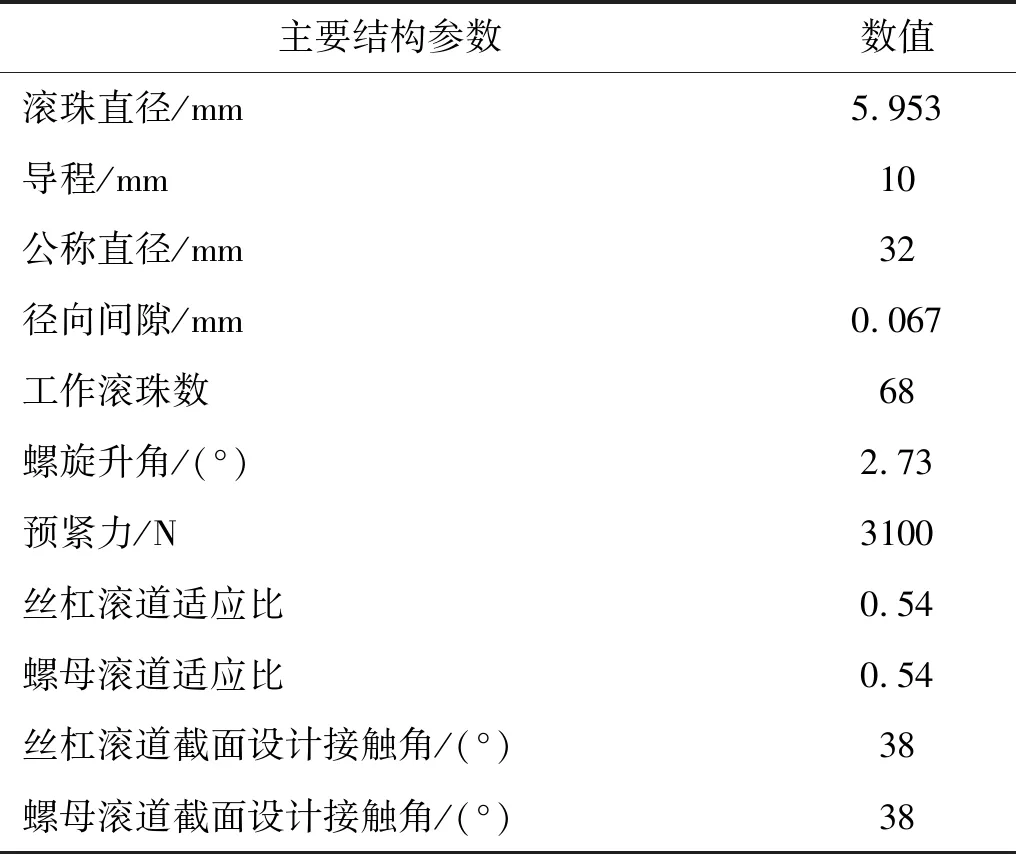
表2 滚珠丝杠副参数表Tab.2 Parameters of example ball screw mechanism

(1)不对等的螺母、丝杠滚道设计接触角的影响

为了方便分析螺母、丝杠滚道接触角的不对等对弹性变形接触角的影响，本文以3210滚珠丝杠副为研究对象，分别设定螺母、丝杠滚道设计接触角变化范围36.5°～39.5°，滚道适应比为0.54，以滚珠与滚道的法向弹性变形量0.006 9 mm为加载条件，径向间隙0.067 mm，应用本文方法计算相同滚道半径情况下不同滚道设计接触角对滚珠丝杠副的弹性变形接触角变化情况，其计算结果如图5。

图5 不同设计接触角条件下的弹性接触角等值线图Fig.5 The contour map of elastic contact Angle under different design contact angle

从图5可以看出，不同设计接触角条件下滚珠丝杠副弹性接触角等高线沿着图8的对角线对称分布。滚珠丝杠副弹性接触角等于45°的等高线近似一个斜放置的“M”字分布。在丝杠侧设计接触角(37.2°～38.8°)、螺母侧设计接触角(37.2°～38.8°)的范围内，45°的等高线的形状接近直线，周围的等高线分布范围最为稀疏，而在图5的四个角处等高线分布相对致密，丝杠侧、螺母侧设计接触角分别等于(37.8°，37.8°)是“M”线的核心位置。因此从设计角度来看，37.8°是丝杠侧、螺母侧滚道设计接触角的最佳值，因为这样可以使得两侧滚道的接触角加工误差对滚珠丝杠副的弹性接触角影响最小。从滚珠丝杠副的装配理论来看，由于45°等高线接近斜度45°的直线，因此只要丝杠侧、螺母侧实际的接触角满足之和等于75.6°就可以保证滚珠丝杠副弹性接触角等于45°的最优装配性能。

(2)不对等的螺母、丝杠滚道半径的影响

螺母、丝杠滚道半径不标准、不对等是丝杠副磨削过程常见的加工误差之一。以3210滚珠丝杠副为研究对象，分别设定螺母、丝杠滚道适应比变化范围0.525～0.555，同样以滚珠与滚道的法向弹性变形量0.006 9 mm为加载条件，丝杠侧、螺母侧接触角均等于38°，径向间隙0.067 mm，应用本文方法计算相同滚道设计接触角下不同滚道半径情况对滚珠丝杠副的弹性变形接触角变化情况，其计算结果如图6。

从图6可以看出，不同滚道适应比条件下滚珠丝杠副弹性接触角等高线沿对角线对称分布。滚珠丝杠副弹性接触角等于45°的区域分布在一个长轴与对角线平行的近似椭圆以及两个近似半圆区域内。在预紧载荷、径向间隙不变的情况下，在螺母滚道适应比：0.531～0.548，丝杠滚道适应比：0.548～0.531这个近似椭圆区域内，滚珠丝杠副弹性变形接触角的变化基本在45°附近。即在一定几何参数范围内滚道误差的变化对滚珠丝杠副弹性变形接触角的影响相对设计接触角的影响较小。

图6 不同滚道适应比条件下的弹性接触角等值线图Fig.6 The contour map of elastic contact Angle under different ratio of raceway

(3)径向间隙的影响

不同加工方式的滚珠丝杠副的径向间隙也各不相同，如对于公称直径28～32 mm之间的扎制丝杠最大间隙在0.14 mm，而同样直径范围内的精密滚珠丝杠副则在0～0.005 mm。为了方便分析径向间隙对弹性变形接触角的影响，本文以3210滚珠丝杠副为研究对象，分别设置径向间隙为0.001 mm，0.01 mm，0.04 mm，螺母、丝杠滚道适应比等于0.54，以滚珠与滚道的法向弹性变形量0.006 9 mm为预紧条件。针对不同的径向间隙，绘制相应的滚珠丝杠副的弹性接触角等高线，如图7所示。

图7 不同径向间隙下的弹性接触角等值线图Fig.7 The contour map of elastic contact Angle under different radial clearance

由图7可以看出：图(b)中45°的弹性接触角等高线位于图的中心，而且呈现为“M”形状；图(a)，(c)中的45°的弹性接触角等高线位于图的斜上角，而且呈现为“V”形状；图(a),(b),(c)中最为稀疏的等高线中心都各不相同。当径向间隙为0.01 mm时，45°的弹性接触角等高区域最大，因此三种径向间隙的对比中，0.01 mm是3210型滚珠丝杠副在预紧变形为0.006 9 mm条件下的最佳值。图7比较结果可以得出，滚珠丝杠副径向间隙是影响滚珠丝杠副弹性接触角的区域形状大小的主要因素，因此要根据具体的滚珠丝杠副滚道的加工方式和加工误差，合理设计径向间隙的大小。

(4)滚珠大小的影响

在实际滚珠丝杠副的装配中，往往采用非标滚珠调节滚珠丝杠副的弹性接触角，所以分析滚珠直径大小对弹性接触角的影响非常有必要。以3210滚珠丝杠副为研究对象，螺母、丝杠滚道适应比变化范围0.54，径向间隙0.047 mm，以滚珠与滚道的法向弹性变形量0.006 9 mm为加载条件，参考轴承钢球国家标准分别设定滚珠直径大小为5.953 mm， 5.954 mm，5.958 mm。应用本文方法计算不同滚珠直径对滚珠丝杠副的弹性变形接触角等高线变化情况，其计算结果如图8。