海马真空冷冻干燥特性及其动力学模型
2019-10-30吴靖娜陈晓婷刘智禹廖登远黄鹭强陈由强
吴靖娜,陈晓婷,刘智禹*,廖登远,黄鹭强,陈由强
〔1.福建省水产研究所,福建 厦门 361013;2.国家海水鱼类加工技术研发分中心(厦门),福建 厦门 361013;3.海洋生物医药与制品产业化开发技术公共服务平台,福建 福州 350117〕
海马始载于《本草经集注》,是硬骨鱼纲(Osteichthyes)、海龙目(Syngnathiformes)、海龙科(Syngnathidae)、海马属(Hippocampus)动物的统称,分布于东海和南海等区域,主产于福建、广东、台湾和海南。海马为我国名贵中药材,《中国药典》记载:“海马味甘、咸,性温,归肝、肾经;具有温肾壮阳,散结消肿的功效,主要用于阳痿、遗尿、肾虚作喘、癥瘕积聚、跌扑损伤;外用痈肿疔疮”[1]。现代药理研究表明,海马不仅具有激素样作用,增强造血功能,还显示了抗肿瘤、抗疲劳、抗衰老、增强学习记忆力和Ca2+阻断等作用[2]。目前关于海马的研究,大多数集中于海马品种鉴定[3]、养殖应用[4]、质量研究[5-6]和粗提物的药理活性研究,而关于海马干燥的研究尚不充分,相关文献不多。
新鲜海马水分含量高,不易储藏,易发生腐败变质,脱水是延长其保质期的方法之一。海马干燥在我国有一定的历史,主要以日晒风干与热风干燥为主。然而,日晒风干主要依靠自然条件控制,产品易受环境影响,产品质量参差不齐,热风干燥由于能耗高、温度高,容易造成产品热损伤和过度氧化等问题[7],选择合适的干燥方法已成为海马干燥加工的客观要求。近年来,真空冷冻干燥[7]、冷风干燥[8]和微波干燥[9]等干燥方式被广泛应用于水产品的干燥技术中,其中,真空冷冻干燥是将物料冷冻至共晶点温度以下,并在真空条件下获得疏松多孔、复水快的干燥产品[10],极大地保留了产品的营养物质和形态,已被广泛应用于牡蛎[11]和对虾[7]等水产品的干制中。
数学干燥模型可通过建立干燥过程中各参数之间的定量关系和规律,比较准确地描述和预测产品干燥过程。近年来,国内外对农产品干燥模型研究已有大量的研究报道,各种数学模型如Lewis函数、Page函数、Henderson and Pabis函数及Logarithmic函数等被广泛应用于描述干燥过程[12]。因此,本研究采用真空冷冻干燥对海马进行干燥,对其干燥特性和有效水分扩散系数进行研究,并使用8种常见的干燥数学模型对其干燥过程进行拟合,建立干燥数学模型,以期为真空冷冻干燥技术在海马干燥的应用提供技术支持和理论依据。
1 材料与方法
1.1 材料与仪器
海马,捕捞于福建省漳州市东山县,体重为(5.50±0.43)g。
SCIENTZ-10N真空冷冻干燥机(宁波新芝生物科技股份有限公司)。
1.2 试验方法
真空冷冻干燥条件:将海马置于-18℃冰箱中预冻过夜,然后在干燥温度30℃、真空度为300 Pa的条件下干燥,测定海马的初始质量,每隔2.5 h测定样品的质量,待最终产品达恒重,停止干燥,每组做9个平行。
1.3 测定指标及方法
1.3.1 含水率测定
采用GB 5009.3—2016《食品安全国家标准 食品中水分的测定》。
1.3.2 干基含水率
按公式(1)计算[13]:
(1)
式中:Mt为物料干基含水率,%;mt为t时刻物料的质量,g;md为绝干物料的质量,g。
1.3.3 水分比(Moisture ratio,MR)
按公式(2)计算[8]。
(2)
式中:MR为水分比;Mt为物料t时刻干基含水率,%,M0为物料初始干基含水率,%。
1.3.4 水分有效扩散系数(Effective diffusivity coefficient,Deff)
作lnMR与干燥时间t的关系图,并进行线性拟合,求直线的斜率k,代入公式(3)中可求出水分有效扩散系数。
(3)
式中:Deff为水分有效扩散系数,m2/h;t为干燥时间,h;L为样品厚度,m。
1.3.5 干燥动力学数学模型的选择与建立
采用表1中8种常见的干燥模型对海马干燥曲线进行拟合,并通过决定系数(Correlation coefficient,R2)、卡方检验值(Reduced chi-square,χ2)和均方根误差(Root mean square error,RMSE)来评价模型的拟合度,从中筛选出合适的干燥动力学模型。

表1 8种干燥模型及其参数
1.4 数据处理与分析
采用Origin 8.5进行线性回归拟合和非线性回归拟合。
2 结果与分析
2.1 干燥动力学分析
由图1可知,水分比随脱水时间的延长呈指数下降趋势,前期下降较快,后期逐渐趋于平缓,该结果与多数物料的干燥特性相似[14];干燥7.5 h能除去海马80 %的水分,表明干燥初期,干燥从冻层表面开始,海马传热和传质阻力较低,干燥速率提升非常迅速,极快干燥了湿物料[15],干燥25 h后海马达到干燥终点。
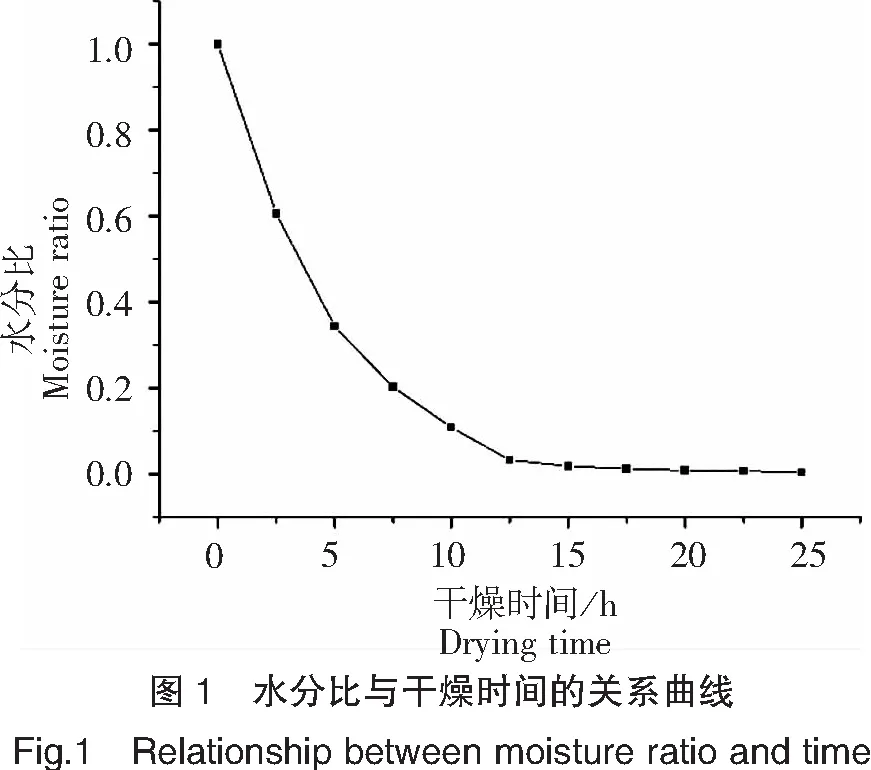
2.2 水分有效扩散系数的分析
物料的干燥是一个复杂的传热与传质同时发生的过程。干燥空气与湿物料间存在的温度梯度和湿度梯度,是物料水分扩散并实现干燥的主要动力。物料中水分扩散分为水分外扩散阶段和水分内扩散阶段[16]。为了简化计算结果,采用液态扩散理论来描述食品物料的干燥过程,该理论不考虑干燥过程中的扩散推动力,采用有效水分扩散系数Deff来表征干燥过程中水分迁移的平均速度[16]。真空冷冻干燥海马的lnMR与干燥时间t之间的线性拟合关系见图2。经拟合,获得海马lnMR与t线性拟合方程为lnMR=-0.240 8t+0.047 7,线性拟合决定系数R2为0.989 5,表现出较好的拟合度。通过公式(3)计算出海马真空冷冻干燥的Deff为2.442 3×10-10m2/s,符合食品物料干燥有效水分扩散系数Deff10-10m2/s~10-8m2/s数量级范围[17]。
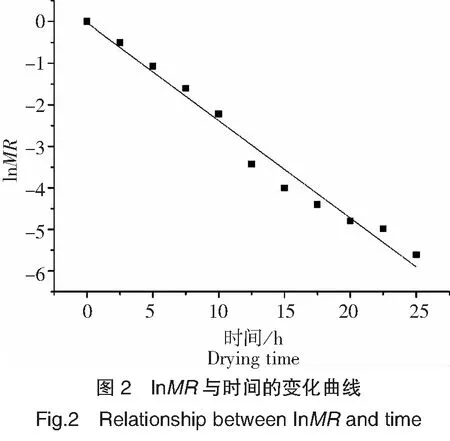
2.3 干燥模型的研究
干燥动力学是干燥过程中物料的水分比MR与干燥时间t的函数关系式,间接反应了干燥过程中物料的传热和传质特性。为了更好地描述海马真空冷冻干燥的变化规律,参考8种干燥模型(表1)对干燥曲线进行非线性拟合,根据决定系数R2、卡方检验值χ2和均方根误差RMSE判别模型的拟合程度,R2越接近1,χ2和RMSE越小,说明干燥曲线拟合相关性较好,海马真空冷冻干燥曲线的拟合结果见表2。
由表2可知,几种模型中Lewis、Page、Henderson and Pabis和Logarithmic的R2均在0.99以上,其χ2在5.961 9×10-5~2.644 5×10-4范围内变化,RMSE在2.090 0×10-4~6.725 0×10-3范围内变化,4个模型的拟合效果高于其他模型,说明能够采用Lewis、Page、Henderson and Pabis和Logarithmic模型来描述海马真空冷冻干燥过程中物料水分比的变化情况。其中,Page模型的R2最高,χ2和RMSE最低,说明Page模型具有更优越的拟合效果,所以本研究选用其作为描述海马真空冷冻干燥的最适数学模型。目前被广泛应用于农产品的干燥模型主要有理论模型、半理论模型、半经验模型和经验模型4种[12],本研究所选用的Page函数是建立在牛顿冷却定律的基础上,由Lewis函数修订而来,式中k和n为与干燥介质有关的经验常数,该模型被广泛用于描述水产品和果蔬产品的干燥规律[12,18]。
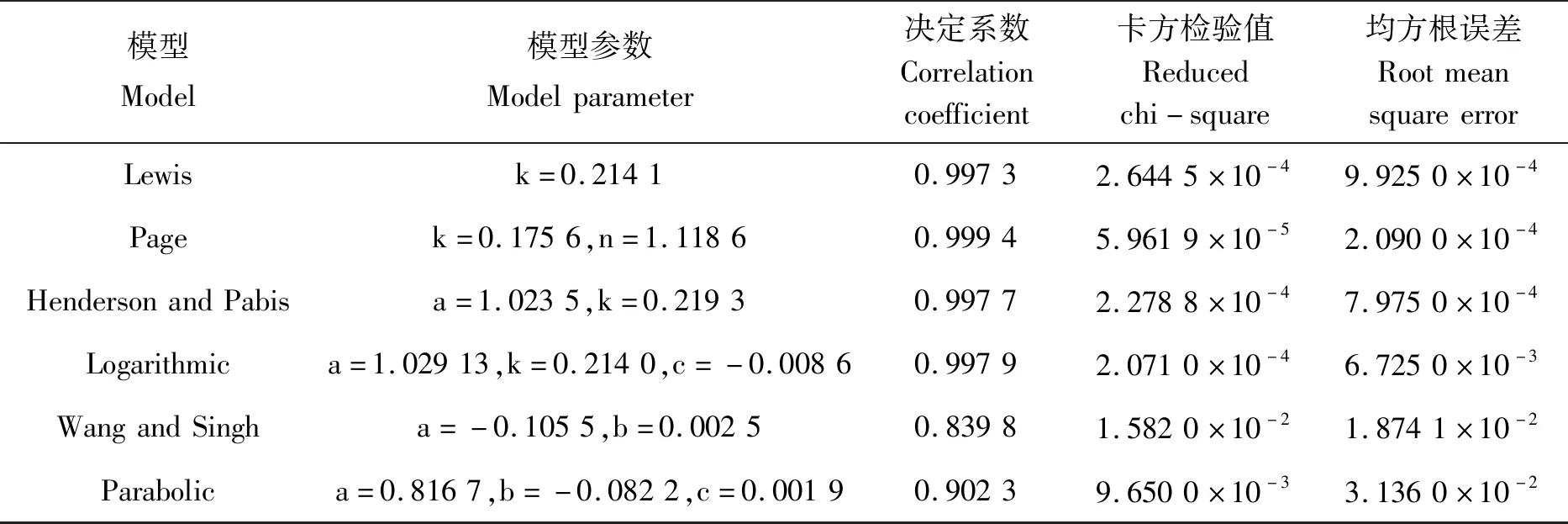
表2 数学模型拟合结果
3 结论
本研究采用真空冷冻干燥对海马进行干燥,对其干燥特性及干燥模型进行研究。干燥25 h后海马达到干燥终点,其干燥过程的有效水分扩散系数为2.4423×10-10m2/s。为了对海马干燥过程中的水分散失情况进行描述与预测,使用8种常用的干燥数学模型对真空冷冻干燥的干燥过程进行拟合,并从中筛选出最适合的干燥动力学模型,确定模型参数,结果显示Page模型可以很好地描述海马真空冷冻干燥过程。
