基于鱼群算法的船舶避浅航线设计
2019-10-30赵延鹏张超越
陈 晓, 戴 冉, 赵延鹏, 张超越
(大连海事大学 航海学院, 辽宁 大连 116026)
船舶搁浅事故是船舶在海上的常发事故之一,现阶段对于船舶避浅大部分的研究处于搁浅事故概率的计算,主要采用的分析方式是基于事故树模型[1],并在此基础上引入模糊原理[2]、贝叶斯网络[3]等方法不断地修正搁浅概率模型,以及采用设置警戒区域的方式对可能会搁浅的船舶进行报警处理[4]。上述方法多处于理论研究阶段,虽然能够分析发生搁浅事故概率,但是对于如何避浅的研究还不够深入。船舶交通服务(Vessel Traffic Services,VTS)[5]作为海上交通安全保障的重要机构,主要的职责是保障船舶航行安全,根据其完善的法律法规和相关航行管理规范,基于丰富的交通情况数据和环境数据,能够做出正确、有效的决策判断。[6]目前,VTS值班员主要是根据自身的经验判断,指导危险水域的船舶航行,这种方式不但增加值班员的工作量,而且对值班员自身的素质有较强的依赖性。因此,研究智能算法,规划船舶避浅航线,为值班员的决策提供理论依据是具有一定现实意义的。
为实现相关危险区域和水深点信息的呈现,利用栅格法,对船舶航行区域进行格栅处理,并在此基础上,以转向角度和转向点数量作为约束条件,对可能发生搁浅的船舶规划新的航线,从而达到船舶避浅的目的。
1 海图模型建立
对于船舶航行的浅滩水域,不能直接使用其中危险区域的信息,需要对相关信息建立模型。利用格栅化的方法,提取浅滩区域的信息,在生成的格栅图中规划船舶的避浅航线。
1.1 栅格法
栅格法[7]是20世纪60年代提出的一种对地图的处理方法,栅格法将地图环境分解为一系列具有二值信息的网络单元格,环境中的障碍区域在整个规划的过程中位置和大小不发生改变。利用尺寸相同的栅格对二维的环境空间进行划分,栅格的大小自定,对于不含任何障碍物的栅格称为自由栅格,反之称为障碍栅格。[8]
1.2 栅格海图构建
首先对所选海图内的浅滩区域进行扩展,设置安全距离h。h的设置原则:
1) 安全区域外的水深满足船舶的吃水要求。
2) 根据船舶的操作性能,船舶在做转向操作时,船体不会触及安全距离的边界。把已扩展的区域定义为安全区域,见图1。在航线的重新规划中,即使靠近已扩展的浅滩区域,也能保障重新规划后的航线符合安全操作的要求。
基于浅滩区域扩展后的海图,假设所截取的海图环境为E,对于不满一个栅格的不可航行区域算一个栅格,建立数学模型为
E={gij|gij=0或1,i∈L/b,j∈W/b}
(1)
式(1)中:L为截取海图的最大长度;W为截取海图的最大宽度;b为栅格的长宽尺度;gij=0为可航行区域;gij=1为浅滩或危险区域。利用MATLAB软件对截取海图上的区域进行仿真,得到格栅化海图示意见图2。图2中:黑色区域为障碍栅格,即不可航行的浅滩区域;空白区域为自由栅格,即可航行的安全区域。

图1 扩展安全区域示意

图2 格栅化海图示意
2 航线规划数学建模
避浅航线规划的目的是避开浅滩,使船舶回归到计划航线。在避开浅滩的整个过程中要尽可能地使航行路径最短、转向点数目最少,并且以航道作为避浅航线的范围标准,结合船舶的实际航行情况,考虑船舶航向的变化,对船舶的转向角度和转向点的数目进行数学约束,并建立相关的数学模型。[9]设规划后航线的转向点序列为(P1,P2,P3,…,Pn),则
(2)
s.t.PiPi+1∩Bj=∅,i∈R;j∈R
(3)
θ≤90°
(4)
h≥hmin
(5)
式(2)~式(5)中:式(2)为规划后航线的距离是最短;式(3)为相邻转向点间的连线不与海图环境内的浅滩区域或者其他障碍区域相交,其中B为不同浅滩区域或者障碍物区域的集合;式(4)为船舶航向角度的改变不能超过90°;式(5)为对浅滩区域或者障碍物的扩展至少达到安全距离的要求。
3 航线规划
3.1 鱼群算法原理
3.1.1鱼群算法简介
影响鱼群觅食的主要原因是环境中的食物浓度,人工鱼群模拟自然界中鱼群的觅食、聚群、追尾以及随机等行为,通过这些行为在搜索域中寻优,从而达到优化的目的。模拟鱼群的行为见图3,假设一条人工模拟鱼的位置位于Q,其视野范围为Visual,Qn1、Qn2为视野内其他鱼的位置,前进一次的步长为Step,位置Qu为某时刻的视点所在位置:如果该位置的食物浓度高于当前位置,则向前前进一步,到达位置Qnext;如果位置Qu的浓度比当前位置Q的食物浓度低,则继续巡视视野内的其他位置。巡视的次数越多,则对视野内的状态了解越全面,有助于做出相应的判断和决策。[10]
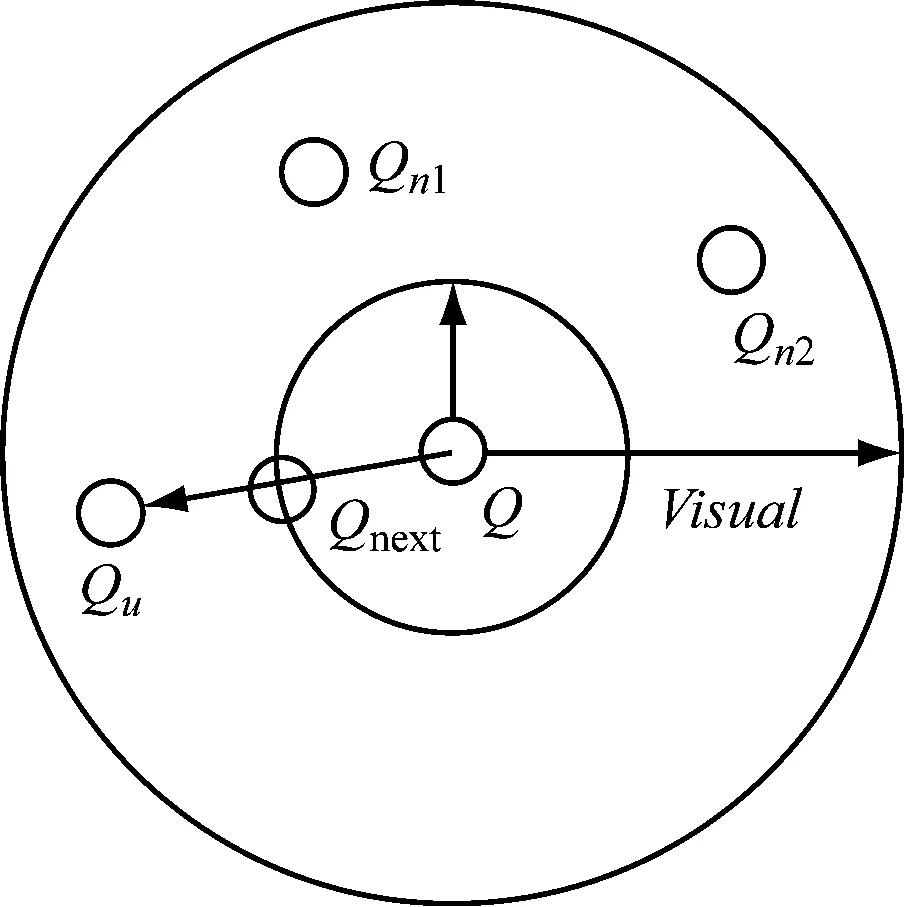
图3 人工鱼的视野和移动步长

(6)
(7)
式(6)~式(7)中:r是[-1,1]区间的随机数,允许存在一定的不确定性,可用于摆脱局部最优,从而实现寻找全局最优。
3.1.2鱼群行为描述[11]
(1) 觅食行为:这是鱼群最为基本的一种行为,是趋向于食物的一种活动;一般可认为通过感知环境中食物的浓度来选择运动趋向,在航线规划过程中,食物浓度表示路径长度值,浓度越大,路径长度越小。
(2) 聚群行为:鱼群在觅食和躲避敌害的时候通常是以聚集成群的形式进行的,人工鱼群的聚群行为表示鱼群会向食物浓度更优且在视野内并不拥挤的方向移动。
(3) 追尾行为:当某一条或几条鱼发现食物时,他们附近的鱼会尾随而来,进而更远处的鱼也会尾随而来。
(4) 随机行为:鱼群在水域中自由游动,更大范围地寻找食物或者其他鱼群,随机行为是人工鱼群算法中的一种缺省行为,当鱼群的其他行为无法找到更优解时,利用随机行为去寻找新的解。
3.2 航线规划鱼群算法的实现
鱼群算法的目的是寻找到食物浓度最高的位置以实现优化。在航向规划过程中,设鱼群的状态为X,食物浓度为Y,其中X记录一条完整的路径结果,如果路径的起点为A0=(x0,y0),终点为AZ=(xZ,yZ),则X[12]可表示为
X=A0A1…AZ=(x0,y0)(x1,y1)…(xZ,yZ)
(8)
式(8)中:Z为航线规划的节点数目,其本身的数字大小与鱼群算法优化后的人工鱼状态X有关。
在航向规划的过程中,为保证船舶能避开浅滩,且能返回到原始的计划航线,初始点A0与终止点AT是不变的,改变的是这两点间的其余转向点,鱼群算法优化的根本是调整其他路径点以找到最优的路径。
鱼群算法的实现主要是对鱼群行为的实现,在进行算法实现之前,首先设点相关参数符号,设定鱼群的个体大小为N,人工鱼移动的最大步长为Step,人工鱼的视野范围为Visual,觅食行为最大尝试次数为try_number,最大迭代次数为Max,最大拥挤程度为δ,gen记录迭代的次数,初始gen=1,r为[-1,1]区间的随机数,人工鱼个体之间的距离定义为d,则人工鱼群算法实现的流程见图4。
鱼群算法在得到初始化后,会优先执行聚群或追尾行为。图4中的聚群与追尾行为均包含觅食和随机行为:当鱼群的条件不满足执行聚群或追尾的触发条件时,会执行觅食行为;如果觅食行为得不到更优解,会进行随机行为;每一条鱼完成路径搜索后会加入到路径列表,完成全部迭代过程,确定最优解。
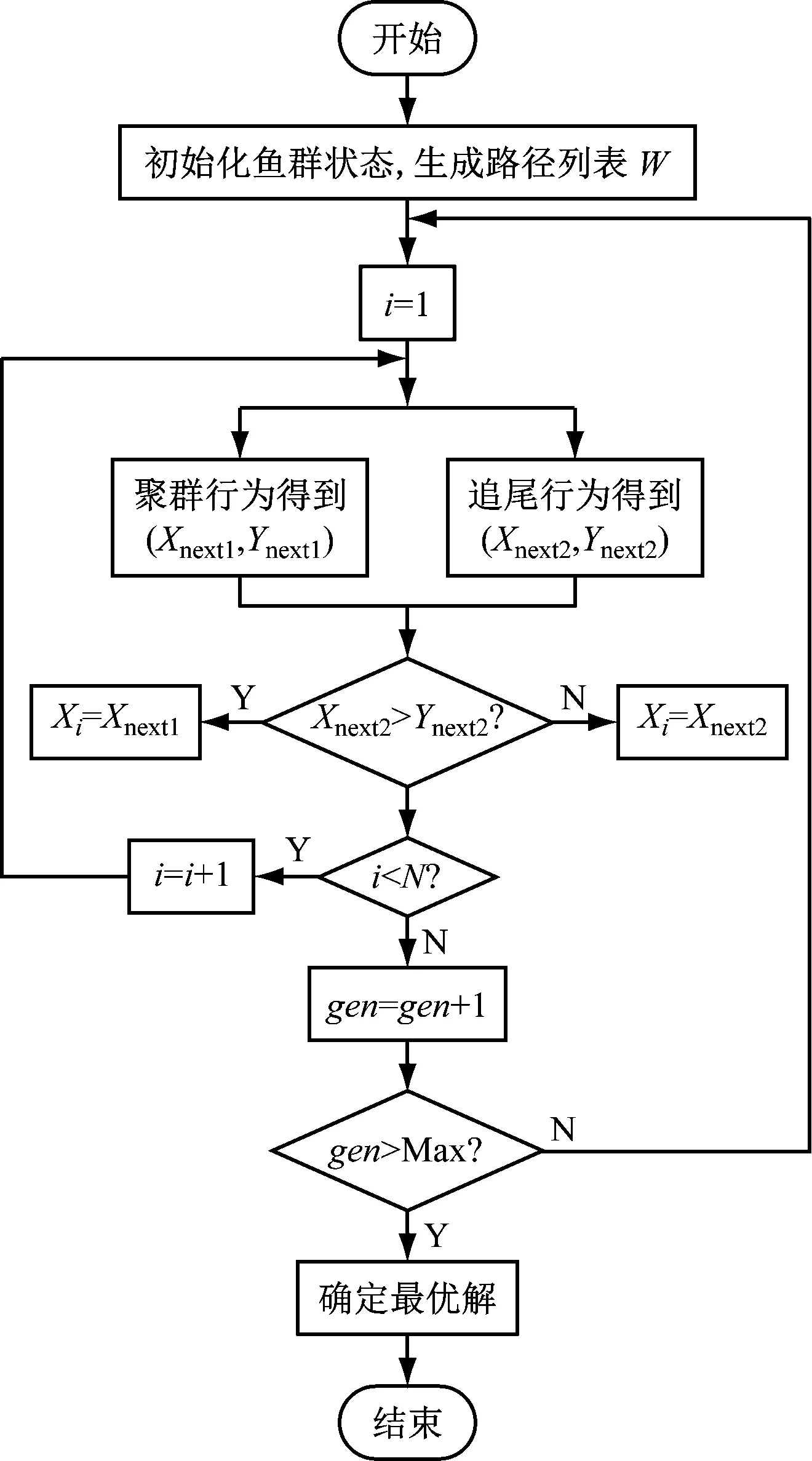
图4 鱼群算法流程
3.2.1觅食行为
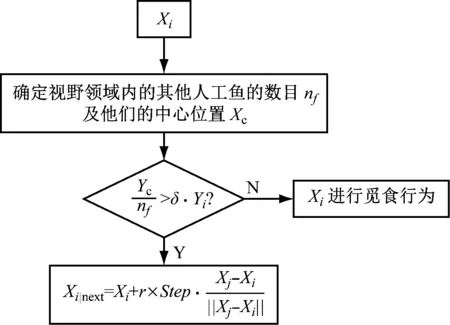
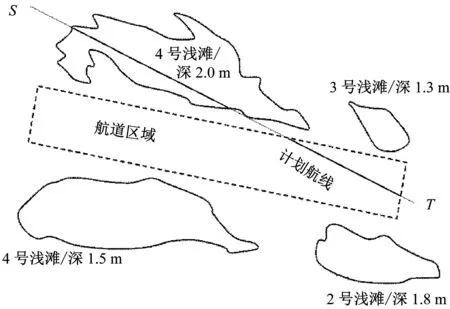
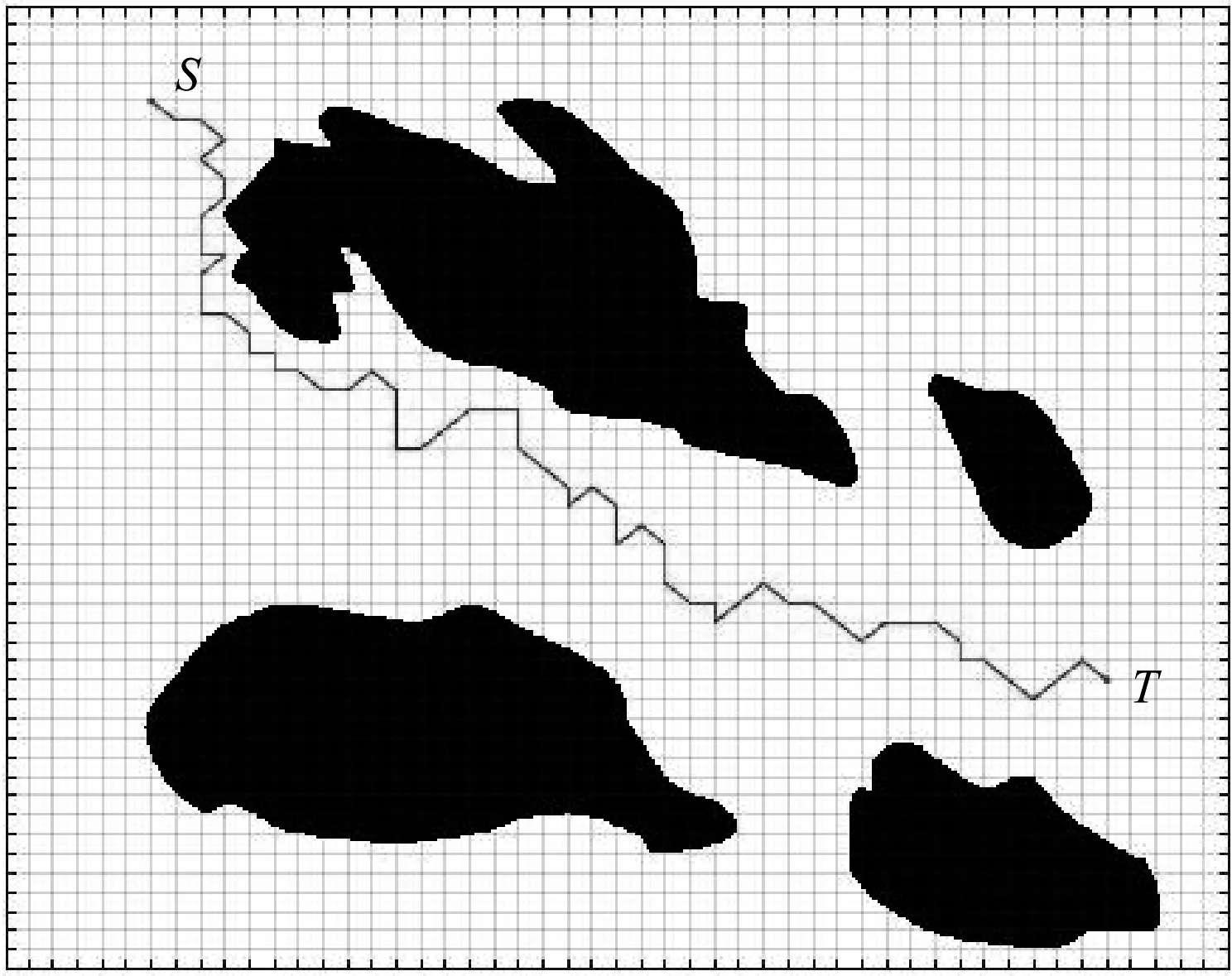
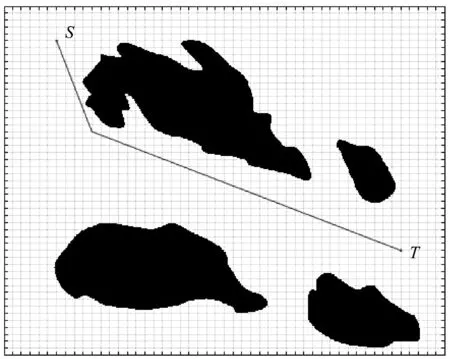
设人工鱼群的当前状态为Xi,在其感知范围内随机选择下一个Xj,在求算路径规划问题中,状态的改变是对其内部路径点的调整:若食物浓度Yi 图5 觅食行为过程 3.2.2聚群行为 设人工鱼当前的状态为Xi,根据其Visual的限制,搜索视野内其他人工鱼,确定视野内其他人工鱼的数目为nf,这些人工鱼的中心位置为Xc,食物浓度为Yc,如果Yc/nf>δ×Yi,这表明其他鱼群的中心位置有较多的食物,并且不太拥挤,则该人工鱼向视野内其他鱼群学习,朝中心位置方向前进一步,否则执行觅食行为。聚群行为过程见图6。 图6 聚群行为过程 3.2.3追尾行为 设人工鱼当前的状态为Xi,根据其Visual的限制,搜索视野内其他人工鱼,设视野内其他人工鱼的数目为nf并找到其中食物浓度最大的人工鱼,设该人工鱼的状态为Xk,食物浓度为Yk,如果Yk/nf>δ×Yi,这表明状态为Xk的人工鱼据有较高的食物浓度,并且不太拥挤,则人工鱼Xi朝人工鱼Xk方向前进一步,否则执行觅食行为。追尾行为过程见图7。 图7 追尾行为过程 3.2.4随机行为 随机行为的实现是在人工鱼的视野范围内随机选择一个状态位置,并朝这个位置前进一步,作为觅食行为的缺省行为,设人工鱼当前的状态为Xi,下一个位置为Xi|next,则随机行为为 Xi|next=Xi+r×Step (9) 栅格法将海图环境分解成同等大小的栅格后,人工鱼群算法利用不同的栅格信息规划航线,通过这种方式生成的原始航线虽然能满足式(2)、式(3)和式(5)的约束,但会呈现出锯齿状,不能完全符合航线规划的基本要求。为满足船舶航线规划中转向点尽可能少的航行习惯及式(4)中的约束条件,需要对生成的原始航线作进一步的调整,从而满足上述要求。 路径调整的思路为:取优化后的路径点,采用回溯的方式,将离终点最近的点与终点相连,判断连线是否穿越浅滩区域,若不穿越,则放弃该点,按照从终点到起点的方向,使下一个点与终点相连进行判断,直到出现一点与终点相连穿越浅滩区域,则记录该点前一点为转向点,再以该转向点为终点,继续回溯,直到达到起点为止。通过这种方式,在保证点与点之间的航线不穿过浅滩区域的情况下,尽可能地平滑航线,这样既能减少转向点,又能控制转向角度不会过大,从而满足式(4)中的约束条件。具体的航线调整流程[13]见图8。 图8 航线调整流程 通过人工鱼群算法最终输出人工鱼的最优状态X,X存贮的路径点用A表示,如式(8)所示。路径矩阵W本身包含起点A0与终点AZ,所添加的转向点均插入到起点与终点之间,最终输出矩阵W,完成航线调整。 根据国内浅滩水域的实际情况,模拟船舶航行环境见图9,试验假设船舶吃水为2.5 m,富余水深为0.5 m,由图9可知:计划航线穿过了4号浅滩,该处浅滩的水深为2.0 m,小于船舶的吃水数据,表明该计划航线存在搁浅危险。[14] 利用MATLAB软件提取船舶航行环境建立的模型见图10,其中黑色区域为已进行安全距离扩展后的浅滩区域,并进行格栅处理。为获得一定精度以及适合的计算速度,将模拟航行环境分成50×50个小格,其中点S和点T分别为需航线规划的起点和终点。 对MATLAB建立的环境模型利用人工鱼群算法规划航线,图中锯齿状的实线是规划后的结果,见图11。 图9 航行水域 图10 MATLAB模型 图11 人工鱼群算法航线规划结果 利用航线路径调整的思想重新生成航线见图12,经过调整,航线内仅剩1个转向点,且符合船舶转向时转向角度<90°的限制条件。 将利用MATLAB软件模拟得到的转向点添加到海图环境中,最终得到的航线规划见图13。图13中:黑色实线为规划后的航线;点S为航线的起点;T为航线的终点。转向点如图13所示。 图12 调整后的航线 图13 航线生成示例 为实现船舶避浅航线规划,依次从建立环境模型、人工鱼群算法航线规划以及航线路径调整3个阶段进行研究。首先利用栅格法对选取的海图环境建立模型,提取其中浅滩区域和障碍区域信息,进行安全距离扩展;在已建立的环境模型上利用人工鱼群算法,得到初始规划航线;随后利用航线调整原则对已优化的航线进一步进行调整,减少转向点,满足约束条件。 通过仿真试验可得到:利用人工鱼群算法能准确实现船舶避浅,并且满足海上航行的一般要求。与传统的VTS值班员根据自身经验指导船舶避浅的做法相比,基于人工鱼群算法的航线规划更具科学性,在一定程度上减少VTS值班员的工作量。但是,该算法考虑得并不全面,没有顾及周围动态船舶及天气的影响,这些因素会在今后做出进一步的研究。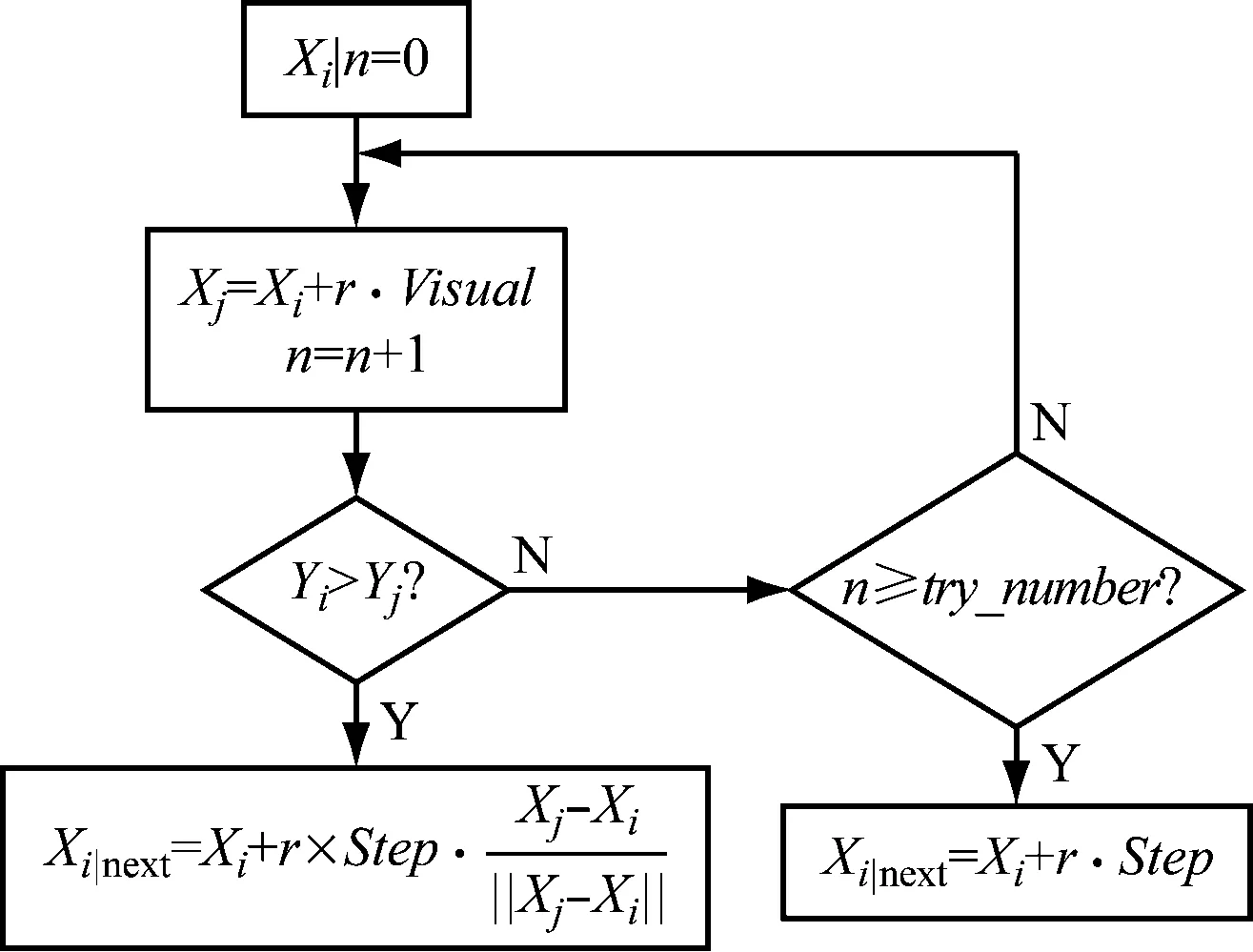

3.3 航线调整

4 算法模拟


5 结束语
