巧用面积原理解决三角形中的一类定比分点问题

广东省中山纪念中学(528454) 邓启龙

三角形中,有一类常见的定比分点问题.

题目1 如图1,P为△ABC内任意一点,直线AP,BP,CP分别交边BC,CA,AB于点D,E,F,若则分别为多少?

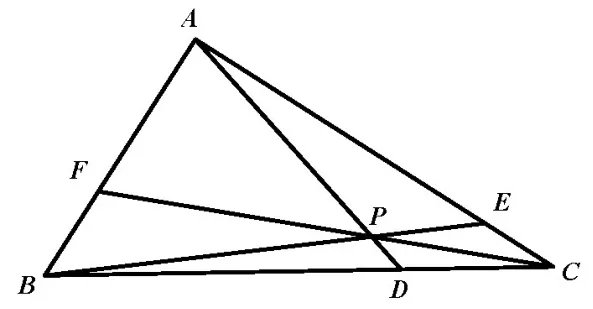
图1

笔者经过探究,通过巧妙地利用面积原理,找到了这些比例之间的等式关系.利用这些等式,已知其中任意两个比例,可快速求出其他四个比例.

设△BPC,△CPA,△APB的面积分别为S1,S2,S3,分别为k1,k2,k3,分别为t1,t2,t3.

结论1k1k2k3=1.

证明由面积原理和比例性质得

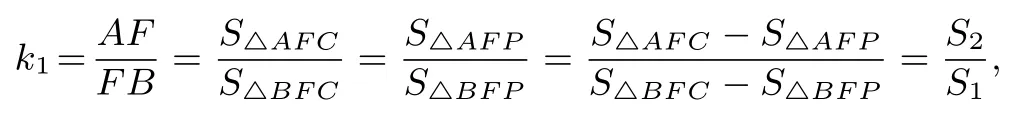
结论1 即是平面几何中著名的塞瓦定理.由结论1 可得,已知k1,k2,k3中的任意两个,可推出第三个.

结论2t1+t2+t3=1.

证明由面积原理和比例性质得

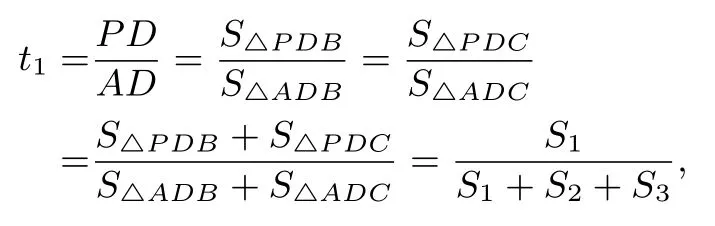
同理可得t2=所以t1+t2+t3=1.

由结论2 可得,已知t1,t2,t3中的任意两个,可推出第三个.

结论3S1:S2:S3=1:k1:k1k2=t1:t2:t3.

证明由结论1 的证明得S1:S2:S3=1:k1:k1k2,由结论2 的证明得S1:S2:S3=t1:t2:t3,所以S1:S2:S3=1:k1:k1k2=t1:t2:t3.

结论4t1=

证明由结论3 得S1:S2:S3=1:k1:k1k2,所以t1=同理t2=

由结论1 和结论4 可得,已知k1,k2,k3中的任意两个,可推出t1,t2,t3.

结论5

证明由结论3 得S1:S2:S3=t1:t2:t3,所以

由结论2 和结论5 可得,已知t1,t2,t3中的任意两个,可推出k1,k2,k3.若已知k1和t1,由结论5 得t2=k1t1,于是若已知k1和t2,由结论5得于是若已知k1和t3,由结论2 得t1+t2=1-t3,由结论5 得解得于是综上所述,已知k1,k2,k3,t1,t2,t3中的任意两个,可推出其他四个.

结论1-5 给出了六个比例k1,k2,k3,t1,t2,t3之间的等式关系,利用这些等式,可有效解决本文开头提出的三角形中的定比分点问题.下面结合例题说明结论1-5 在三角形中的定比分点问题中的应用.

例1同题目1.

解由已知得k1=2,k2=3,由结论1 得由结论4 得所以

例2如图1,P为△ABC内任意一点,直线AP,BP,CP分别交边BC,CA,AB于点D,E,F,若则分别为多少?

解由已知得k1=2,t3=由结论4 得t3=得k3=由结论1 得k2=3,由结论4得所以

结论1-5 给出了六个比例k1,k2,k3,t1,t2,t3,以及面积S1,S2,S3之间的等式关系,利用这些丰富的结果可有效解决三角形中的定比分点问题,以及三角形内一点引发的与定比有关的其他问题.

例3如图1,P为△ABC内任意一点,直线AP,BP,CP分别交边BC,CA,AB于点D,E,F,证明：

证明由=k2得=k2+1,由=t1得所以由结论4 得t1=所以

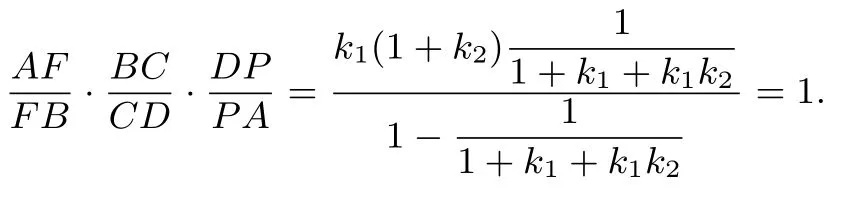
例3 即平面几何中著名的梅涅劳斯定理,利用结论4 立即证明该定理.

例4如图1,P为△ABC内任意一点,直线AP,BP,CP分别交边BC,CA,AB于点D,E,F,设△BPC,△CPA,△APB的面积分别为S1,S2,S3,证明：

证明由=k2得即,得

例4 即平面向量中著名的“奔驰定理”,本文通过巧妙地利用面积原理来证明该定理.