基于激光反射层析法的换能器声场测量技术及仿真研究

王伟印 陈 毅 王世全 杨柳青

(杭州应用声学研究所，浙江杭州 310023)

1 引 言

声场测量的目的是通过重建换能器的辐射声场，实现声场的可视化，进而对换能器的声学性能进行诊断与评估。对换能器辐射声场的测量，大多采用水听器进行，该方法实施简单，也最为方便。但由于水听器具有一定的物理尺寸，导致测量的空间分辨率受限。另外，水听器安装夹具的引入，会引起声波发生反射、衍射，对声场造成干扰，从而导致测量结果的准确性下降。

20世纪80年代，激光开始被应用于水声测量领域，先后出现了激光反射膜片法以及激光反射层析法等利用激光测量声场的方法[1-4]。由于采用激光进行测量，因此相比于水听器测量法，激光测量法具有对声场无扰动、空间分辨率高等独特优势。目前，国内对激光反射膜片法的研究已经较为成熟，而对激光反射层析法的研究并不多。且在对激光反射层析法的研究中，只研究了如何利用该方法重建声场，而如何利用该方法确定出声场中的绝对声压量值，在国内尚未见到相关报道。若能够精确确定出声场中的声压量值，则可以扩大激光反射层析法的应用范围，将其应用到换能器的发送响应以及水听器校准等方面。

本文主要对激光反射层析法在换能器辐射声场测量中的应用进行了研究，分析了激光反射层析法的测量原理，通过将激光反射层析法的数学理论与实际声场测量、声光效应相结合，对声场中绝对声压量值的定值公式进行了梳理与推导。在此基础上，对激光反射层析法进行仿真计算，验证激光反射层析法确定声场中绝对声压量值的可行性。

2 激光反射层析法的数理基础研究

2.1 Radon变换与反变换

1917年，奥地利数学家J.Radon提出了Radon变换与反变换，它是图像处理中的一种重要研究方法，为一大类图像重建问题提供了一个统一的数学基础[5]。

Radon变换的原理示意图如图1所示，假定xy平面内具有某种物理性质的二维分布函数f(x,y)，l为平面上的一条直线，其在xy平面内的位置由式(1)确定

xcosθ+ysinθ=t

(1)

式中：θ——直线l的法线与x轴的夹角；t——原点到直线l的距离。

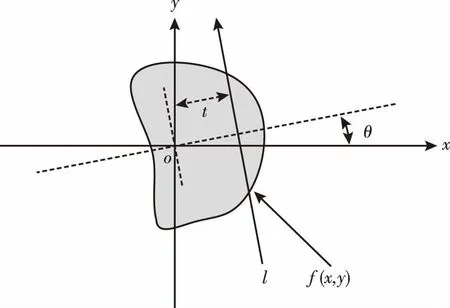
图1 Radon变换示意图Fig.1 Radon transformation

则二维函数f(x,y)的Radon变换定义为f(x,y)沿着直线l的线积分Pθ(t)，定义式为

(2)

若沿着直线l的方向建立s轴、l的法线方向建立t轴，则可将(t,s)作为新的坐标系，如图2所示。

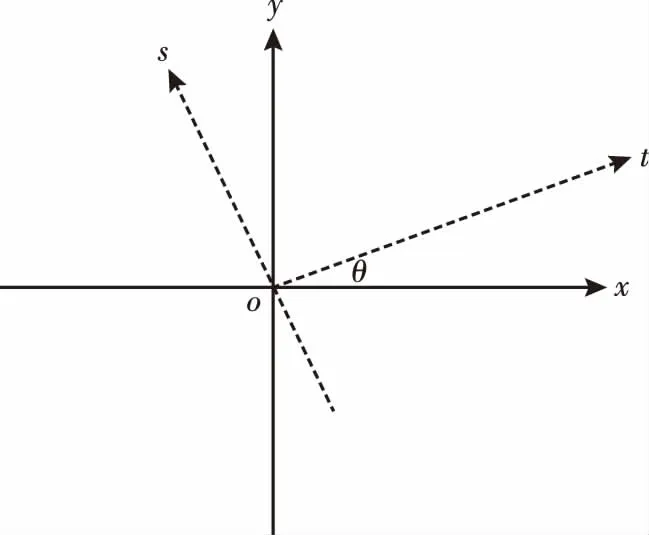
图2 新旧坐标关系示意图Fig.2 New and old coordinate relationship

(t,s)坐标系与(x,y)坐标系之间的关系可用式(3)表示

(3)

则f(x,y)的Radon变换可表示为

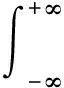
(4)

当θ固定时，改变t，使t取所有不同的值，即可得到二维平面函数f(x,y)在θ方向上的投影值，然后改变θ，使θ取0到π内的所有值，即可得到f(x,y)在所有θ方向下的投影数据，如图3所示。

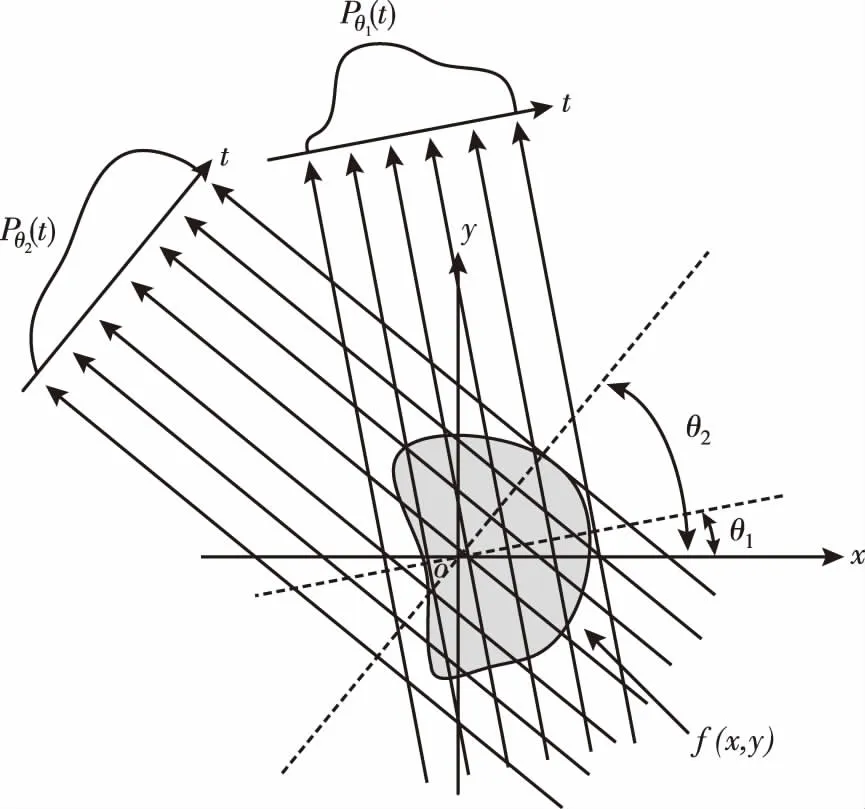
图3 改变θ和t后的f(x,y)投影示意图Fig.3 Projection of f(x,y) after changing θ and t

2.2 傅里叶切片定理

傅里叶切片定理是推导重建算法的基础，它指的是：二维分布函数f(x,y)在θ方向下投影的一维傅里叶变换等于f(x,y)二维傅里叶变换的其中一个切片，该切片与u轴成θ角度，且通过坐标原点，如图4所示。

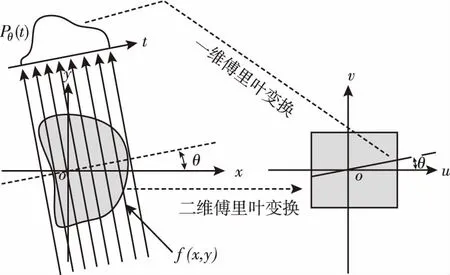
图4 傅里叶切片定理示意图Fig.4 Fourier slice theorem

傅里叶切片定理的意义在于，通过对投影进行一维傅里叶变换，可以得到原始图像的二维傅里叶变换，从而可以按图5所示的流程重建出原始图像。

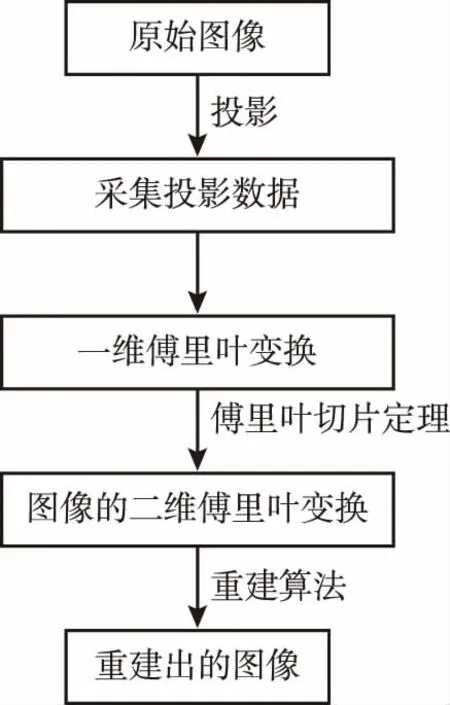
图5 重建图像流程图Fig.5 Reconstruction image flow

2.3 滤波反投影算法

滤波反投影算法(Filter Back Projection，FBP)是求解二维傅里叶逆变换的一种数学处理方法，也是图像重建中应用最广泛的一种算法[6]。

滤波反投影算法主要包括滤波和反投影两部分，对投影数据的滤波通过式(5)进行

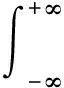
(5)

式中：Qθ(t)——滤波后的投影数据；Sθ(ω)——投影数据Pθ(t)的一维傅里叶变换；|ω|——滤波器的频率响应函数。

当采用Ram-Lak滤波器进行滤波时，式(5)的离散形式可写为

(6)

式中：n=0，1，2，，N-1，N——投影线的条数；τ——投影采样间隔；h(nτ)——Ram-Lak滤波器响应函数。

离散形式下，Ram-Lak滤波器的响应函数如式(7)所示

(7)

为提高运算速度，可将式(6)变换到频域进行计算，变换后的表达式为

Qθ(nτ)=τ×IFFT{FFT[Pθ(nτ)]×FFT[h(nτ)]}

(8)

式中：FFT——傅里叶变换；IFFT——傅里叶逆变换。

根据二维傅里叶逆变换公式，待重建的二维分布函数f(x,y)在极坐标形式下可写为

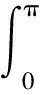
(9)

式(9)即表示对滤波后的投影数据Qθ(t)进行反投影的过程，由式(5)和式(9)实现的图像重建算法即为滤波反投影算法。

通过式(7)～(9)，可得待重建的二维分布函数的离散形式为

(10)

式中：k—— 0°～180°范围内的投影角度步进数。

3 激光反射层析法测量原理

3.1 测量原理

激光反射层析法的测量原理图如图6所示，待测换能器被固定在运动回转装置上，调节待测换能器，使其辐射面竖直向下、声轴与z轴重合。激光测振仪发出的激光光束与换能器声轴方向垂直，入射到反射镜面后沿原路径返回到激光测振仪[7]。

图6 激光反射层析法测量换能器声场示意图Fig.6 Laser reflection tomography for measuring the acoustic field of a transducer

激光束经过声波作用的区域时，由于该区域内媒质的折射率发生变化，导致激光束受到声波的调制作用[8]。当换能器在角度θ下沿x轴方向运动时，根据声光效应，激光测振仪的输出信号可表示为

(11)

式中：n1——水介质的光弹系数；ω——角频率；dy——声场中沿激光传播路径的微分；p(x，y)——声场中(x,y)位置处的声压。

对比Radon变换的定义可以发现，激光测振仪的输出v(x)对应于声压分布p(x,y)在x方向上的投影。因此，通过测量不同角度θ下得到的激光测振仪输出信号v(x)，对其作Radon反变换，即可求得换能器的声场分布函数p(x,y)[9]。

通过式(8),(10),(11)可得，待测声场中绝对声压量值的计算公式为

×FFT[h(nτ)]}}

(12)

式中：M——换能器在0°～180°范围内的旋转次数。

3.2 声光效应

声波是一种弹性波，它在液体中传播时，会使液体介质产生相应的弹性形变，从而激起液体介质中各质点沿着声波传播的方向振动，引起液体局部密度呈现疏密相间的变化。

在小振幅声波(通常小于0.1MPa)作用下，液体的折射系数与液体密度的变化成线性关系，可表示为

(13)

式中：n0——不存在声波时水介质的折射系数；n1——水介质的光弹系数；n(x,t)——液体在声波作用下的折射系数。

所以，声波的存在会导致介质的折射系数发生改变，引起激光束传播路程的变化，从而建立起光程变化速度与换能器声场分布之间的联系。

4 激光反射层析法仿真研究

设在无限大平面障板上嵌有一个半径为a的圆面活塞换能器，换能器静止时的辐射面与障板表面位于同一平面上。当活塞以速度u=uaejωt振动时，换能器将向障板前面的半空间辐射声波。以活塞中心为坐标原点，活塞所在的平面为xOy平面，过坐标原点且垂直于活塞平面的直线为z轴，建立坐标系如图7所示。

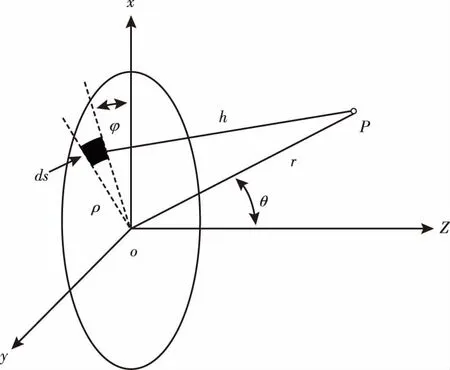
图7 圆面活塞换能器辐射示意图Fig.7 Schematic diagram of circular piston transducer radiation

由瑞利公式可知，活塞声源在空间任意一点处的声压可通过式(14)计算得出

(14)

式中：ρ0——声场中传播介质的密度；c0——声场中传播介质的声速；k——波数；h——面元ds到点P的距离。

取圆面活塞换能器辐射面半径a=2cm，工作频率f=1MHz，距辐射面距离z=3cm。根据式(14)，对换能器的近场声压分布进行仿真，得到的原始声场即换能器的近场声压分布三维及平面示意图如图8和图9所示。

图8 圆面活塞换能器的近场声压分布三维示意图Fig.8 Schematic 3D view of near-field acoustic pressure distribution of a circular piston transducer

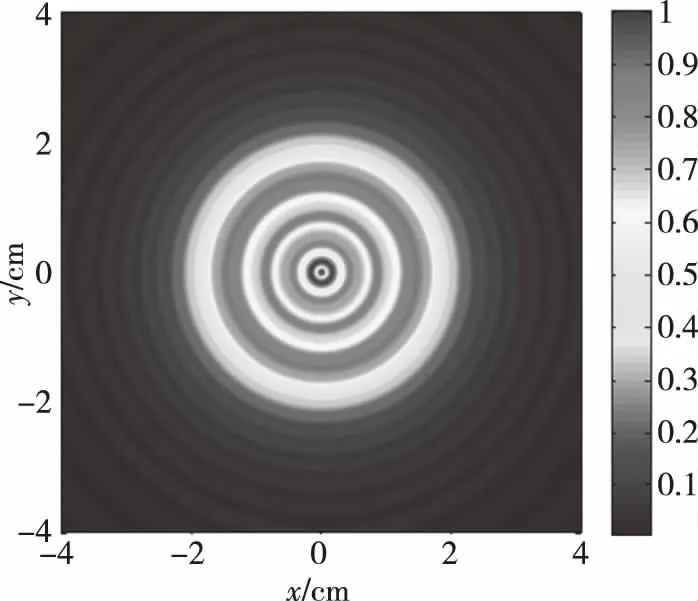
图9 圆面活塞换能器的近场声压分布平面示意图Fig.9 Near-field acoustic pressure distribution of a circular piston transducer

根据激光反射层析法的测量原理，设定测试步骤如下：在一个角度下，激光完成线性扫描后，将换能器旋转至新的角度，在新的角度下继续进行线性扫描，直至完成180个角度下的扫描投影；设定测试条件如下：测试在以换能器声轴为对称轴的(8×8)cm的平面上进行，激光在一个角度下进行457次扫描，扫描的步进间距为0.017 5cm，换能器在0°～180°范围内进行旋转，旋转步进间距为1°。根据设定的测试步骤及测试条件，在Matlab中编写程序，对仿真出的声场进行Radon变换，得到的Radon变换结果如图10所示。

图10 仿真得到的Radon变换结果示意图Fig.10 Radon transform result obtained by simulation

运用滤波反投影算法，对得到的投影数据进行Radon反变换，得到的声场重建结果如图11所示。

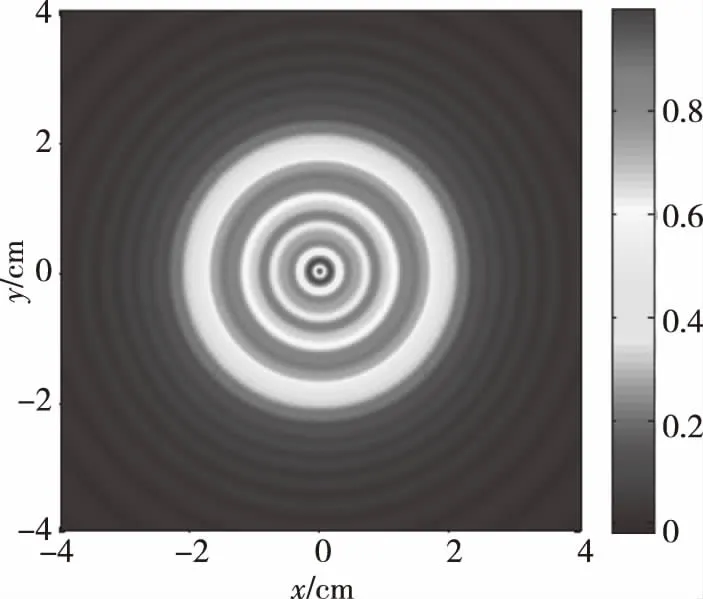
图11 通过Radon反变换得到的声场重建结果示意图Fig.11 Acoustic field reconstruction results obtained by radon inverse transformation

取位于原始声场与重建声场中心线上的声压数据作对比，得到的对比结果如图12所示。

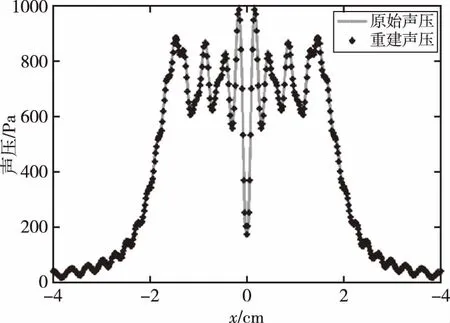
图12 原始声场与重建声场的声压数据对比曲线图Fig.12 Comparison of original acoustic field and reconstructed acoustic field

由图9和图11可以看出，利用激光反射层析法可以精细地重建出换能器的声场分布，重建出的换能器声场能够清晰地分辨出旁瓣位置，声场特征与原始声场基本一致。通过原始声场与重建声场的声压数据对比可以看出，激光反射层析法重建出的绝对声压量值与原始声压量值吻合良好，表明激光反射层析法能够准确地确定出声场中的绝对声压量值。

5 结束语

本文对激光反射层析法重建换能器声场分布的原理及方法进行了详细阐述与推导，并通过仿真计算，验证了激光反射层析法测量换能器辐射声场分布及声场中绝对声压量值的可行性，为换能器的声场重建及声压测量提供了一种准确、有效的方法。后期有待开展相关实验，对激光反射层析法进行进一步的验证，并研究信噪比、扫描步进间距以及投影角度数等因素对声场及声压重建效果的影响。