多导弹协同目标参数估计的EKF设计

花文华，张金鹏,2，张拥军

(1.中国空空导弹研究院，河南 洛阳 471009;2.航空制导武器航空科技重点实验室，河南 洛阳 471009)

0 引言

将一类仅可提供目标方位角量测的拦截导弹作为研究对象。仅有角度量测情况下的目标跟踪问题的研究成果可用于该类型拦截导弹滤波器的设计。然而，在目标机动不确定性和量测噪声等因素的影响下，即使采用先进的滤波器，如粒子滤波等，拦截高机动目标的性能仍将受限于滤波器的延迟和跟踪精度的影响，同时滤波器越先进，往往也越复杂，在弹上实现也是一个问题。一种改进目标跟踪精度，从而改进拦截性能的方法是增加量测量。这一方法通常需要改变导弹的硬件，如采用多模导引头等，会较大程度的增加导弹的成本和复杂度，且工程化的多模导引头在国内仍属技术难点。另一种方式是采用其他信息源的信息，如地面跟踪雷达。这一要求需要地面或机载跟踪雷达持续的向拦截导弹传送目标信息，会限制跟踪雷达的运行，且影响导弹的自主性，同时跟踪雷达的跟踪精度会随着探测距离的增加而显著下降。对于拦截一些高价值目标的情形，如拦截弹道导弹、隐身战机、预警机等，往往会发射多枚导弹以提高命中概率，但拦截导弹之间并不存在协同或信息共享，因此多弹同时拦截情况下的可用信息并未得到充分利用。

多导弹协同易于构建更加有利的目标拦截态势，从而改进制导性能并降低控制量要求，多弹协同也可用于饱和目标防御、限制目标机动概率、诱骗目标和增强对目标的可观测性等方面[1-5]。本文提出一种基于扩展Kalman滤波器(extended Kalman filter,EKF)[6-9]的多导弹协同滤波方法，通过坐标转换和滤波器量测方程的建立，实现导弹间量测信息的共享，从而改进估计性能。

1 数学建模

1.1 系统状态模型

针对多枚导弹攻击一个目标的拦截情形进行建模，导弹采用设定的制导律，彼此在制导上不存在协同，仅进行信息共享。假设导弹是滚转稳定的，可近似分解为垂直和水平2个平面分别进行研究，且结果是类似的。垂直平面的弹目相对运动关系如图1所示。

图1 平面弹目相对运动关系Fig.1 Planar engagement geometry

图1中Mi和Mj分别表示拦截导弹i和j，T为目标，v，a和γ分别表示速度、加速度和航向角，下标m和t分别对应导弹和目标，Mi和目标间、Mj和目标间的相对距离分别采用ρmi和ρmj表示，相对应的视线角为λmi和λmj。

以导弹Mi为例，选取导弹自身的状态变量为

(1)

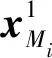
选取导弹关于目标的状态向量为

(2)

假设目标做常速运动，且具有一阶控制系统动态，式(2)相应的状态方程可以表示为

(3)

式中:

vρi=-[vmicos(γmi-λmi)+vtcos(γt+λmi)],
vλi=-vmisin(γmi-λmi)+vtsin(γt+λmi)；

(4)

τt为目标的控制系统时间常数；atc为加速度指令，是一个白噪声驱动的随机过程。

1.2 量测模型

假设拦截导弹安装有仅可提供角度量测的导引头[10-15]，可以提供相对目标的视线角度信息，该类型导引头具有低成本的优势。建立导弹Mi的量测方程为

zmi=γmi-λmi+wmi,

(5)

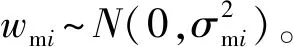
导弹Mj的量测方程也是类似的，结合图1，将Mj的量测方程写成导弹Mi的状态表示的形式：

(6)

导弹Mi和导弹Mj在同一个坐标系下，导弹Mj将自身的位置信息传输给导弹Mi用于构建量测方程，实现信息共享或协同滤波，则导弹Mi综合n个导弹信息的量测方程可表示为

(7)

导弹Mi相应增加了n-1个伪量测信息。采用EKF进行协同滤波器的设计，并假设噪声符合高斯分布。对于一些先进的滤波方法，如粒子滤波，并不受限于量测噪声的高斯特性要求。

2 协同扩展Kalman滤波器设计

2.1 滤波器的设计

扩展Kalman滤波器通过Taylor序列展开实现了对系统状态和量测量联合分布的高斯近似，从而将Kalman滤波器的适用范围扩展到了非线性系统领域。

EKF所采用的滤波模型为

xk=f(xk-1,k-1)+Qk-1，
zk=h(xk,k-1)+Rk，

(8)

式中：f和h为非线性函数向量,分别为系统动态模型和量测模型，分别与式(3)和式(7)相对应。

在给定量测z1 : k的条件下，状态xk的分布概率满足：

p(xk|z1 : k)=N(xk|mk,Pk)，

(9)

式中:mk和Pk分别为状态xk的均值和方差。

在每一个执行周期内，EKF都由状态预测和量测更新2个过程构成。相应于系统(3)的状态预测为

xk|k-1=f(xk-1,k-1).

(10)

相应的预测误差协方差矩阵为

(11)

式中:

Φk,k-1=eFxk·T,

(12)

(13)

式中：Fxk和Φk,k-1分别为状态方程(3)的Jacobian矩阵和状态转移矩阵；T=tk-tk-1为执行周期；Qd为系统噪声离散化后的误差矩阵，其大小与滤波器的响应速度相关。

在状态预测完成后进行量测更新，

xk|k=xk|k-1+Kk(zk-h(xk|k-1))，

(14)

式中：K为滤波器增益矩阵,由式(15)进行计算：

(15)

式中：Sk为滤波新息的协方差矩阵；Hx为量测Jacobian矩阵，满足：

(16)

对于导弹Mi，结合式(7)，可将式(16)展开为

(17)

(18)

(19)

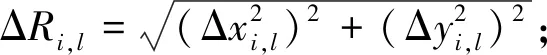
(20)

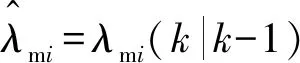
最后进行滤波器协方差矩阵更新，用于下一滤波周期预测误差协方差矩阵的计算：

(21)

将式(13)表示成式(22)的形式，进行可观性分析:

(22)

对于仅有视线角度量测的单枚导弹，Hx=(0，-1，0，0，0)，根据线性系统可观性判据，

(23)

式中:o21等矩阵参数不展开给出，但可以发现系统很容易满足rank{Om1}=5的条件，即系统是可观的，对于多导弹信息协同的情况，系统同样是可观的，且可观测性有所增强。

对观测方仅可提供角度测量的情况,文献[16-17]分别针对单传感器和多传感器对目标运动的可观测性进行了研究。文献[16]从几何方法、线性与非线性方法、数值分析方法等角度，对单传感器情况下的纯方位目标运动的可观测性研究成果进行了综述。文献[17]对多静止测向站系统的可观测性、定位方法进行了分析和研究，建立了纯方位多传感器系统目标定位问题的数学描述，并定量分析了系统的可观测性条件，指出多观测方与目标共线、多观测方位置不分辨、观测方测量时机选择不当等产生不良的拓扑结构会带来系统的不可观测。对于多观测方和目标同时运动情况下的可观测性研究较少，可以从不可观测拓扑构型分析和避免措施方面开展研究，从而满足多导弹的协同作战使用需求。

2.2 滤波器的初始化

假设所有的导弹都由同一机载或地面雷达进行初始化。图2给出了雷达R与导弹之间的平面相对关系。雷达与目标间的视线角和相对距离分别为λr和ρr，此外通过相关滤波技术还可以提供目标的航向角γt和加速度at信息。雷达的位置(xr,yr)是已知的，与初始信息(λr0,ρr0,γt0,at0)一同通过发射前任务加载或数据链信息传输给导弹。利用这些信息，导弹完成滤波器的初始化，其中弹目距离和视线角的初始化值为

(24)

(25)

图2 雷达与导弹的平面相对关系Fig.2 Planar engagement geometry between radar and missile

式中:

(26)

3 仿真结果及分析

系统状态的估计结果如图3～7所示。

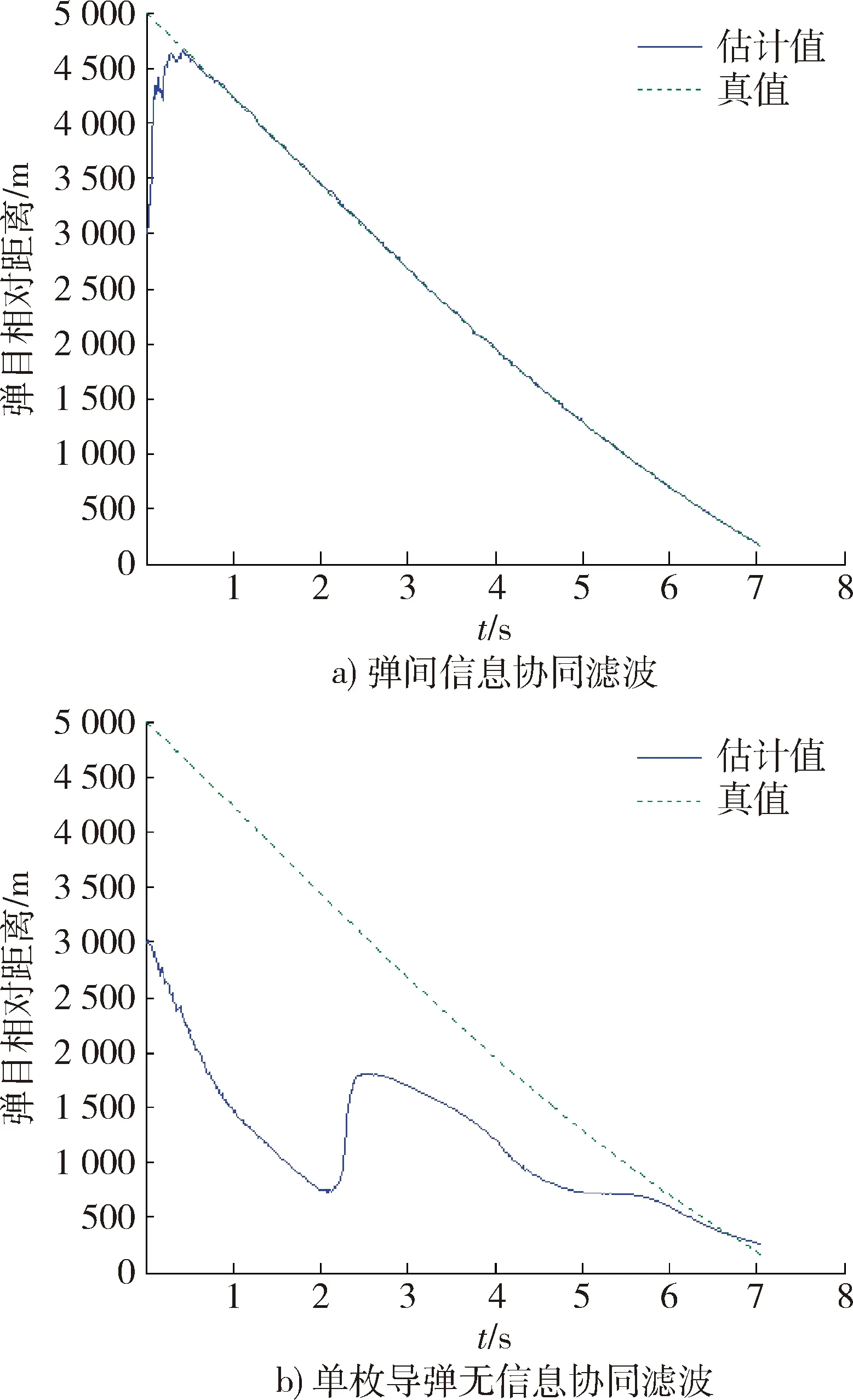
图3 弹目相对距离估计Fig.3 Estimation of range between missile and target

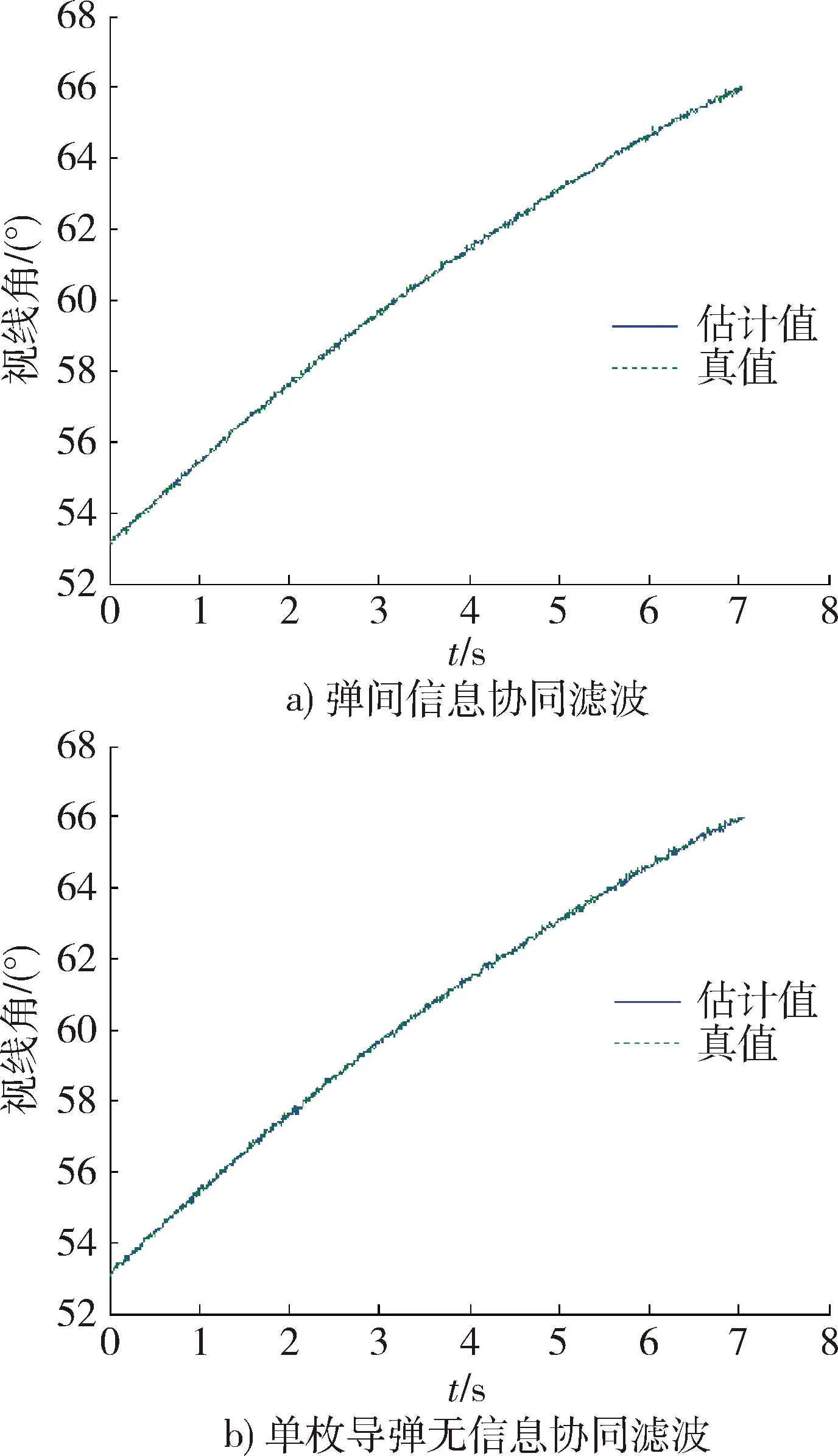
图4 视线角估计Fig.4 Estimation of line of sight angle

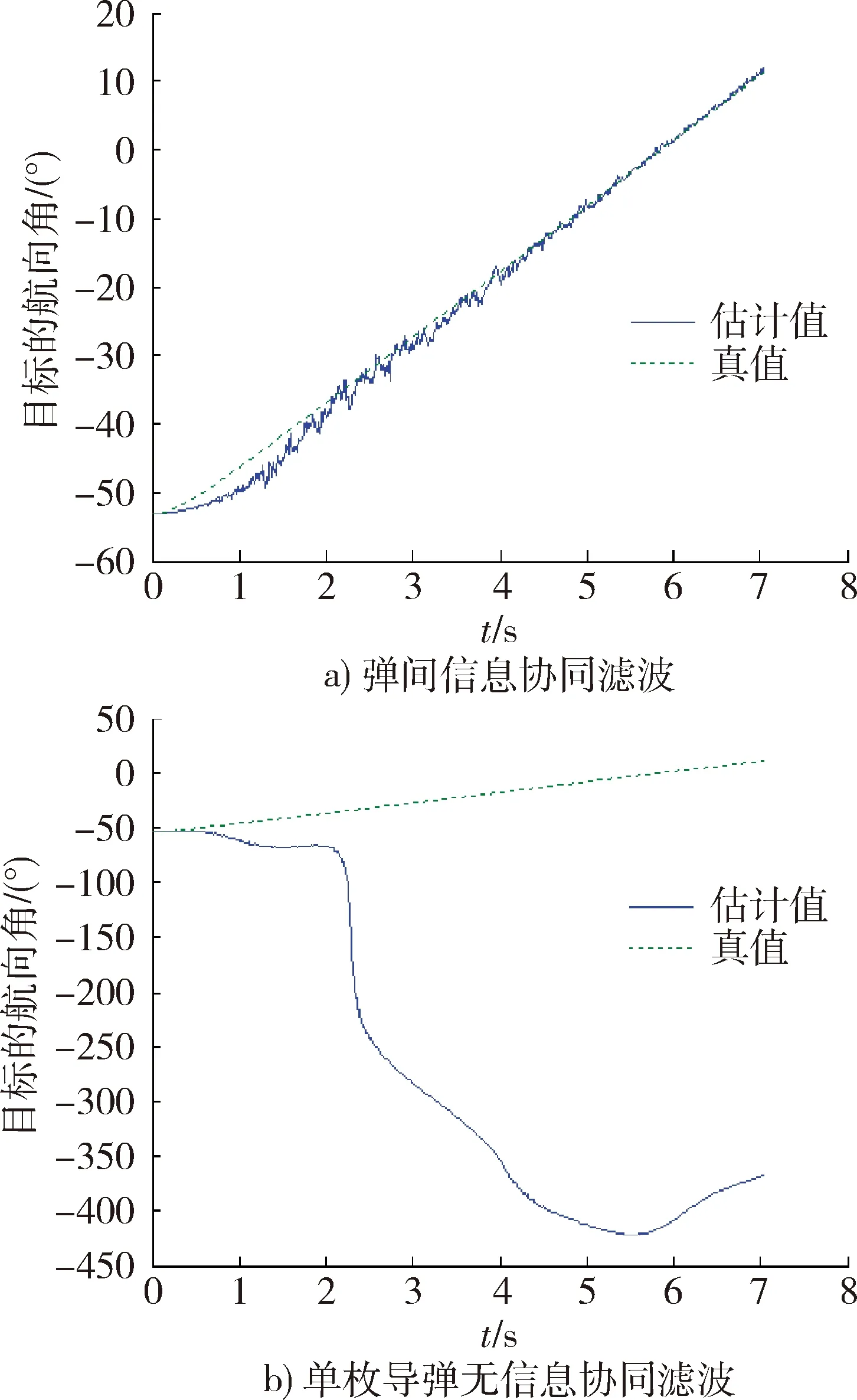
图5 目标航向角估计Fig.5 Estimation of flight-path angle

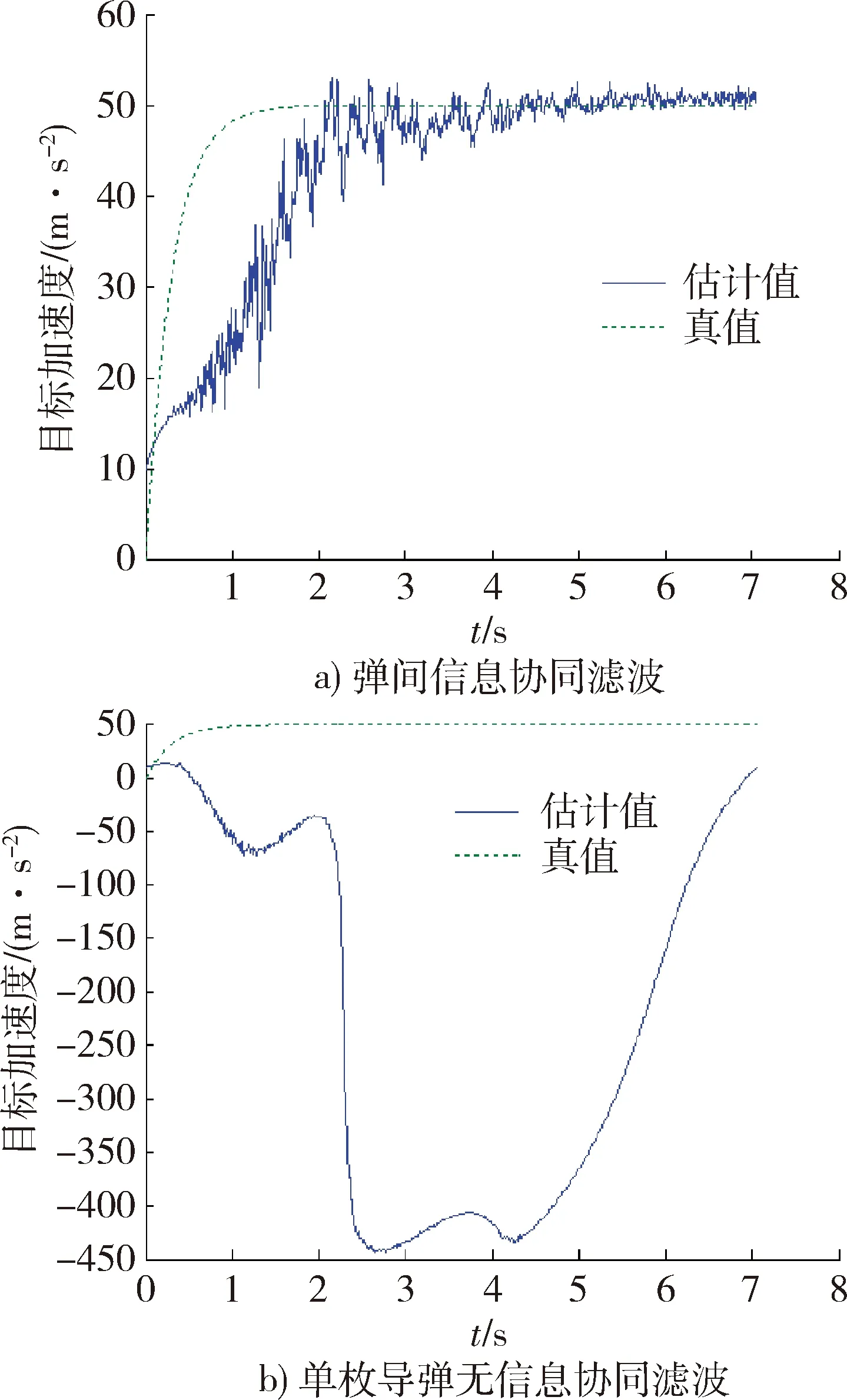
图6 目标加速度估计Fig.6 Estimation of target acceleration

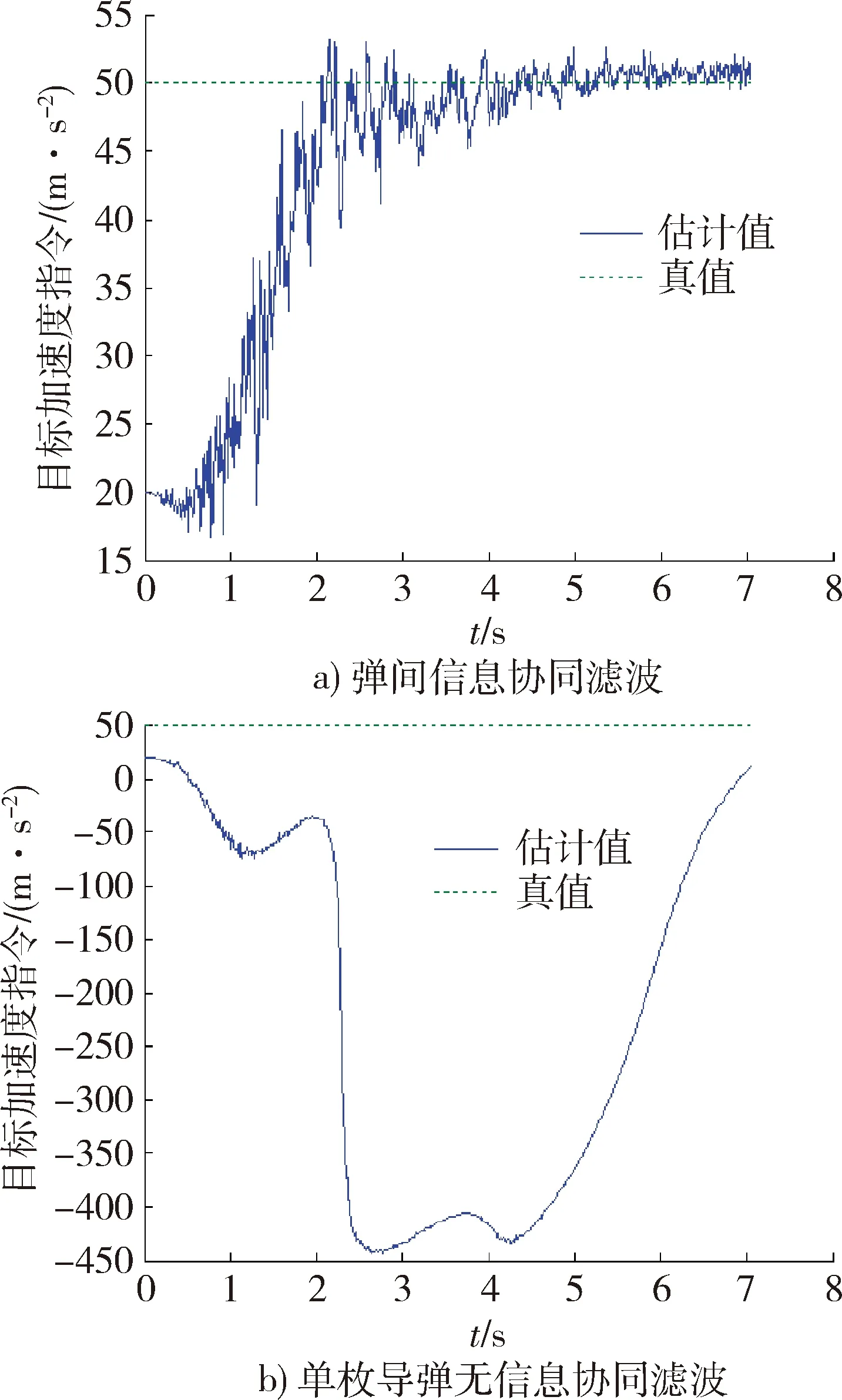
图7 目标加速度指令估计Fig.7 Estimation of target acceleration command

从图3～7中可以发现，在较大的初始弹目相对距离误差(2 000 m)下，单枚导弹的滤波器除与量测相关的视线角状态外，其他状态并不收敛，而在存在协同的情况下，由于可观测性增强，获得了较好的状态估计结果。由于是可观的，虽然在适当的初始条件下是可以实现状态收敛的，但仅有角度量测的单枚导弹滤波器对状态初值和估计误差协方差初值是较为敏感的，出现了发散现象。

图8～12进一步给出了2枚导弹信息协同的情况下200次Monter Carlo仿真的状态估计的统计，包括估计误差均值和1σ包络曲线。从图8～12中可以看出，各状态的估计误差都是收敛的。

图8 弹目相对距离估计误差统计，弹间协同Fig.8 Statistical estimation errors of range for cooperation missile

图9 视线角估计误差统计，弹间协同Fig.9 Statistical estimation errors of line of sight angle for cooperation missile

图10 目标航向角估计误差统计，弹间协同Fig.10 Statistical estimation errors of flight-path angle for cooperation missile

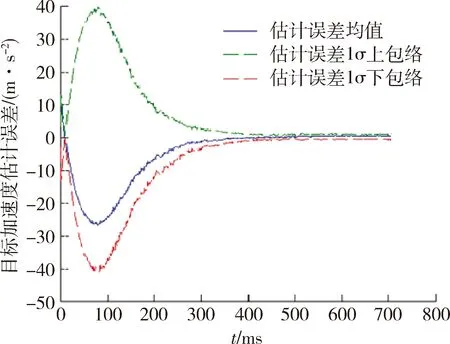
图11 目标加速度估计误差统计，弹间协同Fig.11 Statistical estimation errors of target acceleration for cooperation missile

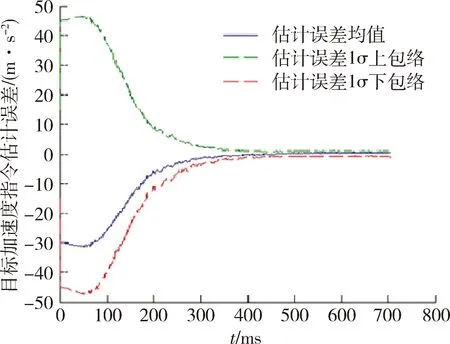
图12 目标加速度指令估计误差统计，弹间协同Fig.12 Statistical estimation errors of target acceleration command for cooperation missile

4 结束语

本文针对多枚导弹量测信息共享的情况，完成了基于EKF的多导弹协同滤波器的设计。相比于单枚导弹的情况，由于可观测性增强，在初始弹目相对距离误差较大的情况下，实现了对所有系统状态的较好估计，同时Monter Carlo仿真结果表明所有状态的估计误差都是收敛的，进一步表明了弹间协同滤波的优势。