基于渗流-损伤-应力耦合作用下考虑力学参数弱化的巷道围岩变形破坏分析*
2019-10-26孙琪皓马凤山赵海军冯雪磊
孙琪皓 马凤山 赵海军 郭 捷 冯雪磊
( ①中国科学院地质与地球物理研究所,中国科学院页岩气与地质工程重点实验室 北京 100029)
( ②中国科学院地球科学研究院 北京 100029)
( ③中国科学院大学 北京 100049)
0 引 言
随着人类对资源需求量的日益增加,能源开采逐渐向更深和更复杂的地层中进军,深部地质工程所面临的“三高和强扰动强时间效应”问题更加凸显,巷道围岩冒顶、帮缩、底鼓,分区化破裂,岩爆,突水等非线性物理力学现象更加突出( 何满朝,2014) ,开挖后的巷道处于更加复杂的地质力学环境当中,其变形和破坏过程往往是在多个物理场耦合作用下发生的结果( 周宏伟等,2005) 。谢和平等( 2015) 详细阐述了国内外关于深部与浅部的量化界定,何满朝等( 2005) 对深部和浅步情况下巷道开挖引起的力学差异进行了详尽分析,贺永年等( 2006) 分析了深部岩石工程研究中存在的若干问题,并揭示了巷道围岩断裂间隔分布的现象。周小平等( 2007) 研究了深部开采产生分区破裂化现象的机理,姜耀东等( 2004) 分析了深部巷道底鼓的不同类型和影响因素,并总结了深井软岩巷道底鼓的防治措施。刘高( 2000) 论述了高应力软岩的特点,总结了高应力软岩巷道的变形类型及特征,分析了开挖前后地应力变化对巷道稳定性的影响作用机理。李术才等( 2008) 通过对分区破裂化现象的现场监测,分析了深部围岩的破裂模式。还有众多学者通过现场测量、物理模拟实验、数值模拟等不同手段对巷道围岩稳定性机理进行了系统研究。
地下工程的安全问题常常与地下水的作用密不可分。自Biot( 1941) 进行三维固结问题的研究,奠定了流固耦合理论的研究基础后,学者对渗流-应力耦合问题做了大量理论和试验的研究工作,提出了一系列经验公式和理论模型,总体上可以分为等效连续介质模型、离散裂隙网络模型和双重介质模型。近年来,岩体内部结构的损伤效应引起了广泛的关注,损伤带来了更加复杂的耦合效应,据此学者提出了许多基于断裂力学和损伤力学的耦合理论。Shao et al. ( 2004) 建立了基于岩石微裂纹演化的各向异性损伤模型,并根据细观力学分析提出了岩石宏观力学参数及渗透张量与细观损伤之间的关系。Oda et al. ( 2002) 进行试验研究了岩石材料的相关力学参数与损伤变量,并考虑裂隙几何张量分析了岩石渗透性的变化规律。荣传新等( 2004) 根据弹塑性损伤理论、极值点失稳理论分别推导出了渗流作用下巷道围岩应力分布规律和巷道围岩的稳定性条件,并分析了突水事故发生的原因。卢应发等( 2007) 基于能量原理,通过Gibbs 自由能建立了一种正交损伤模型,并应用到流固耦合的研究中。郑少河等( 2002) 基于自洽理论,研究了考虑损伤断裂效应的岩体渗透张量演化过程,并建立了多裂隙岩体渗流损伤的理论模型。冯夏庭等( 2005) 通过自行研制的实验装置进行了应力-渗流-化学多场耦合的细观力学试验,对全过程显微和监测并对试验现象进行了分析。杨天鸿等( 2001) 引入了渗透突跳系数这一概念,提出了岩石破裂损伤过程中的渗流-应力耦合机制。朱万成等( 2009) 基于质量守恒和能量守恒定量,建立了考虑损伤的热-流-力耦合模型,并分析了水力损伤的作用机制。沈振中等( 2009) 基于无单元法建立了岩体水力劈裂过程中的应力-渗流-损伤耦合模型,并对具有初始裂纹的平面应力模型进行了裂纹扩展的耦合分析。贾善坡等( 2009) 提出了与塑性损伤演化和渗流相关联的Mohr-Coulomb 破坏准则,并采用该准则建立了考虑围岩损伤和渗透性动态演化过程的流-固全耦合迭代计算模型。赵延林等( 2010) 利用断裂力学和几何损伤力学,基于渗透力对岩体的损伤和裂纹起裂的作用以及裂纹扩展导致渗流场改变的原理,建立了渗流-损伤-断裂耦合模型,并对蓄水过程中库岸变形机制进行了分析。王军祥等( 2014) 给出了弹塑性应力-渗流-损伤耦合模型的数值解法,并根据智能反分析方法对不易测定的损伤参数进行了反演。卞康等( 2010) 利用Mazars 各向同性弹性损伤理论和线弹性断裂力学理论,根据水工隧洞衬砌水压致裂的实际过程建立了渗流-损伤-应力耦合模型。李利平等( 2011) 基于压剪和拉剪双重破坏准则,建立了可以适用于煤矿充填体的应力-渗流-损伤耦合方程,并采用有限元对断层活化导致的突水机制进行了研究。翁其能等( 2013) 以代表体积单元( REV) 为研究对象,分析建立了长期处于高水压状态下隧道衬砌的渗流-应力-损伤耦合作用方程。冉小丰等( 2015) 考虑围岩损伤演化特征与渗透性的动态变化特征,建立了渗流-应力-耦合模型,并对某油田钻井过程中泥页岩井壁的稳定性进行了分析。刘黎等( 2016) 建立了采动煤岩体瓦斯渗流-应力-损伤耦合模型,并设计程序对某煤矿瓦斯渗流规律进行了模拟研究。刘仲秋等( 2012) 将围岩和衬砌材料均视为弹塑性损伤材料,对锦屏二级水电站引水隧洞进行了从开挖支护到运行充水全过程的渗流-应力耦合模拟。目前,很多学者试图通过分析岩石细观缺陷结构的演化来解释宏观破裂的发展与耦合过程中现象,把宏观和细观参数通过一定的方式联系起来,成为了当前解决工程问题和取得理论研究突破的焦点。
对于渗流-损伤-应力耦合问题已有的诸多研究,已经取得了一定的成果,但应用弹塑性损伤耦合模型进行巷道变形破坏的分析尚不多见,且现有模型仍需进一步改善以更好地反映岩石物理力学参数的动态变化特征尤其是峰后特征,以及岩体力学特性与水力学特性的不均匀性对岩体破坏的影响。本文基于前人的研究,充分考虑巷道开挖后破坏形态的影响因素,在岩体力学参数及水力学参数符合weibull 分布的假定下,考虑围岩塑性屈服,渗透系数随围岩损伤演化以及围岩力学参数弱化的过程,建立渗流-损伤-应力耦合作用数值模型,并利用多物理场数值模拟软件,模拟分析巷道围岩变形破坏的渐进性过程和关键部位的破坏演化过程,对比分析不同因素作用下巷道围岩变形破坏模式的特征和区别,为合理开展地下工程和矿山工程提供可靠依据和科学指导。
1 渗流-损伤-应力耦合模型的建立
巷道开挖后,围岩将发生应力重分布和应力回弹作用,当围岩无法承受其作用时即发生塑性变形或破坏。前人已对巷道变形破坏类型及影响因素进行了系统地归纳和总结( 谷德振,1979; 张倬元,1981; 于学馥,1983; 王思敬,1984; 何满朝等,2002; 孙广忠,2004; 谢和平等,2015) 。
在应力和渗流的共同作用下,巷道围岩即会处于损伤状态,且损伤随时间发生动态演化,同时损伤反作用于围岩体,使其力学性质和水力学性质发生变化,在应力-损伤-渗流的耦合作用下,巷道围岩产生渐进性的变形破坏。假设岩体介质为多孔弹性介质,下面给出耦合计算模型。
1.1 岩体非均质性的假定
处于地质环境中的岩体,其力学性质在空间上的分布是不均匀的,为了反映巷道围岩的非均质性,引入weibull 统计分布函数来描述岩体的弹性模量、黏聚力、内摩擦角、渗透系数等物理力学参数,即:
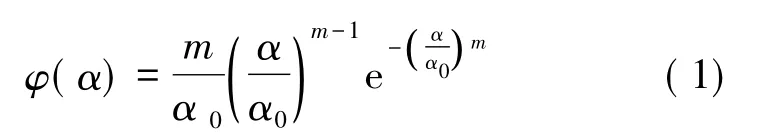
式中,α 为岩体材料参数( 弹性模量等) ; α0为材料参数的均值; m 为均匀性系数; φ( α) 为岩体力学性质α 的统计分布密度。
1.2 岩体力学参数弱化的表述
在应力和渗流环境中的岩体损伤实质上是岩体的力学参数不断降低的过程( 江权,2008) 。地下工程岩体开挖后,由原先的三向应力状态转向两向应力状态,相当于完成了一次复杂的加、卸载过程,在此过程中产生应力重分布作用,应力集中或卸荷作用使得岩体产生不同程度的损伤,并导致一定范围的屈服破坏,随着损伤范围和屈服范围的动态扩大,应力将不断发生重分布,进而又造成了更大范围的损伤和屈服,并形成了损伤和应力重分布相互促进的动态过程。细观上,在渗流、应力作用下围岩内部原有的微小裂隙从闭合状态趋于张开,并产生一定的扩展延伸,同时在拉应力和劈裂作用下围岩可能促使新裂隙产生并发生裂隙间的贯通,使得围岩性质产生明显的劣化,从宏观上可以认为岩体的弹性模量、黏聚力、内摩擦角等力学参数发生了变化( 黄勇等,2018; 赵晶等,2018) 。
从理论分析和现场实际工程经验中,均可得知岩体的弹性模量随着其受损程度的增加,而发生弱化不断减小。根据典型的岩石单轴加载应力-应变曲线( 图1) ,可以得出在弹性阶段岩石的弹性模量基本保持不变或变化很小,进入屈服阶段后,岩石的弹性模量开始下降,且其下降的速度由缓慢逐渐增加,在岩石达到峰值强度时变化速度不断加快,直至岩石达到残余强度时,岩石的弹性模量跌落到残余值并基本不再发生变化。这一过程是加载进行时岩体的弹性模量随着塑性应变的变化而发生的,而等效塑性应变可以用来较好的描述岩体屈服后的塑性程度,即:
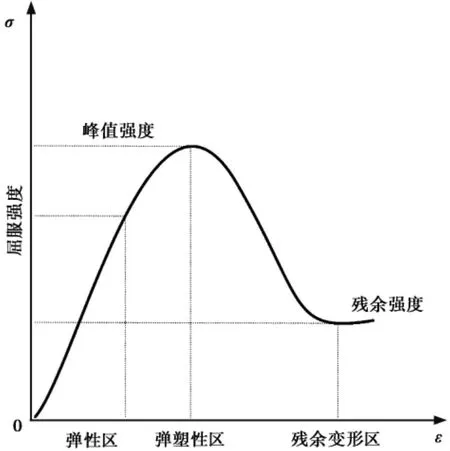
图1 岩石单轴加载应力-应变曲线图Fig. 1 Rock stress-strain curve in uniaxial loading
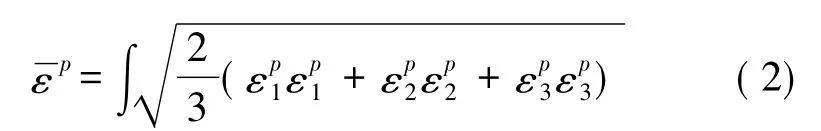
因此,基于典型的岩石应力-应变曲线特征,考虑工程岩体弹性模量在加载过程中动态变化的特点,充分反映岩体力学参数的峰后变化特点以及应力跌落的突然性,简化其弱化的过程如图2,建立弹性模量关于岩体等效塑性应变的二次型弱化函数关系:
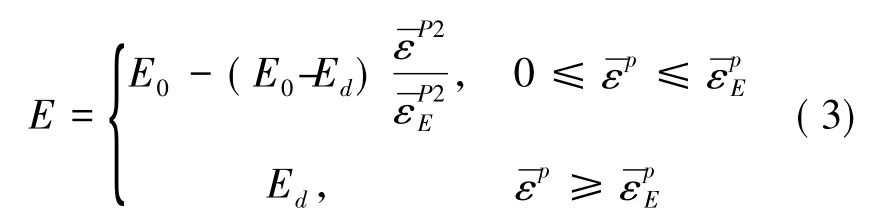
式中,E 为岩体的弹性模量; E0和Ed分别为岩体的初始弹性模量和到达残余阶段时的残余弹性模量;为等效塑性应变;为弹性模量达到残余值时的等效塑性应变。
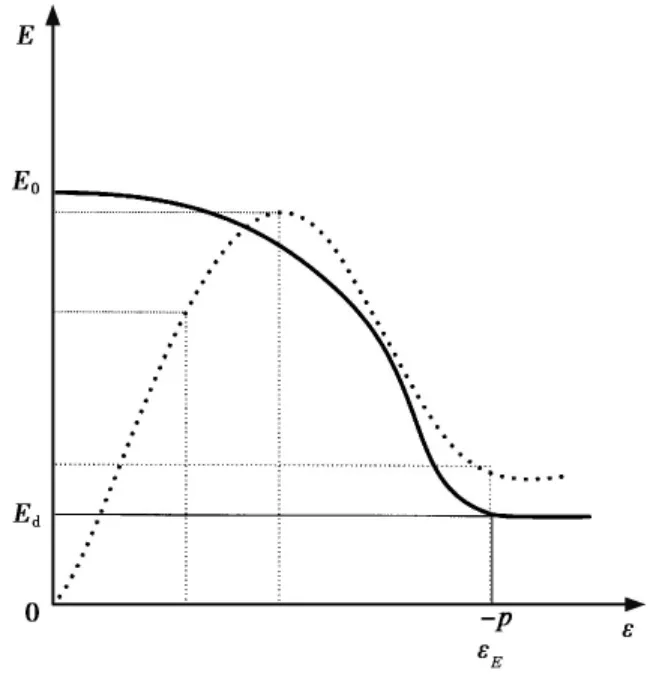
图2 弹性模量弱化过程曲线Fig. 2 Rock modulus of elasticity curve of weakening process
1.3 损伤变量的定义
为了定量描述巷道围岩的损伤程度,定义损伤变量D。考虑到岩体在达到屈服极限时,开始出现明显的损伤现象并产生一定的塑性应变,因此本文将等效塑性应变作为损伤程度的判据,并通过上文弹性模量E 的弱化来定义损伤变量D,建立如下损伤演化方程:
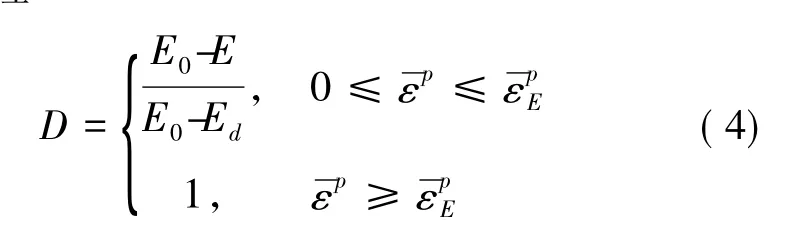
考虑到岩体加卸荷过程中,当发生屈服作用时,微裂隙趋于张开,产生新裂隙并使裂隙间趋于贯通,从细观角度上来看,岩体内部结构不断分离,不连续面增多,岩体的完整性受到了破坏,表现为细观参数黏聚力和内摩擦角的减小。据此建立简化的岩体损伤过程中黏聚力c,内摩擦角φ 的动态损伤变化过程:
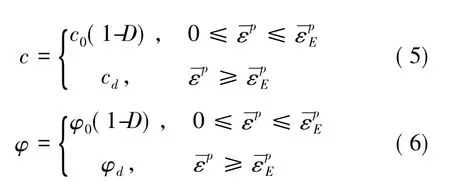
其中,C0和Cd分别为岩体的初始黏聚力和到达残余阶段时的残余黏聚力; φ0和φd分别为岩体的初始内摩擦角和到达残余阶段时的残余内摩擦角。
1.4 应力场控制方程
假定研究对象为理想弹塑性体,考虑流体的孔隙水压力作用和损伤影响的本构关系如下:
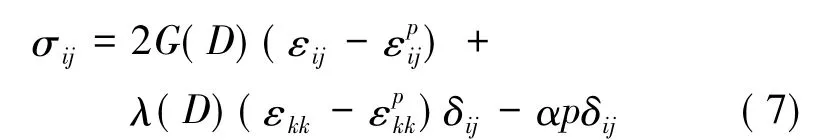
式中,σij为应力分量; G( D) 为岩体的剪切模量,是损伤变量D 的函数; λ( D) 为拉梅常数,其值大小为E( D) ν/[( 1 +ν) ( 1-2ν) ]; E( D) 为岩体的弹性模量,为损伤变量D 的函数; ν 为泊松比( 变化忽略不计) ; εij为应变分量;为塑性应变分量; εkk为体积应变分量;为塑性体积应变分量; δij为Kronecker 系数; α 为Boit 系数; p 为孔隙水压力。

式中弹性部分可根据胡克定律计算求解,塑性部分采用基于D-P 准则的理想弹塑性模型,其屈服条件为:
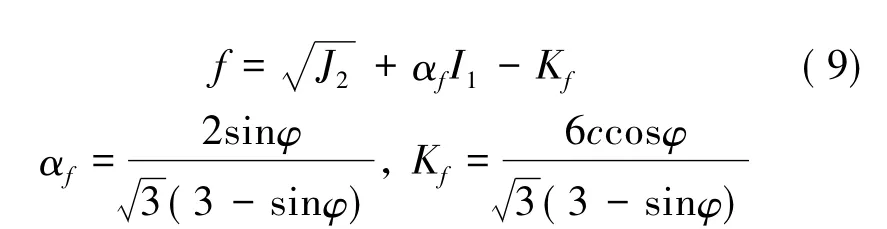
其中,αf、Kf为与岩体内摩擦角φ 和黏聚力c 有关的实验常数; J2为应力偏量第二不变量; I1为应力第一不变量。
1.5 渗流场方程
假设流体不可压缩,无源稳定情况下的渗流连续性方程为:
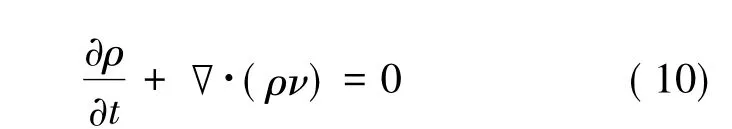
代入Darcy 定律方程,得到渗流场控制方程为:
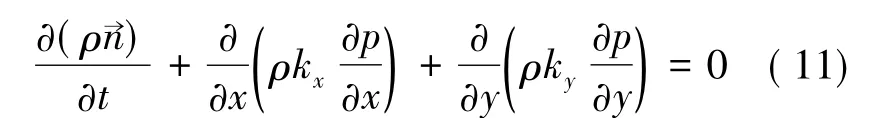
通过室内进行的岩石全应力-应变过程渗透性试验结果可知( 李世平,1995; 韩宝平,2000; 姜振泉,2001;李树刚,2001) ,岩石在所受荷载逐渐增大的过程中,会发生细观结构的损伤,其渗透率在此过程中会发生突跳性增长,因此,为表述这一现象引入渗透率突跳系数( 杨天鸿等,2001) ,同时考虑应力和损伤过程对渗透系数的影响,假定应力与渗透系数呈负指数关系,建立损伤演化过程中的渗流-应力耦合方程如下:
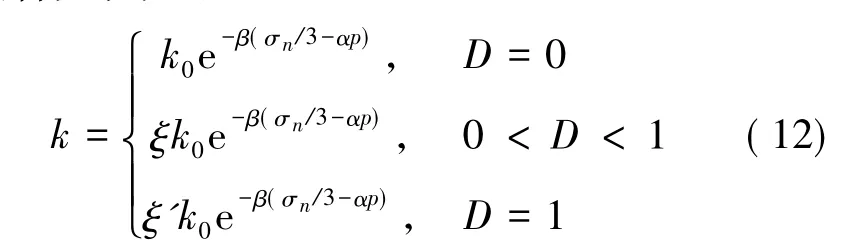
其中,k 和k0分别为渗透系数和渗透系数初值; P 为孔隙水压力; ξ、α、β 分别为渗透系数突跳倍率、孔隙水压力系数、耦合系数。
2 数值模拟结果分析
2.1 数值模型的建立
为了验证耦合模型的合理性,建立巷道平面应变计算模型( 图3) ,计算区域为宽( x 方向) 40 m,高( y 方向) 40 m 的正方形,巷道断面采用半圆拱形,圆半径为3 m,矩形区域宽6 m,高3 m。采用三角形单元网格剖分,共划为6636 个域单元和228 个边界单元。模型底部施加固定约束,初始地应力等效为边界荷载施加于两侧和顶部,孔隙水压力施加于模型顶部,巷道内边界为自由界面且初始水头为零。巷道围岩物理力学参数及耦合参数如表1 所示。

图3 数值模拟的计算网格模型Fig. 3 Calculate grid model of numerical simulation
2.2 力学参数弱化对巷道变形破坏影响分析
为了反映力学参数弱化对巷道围岩损伤破坏情况的影响程度,采用以上计算参数,在相同的初始地应力和边界条件下,分别对不考虑参数弱化和考虑参数弱化的两种情况进行计算。不考虑渗流、应力对岩体损伤的影响,忽略加卸载过程中岩石物理力学参数的动态变化,并认为参数为常值时,计算结果如图4 所示,当考虑力学参数按模型给出的方式弱化时,计算结果如图5 所示。
模型计算结果显示,在考虑力学参数弱化过程的渗流-应力耦合模型计算中,塑性屈服破坏区要明显大于未考虑力学参数弱化时的情况,这主要体现了在加卸载过程中围岩体处于损伤演化的过程,不连续面的延伸、贯通和产生对于岩体整体质量的损伤作用无法忽略,反映出岩体损伤动态变化的过程对于巷道围岩的变形破坏的程度可产生较大的影响,表明了在渗流-应力耦合计算过程中引入力学参数弱化的必要性。
2.3 不同深度下巷道变形破坏分析
地下工程围岩体的变形破坏常常是渐进性发展的,由于岩体的非均质性、几何结构特点、应力分布不均匀等原因,应力集中程度最高的部位往往成为巷道围岩变形破坏的突破口,在局部产生破坏后应力重分布作用将应力转移至其他部位,再次引起其他部位的逐一破坏,最终导致大范围的失稳破坏。长期以来,人们对自重应力引起的变形破坏进行了大量的研究,但随着地下工程的深度不断增加,尤其是受到褶皱和挤压性断层等构造因素影响的区域,水平地应力可能会成为影响巷道稳定性的主导因素。考虑到不同深度地应力下巷道围岩变形破坏过程的差异性,根据侧压力系数的取值,分别设置3 种情形进行计算分析。情形一: 水平地应力等于垂直地应力,侧压力系数λ =1; 情形二: 水平地应力大于垂直地应力,侧压力系数λ = 2; 情形三: 水平地应力小于垂直地应力,侧压力系数λ =1/2。计算组合详细的地应力取值见表2。

表1 数值模拟的计算参数Table 1 Physical and mechanical parameters for numerical simulation
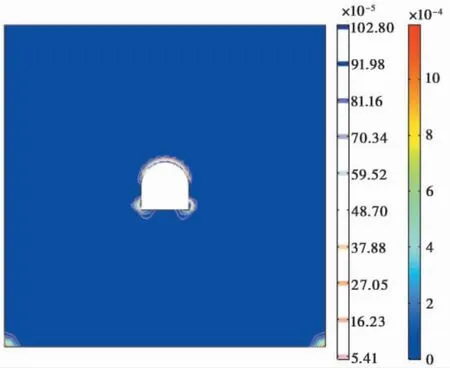
图4 不考虑参数弱化的塑性屈服云图Fig. 4 Plastic yield contours without considering parameter weakening
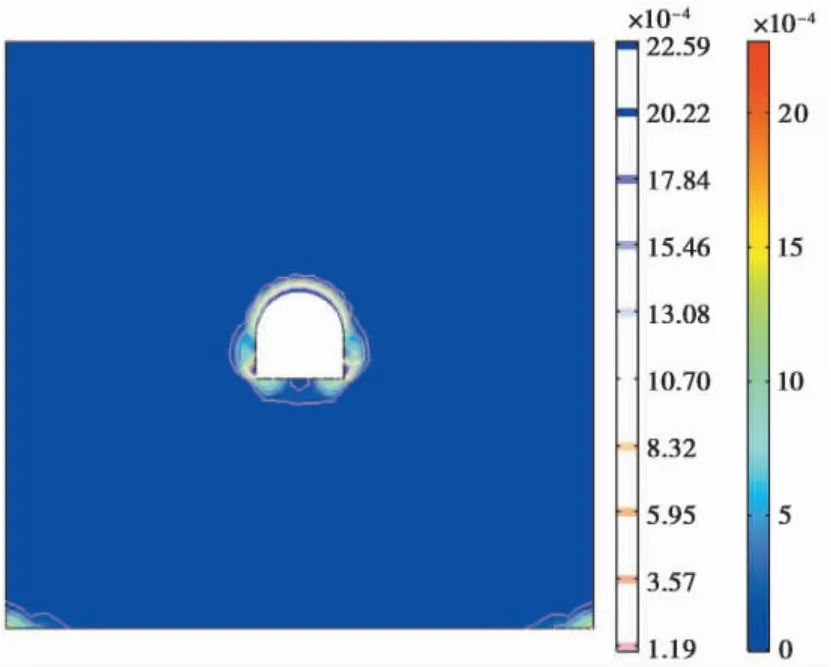
图5 考虑参数弱化塑性屈服云图Fig. 5 Plastic yield contours considering parameter weakening

表2 不同侧压力系数下的地应力Table 2 Initial stress with different lateral pressure coefficients
当侧压力系数等于1时,巷道围岩塑性屈服区的变化过程如图6 所示。从图中可以看出,巷道底角处最先产生屈服破坏,随着时间的推移,顶拱附近开始产生明显的环形损伤屈服区,并逐渐向边墙延伸最后塑性区发展到整个巷道周边,呈现出四周近乎均匀的屈服破坏状态。这表明在水平地应力与垂直地应力趋于相等的情况下,底角处因其棱角状容易形成应力集中区,切向应力过大导致该处首先产生屈服,继而顶板由于在重力作用下所受拉应力相对较大,从顶板开始不断向两侧边墙发生屈服,因为水平和垂直地应力均发挥主导作用,所以巷道围岩最后的状态大致为沿巷道周边形成了近于均匀的屈服状态。
当侧压力系数为2 时,巷道围岩塑性屈服区的变化过程如图7 所示。从图中可以看出,巷道顶拱处最先产生塑性屈服,随着时间的推移,水平应力向深部传递的趋势十分明显,顶拱和底板处产生均出现较大程度的屈服并不断发展扩大,最后在顶拱和地板处形成了不规则梯形状的屈服区。这表明了在这种地应力水平下,水平应力过高导致顶板处产生较大的剪切应力,剪切应力集中使得顶拱处成为应力集中系数最高的部位,因此首先产生屈服破坏,继而底部由于同样承受较大的剪切应力,故屈服破坏主要沿顶拱、底板处延伸发展,而两侧边墙的变化程度很小,可见在水平地应力主导的情况下,顶、底部是最容易发生破坏的部位,顶部容易发生剪切破坏、楔形冒落等现象,底部容易产生底鼓、褶皱体破坏等现象。
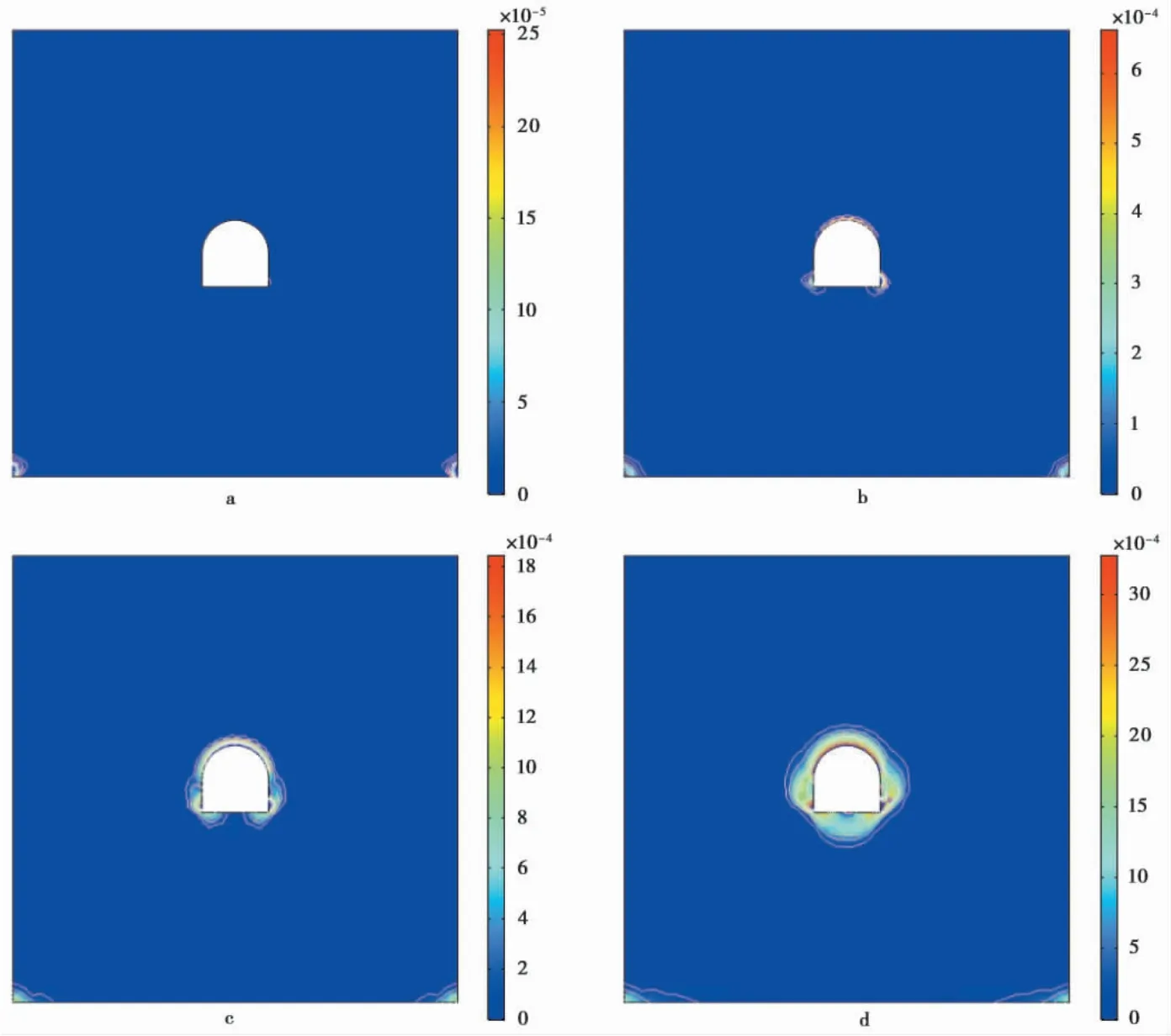
图6 侧压力系数为1 时的破坏过程Fig. 6 Damage process under the lateral pressure coefficients of 1
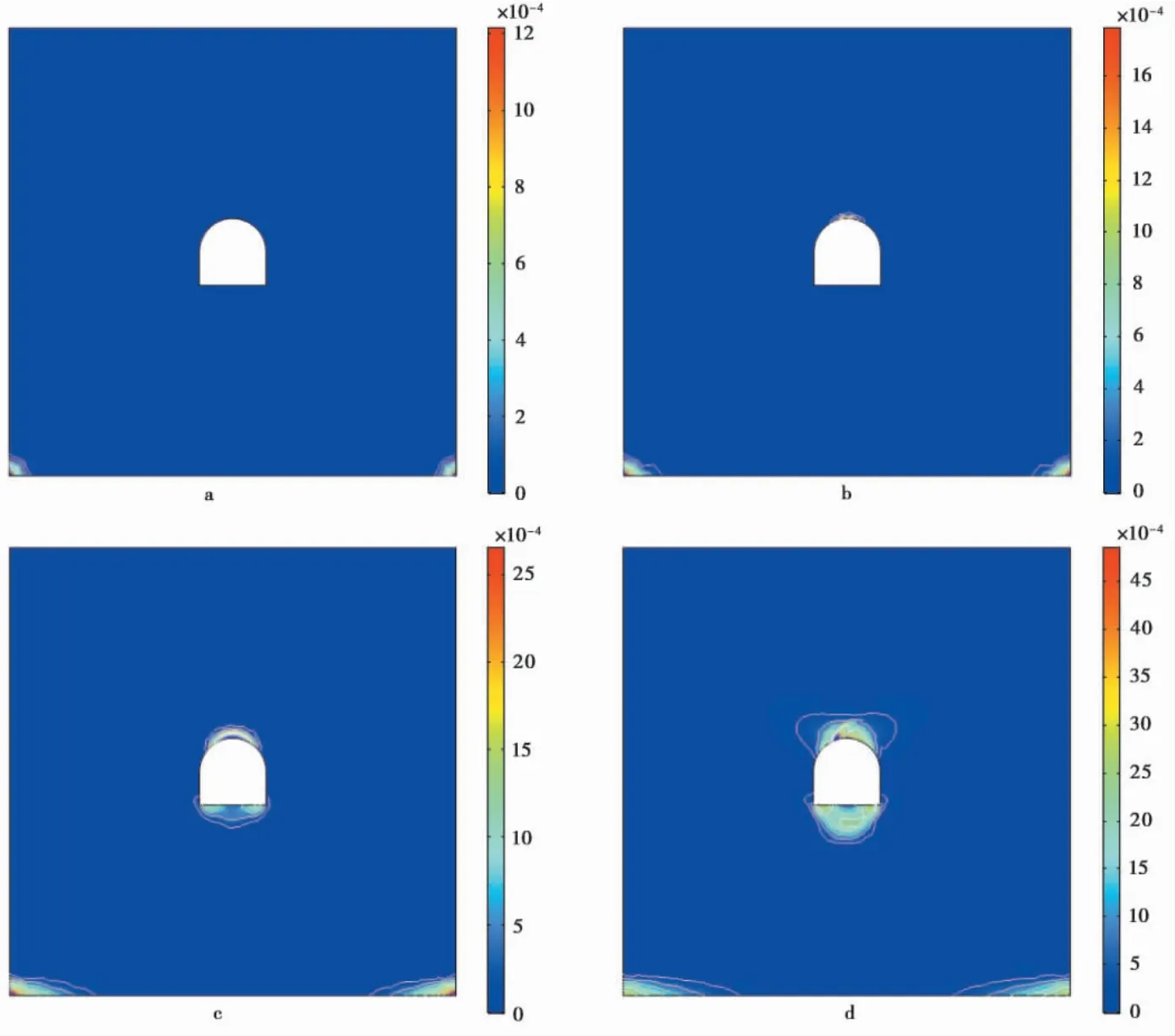
图7 侧压力系数为2 时的破坏过程Fig. 7 Damage process under the lateral pressure coefficients of 2
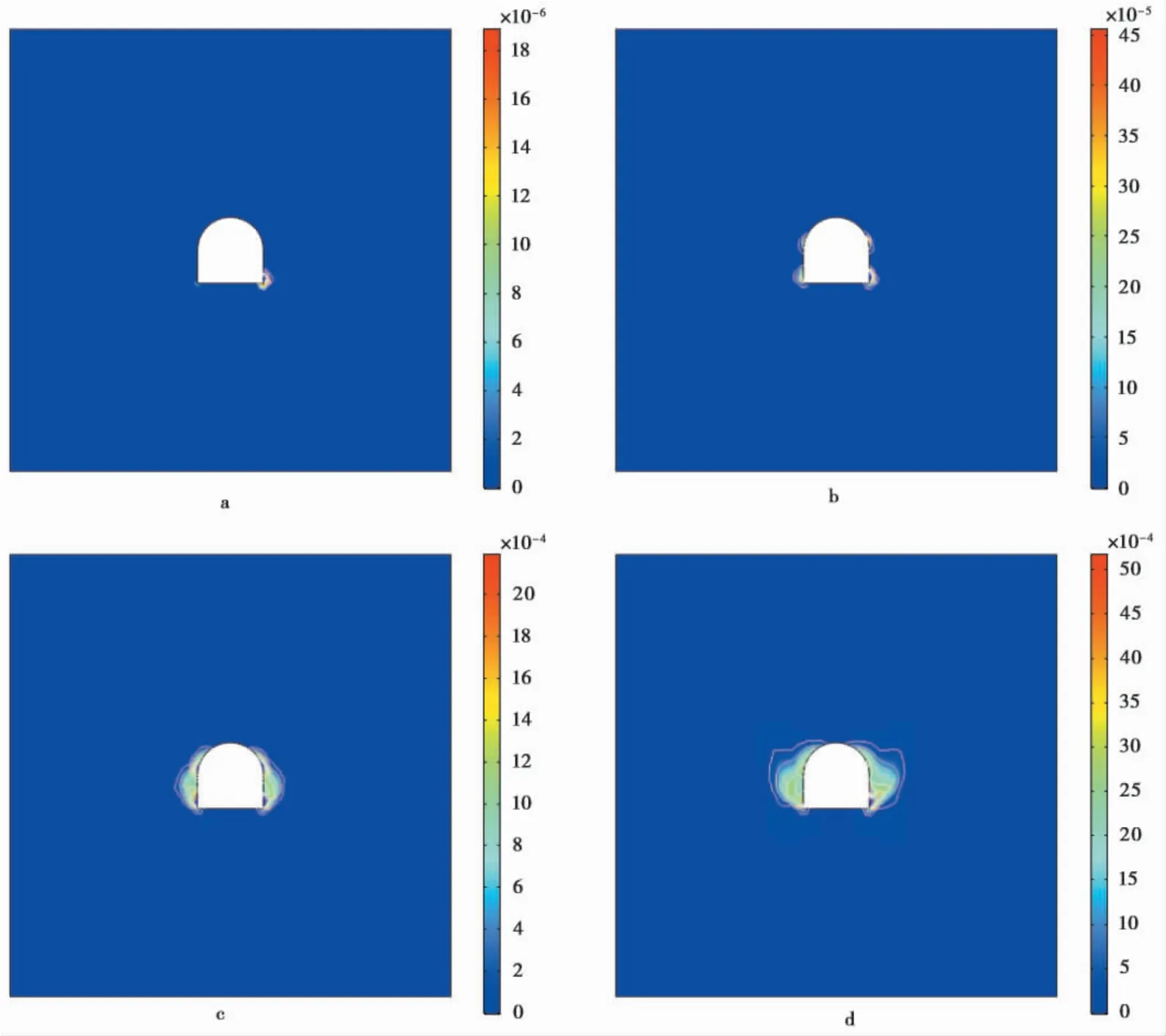
图8 侧压力系数为1/2 时的破坏过程Fig. 8 Damage process under the lateral pressure coefficients of 1/2
当侧压力系数为1/2 时,巷道围岩塑性屈服区的变化过程如图8 所示。从图中可以看出,在巷道底角处因应力集中首先产生屈服之后,巷道两侧的边墙拐角部位也开始产生损伤破坏,并沿两侧边墙不断扩展,最后覆盖整个边墙区域,在两侧边墙处形成了不规则条带状的屈服区,而在顶、底板处变形相对较小。这表明了在垂直地应力占主导作用的情况下,巷道的破坏变形过程有着明显的区别,在围岩两侧更容易产生剪切应力集中,因此两侧边墙是最可能产生破坏的部位,有可能发生表层剥落、脆性错断甚至在顶角处产生大块楔形体坍落、岩爆的现象。
由损伤屈服面积的变化过程曲线( 图9) 可以看出,在地应力水平不同情况下的加载过程,损伤区面积均呈现不断增加的趋势,且变化速度均为不断加快。这表明随着加载过程的进行,岩体损伤破裂的程度不断加剧,耦合作用效果逐渐加强,在多物理场耦合的作用下,岩体的力学参数不断弱化,岩体质量逐渐降低,使岩体产生屈服破坏形成损伤区的速度变得更快。
3 结 论
本文首先总结了前人关于岩体损伤与渗流-应力耦合的研究。在充分考虑了岩体的非均质性、塑性阶段的屈服过程以及岩体力学参数随加卸载状态发生动态弱化的基础上,建立了渗流-损伤-应力耦合的数值计算模型。将建立的渗流-损伤-应力耦合模型应用于巷道围岩变形破坏的模拟,主要结论如下:
(1) 考虑力学参数弱化的耦合模型与其他模型相比,得出了更加严重的围岩变形破坏结果,充分反映了巷道开挖后应力重分布对于围岩造成的不可逆转的损伤作用,损伤必然造成力学参数的弱化,这种损伤是必然存在且不可忽视的,每一时步动态损伤所造成的结果必然会对下一时步的加卸载过程造成影响,产生叠加损伤效应,这将对巷道围岩的稳定性产生更加不利的影响,而这在以往的模型中并没有充分体现。由于材料损伤对于工程问题的重要性,应从损伤状态变化的角度上考虑渗流-损伤-应力耦合问题,才能提出更能保证安全和符合实际的解答。
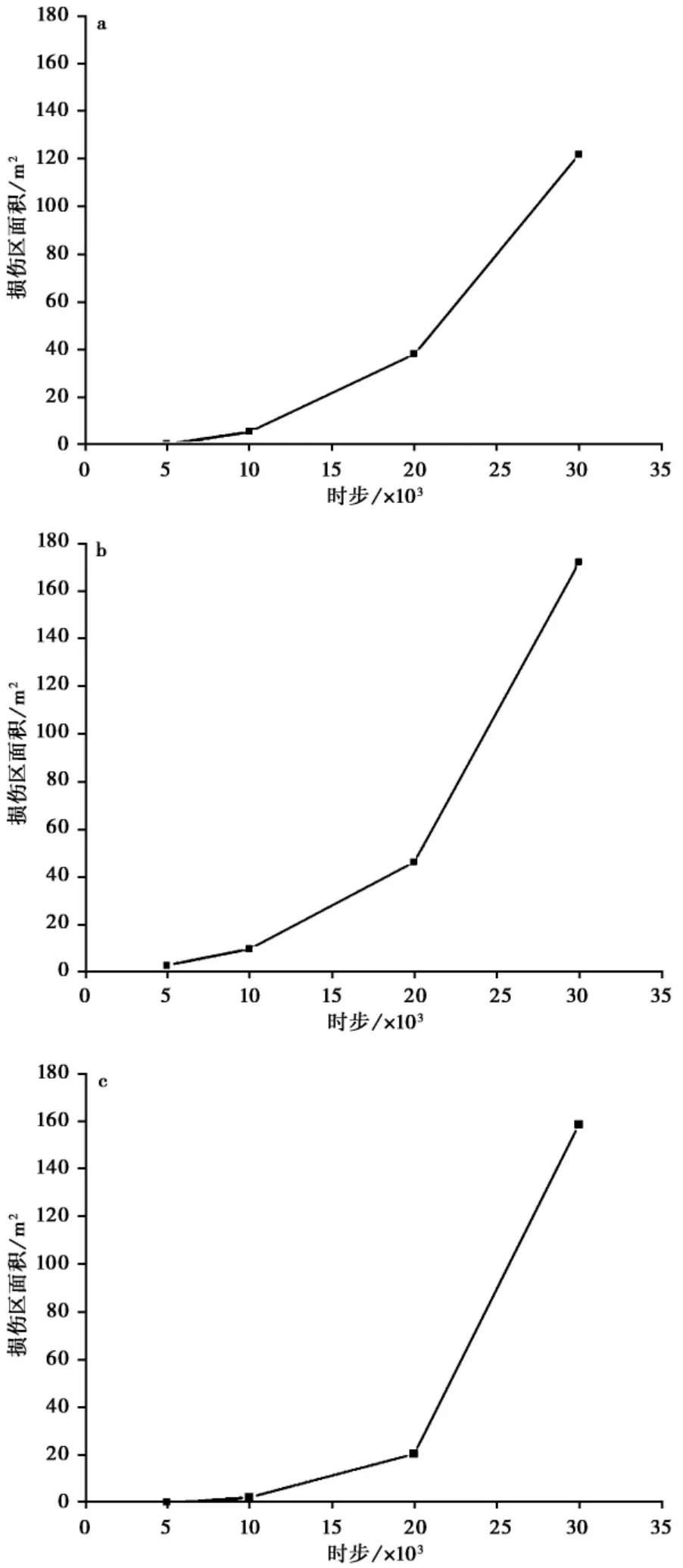
图9 侧压力系数为1、2、1/2 时损伤面积的变化过程Fig. 9 Change of damage area under the lateral pressure coefficients of 1、2、1/2
(2) 应用本文提出的模型对处于不同深度和地应力水平下的半圆拱形巷道稳定性进行分析,通过其屈服破坏的渐进过程,得出在渗流-损伤-应力耦合作用下,产生破坏失稳的过程是由缓慢到逐渐加快的,多物理场耦合作用的效果是逐渐加强的,当侧压力系数趋向于1 时,巷道周边最终均会发生相近程度的屈服破坏,当侧压力系数大于1 时,巷道顶拱和地板最终会出现似梯形状的大面积破坏,当侧压力系数小于1 时,屈服破坏区则主要分布在巷道两侧边墙处,呈不规则条带状。结论对于地下工程进行开挖后,能正确掌握并控制不同地应力下巷道发生破坏的关键部位,并有针对性地采取经济合理的支护措施来加固围岩有着重要意义。
