非API规格套管在弯曲井段可下入性的计算

李建亮，王 磊，姬丙寅，史交齐

（1.衡阳华菱钢管有限公司，湖南 衡阳 421001；2.中石化西北油田分公司物资供应管理中心，新疆 轮台 841600；3.西安三维应力工程技术有限公司，陕西 西安 710075）

套管在弯曲井眼里的可下入计算，是在下套管作业前判断在弯曲井眼能否顺利下入套管的重要计算依据。文献［1-3］推荐了一些套管可下入性的计算方法，同时根据已有的相关经验，在钻井设计初期选择狗腿度及套管时就有考虑。而对于非API规格套管可下入性分析报道较少，为保证下套管作业的安全施工，提高钻井的经济效益，研究非API规格套管可下入性计算十分必要。目前，计算方法主要有解析法和有限元法［4］，采用以上方法对非API规格套管下入性进行计算分析，以期为非API规格套管下入提供理论支持。

1 套管可下入性解析计算分析

1.1 套管不产生变形通过井眼的长度计算分析

井眼曲率半径与狗腿度的关系为：

式中R——井眼曲率半径，mm；

L——测量的长度，mm；

φ——狗腿度，°/25 m。

套管不产生变形［1］通过井眼的几何模型如图1所示。

由图1的几何关系可推导出公式（2）：

图1 套管不产生变形通过井眼的几何模型示意

式中ds——接箍外径，mm；

d——套管外径，mm；

D——井眼直径，mm；

L1——套管不产生变形通过井眼的长度，m。

由公式（2）可得出套管不产生变形通过井眼的长度L1与井眼直径、套管外径、接箍直径及井眼曲率半径的关系，公式如下：

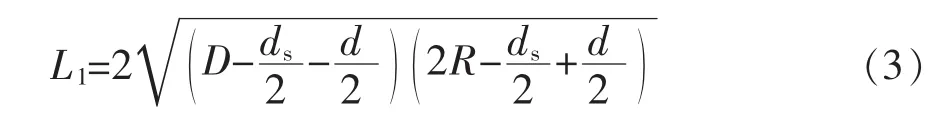
1.2 套管产生变形通过井眼的计算分析

由以上分析可知，对于特定的井眼和套管，如果狗腿度较小，套管不需要发生变形就能通过，然而狗腿度较大的井段套管需要产生变形才能通过井眼。套管产生变形通过井眼的几何模型如图2所示。

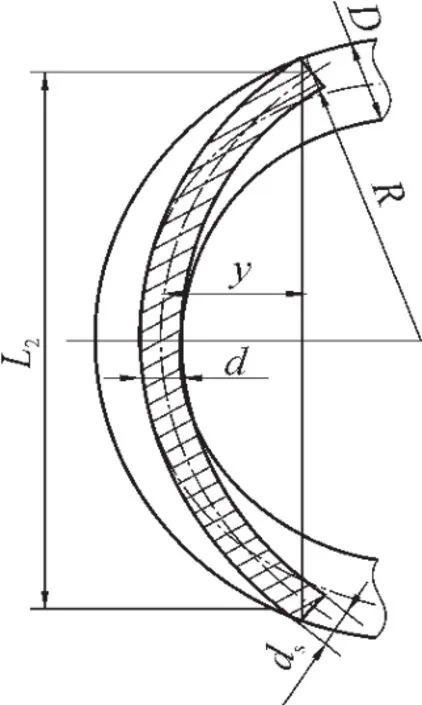
图2 套管产生变形通过井眼的几何模型示意

由图2可得出公式（4）：

式中y——通过井眼需要的挠度，mm；

L2——套管产生变形通过井眼的长度，m。

1.3 套管通过弯曲井眼受力分析

在弯曲井眼中，套管在下入过程中，还受轴向力和侧向力的作用，根据材料力学纵横弯曲概念，如果杆件的刚度很大，弯曲变形很小，可以忽略轴向力对弯曲变形的影响。此处套管的刚度均较大，忽略轴向载荷，建立套管受集中载荷的简支梁力学模型，套管柱弯曲简支梁力学模型如图3所示。由公式（5）～（6）计算的挠度反推轴向载荷和集中载荷。

图3 套管柱弯曲简支梁力学模型

式中E——弹性模量，MPa；

I——转动惯量，kg·m2；

P——轴向载荷，kN；

Q——集中荷载，kN。

2 非API规格套管可下入性算例

以Φ478.56 mm×21.00 mm规格P110套管通过Φ558.80 mm井眼为例计算说明。

2.1 套管不产生变形通过井眼的长度计算

井眼直径D=558.8 mm，接箍外径ds=508.00 mm，套管外径d=478.56 mm，由公式（1）和公式（3）可得出狗腿度φ与套管不产生变形能够通过井眼的长度L1的关系如图4所示。

图4 狗腿度和套管柱不产生变形能够通过井眼的长度的关系

由图4可知：当狗腿度小于约1.2°/25 m，25 m的Φ478.56 mm套管不需要发生弯曲变形就能够通过Φ558.80 mm井眼；当狗腿度大于约1.2°/25 m，需要产生弯曲变形。

2.2 套管产生变形通过井眼的计算分析

D=558.8 mm，ds=508.00 mm，d=478.56 mm，L2=25 m，由公式（4）可得出狗腿度φ和套管柱能够通过井眼需要的挠度关系如图5所示。

图5 狗腿度和套管柱能够通过井眼需要的挠度的关系

由图5可知：当狗腿度≤1.2°/25 m，25 m的Φ478.56 mm套管柱需要的挠度为0，通过Φ558.80 mm井眼；当狗腿度∧1.2°/25 m，需要的挠度随着狗腿度的增加而逐渐增加，并呈线性变化。

2.3 套管通过弯曲井眼受力分析

D=558.8 mm，ds=508.00 mm，d=478.56 mm，L2=25 m，由公式（4）可得出狗腿度φ和套管柱能够通过井眼需要的轴向载荷的关系，以及狗腿度和套管柱能够通过井眼产生的弯曲应力的关系，如图6~7所示。

图6 狗腿度和套管柱能够通过井眼需要的轴向载荷的关系

由图6~7可知：套管柱能够通过井眼需要的轴向载荷与狗腿度呈非线性增加，狗腿度为2°/25 m时需要的轴向力为70 kN，狗腿度为10°/25 m时需要的轴向力为160 kN。弯曲应力与狗腿度呈线性变化，当狗腿度为2°/25 m，弯曲应力为71 MPa，应力水平较低，当狗腿度为10°/25 m，弯曲应力为 515 MPa。因此，当狗腿度为2°/25 m，Ф478.56 mm×21 mm套管柱在Ф558.80 mm井眼中能够安全通过。

图7 狗腿度和套管柱能够通过井眼产生的弯曲应力的关系

3 套管可下入性有限元分析

3.1 计算模型

d=478.56 mm，壁厚 t=21.00 mm，E=2.1×105MPa，材料屈服强度σs=758 MPa，材料泊松比μ=0.3。对于地层，材料弹性模量E=25 000 MPa，材料泊松比μ=0.3，地层与套管摩擦因数f=0.5。建立地层和套管模型，由于结构的对称性，取模型的1/2进行分析，并假设套管和地层初始接触位置如图8所示。套管顶端节点施加X、Y方向约束，套管顶面节点施加竖直向下的位移。模拟套管在2°/25 m，10°/25 m井眼中的通过能力。建立井眼模型，井眼的垂深为25 m，套管取35 m长。

图8 10°/25 m井眼和套管模型

3.2 计算结果

当井眼狗腿度为2°/25 m，套管下深25 m需要的最大轴向载荷为21.3 kN，随着下深位置的变化，在两种井眼中下套管需要的轴向力变化如图9所示，在全井任何位置套管柱都能提供此轴向载荷；套管最大等效应力为123 MPa，随着下深位置的变化在两种井眼中套管等效应力变化如图10所示，Ф478.56 mm×21 mm套管柱最大质量约为325 t，对套管产生的轴向应力约为130 MPa，与井眼的弯曲效应引起的套管的等效应力组合，套管最大应力约为250 MPa，和屈服强度758 MPa相比，仍有3.0左右的安全系数。因此，当狗腿度为2°/25 m，Ф478.56 mm×21 mm套管柱在Ф558.80 mm井眼中能够安全通过。

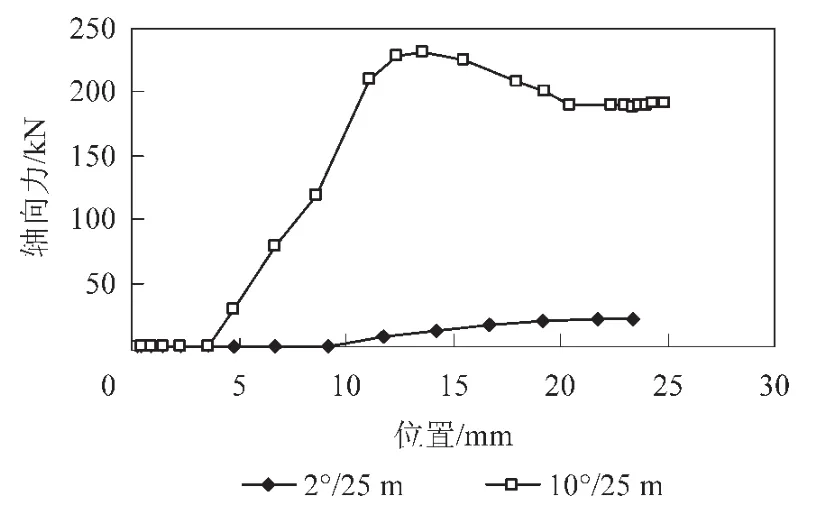
图9 两种井眼中下深位置与下套管需要的轴向力的变化关系

图10 两种井眼中下深位置与套管等效应力的关系

当井眼狗腿度为10°/25 m，套管下深25 m需要的最大轴向载荷为215 kN，2°/25 m井眼下深为25 m时等效应力云图如图11所示，在距井口120 m内，套管柱不足以提供轴向载荷，在此段内套管不能下入；另外，套管最大等效应力为622 MPa，10°/25 m井眼下深为25 m时等效应力云图如图12所示，仅井眼弯曲效应引起的等效应力非常大，Ф478.56 mm×21 mm套管柱最大质量约为325 t，对套管产生的轴向应力约为130 MPa，与井眼的弯曲效应引起的套管的等效应力组合，套管最大应力约为750 MPa，几乎等于套管屈服强度758 MPa。因此，当狗腿度为10°/25 m，Ф478.56 mm×21 mm套管柱在Ф558.80 mm井眼中是不能够安全下入的。

图11 2°/25 m井眼下深为25 m时等效应力云图

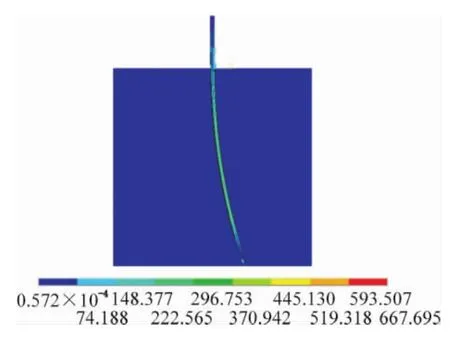
图12 10°/25 m井眼下深为25 m时等效应力云图

为了计算方便，在建立模型时忽略了套管接头的影响，实际情况由于接箍外径大，会增加管柱的刚度；因此需要提供的轴向载荷会略高，另外套管下入时接箍端面与井壁的接触也会增加下入载荷。

4 结 语

（1）采用解析法和有限元法对非API规格套管柱在弯曲井段的可下入性进行分析计算，计算结果表明解析法和有限元法结果基本一致。

（2）解析计算公式能够满足现场运用，为非API规格套管下入提供理论支持。