运用非线性Mohr-Coulomb破坏准则分析尾矿坝稳定性

杜 镀，张向阳，王肖辉，刘智振

(1.河南建筑职业技术学院，郑州 450064；2. 中南大学 资源与安全工程学院，长沙 410083)

尾矿库是专门用来存放废弃矿渣的场所，是矿山的必须生产设施，同时也是人造泥石流的高危险源[1-2]。在尾矿坝的修建过程中，由于存在设计不合理、要求不达标、超负荷使用、地震、强降水等人为或自然灾害因素，造成尾矿坝在服务期内出现溃坝、漏坝等事故。一旦发生尾矿库溃坝、漏坝事故，将会对周边及下游的居民造成生命安全威胁，造成巨大的经济损失，以及造成严重的环境问题[3-4]。

对尾矿库事故问题的研究，美国Clark University公害评定小组通过对全球90余种公害、事故隐患进行了系统的研究分析，结果表明，尾矿库事故位列第18位，其危害仅次于核辐射、核爆炸等危害[5-6]。我国尾矿库事故发生频率高，通过对我国20世纪60年代以来发生的30起尾矿库事故原因进行分析，结果表明仅溃坝事故一项就占到尾矿坝事故总数的一半，溃坝事故的根本原因是坝体稳定性造成的，因此对尾矿坝的失稳问题的研究必须受到高度重视。

目前对尾矿坝的稳定性分析研究，通常将其视为复杂的边坡问题来处理，采用土力学的传统理论进行分析研究[7]。在众多关于边坡稳定性的分析方法中，被广大研究人员认可的主要有极限平衡法[8]、数值分析法以及极限分析法[7-9]等。极限平衡法[10]主要是利用刚体极限平衡理论的条分法，主要有Bishop法、Mogenstern-Price法、Janbu法、Fellenius法等。数值分析法主要有有限元法[9]、有限差分法以及离散元法[11]等。与极限平衡法相比，极限分析法则更严密，解决问题过程更简便，是分析尾矿坝稳定性更有效的方法。极限平衡法[8,12]是一种传统的近似求解土力学稳定问题的方法，但其基本上不考虑岩土体的运动学条件[13]，而极限分析理论能在流动法则下考虑岩土的应力—应变关系[14]，且不必对弹塑性的整个过程进行分析，只需要按一定的规则就能推导出临界安全系数。因此，使用极限分析法对尾矿坝的稳定性分析是一个更优的选择。

本文第一部分介绍了非线性Mohr-Coulomb(M-C)破坏准则和切线法的基本理论，采用图示法给出了正应力、内摩擦角和非线性系数与切应力之间的关系。第二部分给出了尾矿坝的破坏模式，并运用上限理论推导了基于尾矿坝对数螺旋破坏模式的安全系数模型，同时将非线性M-C破坏准则引入该模型，得到了尾矿坝上限非线性安全系数模型。第三部分以某尾矿坝为工程背景，分析了抗拉强度和非线性系数对安全系数的影响，同时得到了该尾矿坝的安全系数。

1 非线性M-C破坏准则

非线性M-C强度准则是用来描述岩石破坏时屈服面上最大主应力和最小主应力的非线性关系的准则，该准则可表示为：

(1)

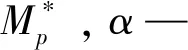
在应力空间中式(1)的等价式为：

(2)

式中：τ、σn—屈服面上的剪应力和正应力；c0—初始黏聚力；σt—轴向拉应力；m—不小于1的非线性系数。

式(2)绘制成曲线见图1。

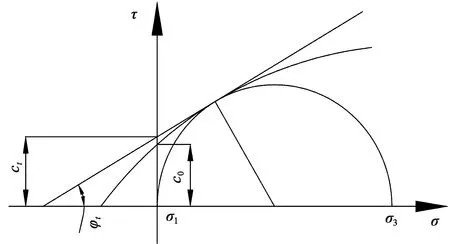
图1 非线性破坏准则与切线法Fig.1 The nonlinear failure criterion and tangent method

图中M点的切线方程为：

τ=ct+tanφt·σn

(3)

式中：φt—切线与σn轴的夹角；ct—切线在τ轴上的截距。

其中：

(4)

由(4)式得：

(5)

将(5)式代入(2)式得：

(6)

将(5)、(6)两式代入(3)式可得ct：

(7)

式(7)即为几个非线性参数的关系式。

当(2)式中c0和σt为常数，σn和m为变量时，可将(2)式绘制成如图2所示的曲线图，直观地解释了σn和m的影响作用。当(6)式中c0和σt为常数，φt和m为变量时，可将(6)式绘制成如图3所示的曲线图，直观地解释了φt和m的影响作用。

2 尾矿坝破坏形式

尾矿坝的形成包括初期的碎石坝和后期的堆积坝，所以尾矿坝是比较复杂的具有一定高度的边坡。为了方便计算和分析，现将尾矿坝进行简化为一般的边坡问题，根据文献[15]中有关边坡的破裂形式，本文将尾矿坝的破坏形式假设为不连续的对数螺线形破裂面。

研究表明，在众多实际中边坡的滑移方式为对数螺线曲面的形式，所以将尾矿坝稳定性问题视为边坡的对数螺线曲面滑移形式计算分析是合理的。假设尾矿坝的破裂滑移面为对数螺线曲面，破坏机构如图4。

图2 σn和m的影响作用Fig.2 Influence of the variation of both σn and m

图3 φt和m的影响作用Fig.3 Influence of the variation of both φt and m

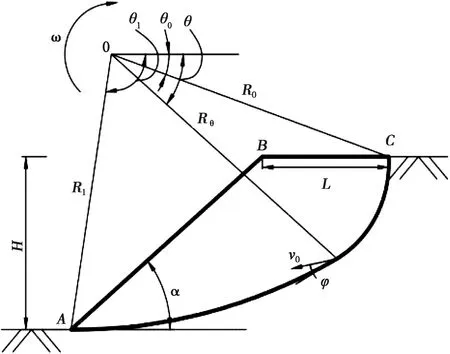
图4 尾矿坝破坏形式Fig.4 Failure mode of tailings dam

对数螺线方程为：

Rθ=R0e(θ-θ0)tanφ

(8)

R1=R0e(θ1-θ0)tanφ

(9)

H=R1sinθ1-R0sinθ0=R0A

(10)

式中：A=(sinθ1e(θ1-θ0)tanφ-sinθ0)

L=R0cosθ0-Hcotα-R0e(θ1-θ0)tanφcosθ1

(11)

根据几何关系可知：

(12)

(13)

式中：B=sinθ1cotα+cosθ1

从式(12)和(13)可知，当θ1、θ0及H确定，R0和L就可完全确定下来，此时旋转中心O就被确定。所以，尾矿坝边坡的破裂滑移面可通过θ1、θ0及H完全确定。

分别求出OAC、OAB、OBC块体重力做的功率WOAC、WOAB、WOBC为：

(14)

(15)

(16)

式中：ω表示旋转角速度

(17)

式中：C=3tanφcosθ1+sinθ1

(18)

(19)

通过WOAC-WOAB-WOBC即可得到块体ABC所做的重力功率Wext为：

(20)

式中：f=f1-f2-f3

将速度间断面AC两侧的块体设为刚体，则内能耗损只发生在速度间断面AC上，AC间断面上的内能耗损率Wint为：

(21)

对任何机动容许的速度场，如果土体重力的功率与速度间断线上内能耗散功率相等，此时尾矿坝对应高度即为尾矿坝的临界高度。

当重力功率与内能耗散相等时，即由Wext=Wint可得：

(22)

将式(7)中ct代替式(22)中c可得：

(23)

H=H(θ1,θ0,tanφt)

(24)

(25)

将安全系数NS代入式(25)中得：

(26)

得安全系数的表达式为：

(27)

3 工程实例

设某尾矿坝的土体服从非线性破坏准则，坝体材料取c0为90 kPa，σt为247.3 kPa，γ为20 kN/m3，φ为18°。基于M-C非线性破坏准则，研究抗拉强度σt和m系数对尾矿坝安全系数NS的影响时，参考文献[16]中m的取值，将m取值1.1～2.0；σt取值250～300 kPa。求解结果见图5。

图5表明，在非线性破坏准则下，尾矿坝安全系数NS随着非线性系数m和抗拉强度σt的增大均减小。

将尾矿坝参数H、c0、σt、γ、φ、代入式(27)，m取1.1即可求得该坝的安全系数。根据式(27)和坝体相关参数求解得到该尾矿坝安全系数为5.54。此安全系数仅在假设m取1.1时将其他尾矿坝参数代入式(27)求得。而根据图5，当安全系数为5.54时，对应了多组不同的σt值和m系数。所以图5可以作为设计参考图调整设计参数，取得更优的设计方案。

图5 σt和m对安全系数NS的影响：(a) NS随σt的变化趋势; (b) NS随m的变化趋势Fig.5 Effects of σt and m on the safety factor NS：(a) The tendency of NS with σt; (b) The tendency of NS with m

4 结论

1)采用切线法将非线性M-C破坏准则运用到极限分析上限法中，基于尾矿坝对数螺线形破坏形式，根据虚功率原理推导了尾矿坝高度的表达式，并且得到了尾矿坝坝体安全系数。

2)将对数螺线形破坏形式引入尾矿坝稳定性分析中，根据工程实例分析计算，结果表明在非线性M-C破坏准则下，随着非线性系数和抗拉强度的增大，尾矿坝的稳定性系数Ns呈递减趋势。

3)通过已知参数计算得到的安全系数NS反算实际设计参数并进行合理调整，可取得更优的设计方案。