临桂新区太平河弯曲河段渡槽槽墩水流特性数值模拟分析

贾 旭

（湖南省建工集团有限公司，湖南 长沙 410000）

0 前言

根据临桂新区工程设计，按照防洪标准，太平河河道需满足100年一遇洪水标准，原太平河河道宽度将由20 m增加至不小于40 m。同时，为减少新修河道占用周边农田，并与周边环境相协调，新设计河道岸线在下游处曲率逐渐变大，与渡槽走向斜交。同时，原渡槽下方，当地村民依墩建有通行简易板桥需同时进行拆除，为不影响后续行人通行，设计方案中确定将渡槽与桥梁同时改建，故而，太平河渡槽改建包含渡槽及人行桥两部分内容。重建渡槽位于新设计河道弯段，设计时仅考虑槽墩与渡槽中心线垂直，未考虑河道内水流方向，为确定槽墩与水流是否顺直，本文针对河道水流流场进行模拟分析。

1 渡槽现状

太平河位于桂林市临桂新区境内，太平河渡槽位于河道中部，原渡槽跨度与老河道宽度基本相同，长度约20 m，渡槽为简支梁式，共3跨，4个槽墩，河道中间槽墩为单矩形柱式，采用浆砌石砌筑，槽身宽度约0.6 m，原渡槽使用年限较久，槽身及槽墩结构已有多处漏水、脱落，加之跨度不满足新河道宽度，故新渡槽改建方案确定将老渡槽进行拆除，并在原址处修建新渡槽。

2 渡槽优化方案分析

2.1 原设计方案水流特性分析

照前述渡槽改建内容，设计单位结合太平河河道设计岸线确定了渡槽设计初步方案，新建渡槽设计过水流量与原渡槽相同，同样采用简支梁式渡槽，每跨9.6 m，设4个槽墩及两个边墩，槽墩由槽身及人行桥共用，两者并列平行布置。渡槽外空尺寸为0.9 m×1.1 m（宽×高），人行桥桥面宽2.3 m，河道内槽墩为适应水流采用圆端形墙状墩身，槽墩尺寸为4.4 m×0.6 m。

槽墩原设计初衷是为适应水流要求，尽可能减少槽墩对水流影响，降低水流对槽墩的冲击，提高槽墩的稳定性。然而，由于渡槽需要在原址上重建，该部位位于新设计河道弯段，设计时仅考虑槽墩与渡槽中心线垂直，未考虑河道内水流方向，为确定槽墩与水流是否顺直，需先对河道水流流场进行模拟。本文选用程凯等二维模型的计算与实测数据对比结果[1]，采用二维模型平面模型对弯曲复式河道进行模拟计算。

根据初步设计水文分析资料，太平河河道入口20年一遇洪水流量为121 m3/s，按照河道断面形式计算入口处平均流速0.67 m/s,同时算得河道水力半径为2.67 m。

基于Wilson等利用激光多谱勒测速仪（LDV）测量室内动床河湾模型中的二次环流[2]，并将测量结果与标准k-ξ双方程模型计算结果比较。表明在采用合理网格布置和差分格式的前提下，标准k-ξ紊流模型能够较好地预测弯曲河道中的主流和二次流流速。

直角坐标系下，标准k-ξ模型的湍动能及其比耗散率输运方程为：

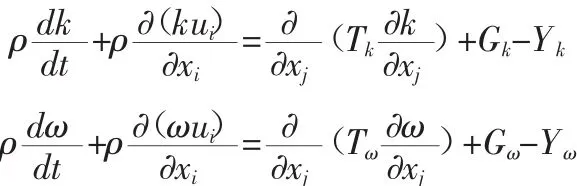
式中：Gk为由层流速度梯度产生的湍流动能；Gω为由ω方程产生的湍流动能；Tk和Tω为k和ω的扩散率；Yk和Yω为由扩散而产生的湍流。

FLuent软件中提供了除标准k-ξ模型外的其他两种k-ξ模型，包括RNG模型以及Realizable模型，针对雷诺数较高的情况（Re＞105），结合标准壁面函数，采用Realizable k-ξ模型，数值计算精度较高。

通过设置监测点获得无槽墩情况下槽墩上游面中心所在位置处流速及速度方向，监测点由左岸至右岸分别为P_1、P_2、P_3、P_4。数值计算后速度场及监测点流速及速度方向统计，见图 1、表 1。

图1 河道流场图

表1 监测点数据统计表

根据以上数值模拟结果，在弯段修建渡槽，采用圆端形槽墩，墩柱轴线与流速方向存在一定角度，对水流条件影响较大。

2.2 渡槽优化设计方案

为缓解上述问题，工程提出新的渡槽设计，即采用对不均匀流场适应性较强的单圆柱形槽墩，槽墩直径为0.8 m。

新建渡槽设计过水流量与原渡槽相同，同样采用简支梁式渡槽，每跨9.6 m，设4个槽墩及两个边墩，槽墩由槽身及人行桥共用，两者并列平行布置。渡槽外空尺寸为0.9 m×1.1 m（宽×高），人行桥桥面宽2.3 m，河道内槽墩为适应水流采用圆端形墙状墩身，槽墩尺寸为4.4 m×0.6 m。

3 槽墩绕流数值模拟

3.1 计算模型

为评价新方案单圆柱形槽墩与原设计方案对水流的影响，本文采用与河道流场分析相同的Fluent软件进行数值模拟。

3.2 模型建立

根据李彬，孙东坡等研究[3]，桥梁与水流斜交且桥墩为圆端形时，桥墩阻水宽度计算采用下式：

式中：B为桥墩阻水宽度，L为桥轴线法线方向的桥墩宽度，b为桥轴线方向的桥墩宽度，α为桥墩长轴轴线与水流方向间夹角。

计算结果见表2。

表2 槽墩特征长度

分别建立同条件下各种槽墩的入流模型，各槽墩尺寸不变，圆端形槽墩与水流方向角度取前述确定角度，计算区域以槽墩直径和阻水宽度中的大值D为特征长度，计算域的长宽分别为30D和20D，槽墩中心距上游及下游面分别为10D和20D，距离左右侧均为10D。

3.3 边界条件及求解设置

数值模拟时，边界条件选用速度入流和自由出流；流场的上下边界采用对称边界条件，以减少边界对水流的影响；槽墩设定为无滑移壁面条件，入流速度及与槽墩的夹角均采用前述计算结果。

求解器为基于压力的分离式求解器，采用二阶隐式时间格式的非定常流动进行计算，压力与速度的耦合计算采用PISO算法，压力的离散为二阶精度离散，动量方程采用二阶迎风格式，计算中压力、密度、体积和动量项的欠松弛因子分别为0.7、1、1、0.7。

3.4 阻力系数

阻力是流体对槽墩的沿流动方向的压力，即为槽墩对水流的阻滞作用力。根据阻力系数公式，计算槽墩阻力系数，见下式：

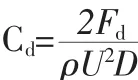
式中：Fd为流体作用于单位长度柱体上沿顺流方向的分力。

结果见表3。

表3 各类型槽墩阻力系数

经过数值模拟后的速度流线见图2～图6。

图2 1#槽墩速度矢量图

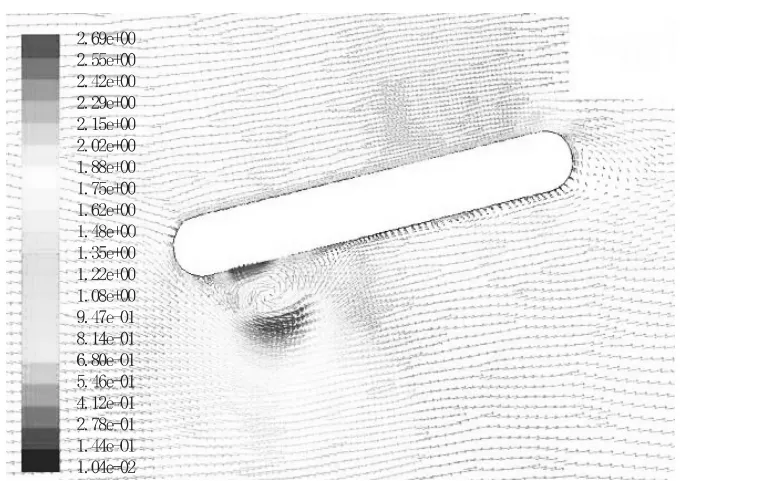
图3 2#槽墩速度矢量图

图4 3#槽墩速度矢量图

图5 4#槽墩速度矢量图

图6 圆柱形槽墩速度矢量图

4 结果分析

1）通过图2～图6可以看出，1#～4#圆端形槽墩偏转一侧出现漩涡，漩涡的位置与流速大小及轴线偏转角度大小均相关，随着槽墩偏转角度增大，漩涡位置往上游方向偏移，流速越大漩涡面积越大，而新方案中圆柱形槽墩漩涡均位于槽墩下游位置，与槽墩相对位置固定。

2）通过表2槽墩阻力系数表统计可看出，随着墙状槽墩偏移角度的增大，槽墩对水流阻力系数呈增大趋势，而新方案中圆柱型槽墩阻力系数远小于墙状槽墩，对水流的阻滞较小，故新方案中圆柱形槽墩水流条件较好。

5 结语

通过方案比选，可见采用单圆柱形槽墩在结构稳定性及对水流影响方面均优于原方案设计中圆端形槽墩。同时，圆柱形槽墩对弯段水流适应性强，槽墩基础设计具有更加明显的针对性。因此，在河道岸线多变、水流条件复杂的河道，跨河建筑物推荐采用单圆柱形槽墩或桥墩。