基于向日葵型圆形光子晶体的高灵敏度太赫兹折射率传感器*

2019-10-25严德贤李九生王怡

物理学报 2019年20期

严德贤李九生王怡

1) (中国计量大学太赫兹研究所,杭州 310018)

2) (中国计量大学信息工程学院,浙江省电磁波信息技术与计量检测重点实验室,杭州 310018)

在基于太赫兹技术的生物化学传感应用中,折射率传感逐步引起了广泛的研究兴趣.为了提升太赫兹传感器的性能,本文提出了基于向日葵型的圆形光子晶体折射率传感器.所设计的传感器包括两个在光子晶体谐振腔中心对称分布的样品池.研究了传感器性能与结构参数之间的依赖关系,并讨论了这些参数的选择从而优化了传感器的性能.最后,所设计的折射率传感器在不同参数下获得的最大灵敏度为10.4 µm/RIU,最大的Q因子为62.21,最大的品质因数为1.46.该项工作将圆形光子晶体传感器扩展到太赫兹波段,实现了高性能太赫兹波折射率传感器.

1 引言

光学传感器,包括温度传感器[1]、湿度传感器[2]和折射率传感器[3]等,可以应用在诸多领域.太赫兹波具有指纹特性,能够区分由分子旋转和振动模式引起的生物和化学物质的特性[4-8].为了提升太赫兹波和分析物之间的相互作用程度,使用具有强约束性的各种微结构来设计传感器,比如光子晶体、纳米线、等离子体结构和超材料等.中国计量大学Cheng等[9]提出了一种新型的基于光子晶体谐振腔结构的传感装置.该传感器是由两个相同的光子晶体板条组成,板条是由在硅基底上按照正方形晶格排列的硅基圆形柱构成.该传感器在529.2 GHz频率处具有较窄的透射共振峰,其品质因数(FOM)为529.深圳大学Xiang等[10]通过激发石墨烯表面等离子共振实现高灵敏度太赫兹气体传感器.优化后的灵敏度约为147°/RIU.Keshavarz和Alighanbari[11]提出了一种基于Tamm等离子体激元的新型太赫兹折射率传感器,由布拉格反射器和石墨烯层组成.该传感器在1.132 THz处的灵敏度为175.5 µm/RIU.斯坦福大学的Padhy等[12]数值研究了基于铜线波导等离子体的太赫兹折射率传感器.获得的峰值灵敏度和分辨率分别为59.9 RIU-1和1.66×10-4RIU,在269.8 µm处的穿透深度为48 µm.Janneh等[13]报道了一种高Q因子超表面太赫兹完美吸收器,并研究了谐振模频率随折射率的变化情况.获得最大的灵敏度和FOM分别为360 GHz/RIU和19.1.

基于二维(2D)光子晶体谐振腔的太赫兹波传感器因其优异的传感性能而被广泛应用于科研及工程领域[14-17].光子晶体是折射率的空间分布具有周期性的人工微结构.由于其具有光子带隙,可用于设计许多的光学器件,如反射镜[18]、偏振选择器[19]和吸收器[20]等等.光子晶体传感器具有无标记传感、高灵敏度、高Q因子和快速响应等优点.根据不同的传感参数,光子晶体传感器可以分为气体传感器[21]、液体传感器[22]、机械传感器[23]和电磁场传感器[24]等.根据不同的传感机理,光子晶体传感器可以分为波长灵敏型、强度灵敏型和相位灵敏型等.光子晶体具有较强的电磁波限制特性,并且谐振腔中产生的谐振模式对周围环境的变化具有较高的灵敏性.

灵敏度是评估太赫兹波传感器工作特性的关键因素之一.研究人员设计了各种传感器结构,如异质结结构[25]、狭缝波导结构[26]和非圆形棒结构[27]等.这些结构比较复杂,在实际应用中不易进行加工,使用成本较高.在红外波区域,基于圆形光子晶体的传感器具有较高的灵敏度[28].但在太赫兹波区域,关于圆形光子晶体传感器的研究尚未见报道.圆形光子晶体具有旋转对称性,这样能够设计出具有更高自由度的太赫兹波器件.基于圆形光子晶体结构的器件具有低损耗、小体积、高Q因子等特性.前期研究结果表明,圆形光子晶体在高性能太赫兹波传感器的应用领域具有较大的潜力.

本文提出了一种基于圆形光子晶体的太赫兹波折射率传感器,空气孔按照向日葵型分布在高密度聚乙烯(HDPE)基底上.太赫兹波沿着传感器入射,并根据透射光谱得到圆形光子晶体的带隙.当中心样品池填充具有不同折射率的分析物时,使用有限元法分析太赫兹波传感器的透射特性.另一方面,还研究了太赫兹波传感器的工作特性.数值计算表明,通过优化结构参数,设计的传感器结构可以分别获得较高的灵敏度(S=10.4 µm/RIU)、Q因子(Q=62.21)和品质因数(FOM=1.46),可以应用于无标签生物传感.

2 模型和理论研究

图1给出本文所设计的基于向日葵型圆形光子晶体太赫兹传感器结构图.在o-xy平面上的散射体(HDPE基板中的气孔)的空间晶格位置由下面公式描述[29]：

其中a是晶格常数,M是空气孔的环数,m (1 ≤m ≤ 6M)是第M圈空气孔的数量.为了降低加工难度和降低传感器成本,所有的空气孔设置在HDPE基底上,空气孔半径为r.HDPE材料在太赫兹波段的折射率为n=1.535.空气孔的深度(与圆形光子晶体基板的厚度相关)在z方向上远大于a.通过移除圆形光子晶体的中心、第一环和第二环处的空气孔,然后将两个较大的对称空气孔作为样品池放置在中心区域从而构成折射率传感器.两个样品池对称分布在圆形光子晶体的中心区域部分.每个样品池是由两个半径分别为r1和r2的圆形空气孔取交集、一个宽度为t的HDPE薄壁以及两个半径分别为R1和R2的圆形空气孔取交集组成.中心缺陷结构可以降低样品填充的难度,同时较大的样品池可以使得太赫兹波与样品充分互作用,提高传感器性能.两个样品池之间的距离定义为g.具有TE偏振态的太赫兹波从光子晶体谐振腔左侧注入到传感器,在传感器的右侧设置监视器,对传感器的透射特性进行监控.所设计的传感器结构参数的初始值设定为：a=100 µm,r=0.42a=42 µm,R1=100 µm,R2=125 µm,r1=80 µm,r2=125 µm,t=10 µm和g=0 µm.

图1 圆形光子晶体太赫兹波传感器 (a)二维结构; (b)三维结构Fig.1.(a) 2D structure of the terahertz wave sensor based on the circular photonic crystal; (b) 3D structure of the sensor.

使用COMSOL Multiphysics软件分析太赫兹波传感器的工作特性.在传感器三维(3D)模型中,空气孔在z方向上的深度d远远大于工作波长(λ)和晶格常数(a),即d ≫ λ,d ≫ a.在仿真过程中,使用2D模型替代3D模型进行计算,从而可以较大程度地减少计算时间和计算内存.根据之前报道的工作,使用2D和3D模型计算所得到结果相似[28],可以获得模型的基本物理特征.本文中模型的边界条件设置为完美匹配层从而吸收能量.模型的网络划分选用物理控制网格,自由网格的数量为227661.当仿真计算机的配置为Intel(R)Core(TM) i5-8400 CPU @ 2.80 GHz和RAM 8.00 GB时,仿真所耗费的平均时间为5227s.

首先仿真计算了无缺陷的圆形光子晶体(蓝色虚线)和本文所设计的传感器(红色实线)在结构参数为初始值时的透射光谱,结果如图2所示.当分析物样品的折射率为n=1.0时,计算频率范围为0.5-2.0 THz的太赫兹波透射光谱.从透射曲线可以看出,当圆形光子晶体没有缺陷时,输入太赫兹波不能够通过传感器.当在圆形光子晶体中引入缺陷构成传感器时,具有特定频率的太赫兹波可以通过传感器部分地到达输出端口,相反,某些频率的太赫兹波不能够通过传感器到达输出端口,这为太赫兹波传感器的实现提供了基础.

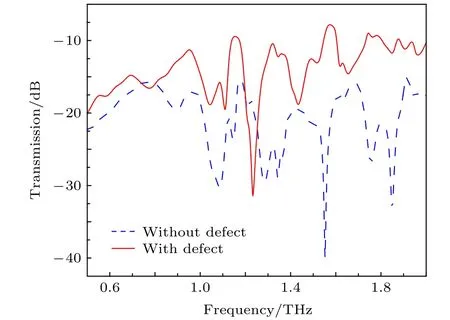
图2 计算得到的无缺陷圆形光子晶体的透射光谱(蓝色虚线)和基于圆形光子晶体设计的太赫兹传感器的透射光谱(红色实线)Fig.2.Calculated transmission spectra of a circular photonic crystal without defects (dashed blue curve) and the designed sensor (solid red curve).

为了评估传感器的性能,本文计算分析了折射率传感器的灵敏度S,Q因子和FOM等性能参数.

灵敏度可以定义为[28]

其中Δλ表示谐振波长的改变,Δn表示折射率的改变.

Q因子可以定义为[28]

其中fR是传输太赫兹波的谐振频率,m是SI单位制的衰减斜率.

FOM是一个表征传感器整体性能的参数,可以定义为[28]

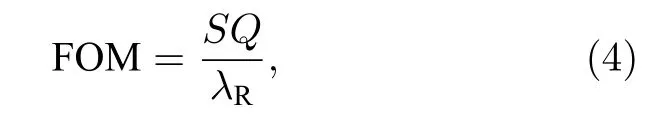
其中S表示灵敏度,Q表示Q因子,λR是谐振波长.

3 研究结果及讨论

为了获得上述的物理量(S,Q和FOM),在图3中,计算了分析物样品折射率n在1.1-1.5变化时在频率范围0.5-2.0 THz内的太赫兹波透射光谱,折射率变化步长为0.1.传感器在填充有不同折射率分析物时的透射光谱呈现出相似的变化趋势,如图3所示.

图3 不同样品折射率时圆形光子晶体传感器在0.5-2.0 THz范围内的透射谱Fig.3.Transmission spectra of the circular photonic crystal sensor ranging from 0.5 to 2.0 THz with different refractive indices of the samples.

图4给出了传感器在太赫兹波频率范围1.15-1.35 THz内的详细的透射光谱.图4的插图是传感器在频率为1.233 THz、折射率为1.0时的2D电场分布,此时入射到传感器的太赫兹波由于散射或者反射,无法到达传感器输出端.随着分析物的折射率n以步长Δn=0.1从1.1增加到1.5,传感器的透射极小值频率从1.233 THz降低到1.220 THz,如图4所示.

图4 圆形光子晶体传感器共振频率1.233 THz附近的透射光谱Fig.4.Transmission spectra of the circular photonic crystal sensor around the selected resonant frequency of 1.233 THz with different refractive indices of the samples.

根据(2)式可以计算得到灵敏度为6.475 µm/RIU.根据(3)式和(4)式,可以获得对应的Q因子和FOM分别为52.57和1.40.该折射率范围表明本文提出的太赫兹折射率传感器可以广泛应用于气体传感或者液体传感领域.

为了提升传感器的传感性能,对包括t和g在内的传感器的结构参数进行了优化.参数t和g对灵敏度S,Q因子和FOM的影响如图5和图6所示.

当传感器的其他参数设置为其初始值时,参数t对灵敏度S,Q因子和FOM的影响在图5中给出.当参数t以Δt=2 µm的步长从0增加到20 µm时,灵敏度从6.975 µm/RIU减小到5.5 µm/RIU,当参数t取值范围在4-16 µm时,灵敏度没有显著的变化.同时,Q因子从49.6振荡增加到62.21.FOM表现出振荡趋势,但没有显著变化,并且介于1.45-1.36之间.应当注意的是,当参数t=20 µm时,两个样品池的面积最小; 而当t=0 µm时,两个样品池的面积达到最大.

图5 当g=0 µm参数t对灵敏度S,Q因子和FOM的影响Fig.5.Influence of t on sensitivity S,Q-factor and FOM when g=0 µm.

图6 当t=0 µm时参数g对灵敏度S,Q因子和FOM的影响Fig.6.Influence of g on sensitivity S,Q-factor and FOM when t=0 µm.

接下来分析当参数t=0 µm时,参数g对灵敏度S,Q因子和FOM的影响,计算结果如图6所示.受到结构参数的限制,两个样品池之间的间隙g位于0-16 µm之间.当g=0 µm时,两个样品池互相接触,中间没有缝隙的存在; 而当参数g增加至16 µm时,两个样品池分别和上、下空气孔相接触,此时两个样品池之间的缝隙最大.当参数g以Δg=1 µm的步长从0 µm增加到16 µm时,灵敏度呈现递增的趋势,并且S从6.975 µm/RIU增加到10.4 µm/RIU.当参数g=16 µm时,最大的灵敏度为10.4 µm/RIU.与之相反,当参数g从0 µm增加到16 µm时,Q因子呈现出递减的趋势,Q因子从49.68降低到33.31.当参数g=0 µm时,Q因子的最大值为49.68.最后,FOM呈现出振荡变化的趋势(尽管不显著),并且其值介于1.43-1.46之间.

从上述结果可以推断出,太赫兹波传感器的结构参数t和g对灵敏度、Q因子和FOM具有不可忽略的影响.灵敏度S和Q因子随着参数t和g的变化呈现显著的变化,并且在不同的参数t和g取值时达到最大值.这主要是由于高灵敏度和高Q因子之间的权衡所造成的.为了获得较高的传感灵敏度,需要满足太赫兹波和分析物之间较高的重叠度,从而能够使得太赫兹波与分析物之间的相互作用增强.与此相反,为了获得较高的Q因子,需要满足太赫兹波与波导介质之间的高重叠度.因此,在实际应用中,应该根据传感需求选择传感器的最佳结构参数.例如,为了实现高灵敏度,传感器结构参数t和g可以分别选择为t=0 µm和g=20 µm.否则,为了获得高Q因子,结构参数t和g可以分别选择为t=20 µm和g=0 µm.而传感器的FOM在参数t和g取值不同时的变化不显著,从而说明本文所设计的传感器的传感性能比较稳定,可以满足不同实际场合的应用需求.目前来说基于HDPE的光子晶体太赫兹波传感器的制造技术主要有3D打印和电子束光刻等.由于实验室没有相应的加工和测试设备,目前条件还无法进行实验验证.