基于支持向量机的坦克驾驶模拟训练结果分析

2019-10-25邓青薛青罗佳

兵工学报 2019年9期

邓青，薛青，罗佳

(陆军装甲兵学院演训中心，北京 100072)

0 引言

随着信息化陆战装备技术含量和复杂程度的不断加大，相应的训练和维修费用也在同步增加。在有限的训练经费条件下，如何提高坦克驾驶员的训练质量成为需要解决的一个重要问题。利用坦克驾驶模拟器开展驾驶训练，可以在保证经济性的同时弥补实装训练准备周期长、训练代价高等缺陷[1]，大大提高训练效率。但在传统的坦克驾驶模拟训练结果分析中，主要是以人为主的定性分析，易受分析人员专业知识、个人偏好的主观影响，对训练结果分析应包含的因素考虑不全，难以对这些影响因素进行有效分类，无法精确指导受训人员进行驾驶操作技能训练。

为解决这一问题，本文利用支持向量机(SVM)对驾驶模拟训练结果进行分析。SVM[2]具有良好的分类能力，已经成功应用于语音处理、文本和图形识别等领域[3-7]。但将SVM应用于坦克模拟训练结果分析并不见多。SVM主要存在二次规划求解计算过于繁琐和核函数参数σ、惩罚因子c[8-9]等超参数选择问题。文献[10]利用交叉试验方法来选择合适的核函数参数和惩罚因子，大大缩小了搜索范围。文献[11]结合遗传算法的全局优化能力和梯度法的局部寻优能力，提出一种基于混合遗传算法的参数选择方法，使SVM具有更好的泛化性能。基于SVM的特点，本文引入粒子群优化(PSO)算法实现SVM超参数的最优选择，并将其应用于坦克驾驶模拟训练结果分析，通过分类得到标准的驾驶操作动作集合，以更好地对受训人员进行指导。

1 坦克驾驶模拟器

坦克驾驶模拟器是一套综合运用多媒体、三维实时成像、计算机仿真、半实物仿真等技术的模拟训练装备，主要用于辅助坦克乘员进行单车驾驶技能训练，同时也可与炮长模拟器、车长模拟器互联组成整车模拟器，用于坦克单车协同训练和坦克分队战术训练。坦克驾驶模拟器主要由驾驶员座舱、软件系统和教员控制台三部分组成。

1.1 驾驶员座舱

驾驶员座舱配有完整的实车操纵件(油门踏板、制动器、操纵杆、离合器踏板等)和仪表、开关、按钮，固定在具有俯仰、侧倾和上下颠震的三自由度液压平台上，可使驾驶员获得与实车一致的感觉。各操纵件在座舱的安装位置、操作空间、操作行程与实装一致，操作力通过测量实车数据，采用弹簧加力的方式实现，从而构建驾驶训练逼真的内部环境。数据采集卡通过编制软硬件接口程序，实现驾驶员操作训练的模拟量信息采集、转换。

1.2 软件系统

软件系统分为图形模块、音响模块、仿真模块、管理模块、液压控制模块、网络模块和检测模块等八部分。图形模块用于实现视景仿真，场景中的植被、道路、建筑等特征要素以三维模型的方式表示，主要效果包括坦克行驶所产生的履带印、扬尘，射击弹着点在地形上动态生成的弹坑，火炮射击炮口焰等。仿真模块运用车辆动力学技术，结合实装的战术技术指标，编写驾驶训练仿真软件，实现车辆的性能仿真，确保加速性、制动性、转向性等跟实装一致。考评模块采用共享内存的方法，记录受训人员的操作数据，并按照教范标准评定训练成绩。音响模块主要用于产生逼真的坦克运动履带声响和发动机噪声。

1.3 教员控制台

教员控制台是管理整个模拟器系统和监控各成员训练过程的控制中枢，装有驾驶员仿真机、管理机及液压控制设备。通过教员控制台可以分别对单台模拟器进行训练科目的设置和下达，也可以统一设置科目进行共同训练或编队驾驶。在训练过程中，可通过选择车辆编号对单台模拟器的操作训练进行实时监控和单独指导。

2 基于自适应粒子群优化算法的超参数寻优

在实际坦克驾驶模拟训练结果分析中，为了获取精确度更高的SVM，需要对超参数进行优化调整。PSO算法有鲁棒性好、收敛快的优点，适合参数寻优，但存在早熟收敛和局部最优的问题。本文提出一种自适应粒子群优化(APSO)算法，采用动态权重参数和多位置查询机制，具有更强的全局优化能力和较高的精度。

2.1 动态权重参数设计

在PSO算法中，用粒子表示优化空间的解，通过粒子适应度值大小判断粒子的优劣。适应度值可由粒子的位置坐标和目标函数得到。在确定粒子初始位置和初始速度后，通过迭代更新粒子的个体最优位置和速度得到最优解。粒子群不断进行迭代优化，在每次迭代优化过程中粒子自动找寻粒子本身最优解和群体最优解两个极值，实现对当前最优粒子的寻求。由(1)式、(2)式得到粒子第d维的更新位置和速度：

(1)

(2)

从上述分析中可以发现，参数选取和收敛性是影响PSO算法性能和效率的重要因素，而ω的选择直接影响算法的收敛性、搜索行为和性能。因此，对ω进行改进是提高算法的关键。

本文针对容易陷入局部最优的情况，设计一种动态权重参数，当粒子目标值发生不同变化时，依据(3)式动态调节ω，以此改良算法的搜索能力。

(3)

式中：ωmin、ωmax分别为ω的最小值与最大值；fi为各粒子适应度；fmin为群体中最小适应度；fa为群体平均适应度。通过调整ω，实现粒子动态自适应。即若fi大于fa，则粒子为优等粒子，赋予其较小的ω可以使其加速向全局最优收敛；反之fi小于fa，则赋予其较大的ω可使其向更好的搜索空间发展、提高局部搜索能力，从而在平衡全局搜索能力的同时改良局部搜索能力。

2.2 多位置查询机制

实现种群中各粒子位置的信息交换是防止早熟收敛现象的主要策略。位置信息交换的核心是探讨利用哪些信息及如何利用信息。研究发现，在PSO算法中存在粒子的极值点，由当前粒子邻域中个体最优位置组成，包含了当前粒子进行位置信息交换的相邻粒子个体信息。极值点不断更新，为粒子提供了较优的搜索区域等启发性信息，从而使得粒子能够沿更好的区域移动。极值点的合理选择将有助于维持群体多样性、防止早熟收敛。因此，可将多位置查询机制的核心问题转化为利用极值点信息，探讨个体最优位置的组成。

(4)

式中：l为当前粒子对应的个数；wl为惯性权重。

2.3 算法参数设置

设定参数少是PSO算法的主要优点之一。然而在实际应用中，这些参数往往对算法的性能和收敛性产生直接而重要影响。目前参数设置多基于实际经验，具体参数如下：

1) 群体规模m，即粒子数目。该参数是决定粒子对搜索空间覆盖程度的关键因素，通常由问题的复杂程度决定。

2) 加速因子c1、c2，即权重值。二者大小分别决定粒子自身经验、社会群体经验对其在搜索空间内移动的影响力度。通常可参考标准PSO算法，取c1=c2=2.

3) 维度D，即问题解的维度。根据对应变量的范围设定，对于求SVM超参数优化而言，维度D取决于所选核函数类型。

4) 适应度函数f(x)，用以反映粒子当前位置优劣的参数。采用训练结果数据分类准确率作为适应度，f(x)=nr/M，nr为正确分类个数，M为待分类总数。

5) 方法终止条件，即一般通过判断最大适应度值或方法达到最大迭代次数。

2.4 基于PSO算法的SVM分类原理

得到超参数最优解后，下一步就是实现SVM分类。首先在权空间中求解如下最优线性函数：

(5)

式中：w为权重矩阵；b为偏倚变量矩阵；e为松弛变量矩阵，e=[e1,e2,…,ek,…,eN]T，k为输入样本数据序列，N为输入样本数据总数；γ为可调参数。

约束条件为

yk[wTφ(xk)+b]=1-ek，

(6)

式中：xk、yk为输入样本数据；φ(xk)为用于样本数据的映射。根据拉格朗日函数可定义：

(7)

式中：α为拉格朗日乘子矩阵，α=[α1,α2,…,αk,…,αN〗T。对上式进行优化，使得L关于w、b、ek、αk的偏导数等于0：

(8)

(8)式满足卡库塔(KKT)条件，可将其转换为矩阵形式所表示的线性方程组：

(9)

式中：H=[1,1,…,1]T；I为N阶单位矩阵；Y=[y1,y2,…,yN]T；

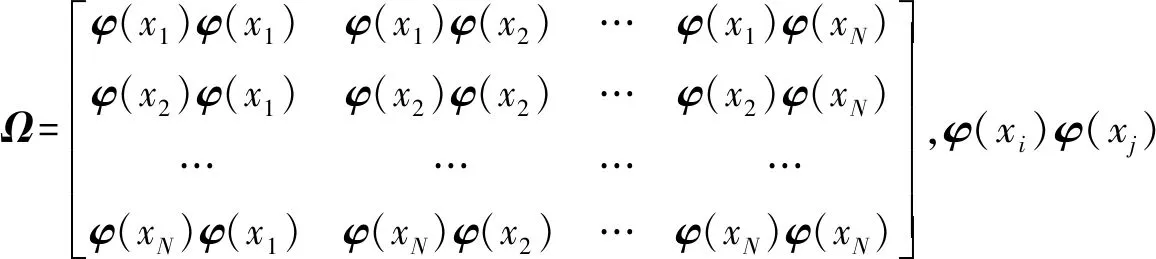
为便于表示，令A=Ω+γ-1I，最终得到α和b分别为

α=A-1(Y-bH),

(10)

(11)

根据α和b的值，对任意输入样本x的分类函数为

(12)

综上所述可以看出，SVM分类将原始空间中的样本映射为高维特征空间中的1个向量，最终将分类过程转化为一个线性方程组求解问题，实现非线性、高维数据的最优特征分类。基于APSO的超参数寻优过程如图1所示。

图1 基于APSO的超参数寻优流程Fig.1 Flow chart of parameters optimization based on APSO

2.5 实验分析

实验中种群规模为50，c1=c2=2，惯性权重最小值为0.15、最大值为0.85，参数σ的搜索范围为[0,10],惩罚因子c的搜索范围为[0,500]。算法终止条件为最大进化代数超过100或连续5代最优解的误差绝对值小于0.02，实验次数为20次，得到结果如表1所示。

表1 两种算法的实验结果比较

从表1中的数据可以看出，采用动态权重参数和多位置查询机制的APSO算法明显优于基本PSO算法。APSO算法得到的最优解比基本PSO更接近Camel函数的全局最小值，表明APSO算法在粒子多样性方面保持较好，不易陷入局部最优，能收敛到最优解。从算法训练误差和训练时间来看，APSO算法收敛速度更快，精度也优于PSO算法，主要在于引入动态权重参数实现了粒子自适应，加快了算法搜索效率。综上所述，本文所提引入动态权重参数和多位置查询机制的APSO算法能有效优化参数选择，在保证收敛精度和速度的同时，能提高种群的多样性。

3 基于SVM-APSO的坦克驾驶模拟训练结果分析

运用SVM-APSO实现坦克驾驶模拟训练结果分析的具体流程如图2所示。

图2 基于SVM-APSO的坦克驾驶模拟训练结果分析流程Fig.2 Flow chart of training effect analysis of tank driving simulator based on SVM-APSO

3.1 数据采集

为便于对坦克驾驶模拟训练结果进行分析，在某型坦克驾驶模拟器的操作件上安装传感器，用于实时记录操作数据。这些数据是受训人员在驾驶模拟训练中操作过程最直接的体现，通过建立数学模型转化为后续的分类特征。数据采集具体包括电源总开关、警报按钮、机油泵按钮、起动按钮的状态数据(0或1)，挡位、油门、主离合器踏板、制动器踏板、左和右操纵杆传感器的测量值，取值范围如表2所示。

坦克驾驶是一项复杂的操作技能。根据实际操作，按训练科目中的驾驶动作组成分为单项操作和组合操作。单项操作是指在驾驶动作中只涉及到一个操纵件的操作。单项操作通常都有明确的动作标准，具有确定性，符合标准即正确，否则为错误。例如打开电源总开关、按下机油泵按钮。组合操作是指单项操作按照不同时间顺序组成的操作序列。组合操作评定比单项操作更加复杂，除单个明确的操作标准，还与操作次序、动作连贯、完成时间等相关联。例如主离合器起车、换挡操作。针对不同操作，需要选取不同特征参数作SVM的输入分量。以2挡换3挡科目训练为例，选择100名1级坦克驾驶员、100名2级坦克驾驶员和100名无等级人员在坦克驾驶模拟器上进行操作。正确操作要领如下：平稳踩下油门至发动机转速2 700～2 800 r/min，迅速松开油门并将主离合器踏板踩到底，将变速杆置于高一个挡位，迅速平稳地松开主离合器踏板，同时均匀地踩下油门。因此，参照操作要领，选择踩油门的快慢、发动机转数、挡位值、松主离合器踏板的快慢、踩主离合器踏板幅度等5个特征参数，其中挡位值、踩主离合器踏板幅度可由传感器直接测量，发动机转数由仿真系统计算生成，踩油门快慢和松主离合器踏板快慢可由传感器测量值计算获得。

表2 各操纵件传感器测量值的取值范围

设s1为t1时刻传感器测量的油门幅度值，s2为t2时刻传感器测量的油门幅度值，则踩油门的快慢v21为

v21=(s2-s1)/(t2-t1)，

(13)

同理，可以计算踩主离合器踏板的幅度p21为

p21=(p2-p1)，

(14)

松主离合器踏板的快慢T21为

T21=(p2-p1)/(t2-t1)，

(15)

式中：p2、p1分别为对应时刻传感器测量的主离合器踏板幅度值。

对于换挡操作，一次变速杆操作涉及两种挡位状态的变化可用g={g1,g2}表示，g1表示换挡前的挡位值，g2表示换挡后的挡位值。

根据以上分析，可以获取300名受训人员的操作数据，并计算获得特征参数如表3所示。

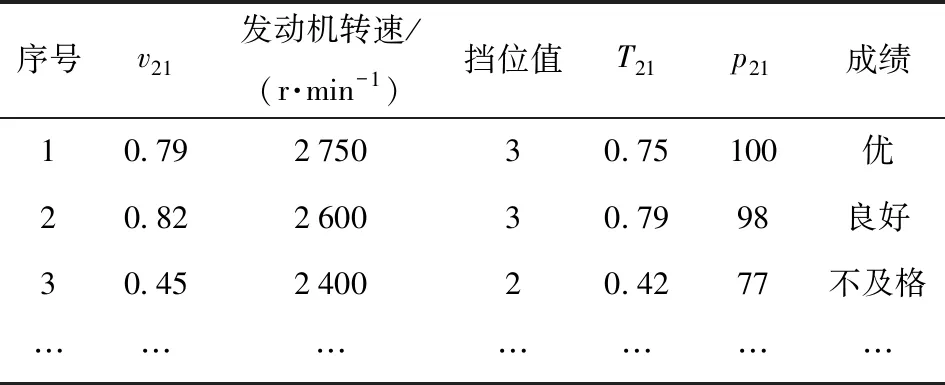
表3 特征参数的计算结果

3.2 数据预处理

表3中含有大量的连续型数据，若用于SVM输入分量则不能很好地提取知识泛化，导致分类结果不好且不利于后续坦克模拟训练结果分析，因此需要进行离散化处理。本文采用文献[12]中的离散化处理方法，得到结果如表4所示。

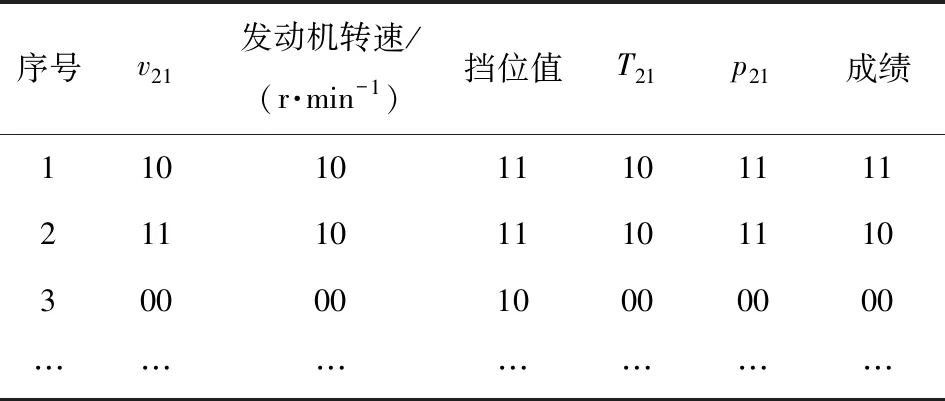
表4 特征参数预处理后的结果

3.3 实验对比分析

在运用APSO选定最优超参数后，采取交叉检验法[13]，从300名人员的训练数据随机选取2/3的样本作为SVM-APSO的输入分量，进行分类器的学习训练。获得决策函数后，将余下1/3的样本作为测试集，输入训练所得到的分类模型。这种随机分组测试共进行20次，得到样本数n与分类结果p的关系如图3所示。对比方法为基于遗传算法的支持向量机(SVM-GA)、传统的SVM-PSO、SVM和决策树C4.5. 实验中种群数为40，交叉概率为0.75，变异概率为0.03，c1=c2=2，惯性权重的最小值为0.15，最大值为0.85，终止代数为100.

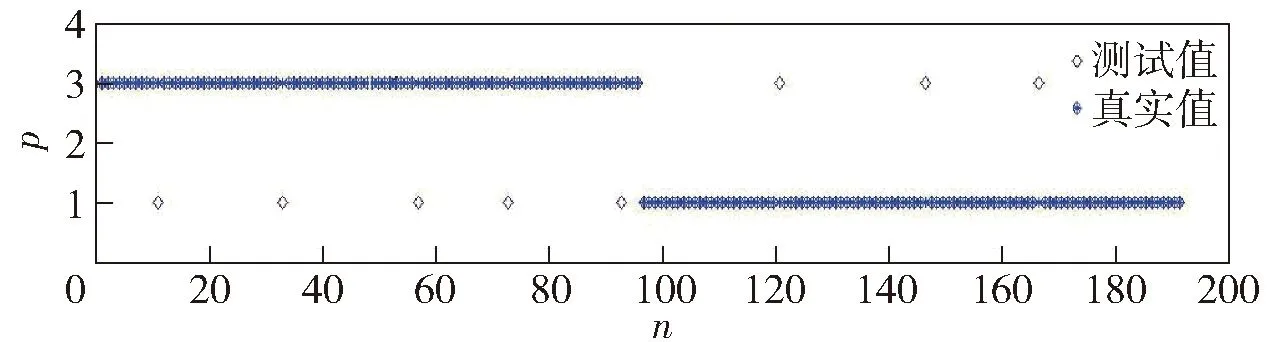
图3 SVM-APSO分类结果Fig.3 Classified results of SVM-APSO

图4 SVM-GA分类结果Fig.4 Classified results of SVM-GA

图5 SVM-PSO分类结果Fig.5 Classified results of SVM-PSO

图6 SVM分类结果Fig.6 Classified results of SVM

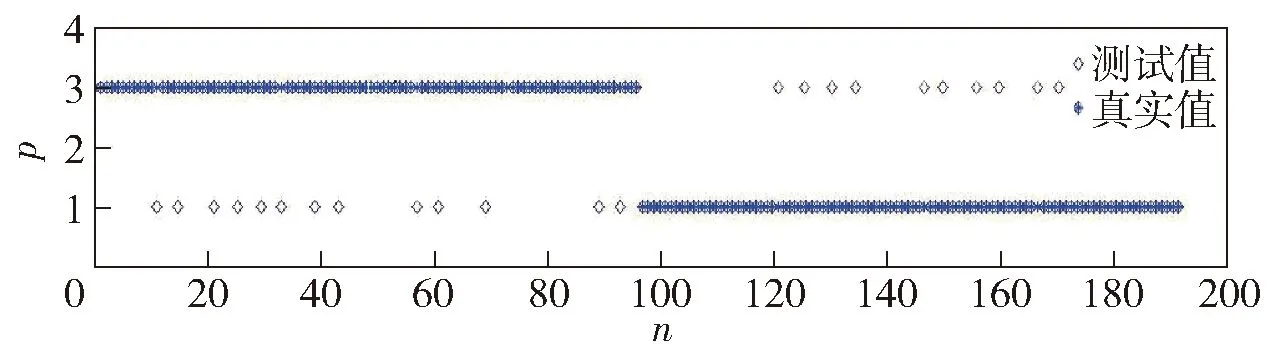
图7 C4.5分类结果Fig.7 Classified results of C4.5

图3～图7分别为采用SVM-APSO、SVM-GA、SVM-PSO、SVM和C4.5分类方法的结果，如果真实值和测试值重合则表示分类结果准确，否则不准确。从图3～图7中可以发现，采用SVM-APSO方法分类所产生的星形符号与四边形重合率高，误分类样本数最少，其他依次为SVM-PSO、SVM-GA、SVM、C4.5，SVM-APSO体现了明显优势，表明所设计的动态权重参数和多位置查询机制维持了粒子的自适应性和多样性，从而实现对参数的自动寻优，有效防止局部收敛，确保找到最优解。而采用SVM-GA需要对分类规则进行编码，通过设计适应度函数对分类规则的有效性进行评价，容易陷入局部最优。SVM-PSO的惯性权重设置固定，当粒子目标值发生动态变化时不能自适应变化，导致全局搜索能力不强。传统SVM未能进行参数优化，误分类数较多。C4.5倾向于不均匀的二分，容易出现过拟合。

为进一步对比分析SVM-APSO、SVM-GA、 SVM-PSO、SVM和C4.5分类方法，选取分类准确率和运行效率两种评价指标。

1) 准确率：算法在测试集上正确分类样本数量与样本总数的比值，通常以百分比表示。

2) 运行效率：算法在运行过程中的时间占用量，通过调用Python中time模块的函数clock()返回当前CPU时间，用来计算分类算法运行的时间。结果如表5所示。

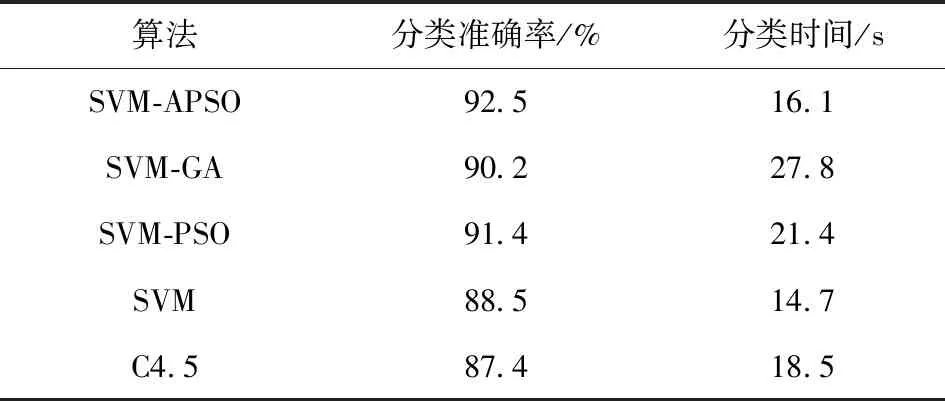
表5 5种算法分类结果比较

从表5中可以看出，SVM-APSO分类准确率比SVM-GA、SVM-PSO、SVM、C4.5都要高，在分类时间上也有明显优势，由于SVM-GA需要循环执行选择、交叉、变异等操作，迭代次数多，消耗时间相对较长。SVM-PSO只采用最优粒子信息进行共享，忽略其他粒子的有用信息，减少了种群的多样性，容易引起早熟收敛，陷入局部最优，增加实验分类误差。传统SVM不涉及参数的最优化过程，所用时间最少，但准确率相比也较低。C4.5易选择取值比较少的特征参数，运算时间较快。而本文所提SVM-APSO采用动态权重参数、多位置查询机制，增加了最优个体数量，扩大粒子共享的信息，保证种群的多样性，同时算法还具有动态自适应性，大大提高了收敛速度，花费的迭代次数较少。综上分析可知，本文所提SVM-APSO方法在精度和时间上有较大优势，表明其在非线性高维数据中实施分类具有精度高、耗时少的优点。

3.4 坦克驾驶模拟训练结果分析

通过运行SVM-APSO模型，对模拟训练结果进行分类，可得到2挡换3挡课目训练成绩优秀所对应的标准操作动作集合[10 10 11 10 11]，即油门操作平衡、挡位正确、主离合器踏板操作符合行程要求，以此作为参考建立起运用技能水平的评价等级，对受训人员的驾驶动作进行精确化分析，可以更好地评估训练质量、提高训练效益。

随机选取一名受训人员的训练数据进行预处理，得到动作集合[11 11 11 01 11]，该受训人员驾驶动作评估为良好，表明其基本掌握驾驶技能，进一步将其与标准操作动作集合进行比较，可以判断受训者在换挡过程中，踩油门过大导致发动机转速过高，另外在换挡后，松离合器踏板过快，不符合前2/3快、后1/3慢的操作要求，总体反映受训者在油门和离合器配合上还不够协调、操作不够熟练，需要对理论知识加强学习，同时进行油门配合的专项强化训练，从而更好地提高训练成绩。

为比较不同层次人员训练，另选取一名受训人员的操作数据[11 11 10 01 00]，表示挡位值为2挡、离合器未踩到底，挂不上挡，成绩为不及格。经了解该受训练人员为无等级人员，与其驾驶水平相符，表明该受训人员掌握动作要领较差，需要在今后训练中加强模拟器基本驾驶动作训练，反复体会换挡要领。