有限理性下群体博弈Nash平衡的稳定性

杨光惠，杨 辉

(贵州大学 数学与统计学院，贵州 贵阳 550025)

群体博弈[1-2]的思想可以追溯到1994年诺贝尔经济学奖获得者John Nash的博士论文[3]有关平衡点的“群体行动”(Mass-Action)解释。其基于代理人的完全理性，以考察群体行为为目的，研究大量的匿名代理人群体的策略互动博弈。这是博弈论研究的一个新兴方向。在经济如公共物品及其外部效应、管理如交通及网络拥堵等领域，群体博弈都有着广泛应用。

然而，在经典博弈及行为等研究中，行为决策者通常是有限理性的[4-6]。这对拥有数量充分大代理人的群体博弈来说更是如此，其中代理人个体并不能达到完全理性的苛刻要求，尤其在实际应用中常常都只是有限理性的。因此，代理人有限理性的合理刻画成为群体博弈论的研究焦点。

2001年，ANDERLINI和CANNING[7]提出了带抽象理性函数的有限理性模型。2006年，我国学者俞教授改进了这一模型[8],其为博弈决策者的有限理性提供了一种较合理的刻画方式，之后这一结果被应用于研究博弈、非线性问题[9-13]及参数最优化问题[14]等。因此，本文将在这一有限理性框架下研究群体博弈的收益函数发生微小扰动时，其Nash平衡的稳定性。

1 预备知识

1.1 群体博弈模型及其中完全理性分析

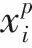
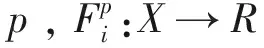
以下是群体博弈{Γ,X,F}的Nash平衡定义：

由此可见，群体博弈的Nash平衡反映了社会Γ中每一博弈代理人个体都是完全理性的。然而,对于拥有大量代理人的群体博弈来说,完全理性这一要求太苛刻了,有限理性才是代理人个体的实际理性表现。因此在群体博弈中开展有限理性的探讨具有重要的理论意义和应用价值。

关于群体博弈Nash平衡的存在性，有，

引理2(定理2.1.1，(p.7))[2]若F:X→Rn连续，则群体博弈{Γ,X,F}在X上至少存在一个Nash平衡。

下面的引理表明群体博弈{Γ,X,F}的Nash平衡与变分不等式的解是等价的，见定理2.3.2(p.42)[2]和引理2.25(p.13)[15]：

1.2 带抽象理性函数的有限理性模型

带抽象理性函数的有限理性模型[7]即模型M=(Λ,X,T,φ):其中Λ为问题空间，X为行为空间，可行集值映射T:Λ×X→2X诱导出集值映射f:Λ→2X且∀λ∈Λ，f(λ)={x∈X:x∈T(λ,x)},理性函数φ:Graph(f)→R+,其描述问题λ∈Λ中的有限理性。特别地，∀λ∈Λ,∀ε≥0，E(λ,ε)={x∈X:φ(λ,x)≤ε}定义为问题λ的ε-平衡集，而E(λ)=E(λ,0)={x∈X:φ(λ,x)≤0}为问题λ的平衡集或最优解集，这对应于问题λ∈Λ中的完全理性。[8]对有限理性模型改进如下:

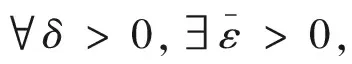
如果平衡映射E:Λ→2X在λ∈Λ连续,称有限理性模型M在λ∈Λ是结构稳定的。

关于有限理性模型的主要结果为下面的定理A[8-9]：

定理A设Λ为完备度量空间，X为紧度量空间,f:Λ→2X上半连续紧值，φ:Graph(f)→R+下半连续，则，

(1)平衡映射E:Λ→2X上半连续且紧值;

(2)存在稠密剩余集Q⊂Λ,使有限理性模型M在每一λ∈Q是结构稳定的;

(3)有限理性模型M在λ∈Λ是结构稳定的, 从而对任意λ∈Q,M在λ对ε-平衡是鲁棒的;

(4)∀λ∈Q，∀λm→λ,εm→0(m→+)，有h(E(λm,εm),E(λ))→0；

(5)如果λ∈Λ,E(λ)是单点集,则模型M在λ处是结构稳定,从而对ε-平衡是鲁棒的。

下面的引理见引理3.2[8]或引理2.5[10]:

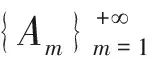
2 有限理性下Nash平衡的稳定性

记Ω={F:F:X→Rn连续}，即具有连续收益的群体博弈全体。∀F,G∈Ω,定义：

显然，ρ为Ω上的距离且空间(Ω,ρ)完备。

现建立群体博弈{Γ,X,F}的有限理性模型M=(Ω,X,T,φ):∀F∈Ω,∀x∈X,可行集值映射T:Ω×X→2X进一步生成集值映射f:Ω→2X且f(F)=X,∀F∈Ω。显然,f(F)=X连续且非空紧值。定义理性函数φ:Ω×X→R+为：

φ(F,X)=maxy∈X〈y-x,F(x)〉。

∀ε≥0，∀F∈Ω,群体博弈{Γ,X,F}的ε-平衡集定义为：

E(F,ε)={x∈X:φ(F,x)≤ε},

其描述了群体博弈中的有{Γ,X,F}限理性。特别地,当ε=0时,上式即为{Γ,X,F}的Nash平衡集E(F,0)=E(F),这刻画了群体博弈{Γ,X,F}中的完全理性。由引理2，E(F)⊆X非空，且称E:Ω→2X为平衡集值映射。

引理5(1)φ(F,X)≥0；(2)x∈E(F)当且仅当φ(F,X)=0。

证明(1)∀F∈Ω，∀x∈X,取y=x∈X，有

φ(F,X)=maxy∈X〈y-x,F(x)〉≥〈x-x,F(x)〉=0.

(2)若φ(F,X)=0，则∀y∈X,有〈y-x,F(x)〉≤0，由引理3，有x∈E(F)。

反过来，设x∈E(F)，由引理3，有〈y-x，F(x)〉≤0，∀y∈X，从而，

φ(F，X)=maxy∈X〈y-x，F(x)〉≤0，

又由(1)知φ(F，X)≥0，故φ(F，X)=0。

引理6φ:Ω×X→R+连续。

证明设∀Fm∈Ω,∀xm∈X，且Fm→F,xm→x(m→+)。只需证明：当m→+时，

maxy∈X〈y-xm,(Fm)(xm)〉→maxy∈X〈y-x,F(x)〉。

定义函数g:X×X→R为：

g(x,y)=〈y-x,F(x)〉,

显然g(x,y)是X×X上的连续函数，因而gm(xm,y)=〈y-xm,(Fm)(xm)〉

是X×X上的连续函数列。于是即需证：

maxy∈Xgm(xm,y)→maxy∈Xg(x,y)(m→+)。

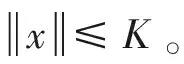
|gm(x,y)-g(x,y)|=|〈y-x,Fm(x)-F(x)〉|

因此，当m→+时，有gm(x,y)→g(x,y)；由引理4，有，

maxy∈Xgm(xm,y)→maxy∈Xg(x,y)(m→+),

所以当m→+时，maxy∈X〈y-xm,(Fm)(xm)〉→maxy∈X〈y-x,F(x)〉成立。

故φ:Ω×X→R+连续。

注2由引理6知群体博弈Nash平衡集是闭的,从而是紧的。

定理1当群体博弈的收益函数发生扰动时，关于其Nash平衡的稳定性，定理A成立。

证明因(Ω,ρ)完备以及X紧，且f:Ω→2X连续，再由引理4-5和注2，故定理A成立。

注3定理1表明在有限理性框架下，大多数群体博弈的Nash平衡都是稳定的。

3 结语

通过建立一个带抽象理性函数的有限理性模型，刻画了群体博弈中博弈代理人的有限理性。研究表明在此有限理性框架下，当收益函数发生扰动时，大多数群体博弈的Nash平衡都是稳定的。其中有限理性函数揭示了群体博弈中的有限理性，这是一种新的刻画方式，与群体博弈已有的相关研究结果是不同的。因此，这不仅为群体博弈中有限理性提供了一种较为合理的理论刻画，也进一步推广其实际应用。本课题今后将开展多目标框架下群体博弈中有限理性刻画研究。