约束型双钢板混凝土组合剪力墙滞回性能的分析

2019-10-24袁朝庆章桀王忠全蒋光耀计静张宇

石河子大学学报（自然科学版） 2019年5期

袁朝庆，章桀，王忠全，蒋光耀，计静，张宇

(东北石油大学土木建筑工程学院/黑龙江省防灾减灾及防护工程重点实验室，黑龙江大庆 163318)

为提高钢管混凝土柱的延性并且防止钢管混凝土柱的剪切破坏，Tomii等[1]、周绪红等[2]先后提出了钢管约束钢筋混凝土柱的概念，其相对于普通钢管混凝土柱，钢管约束混凝土柱的最主要特点是钢管在柱上下端与梁连接的节点处开一定宽度的缝隙，使钢管与上下梁端分开，可保证外包钢管在轴向压力作用下不会直接承受竖向荷载，外包钢管主要用来为核心混凝土提供横向的约束作用，如图1所示。大量研究表明，同截面尺寸下钢管约束钢筋混凝土柱与普通钢管混凝土柱相比，钢管约束型钢筋混凝土柱具有优良的抗震性能，可有效提高钢筋混凝土短柱的受剪承载力、延性和耗能能力，尤其在较高轴压比下构件的水平受剪承载力提高且延性大幅改善。

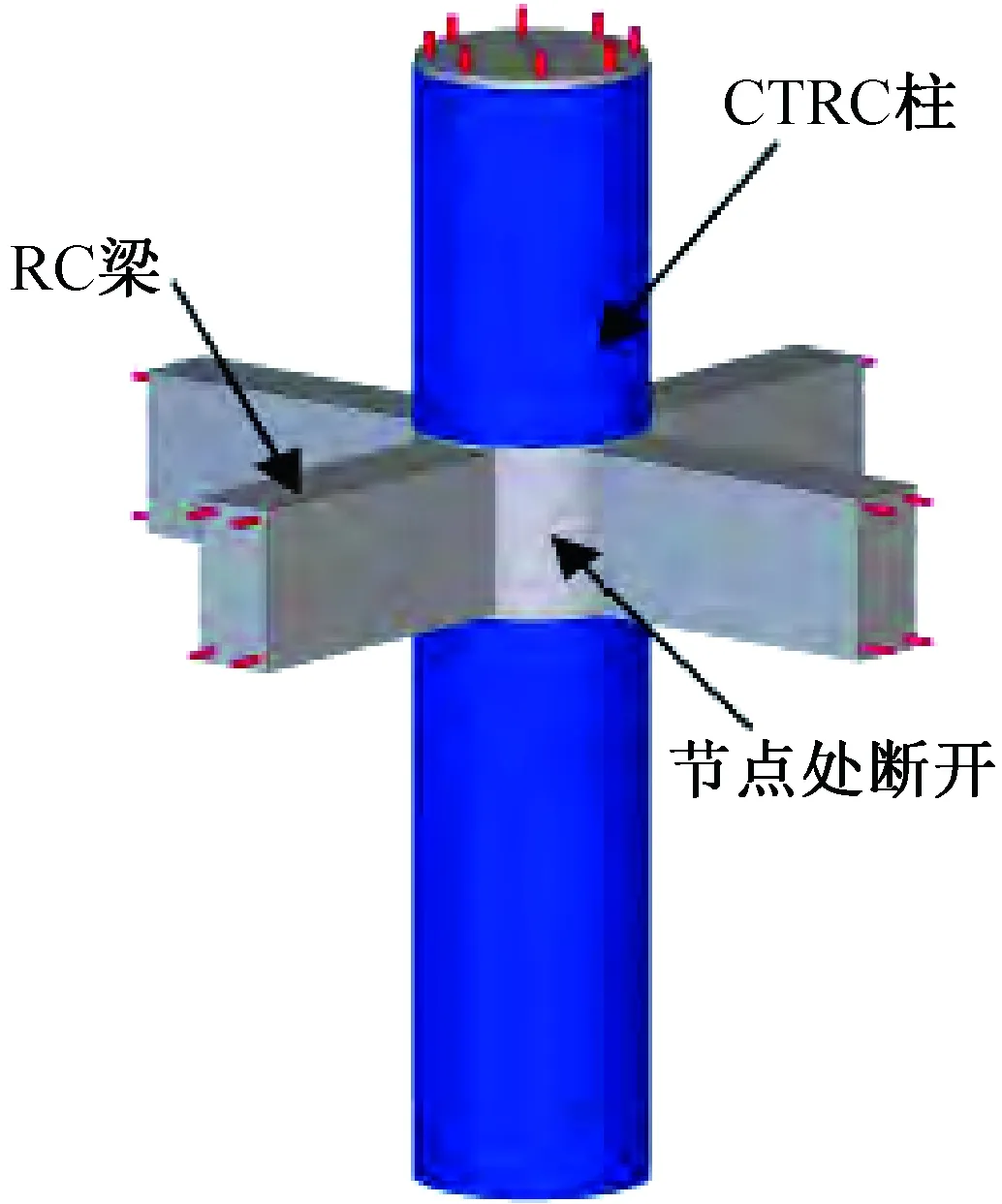
图1 钢管约束钢筋混凝土柱Fig.1 Steel pipe constrained reinforced concrete column

图2 约束型双钢板混凝土剪力墙示意图Fig.2 Constrained double-steel concrete shear wall

由已有研究可知，当组合剪力墙在轴压比较大时破坏较早，延性较差，因此，本文考虑将钢管约束混凝土柱的理论引用于双钢板混凝土组合剪力墙，在组合剪力墙上部与楼板交接处截去一定高度的外包钢板，形成约束型双钢板混凝土组合剪力墙，如图2所示。Tae-Sung Eom[3]等对采用焊接钢筋连接的墙体截面为矩形和T形的双钢板混凝土组合剪力墙进行了低周往复加载试验，试件的最终破坏模式为剪力墙底部或连梁端部的钢板焊缝拉断，钢板局部屈曲。墙体底部的加强措施对试件的变形能力影响较大，但由于端柱未设置边缘约束构件其延性较低。国内学者对双钢板混凝土组合剪力墙结构以试验研究居多，有限元分析和理论分析较少。聂建国等[4-6]对双钢板混凝土组合剪力墙进行了大量的试验研究，其研究内容主要研究了轴压比与剪跨比对组合墙抗震性能的影响、组合剪力墙的变形能力与压弯承载力并提出压弯承载力的数值模型和简化计算公式，此外对外包多腔钢板-混凝土组合剪力墙抗震性能的试验研究结果表明，双钢板混凝土组合剪力墙结构承载力高、延性好，适用于高层和超高层建筑中。本研究团队对不同轴压比的情况下约束型钢板剪力墙以及约束型开洞双钢板剪力墙的研究[7-8]结果表明，相较于普通组合剪力墙，约束型剪力墙的承载力、延性、耗能能力得到大幅提高。本文将利用有限元方法进一步分析约束型双钢板混凝土剪力墙的滞回曲线、骨架曲线、承载能力、延性、刚度退化、耗能能力等滞回性能。

1 有限元模型的验证

为验证利用有限元软件分析双钢板混凝土组合剪力墙滞回性能的可行性，本文选取文献[9]中的DCS1试件作为对比分析对象，使用有限元软件ABAQUS建立与文献中试验构件尺寸完全相同的有限元模型，分析其在与文献[9]试验中相同加载方式下的滞回性能，并与试验结果进行对比分析。

本文分析模块采用ABAQUS/Standard，钢板与混凝土采用三维实体单元(C3D8R)，钢材本构选用四折线模型[10]，混凝土采用塑性损伤模型[10]。钢板与混凝土之间相互关系采用粘结滑移[11]，法向行为设置为“硬接触”，切向行为设置为“罚”接触；模型底部设为完全固定，模型顶部忽略加载梁；设置参考点，并将整个上表面与参考点耦合，在参考点上施加竖向荷载和水平位移荷载[10]，约束墙体面外屈曲[10]。

有限元模型如图3所示，并命名为DCSW1*。

图3 有限元模型Fig.3 finite element model

图4和图5分别为DCSW1和DCSW1*的滞回曲线和骨架曲线。由图4、图5可看出：

(1)有限元模拟出来的滞回曲线与试验滞回曲线形状相似，但是有限元模拟的滞回曲线更加饱满。

(2)在弹性阶段，有限元模拟和试验结果相比，两者的初始刚度符合的比较好；在弹塑性阶段，有限元模拟结果的在达到其屈服点之后结构的承载力均大于试验值。究其原因主要是由于模拟时认为材料是均匀的，但是实验过程中使用的材料存在气泡孔隙等，焊接技术对其也有影响，试件存在初始缺陷，而有限元难以模拟出这种真实的材料属性和混凝土压崩等真实的实验现象。

(3)总体而言，有限元模拟结果与试验结果的最大误差为6.59%，因此，应用ABAQUS模拟双钢板混凝土组合剪力墙在往复荷载作用下的滞回性能是合理可行的。

图4 试验和仿真滞回曲线图对比图Fig.4 Experimental and simulation hysteresis graph comparison chart

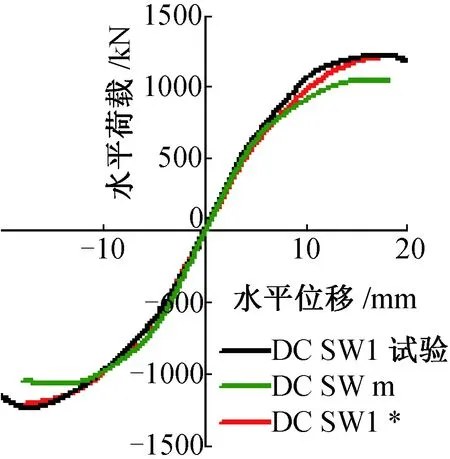
图5 骨架曲线对比图Fig.5 skeleton curve comparison chart

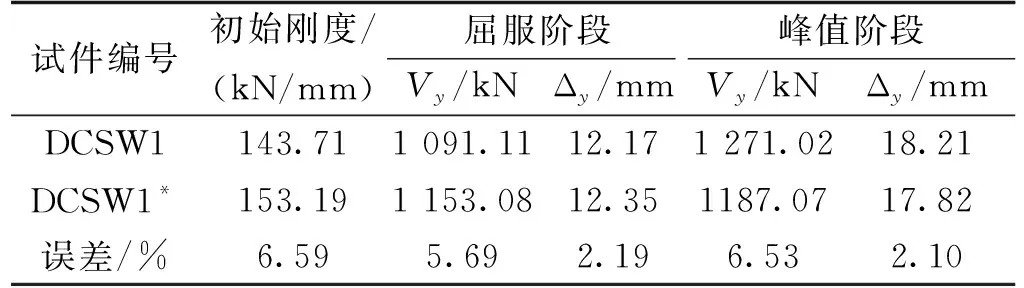
试件编号初始刚度/(kN/mm)屈服阶段峰值阶段Vy/kNΔy/mmVy/kNΔy/mmDCSW1143.711 091.1112.171 271.0218.21DCSW1*153.191 153.0812.351187.0717.82误差/%6.595.692.196.532.10

注：表中所列结果均为平均值。

2 有限元模型的建立

为了对比分析在高轴压比情况下约束型双钢板混凝土组合剪力墙与普通双钢板混凝土组合剪力墙滞回性能的差异，本文所有剪力墙的轴压比均为0.5。首先，利用ABAQUS建立一个普通双钢板混凝土组合剪力墙模型作为参考模型，命名为Base。Base模型层高取2700 mm，截面尺寸为1200 mm×200 mm，钢板厚度取为8 mm。

为了分析约束型双钢板组合剪力墙中预留缝隙的最优宽度，在Base模型基础上保持其他参数不变仅改变外包钢板的高度形成HS(Height of Steel)系列的4个约束型双钢板混凝土剪力墙模型，分析其滞回性能。其有限元模型依次命名为HS1、HS2、HS3、HS4，分别代表其余参数不变和外包钢板上部分别截去剪力墙高度的1%、2%、3%、4%。

钢材采用Q345，混凝土采用C30。Base边界条件同上节DCSW1。具体有限元模型及模型尺寸见图6，混凝土采用塑性损伤模型[12]，钢材本构关系参照文献[12]，采用的水平位移加载方式和钢材本构如图7所示。

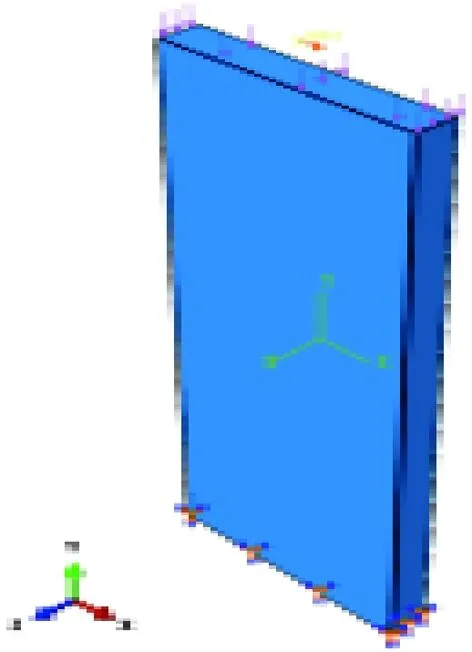
图6 有限元模型Fig.6 finite element model

图7 加载方式和钢材本构Fig.7 Loading method and steel constitutive

3 结果与分析

3.1 水平荷载-位移曲线对比分析

3.1.1 滞回曲线

图8为模拟得到的1个Base模型和4个HS系列模型的底部剪力-顶点位移滞回曲线图。由图8可见：

(1)整体上，剪力墙的滞回曲线光滑，呈现梭形，正反两个方向基本对称，但是随着剪力墙开缝宽度的增大，HS系列约束型剪力墙的滞回曲线变得光滑饱满，同时承受水平力达到峰值后下降的速度变慢，下降段不明显。

(2)HS系列约束型剪力墙承载和变形能力变大，延性很好，具有良好的抗震性能。说明普通剪力墙Base的屈服位移和破坏位移均小于约束型组合剪力墙，钢板与混凝土材料的组合，由截去部分高度钢板使得该组合在承受竖向荷载时拥有更加优秀的变形能力，与约束型组合剪力墙的延性相比，普通型组合剪力墙得到了不同程度的提高，其中开2%和3%缝时效果较好，在2%和3%时该约束型钢板混凝土组合剪力墙能更加有效利用钢板材料的性能。这表明HS约束型双钢板混凝土组合剪力墙能够大幅提高构件的延性，当开缝宽度为3%时效果最佳。

(3)HS系列约束型组合剪力墙的滞回曲线达到峰值点后滞回曲线下降的速度变慢，下降段不明显，其中HS2和HS3与其他HS系列约束型双钢板混凝土剪力墙相比，滞回曲线最为饱满，耗能能力最为出色，承载力达到峰值荷载后下降速度最为缓慢，说明后期刚度最大。

图8 不同缝宽的组合剪力墙滞回曲线Fig.8 Hysteresis curve of combined shear wall with different slit width

3.1.2 骨架曲线

不同缝宽的组合剪力墙骨架曲线(图9)显示：

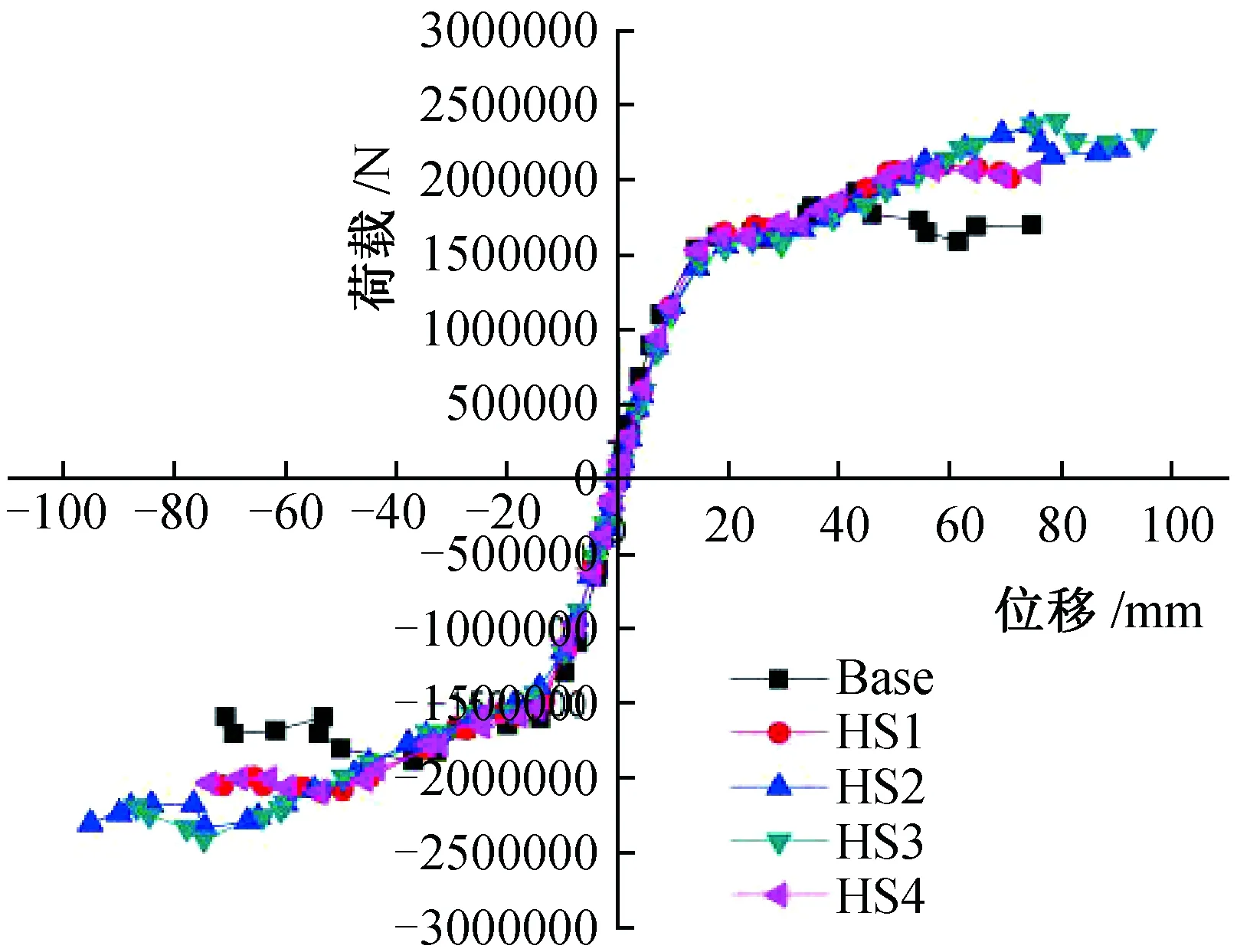
图9 不同缝宽的组合剪力墙骨架曲线Fig.9 Combined shear wall skeleton curve with different slit widths

(1)骨架曲线的形状相似，大致呈S形，说明整个试件在受力过程中经过弹性阶段、弹塑性阶段、承载力下降阶段3个阶段。

(2)在加载初期，试件处于弹性阶段各个剪力墙的骨架曲线基本重合，斜率刚度相近，结构尚未进入塑性。随着水平荷载的增加，当结构达到屈服后，相较于Base组合剪力墙，HS系列约束型剪力墙的峰值位移后于Base普通双钢板剪力墙出现，并且承载力略高于Base剪力墙，同时2种剪力墙的下降段下降速度也有所不同，Base剪力墙的下降段更为陡峭，下降速度更快。这表明HS系列约束型剪力墙的延性要好于Base普通剪力墙。

(3)HS2和HS3剪力墙和其他剪力墙的屈服位移几乎同时出现，峰值位移和极限位移却大幅滞后，峰值荷载也远大于其他HS系列约束型剪力墙。说明HS2和HS3剪力墙延性和承载能力最好。

3.2 承载能力对比分析

名义屈服点和极限点的选取方法参照文献[12-13],本文采用割线刚度法求屈服点，极限点取峰值荷载下载到85%对应的位移点，表2给出了各个试件各个特征点的荷载。由表2可知：4种剪力墙的屈服荷载分别较Base剪力墙提高了3.15%、2.56%、1.12%、1.28%，4种剪力墙的峰值荷载分别较Base剪力墙提高了10.04%、23.48%、26.03%、9.35%。这说明在高轴压比下HS系列约束型剪力墙能够有效地提高构件的承载力，其中HS3提高的幅度最大，即开缝81 mm的效果最好。

表2 各试件承载力特征点的有限元结果Tab.2 Finite element results of bearing capacity characteristics of each test piece

3.3 延性分析

延性δ=Δu/Δy，其计算结果(表3)显示：普通剪力墙Base的屈服位移和破坏位移均先于约束性剪力墙出现，屈服点层间位移角和破坏点层间位移角均小于HS系列约束型剪力墙，值得注意的是，与Base剪力墙相比，其峰值位移和极限位移有了一定的提高，主要其延性性能相较于Base剪力墙效果明显，开缝1%、2%、3%、4%时，剪力墙的延性分别提高了17.8%、51.7%、57.2%、16.3%，可见HS系列约束型剪力墙的变形增大，刚度下降，但是构件的延性得到了大幅提高，当开缝宽度为3%时效果最佳，起到了更好的约束作用。

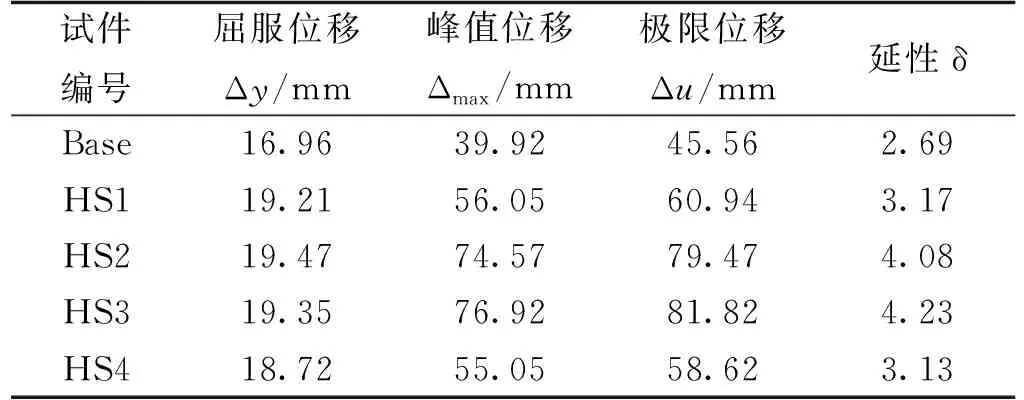
表3 各试件变形能力有限元分析结果Tab.3 Results of finite element analysis of deformation capability of each test piece

3.4 刚度退化

本文采用割线刚度来描述往复荷载作用下剪力墙构件的刚度退化现象，割线刚度计算方法参考文献[14-15]。由计算结果(图10)可知：

(1)各剪力墙试件刚度退化趋势大致相同，随着位移的增加，刚度不断减小。对HS系列试件，除了在弹性阶段HS4比其他HS系列约束型剪力墙刚度略有提高，其他阶段曲线近乎重合，这说明开缝宽度对约束型剪力墙的刚度退化的影响很小。相比于Base构件，HS系列约束型剪力墙在弹性阶段刚度小于Base剪力墙，但是刚度退化速度也更缓慢；构件屈服至加载后期，随着位移的增加，HS系列约束型剪力墙刚度的刚度退化曲线和Base构件的曲线近乎重合，之间的刚度数值和退化速度近乎相同。

(2)对于HS系列约束型剪力墙，前期剪力墙刚度退化速度较快，加载后期剪力墙的刚度退化曲线变化幅度较为平缓。其原因主要是：加载前期，水平位移较小，核心混凝土的横向应变小于钢板的横向变形，钢板对核心混凝土的约束较小，导致前期刚度衰减幅度较大；加载后期，随着位移荷载的增大，混凝土的横向应变大于钢板的横向变形，钢板对核心混凝土的约束逐步增大，钢板对混凝土形成了有效约束，从而导致后期刚度退化曲线变化趋于平缓。

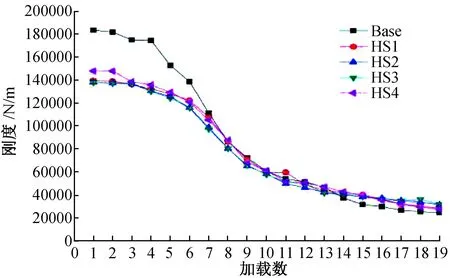
图10 刚度退化曲线Fig.10 stiffness degradation curve

3.5 耗能能力对比分析

量化结构耗能能力的指标有很多，本文采用等效粘滞系数he定量分析剪力墙的耗能能力[16]，图11和12是各工况等效粘滞系数he随层间位移角增大的变化曲线。

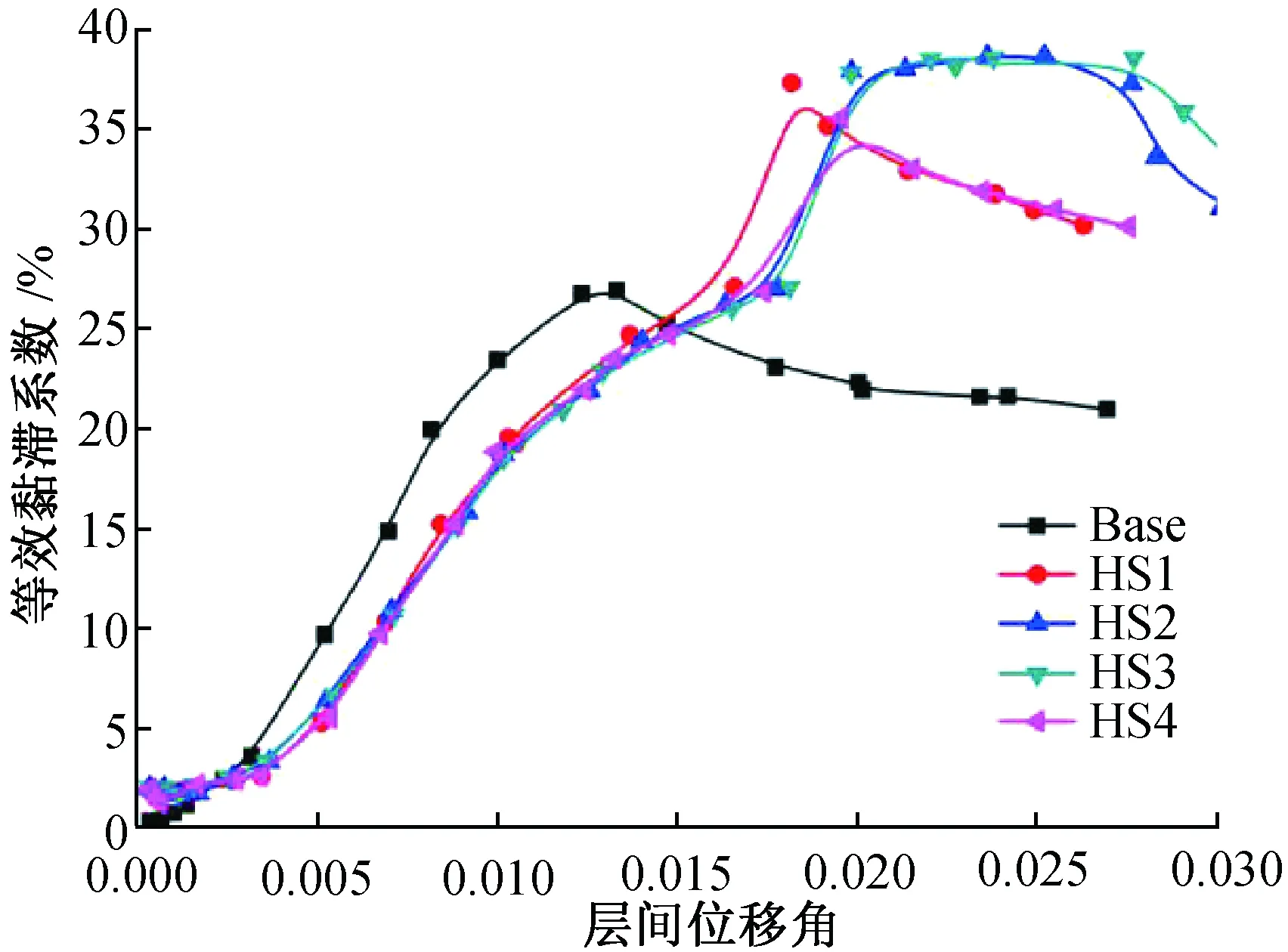
图11 等效黏滞系数与层间位移角关系曲线Fig.11 the relationship between the equivalent viscous coefficient and the interlayer displacement angle

图12 耗能-层间位移角关系曲线Fig.12 Energy consumption-interlayer displacement angle curve

由图11和图12可以看出：

(1)剪力墙的等效黏滞系数约在0.2～04，在未屈服前，试件的等效黏滞系数普遍偏低，屈服以后等效黏滞系数迅速增长至峰值后递减。

(2)HS系列约束型剪力墙和Base普通双钢板混凝土剪力墙的耗能在初始阶段基本重合，但是等效黏滞系数相差较大。在层间位移角θ达到0.015之前，与普通剪力墙Base相比，HS系列约束型剪力墙的等效黏滞系数和耗能一直小于Base普通剪力墙；随着层间位移角的增大(θ大于0.015)，模型进入塑性程度加深，HS系列约束型剪力构件的等效黏滞系数和耗能逐渐增大至峰值，而Base剪力墙等效黏滞系数却不断减小，HS系列约束型剪力墙的等效黏滞系数相比Base普通剪力墙得到了大幅提高。这是因为在加载前期水平位移较小，核心混凝土的横向应变小于钢板的横向变形，钢板对核心混凝土的约束较小，而随着水平位移荷载的增大，模型进入塑性程度加深，混凝土的横向应变大于钢板的横向变形，钢板对核心混凝土的约束逐步增大，钢板对混凝土形成了有效约束，从而导致HS系列约束型剪力墙构件的耗能能力和安全性能得到提高。

(3)对于HS系列约束型剪力墙，随着层间位移角的增加，试件耗能不断提高，进入弹塑性阶段后，各试件累积耗能呈指数增长趋势。表明HS3约束型剪力墙相比其他HS系列约束型剪力墙，具有更好的耗能能力和安全性能。