基于决策树优化的BP 神经网络在海参养殖产量预测中的应用

李海涛，刘泰麟

（青岛科技大学信息科学与技术学院，山东 青岛 266061）

随着刺参Apostichopus japonicus 养殖等水产养殖业的发展，养殖方式正在朝着科学、智慧的方向发展。自身的产业特点和刺参养殖的经验性和专业性使预测刺参养殖产量面临巨大挑战。科学的预测方式能指导相关人员合理调整养殖产业结构，在一定程度上促进水产养殖行业的发展。目前，科学的预测方式主要采用相关性分析、SWM（支持向量机）、多元回归、灰色模型、神经网络模型等算法预测水产养殖产量，如基于灰色新陈代谢GM（1，1）模型的中国水产品年总产量的预测[1]、基于灰色马尔可夫修正模型的水产品产量预测[2]，以及对虾相对产量预测的人工神经网络模型[3]等。与其他预测模型相比，BP 神经网络是最高效和适用的方法之一，尤其是对非线性的、规律性弱的刺参养殖活动数据，应用BP 神经网络进行预测可以得到理想的预测结果。然而，传统BP 神经网络模型在选择输入层神经元和确定隐含层节点数量方面存在不足，在对非平稳序列、非线性和相关关系复杂、预测精度要求高的刺参养殖产量预测中，容易出现训练时间长、学习效率低、易陷入局部极小、预测精度低等问题[4]，限制了其应用和扩展。

为了解决上述问题，本文研究设计一种基于C4.5 决策树优化的BP 神经网络刺参养殖产量的预测模型，利用决策树降低输入层神经元维度，加快BP 神经网络收敛速度，提高产量预测的精准度。

1 数据与方法

1.1 数据来源

以山东省刺参养殖年产量预测为例。为使最终结果更加切合实际结果，本文在数据选择上参考现有的水产养殖相关文献[5]，得出海参养殖产量受气候、环境条件、养殖政策、养殖技术、经济效益等多种因素的影响，在此基础上，最终选定年平均水温（X1）、育苗量（X2）、养殖面积（X3）、灾害经济损失（X4）、养殖技术推广人数（X5）、海参损失数量（X6）和专业养殖劳动力（X7）作为初始输入条件属性，海参养殖产量预测为决策属性（Xk）。海参养殖相关数据来自《中国渔业统计年鉴2017》[6]；海水环境数据来自国家海洋环境预报中心网站。

1.2 数据预处理

采用归一化方法对模型输入数据进行数据预处理，在训练集的选取上涵盖最大最小特征值，避免测试集的数据越界。将各要素统一到［0，1］区间，减少不同要素取值范围差异过大而忽略小数值数据价值[7]。线性归一化公式和还原公式如下:

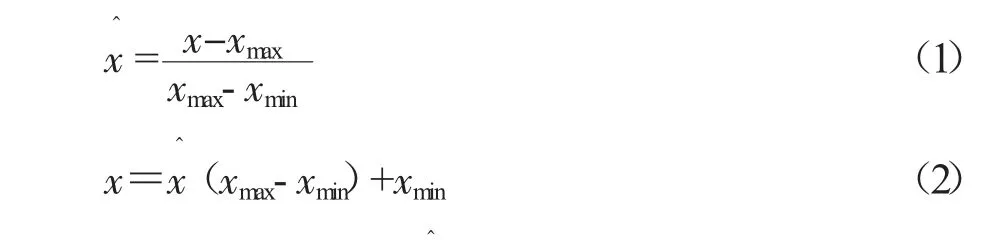
上述两式中，x 和x分别为输入条件属性数据归一化前和归一化后的值，xmax和xmin分别是该属性因素序列中的最大值和最小值。

1.3 C4.5 决策树算法与二分分割算法

C4.5 决策树算法能克服数据要求高、参数复杂、计算繁琐等困难，可以根据既定规则完成基本的决策任务[8]，具有良好的分类和预测能力，广泛应用于数据挖掘中。C4.5 决策树算法的原理如下：

设S 是类样本的数据训练集，m 是训练集中的类别数量，Si为S 中第i 类样本的数量，i=1,2,......,m，即：

此时训练集S 的信息熵H（S）为：

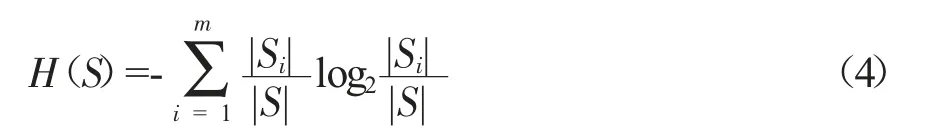
式中，训练集S 被属性A 的属性值划分为m 个子集，i=1,2,......,m，|Si| 表示第i 个子集中的样本数量，|S|表示划分前数据集中样本的总数量。

根据属性A，令={S1,S2,…,Sn}，其中n 为属性A包含不同值的数目。于是，训练集在属性A 上的信息熵为：

信息增益率为：

“二分分割算法”是使区间的两个端点逐渐向零点逼近，以得到零点近似值的方法[9]。基本思想如下：

（1）确定隐含层节点数的近似范围，假设范围是[1，10]。

（2）将s1=1、s2=10、s3=（s1+s2）/2=6（四舍五入）分别带入训练网络，用同一组样本数据、同样的转移函数、训练函数进行训练，分别比较不同隐含层节点数在神经网络训练下的输出均方误差（MSE）。

（3）计算三个不同节点数输出的均方误差，假设s1输出误差为E（s1），s2的输出误差为E（s2），s3的输出误差为E（s3）。如果E（s1）＞E（s2），则将隐含层节点数范围压缩至[s3，s2]。如果E（s1）＜E（s2），则将隐含层节点数范围压缩至[s1，s3]。连续压缩区间范围，直至均方误差最小节点数即为所需要的隐含层节点数。

1.4 BP 神经网络

BP 神经网络是模拟人类大脑神经网络的结构和特性构建的网络模型，具有良好的学习和归纳能力，已广泛应用于各类预测模型中[10-14]。神经网络可以很好地模拟刺参养殖产量及相关影响要素间的关系，把输入、输出问题转化为非线性映射，解决因缺乏精确计算公式而导致海参养殖产量预测精度低的问题[9]。BP 神经网络的建立包括三个过程：网络初始化、正向传递和反向传递。具体算法步骤如下：

（1）输入学习样本（Xi，Y）i（i=1，2，...，n），Xi和Yi分别是学习样本的输入参数和输出结果；

（2）确定各层的神经元数量，随机在两层神经元之间建立连接权重矩阵，Mo代表第1 层和第L+1 层的连接矩阵，表示每层的输出值；

（4）比较各输出节点的均方误差：

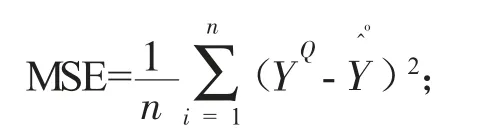
（5）判断是否符合原定误差ε，如果满足要求，则结束，否则进入步骤6；

（7）转至步骤4，直到结果的均方误差在允许的误差范围之内。

2 刺参养殖产量预测模型构建

在BP 神经网络模型基础上，根据已知样本数据，通过决策树的分类选择方法过滤多余输入条件属性，取最简属性集合作为神经网络输入节点构建神经网络，用“二分分割算法”来确定隐含层节点数量，并在输入条件属性和海参养殖产量之间建模（图1）。

通过样本数据训练，获得预测网络，经测试、调整，即可用于预测刺参养殖产量。具体实施步骤如下：

（1）对网络的权重、阈值、收敛精度和最大迭代次数进行初始化；

（2）通过决策树依次获取信息增益率最高的属性，结合模型情况确定网络最佳条件属性集合；

图1 刺参养殖产量预测模型建立过程Fig.1 Establishment of prediction model for sea cucumber production

（3）通过二分分割算法快速计算确定隐含层节点数量；

（4）确定优化的BP 神经网络结构，进行网络训练；

（5）进行网络测试，检查训练是否达到预期精度，若达到预期精度或达到最大迭代次数，停止并获取网络的输出结果。

3 刺参养殖产量BP 神经网络预测模型的应用分析

3.1 输入神经元优化

输入BP 神经网络进行训练的数据通常包含很多属性，其中有些属性与目标能力无关或影响很小。输入属性太多时，会降低神经网络收敛速率，而增加过度拟合的可能性。因此，在将属性数据输入神经网络进行训练前，要根据目标能力对属性进行约简，选择合适的输入属性，确定BP 神经网络的最优输入属性集合。计算训练数据后，比较各个属性的信息增益率是选择C4.5 决策树分类选择最佳输入属性的方法。依信息增益率大的属性或者属性集合确定网络的初始输入。以收集的初始输入条件属性数据为基础，经C4.5 决策树算法计算相关条件属性的信息增益率（表1）。

上述条件属性的信息增益率表明，年平均水温（x1）、养殖面积（x2）、育苗量（x3）、海参损失数量（x4）的条件属性信息增益率均大于10%，对海参养殖产量影响比较大，作为最优特征组合和神经网络的输入变量。

表1 条件属性信息增益率结果Tab.1 Results of conditional attribute information gain rate

表2 不同隐含层节点数神经网络性能的比较Tab.2 Performance comparison of neural networks with number of nodes in different hidden layers

3.2 BP 神经网络设计

BP 神经网络输入层神经元，即经决策树分类优先特征选择算法后的年平均水温、养殖面积、育苗量、海参损失数量四个影响产量的条件数据。网络转移函数采用Sigmoid 函数[15]，即：

为提高模型收敛速率，减少误差，避免陷入局部极小，本模型采用Delta 学习规则[16]使误差信号的目标函数最小：

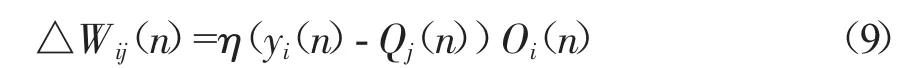
式中，△Wij（n）表示当输入向量为xn时神经元i和j 之间的连接权值，η 和yi分别表示学习效率和神经元i 的期望输出值，Oi和Qj分别表示神经元i和神经元j 的激活值。经实验，取η 为0.50，误差容量为0.0001，训练次数为500。

已有研究表明，目前还没有成熟的理论依据支持精确地确定隐含层节点数量，很多研究还是根据以往的经验公式得到一个确定的值[17-20]。常见的经验公式如下：

上述三个公式中，C、m 和n 分别表示隐含层节点数、输出层神经元数和输入层神经元数，a∈[1，10]。

根据经验公式可以得到隐含层节点数，但是其经验性太强，误差太大，预测结果不够准确。本文经过经验公式粗略计算，得出隐含层节点数的范围为[3,10]，再结合“二分分割算法”计算得出不同隐含层节点数对应的网络性能数据（表2）。

由表2 可知，当隐含层节点数为6 时，神经网络总体性能最高。所以，确定本文神经网络模型的最佳隐含层节点数为6；隐含层节点数有无限个的单隐层BP 神经网络可实现任意的非线性映射[21]。因此，本文网络模型中隐含层的层数为1。设计BP神经网络预测模型的拓扑结构为4-6-1（图2）。

图2 BP 神经网络预测模型的拓扑Fig.2 Topology of BP neural network prediction model

3.3 BP 神经网络设计预测结果对比分析

为检验优化后的BP 神经网络模型的性能，随机选取五组数据带入本文训练好的模型进行产量预测，并与传统的BP 神经网络和灰色GM（1,1）预测结果进行比较（表3）。

用均方误差（MSE）来评估本文BP 神经网络模型与传统的BP 神经网络以及灰色GM（1,1）预测模型的性能。结果表明，MSE 的值与模型的预测精度成反比。公式如下：

本文模型与传统BP 神经网络预测模型和灰色GM（1,1）的学习速率的差异对比结果见表4。

对比结果表明，本文模型预测结果的均方误差比传统BP 神经网络模型和灰色GM（1,1）分别减少了0.05 和0.12，均方误差更小；网络运行平均耗时也有所缩短。本文模型能在较短时间内获得较高精度的预测结果。

表3 不同预测方法对不同年份产量的预测结果比较Tab.3 Comparison of forecast production by various prediction models in different years

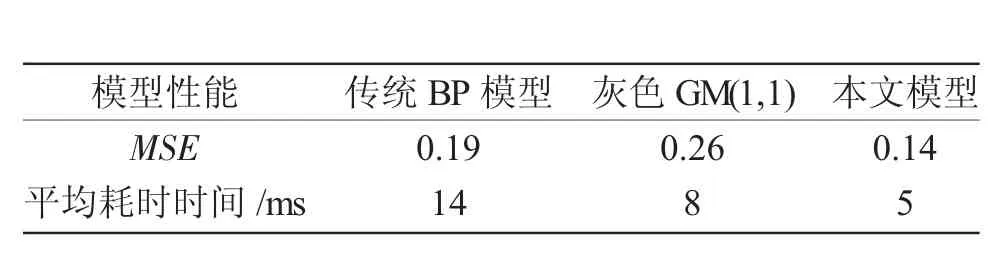
表4 不同预测模型性能的比较Tab.4 Comparison of performance of different prediction models

4 结论

利用BP 神经网络结合C4.5 决策树算法对刺参养殖产量历史数据进行训练，形成的网络模型预测刺参养殖产量误差变小、平均耗时缩短，可以满足刺参养殖产量预测的精度要求。优化后的BP 神经网络数据训练分析模型可以应用到对虾养殖产量预测、养殖水质预测、养殖病害预测等研究，具有一定的扩展性和推广价值。