船舶推进轴系弯—纵耦合效应的非线性振动特性

徐鹏，邹冬林，吕芳蕊，塔娜，饶柱石*

1 海军驻大连船舶重工集团有限公司军事代表室，辽宁大连116005

2 上海交通大学 振动、冲击、噪声研究所，上海200240

3 上海交通大学机械系统与振动国家重点实验室，上海200240

0 引 言

作为船舶动力装置的核心部件，推进轴系可以将主机功率转化为螺旋桨的推力，然后经推力轴承传递给船体，从而推动船舶前进。在螺旋桨流体激励、转轴不平衡激励、轴承摩擦激励等复杂的外部载荷作用下，运转中的推进轴系将不可避免地发生振动现象。过大的振动易导致轴系疲劳失稳、轴承磨损甚至是损坏，从而影响轴系的安全稳定运行，因此，船舶推进轴系的振动特性一直是该领域的研究热点［1-2］。推进轴系振动包括弯曲振动、扭转振动和纵向振动3 种形式。目前，国内外大多采用线性理论研究推进轴系，故可分别独立开展3 种振动的分析计算，从而简化模型。例如，李全超等［3］研究了船舶推进轴系的弯曲振动特性，重点分析了支撑参数对弯曲振动特性的影响规律；李燎原等［4］研究了船舶横摇条件下，主机隔振对推进轴系弯曲振动特性的影响；Zhang 等［5］研究了船舶推进轴系的纵向振动特性；张金国等［6］分析了推力轴承几何参数对轴系纵向振动特性的影响规律；胡泽超等［7］研究了利用共振转换装置控制推进轴系纵向振动的优化设计方法；张阳阳等［8］分析了推进轴系的纵向振动特性和振动控制策略；Polic 等［9］研究了螺旋桨与冰相互作用下的轴系扭转振动响应；谈微中等［10］开展了大型船舶推进轴系扭振特性的仿真和试验研究。上述研究均是基于线性理论展开，然而，在实船复杂的工况条件下，这3 种振动形式之间会产生强烈的耦合作用，例如，轴系弯扭耦合振动、多频现象、组合共振、自激振动等。因此，为了避免工程设计隐患，有必要建立推进轴系的非线性动力学模型。

对于船舶推进轴系不同方向之间的耦合非线性振动，国内外已开展了相应的研究工作。例如，Hua 等［11］、花纯利［12］和张振果等［13］分析了推进轴系在水润滑橡胶轴承摩擦激励下的弯扭耦合振动现象，以及轴承摩擦导致自激振动的发生条件。刘宗发等［14］研究了由螺旋桨偏心导致的轴系弯扭耦合振动现象，并分析了轴系疲劳应力。朱汉华等［15］研究了润滑耦合冲击作用下的轴系弯扭耦合振动特性。Jiang 等［16］研究了因摩擦激励导致的推进轴系弯—纵耦合振动现象。近年来，这方面的研究成果层出不穷，由此可见，轴系非线性效应对其振动特性的影响已经引起了业内重视。

在上述研究中，非线性效应都是由于存在非线性激励源（例如，摩擦激励）所致；而在实际工程应用中，几何大变形也会导致轴系的非线性效应。对小型船舶的推进轴系而言，其刚度较大，几何非线性效应很小。然而，大型船舶的推进轴系一般很长（可能上百米跨度）且细长比较小（细长比即轴系截面回转半径与轴系长度之比，细长比越小，表明轴系越“柔”，这是工程中考察梁刚度的一个重要指标），其在螺旋桨流体激励和不平衡载荷激励下，容易产生较大的轴系横向变形，进而在纵向变形和横向变形之间产生较严重的弹性耦合作用，这就是大变形几何非线性导致的梁弯—纵耦合振动现象。基于此，本文拟建立并求解船舶推进轴系的弯—纵耦合非线性动力学方程，然后采用有限元法和多尺度法分析推进轴系产生弯—纵耦合非线性效应时的异常振动现象，用以为大型船舶推进轴系的工程设计提供参考。

1 船舶轴系的弯—纵耦合非线性动力学模型

典型的船舶推进轴系由螺旋桨、后艉轴承、前艉轴承、中间轴承及推力轴承组成，如图1 所示。本文假设轴系具有均匀截面，并将螺旋桨简化为集中质量，各轴承简化为弹簧与阻尼。

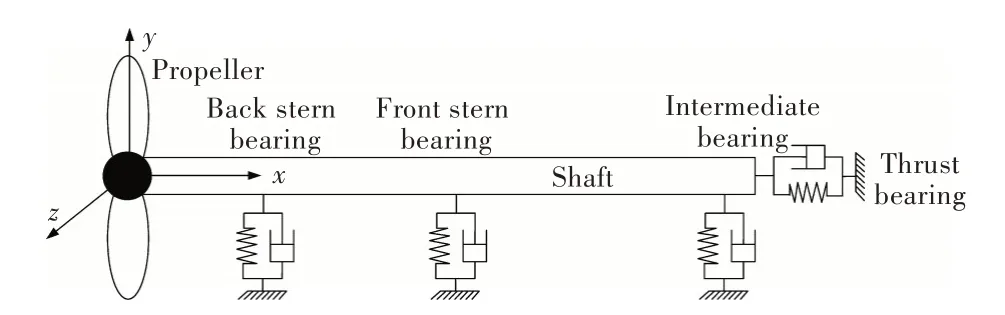
图1 船舶推进轴系简图Fig.1 Schematic of marine propulsion shafting

采用瑞利梁力学模型，利用Hamilton 变分原理建立考虑弯—纵耦合非线性效应的推进轴系振动偏微分方程［17］：

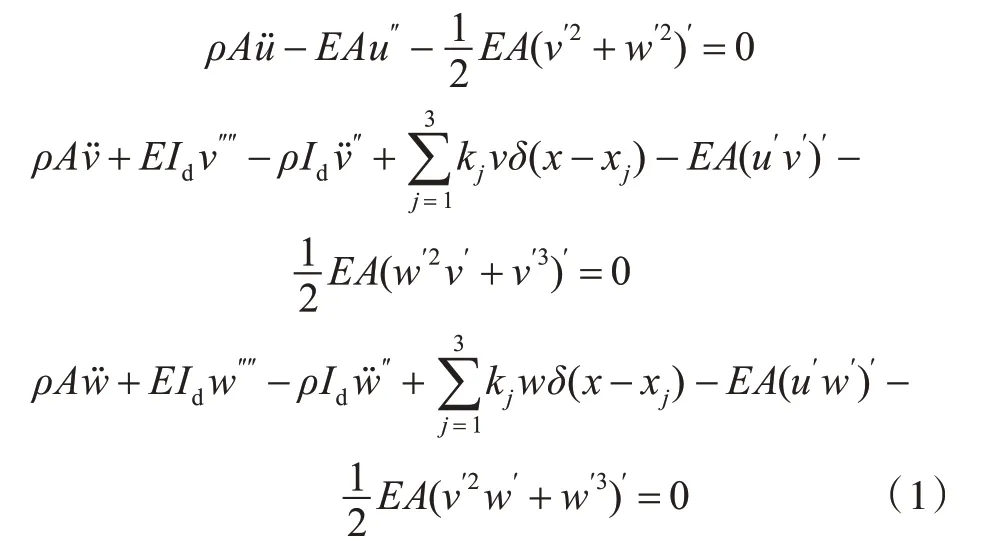
式中：ρ为轴段密度；A为轴段横截面面积；u，v，w分别为轴系的纵向（x向）、横向（y向）、垂向（z向）振动位移；E为弹性模量；Id为截面惯性矩；kj为各径向轴承的刚度，其中j=1，2，3；x为轴系的纵向距离；xj为螺旋桨到各径向轴承的纵向距离；δ(x)为狄拉克函数。

式（1）列出了弯—纵耦合引起的非线性项：第1个方程最后一项的物理意义为轴系发生弯曲变形时，导致纵向方向产生的附加作用力；第2 个和第3 个方程倒数第2 项的物理意义为轴系发生纵向变形时，导致弯曲方向产生的附加作用力；第2个和第3 个方程最后一项的物理意义为轴系产生较大的弯曲变形时，横向变形与垂向变形相互耦合产生的附加作用力。如果忽略这些非线性项，式（1）即可简化为轴系的线性振动偏微分方程。

式（1）中，轴系首尾两端需满足的力平衡边界条件为

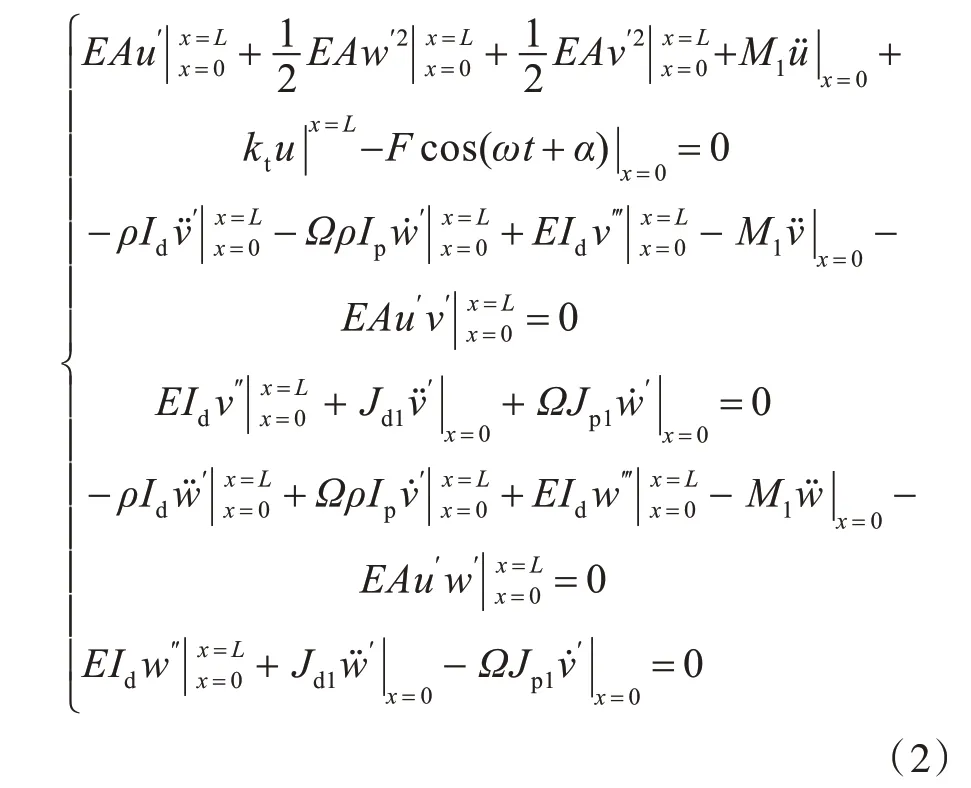
式中：L为轴系长度；M1为螺旋桨质量；kt为推力轴承的刚度；F为外激励载荷；t为时间；α为载荷相位；Ω为转轴旋转速度；ω=7Ω，为叶片次激励频率转速（7 叶桨）；Ip为转轴截面极惯性矩；Jd1为螺旋桨径向转动惯量；Jp1为螺旋桨极转动惯量。

式（2）中：第1 个方程表示纵向力平衡；第2 个和第3 个方程分别表示横向剪力平衡与弯矩平衡；第4 个和第5 个方程分别表示垂向剪力平衡与弯矩平衡。同样，如果忽略非线性项，式（2）即可简化为轴系线性振动偏微分方程所需满足的力平衡边界条件。

2 非线性方程的求解方法

对于式（1）和式（2）所示偏微分方程的定解问题，可以采用有限元数值方法进行求解［18-19］，也可以进一步降维之后采用多尺度近似解析方法来求解［17］。有限元数值方法的求解过程较简单，适用于任意几何形状的轴系，具有一定的通用性；但该方法属于数值方法，难以获得系统的解析解，故无法揭示某些机理性的规律。而多尺度法属于渐进解析法，因而可以获得非线性系统的解析解，但其求解过程较复杂。本文将同时采用这2 种方法进行求解：在第3.1～3.3 节利用有限元法分析系统产生弯—纵耦合效应时的振动现象；在第3.4 节利用多尺度法分析轴系相关参数对系统弯—纵耦合效应的影响规律。

2.1 有限元法

对式（1）和式（2）应用有限元理论，即可推导出单元质量矩阵Me、陀螺矩阵Ge和单元刚度矩阵Ke，其中Ke包含（线性刚度矩阵），（一次位移刚度矩阵）和（二次位移刚度矩阵）。Me，Ge及的构成与线性情况完全一致，故此处不再列出具体形式，仅列出非线性刚度矩阵和。

式中，a～f和～等系数详见文献［19］。

将轴系各单元的Me，Ge，Ke组装在一起，考虑集中质量、支撑弹簧及阻尼的影响，即可得到轴系弯—纵耦合效应的振动微分方程：

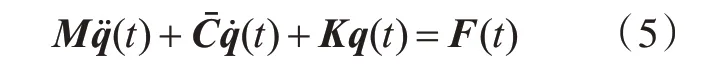
式中：q(t)为位移向量；Cˉ=ΩG+C，其中C为阻尼矩阵；F(t)为载荷向量。

可以采用Newmark法等数值积分方法求解式（5），当系统非线性较弱时，通过减小步长即可取得很高的求解精度。但如果系统的非线性较强，即使步长很小且计算量很大，其求解精度也无法令人满意，此时，可以结合Newton-Raphson 方法进行求解：首先，通过Newmark 法得到该时间步下的近似解，然后通过Newton-Raphson 方法进一步搜索得到更精确的数值解［18］。如果需得到系统的周期解，还可以结合打靶法，详见文献［19］。

2.2 多尺度法

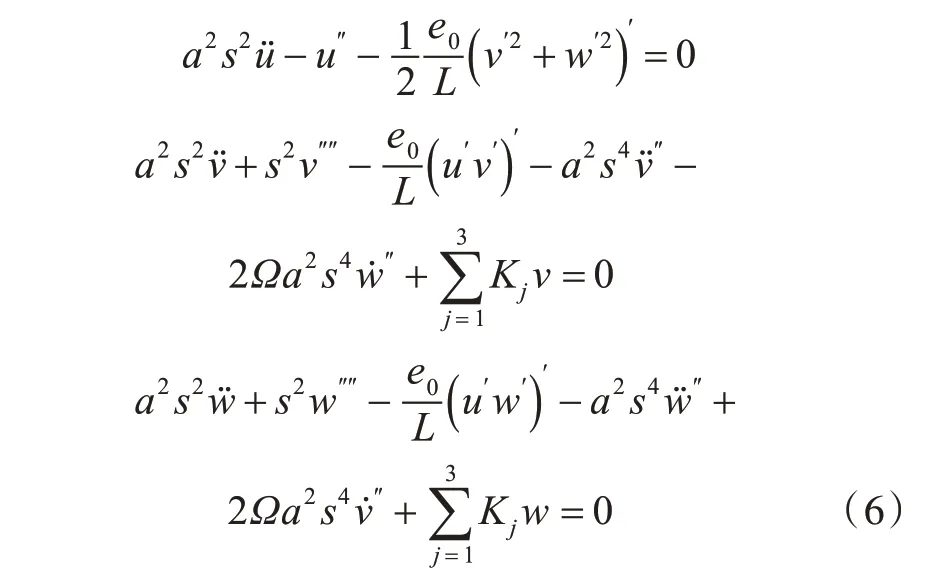
利用Galerkin 方法即可将式（6）所示的偏微分方程转化为常微分方程，其中试探函数将采用线性模态振 型。设u(x，t)=φ1(x)X1(t) ，v(x，t)=φ1(x)Y1(t) ，w(x，t)=ψ1(x)Z1(t) ，其中：φ1(x) 为纵向第1 阶模态振型；φ1(x)为横向弯曲第1 阶模态振型；ψ1(x) 为垂向弯曲第1 阶模态振型；X1(t) ，Y1(t)，Z1(t)分别为时间尺度上的纵向、横向及垂向振动位移。将其代入式（6），结合边界条件并引入模态阻尼，得

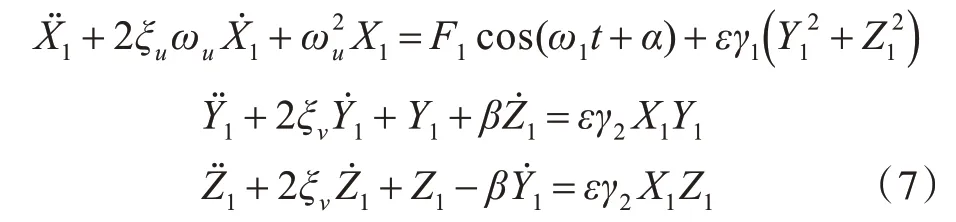
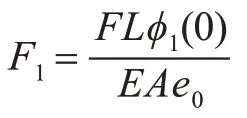
式（7）是基于变分原理，并结合Galerkin 方法而得到的。实际上，针对能量泛函，采用Ritz 法结合Lagrange 方程也可以得到式（7），具体详见文献［20］。采用多尺度法和经典龙格库塔方法［21］求解式（7），即可得到轴系弯—纵耦合作用下的非线性振动特性。

3 弯—纵耦合效应对轴系振动特性的影响

本节将阐述弯—纵耦合效应对轴系非线性振动特性的影响，例如，多频现象、跳跃现象及能量迁移现象等，并将简单分析轴系各参数（例如，各支承轴承、螺旋桨质量、轴系细长比等）对弯—纵耦合非线性强弱程度的影响。

3.1 多频响应现象

对于线性系统，稳态响应的频率成分始终与激励力保持一致；然而，对于非线性系统，响应中除了激励力频率成分之外，还可能出现别的频率成分，即多频响应现象。以表1 所示的推进轴系为研究对象，利用上文介绍的有限元方法进行求解。

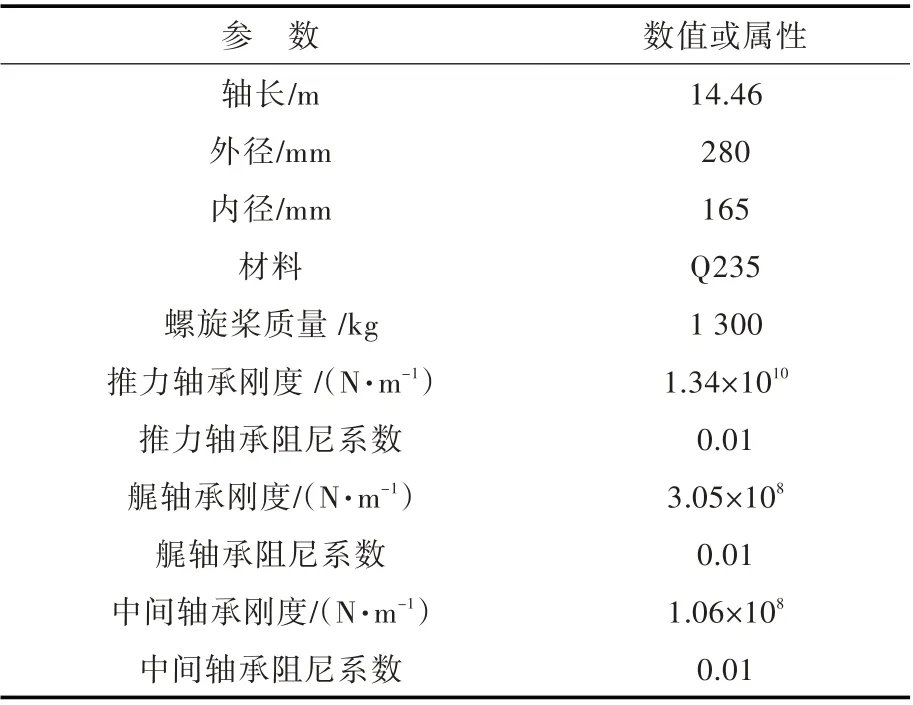
表1 推进轴系的主要参数Table 1 The main parameters of propulsion shafting

假设轴系的纵向叶频激励频率f纵=23.3 Hz，横向叶频激励频率f横=20 Hz。利用Newmark 法并结合Newton-Raphson 法计算轴系的振动响应，选取轴系中点处响应的时域与频域为考察对象，计算结果如图2 所示。

从图2 中可以看出，尽管横向与纵向均为单频激励，但考虑弯—纵耦合非线性效应之后，响应中除了激励频率成分之外，还出现了其他新的频率成分（表2）。

由此可见，即使仅存在单频激励，轴系弯—纵耦合非线性效应也会使其出现多频响应现象，新的频率成分为激励频率的各种组合，而组合形式主要与非线性的阶次和响应乘积有关。由式（1）可知，轴系弯—纵耦合的非线性阶次主要为二次和三次，且以弯曲响应和纵向响应的乘积为主，因此，新的频率成分也表现为激励频率的2 倍或3倍，而响应中的乘积关系在频谱中则体现为激励频率的相加与相减。

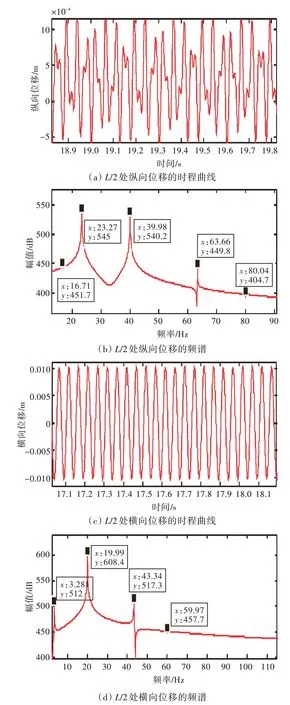
图2 轴系L/2 处振动响应时域与频域曲线Fig.2 Time domain and frequency domain response at L/2 of shafting

表2 响应中新的频率成分组合Table 2 The new frequency components in the response

笔者所在团队曾测试了数艘在役舰船的推进轴系振动响应，根据测试结果，上述多频响应现象是真实存在的。

3.2 跳跃响应现象

本节将利用有限元法结合打靶法进行求解［19］。轴系升速与降速时，叶频激励力作用下的轴系幅频响应曲线如图3 所示。从图中可以看出：1）弯—纵耦合效应呈“硬弹簧”特性，故轴系的共振频率略大于线性固有频率；2）在某些频率点处，响应曲线同时存在3 个解（2 个稳定解和1 个不稳定解），所以存在跳跃现象。

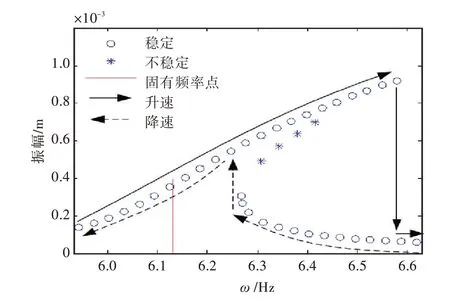
图3 叶频激励下的轴系幅频响应曲线Fig.3 Amplitude frequency response curves of shaft under blade frequency excitation

从物理的角度分析，弯—纵耦合非线性效应会导致轴系产生正的非线性刚度，并叠加在原来的线性刚度上，从而增加轴系的共振频率。

图4 所示为不同阻尼比和细长比时的轴系幅频响应曲线（图中，σ为频率失调参数，且7Ω-ε2σ=wf，其中wf为轴系横向第1 阶正进动固有频率）。从图中可以看出，阻尼比越小、细长比越小时，轴系弯—纵耦合的非线性效应越强。因此，可以通过增加阻尼比来抑制几何非线性效应，从而提高轴系的稳定性。

3.3 能量迁移现象

众所周知，对于线性振动而言，各个方向的振动具有相互独立的特点，互不干涉。但是对于非线性振动而言，其各个方向的振动之间则可能存在能量迁移现象。如图5 所示，当轴系存在弯—纵耦合效应时，在某些特定工况下，弯曲振动与纵向振动之间存在能量渗透。图5 中：au为纵向振动幅值；av为弯曲振动的正进动幅值；bv为弯曲振动的反进动幅值。在计算过程中，仅在纵向方向施加激励力，而弯曲方向没有载荷［20，22］。从图中可以看出，对于临界载荷f2：当激励力小于f2时，随着激励力的增加，纵向振动幅值也线性增加，弯曲振动幅值为0，这与线性振动的结论一致；当激励力大于f2时，随着激励力进一步增加，纵向振动幅值不变，能量饱和之后，多余的能量将转移到弯曲方向，进而导致弯曲振动幅值进一步增加。同时，正进动与反进动之间的能量分配与其进动频率成反比［22］，因此反进动的幅值大于正进动。

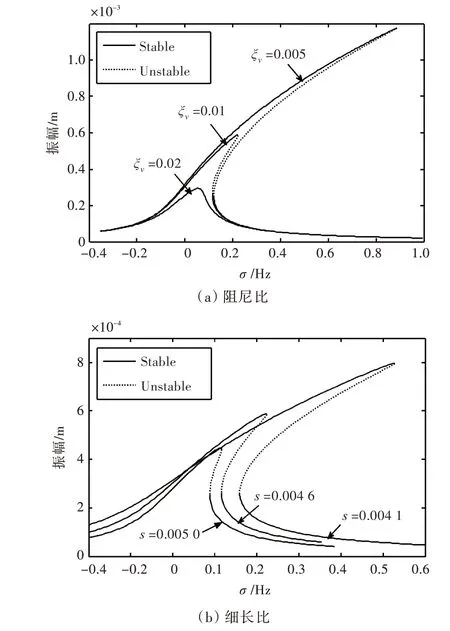
图4 幅频响应曲线随阻尼比和细长比的变化规律Fig.4 Variation of amplitude frequency response curves with damping ratio and slenderness ratio

临界载荷f2与系统参数、激励频率及非线性强弱程度等密切相关，图6 所示为临界载荷f2随系统阻尼比的变化规律。从图中可以看出，随着阻尼比的减小，临界载荷f2也随之减小，这表明在很小的激励力作用下也可发生能量迁移现象。

在设计推进轴系时，为了有效控制轴系纵向振动，可以充分利用这种能量渗透特性，使纵向振动幅值保持在一个“极限值”，而不会随纵向激励力的增加而进一步增加。

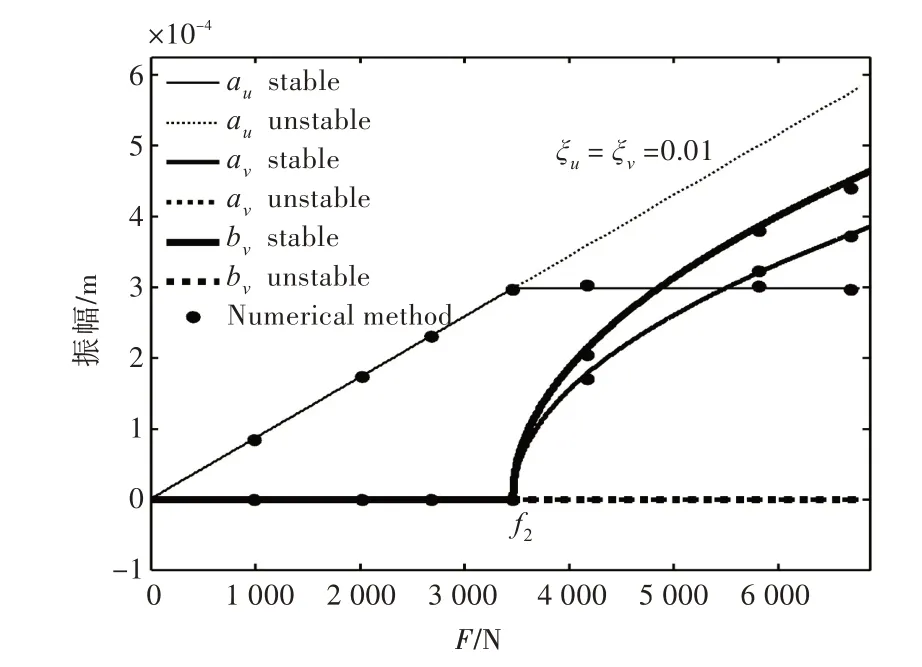
图5 纵向振动幅值、弯曲振动幅值随激励力的变化规律Fig.5 Variation of longitudinal vibration amplitude and bending vibration amplitude with excitation force

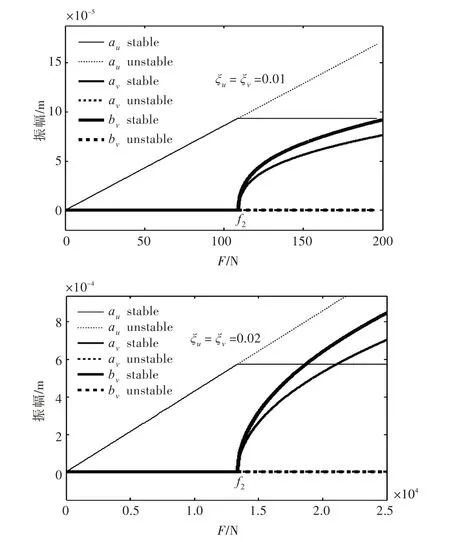
图6 临界载荷随阻尼比的变化规律Fig.6 Variation of critical load with damping ratio

3.4 轴系参数对系统非线性强弱程度的影响

本节将利用多尺度法探讨轴承刚度、螺旋桨质量及细长比等参数对非线性参数Λ1（反映轴系弯—纵耦合非线性强弱程度）的影响［23］，计算结果如图7 所示。从图中可以看出：在一定范围内增加后艉轴承刚度，可以抑制弯—纵耦合非线性效应；在一定范围内增加前艉轴承刚度和推力轴承刚度，可以增强弯—纵耦合非线性效应；中间轴承对弯—纵耦合效应的影响较小；增加螺旋桨质量、减少细长比也可以增强弯—纵耦合效应。

轴系参数对系统弯—纵耦合效应的影响机理具体如下：

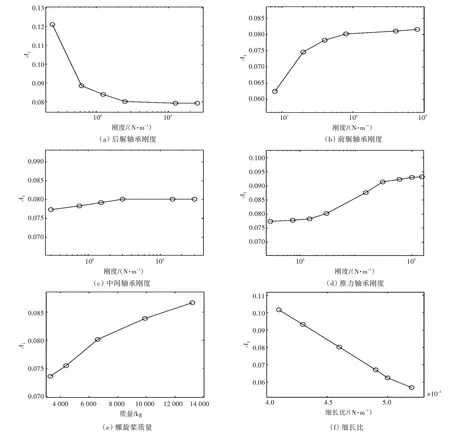
图7 轴系各参数对弯—纵耦合效应的影响Fig.7 Effect of the shaft parameters on the geometric nonlinear

1）推进轴系的第1 阶弯曲振动模态一般表现为螺旋桨处的振动。因此，增加后艉轴承刚度或减小螺旋桨质量可以有效减小轴系的弯曲振动，从而抑制轴系的弯—纵耦合效应。

2）对于轴系第1 阶纵向振动而言，由于推力轴承刚度一般远小于轴系自身的拉伸或压缩刚度，因此纵向第1 阶模态以轴系整体平移为主。这种振动模式不会使轴系产生纵向变形，所以也不会引起轴系的弯—纵耦合效应。然而，随着推力轴承刚度的增加，当其值与轴系自身的拉伸或压缩刚度相当时，轴系第1 阶纵向振动将不再表现为整体平移，而是轴系自身的纵向变形，此时轴系将产生明显的弯—纵耦合效应。同时，随着推力轴承刚度的增加，轴系弯—纵耦合效应越来越强。前艉轴承对第1 阶弯曲振动的影响规律与纵向振动相似，本文不再赘述。

3）由于中间轴承位于轴系前端，其对轴系第1阶弯曲振动模态的影响很小，故对系统弯—纵耦合效应的影响也不明显。

4）增加轴系的细长比可以有效增加轴系的刚度，从而减小轴系弯曲及纵向变形，最终抑制轴系的弯—纵耦合效应。

4 结 论

本文建立了轴系弯—纵耦合时的非线性振动偏微分方程，阐述了有限元法、多尺度法等非线性方程求解方法，分析了弯—纵耦合效应对轴系非线性振动特性的影响，得到如下结论：

1）与线性模型相比，弯—纵耦合效应将增加轴系的固有频率。

2）当轴系产生弯—纵耦合效应时，轴系振动响应中将出现多频响应、响应跳跃及能量迁移等复杂的振动现象。

3）增加后艉轴承刚度可以抑制轴系弯—纵耦合效应，增加前艉轴承刚度和推力轴承刚度可以增加轴系弯—纵耦合效应，而中间轴承对轴系弯—纵耦合效应的影响则较小。

4）激励载荷越大、阻尼比越小，轴系弯—纵耦合效应将越强。