基于文化算法的K均值聚类混合算法研究
2019-10-24贾丽丽
贾丽丽
聚类分析广泛应用于数据挖掘领域,许多专家学者已经提出了大量经典的和流行的聚类算法。传统聚类分析大致分五类,其中,基于划分聚类算法是算法研究中的一个热门的研究领域之一。而K均值法又是划分聚类分析算法中最经典的一类方案,能够归属到爬山法的范畴。该类算法具备的优势为原理实现简便,操作运行高效。只是该类算法也不可回避地存在极大的缺陷:第一,对于选定的初始值极其敏感。当其选用的初始值存在变化的时候,所得到的聚类结果也将呈现很大的差别;第二,局部极值的缺陷。该项算法是顺延能量递减的方向完成搜索操作,因此很容易深陷局部极值而难以获得最优解。
本文基于文化算法所具有的双层结构特性提出文化-K均值混合算法,该算法是把文化算法中知识空间(信仰空间)比较优的信息保留下,使其可以依靠保留优等经验的方式帮助更好地实现问题处理,实现全局寻优的功能目标,避免了对初始值选取敏感的问题,能有效地克服传统的K均值算法的两大缺点。因此,通过对文化算法的K均值聚类混合算法进行深入研究,呈现出良好的理论分析意义。
1 文化算法框架
通常,文化算法能够实现最新复杂度相对较高的全局寻优处理,其是一种基于知识的双层演化系统,包含两个演化空间:一层是通过群体之间的演化及其评价迭代搜索最优解,该空间由具体个体组成的群体空间(种群空间);另一层是在群体演化过程中经验知识组成的知识空间(信仰空间)。图1阐述了文化算法的基本框架[1]。
在图1 中,accept() 表征的是接受函数,influence()表征的是影响函数。在双层空间性质的通信协议构建期间,接受函数能够完成群体内选定个体相应经验知识的搜集整理,并且经由更新函数update()的支持实现信仰空间的调整处理;此时,影响函数能够依靠信仰空间内存在的各类知识经验,积极指引群体空间优化升级。
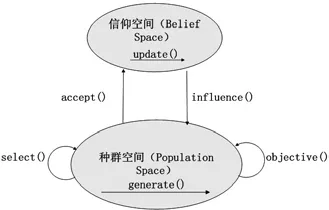
图1 文化算法基本框架
2 基于文化算法的K 均值聚类混合算法研究
2.1 K 均值聚类法
该聚类方法是实现聚类分析期间最经典的一种方法,具有原理简单、算法高效的优点。下面给出具体算法流程[2]:
Step2 随机选取K 个样本作为聚类中心并初始化;
Step3 计算各样本与各类中心的距离(采用欧式距离);
Step4 把各样本趋近到类中心点,运算获得各自的均值,充当最新的类中心;
Step5 判定:当类中心不呈现改变或是满足迭代次数,算法停止;反之,继续执行3。
2.2 基于文化算法的K 均值聚类混合算法
K均值聚类算法的两个缺点:一个是可能会导致不同的聚类结果,主要是由于初始值选取的敏感性;另一个是该算法很容易陷入局部优化,主要原因是该算法是沿着能量减少的方向搜索。这两个缺点,限制了该算法的范围。为了克服K均值聚类算法初始化敏感性和容易陷入局部优化两大缺点,引入文化算法加以改进,以文化算法为框架,K均值算法为聚类模型的混合聚类算法,针对聚类问题建立文化算法的双层空间进化模型,构建适合于聚类问题的信仰空间、种群空间、接受函数和影响函数,并运用各种知识加以指导,让问题可以在经验知识的指引下更好地实施求解分析,进而获得全局最优效果,在聚类中起到了良好的指导作用,从而具有较好的全局寻优性能,能够有效地克服K均值算法的两大缺点。适用于求解海量数据分析中的聚类问题。
2.2.1 文化-K 均值聚类混合算法框架

图2 文化-K均值聚类混合算法框架
2.2.2 种群空间(群体空间)的编码与适应度函数
在种群空间内,个体编码选定聚类中心内的实值编码充当,个体则选定K个聚类中心组建得到。如果d是模式向量维数,那么个体长度对应就是K×d实值码串。由文化算法是面向最小化问题,因此适应度函数采用类间误差平方和最小,即达到最小,d ij表示样本欧式距离。
2.2.3 信仰空间(知识空间)结构
信仰空间的结构采用文献[3]中的 〈S,N〉结构,即对应即为形势知识,属于最优个体构成的集合,m表征具备的最优个体及数量,表征第t代种群内对应着的第i个最优个体;表征规范知识,Xi表示为 〈I,L,U〉,n为变量数目。,初始化上限u和下限l经由样本具有的模式向量相关的下限以及上限得到;L j与Uj对应表征变量j所在的下限以及上限相关的适应值,经由初始化控制为+∞。
2.2.4 accept()接受函数
该函数能够实现会对现下信仰空间带来影响作用的知识经验个体相关的选择控制,并且种群空间内选定β比例完成最优个体的选择处理。
2.2.5 信仰空间的更新
在信仰空间实施的调整工作中,需要借以更新函数update()完成。其定义[4]情况是:选用最优个体实现知识空间内的更新处理,即,其中表示第 代最优个体。
规范知识N根据以下规则更新[5]:
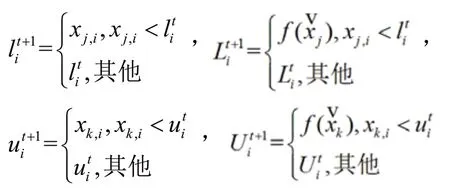
2.2.6 influence()影响函数
该类函数能够借由规范知识的方式对变量步长情况进行有效的调整控制,而借由形势知识实现变化方向的调整控制。相关定义[4]对应是:
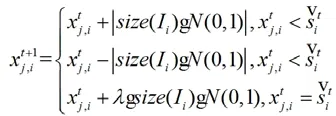
此处,N(01),对应表征满足标准正态分布要求的随机数,对应表征知识空间内变量i能够调整控制的区间长度,λ对应表征的是步长收缩因子情况。
2.3 算法实现步骤
Step1 种群空间初始化控制。随机选定K个样本充当分析的聚类中心,并实施编码;
Step2 经由适应度函数实现空间内相关个体的评价分析;
Step3 在已有待选解的基础上,参照知识空间结构获得相应的初始知识空间;
Step4 参照影响函数带给种群空间内各父代个体的变异影响,获得需要的p 个个体;
Step5 针对父子个体构建的2p 种群空间内的各个个体,随机选定c 个个体展开对比分析。若是该个体相较对比个体而言更优,则视其为胜利,并且把个体具备的胜利次数做好记录;
Step6 选定前p 个胜利次数最高的个体充当下代父体;
Step7 借助接受函数accept 实现信仰空间的更新处理;
Step8 若是与终止条件不相符,则继续Step4;否则,停止运行。
3 文化-K 均值聚类混合算法算例分析
算例[6]:给出2 个数据集。

表1 数据集说明
在数据集上实施五十次运算分析后,本文算法与初始K 均值算法的结果情况,参见表2。
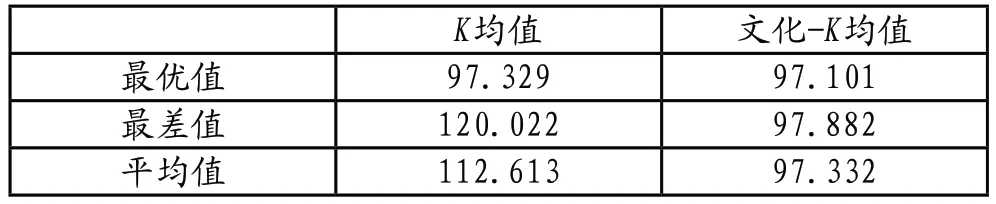
表2 两种算法在Iris数据集上比较
实验结果表明,K均值算法实现收敛的速度更快,只是更易出现局部最优的问题,而且会对选定的初始聚类中心更为敏感,而本文文化-K均值聚类混合算法的收敛速度虽慢一些,但能够获得全局最优值,且克服了初始聚类中心的敏感性。
