电池荷电状态估算方法研究

2019-10-24刘鹏飞

汽车文摘 2019年11期

关键词：端电压开路内阻

刘鹏飞

（南京普天大唐信息电子有限公司，南京 210000）

主题词：电池电路等效模型荷电状态（SOC） SOC估算

缩略语

SOC State Of Charge（荷电状态）

BMS Battery Management System（电池管理系统）

OCV Open Circuit Voltage（开路电压）

SEI Solid Electrolyte Interface（固体电解质界面膜）

PNGV Partnership for a New Generation of Vehicles

RC Resistance-Capacitance(电阻-电容)

GNLGeneral Nonlinear Model（非线性等效模型）

ACMAmphiphilic carbonaceous Material（两亲性炭材料）

KF Kalman Filtering（卡尔曼滤波）

EKF Extended Kalman Filter（扩展卡尔曼滤波法）

UKF Unscented Kalman Filter（无损卡尔曼滤波法）

HPSO Hybrid Particle Swarm Optimization（混合粒子群）

BP Back Propagation（神经网络）

PF Particle Filter（粒子滤波）

LMLevenberg-Marquardt（列文伯格-马奎特）

GA Genetic Algorithm（遗传算法）

ADAnalog-to-Digital（模拟量转数字量）

0 引言

在目前提倡低碳环保健康生活的发展形势下，以锂电池为动力的新能源汽车以环保、节能和轻便等优势正在取代燃油汽车的地位。其使用性能的优劣直接影响到汽车在市场的占有率。电池管理系统（Battery Management System，BMS）作为锂电池系统中的核心部件，能够提高锂电池的安全性和使用年限从而延长锂电池的使用年限[1]。准确估算锂电池荷电状态（State Of Charge，SOC）是BMS的基础[2]，其估算的准确性有利于BMS对电池的管理和均衡，关系到电池的充放电控制和电动汽车的优化管理[3]。而电池的SOC、电池的开路电压（Open Circuit Voltage，OCV）、电池端电压、充放电过程的电流值、电池温度和电池内阻等参数之间存在关系[4]，因此为了准确估算电池荷电状态，就需要确定电池荷电状态与上述参数之间的关系，所有需要建立以电压、电流、温度和内阻为主的电池等效模型，从而描述清楚电池的工作过程。本文介绍了目前主流的电池等效电路模型和估算SOC的方法。介绍了各自的原理，分析了各种估算方法间的优缺点，并总结出未来SOC估算的发展趋势，为新能源汽车发展提供参考。

1 SOC定义

电池荷电状态（SOC）是电池剩余容量与其充满状态时容量的比值，美国先进电池联合会在《电动汽车电池试验手册》中将SOC定义为：在环境温度为25℃的条件下，电池在一定的放电倍率下，剩余电量与相同条件下额定容量的比值[5]：

其中：Qs为电池剩余容量；Qz为电池额定容量。

2 电池等效电路模型

根据研究方向的区别，用于表征电池状态的模型也各不相同，可分为电池热模型、电学特性模型和电池老化模型[6]。通过建立电池热模型，可以用来预测电池工作过程中内部温度的变化过程[7]。现在学者在BERNARDI的生热速率模型[8]的基础上，研究了电池热量的来源[9]、电池内部热量的分布[10-11]、电池内部热量和电流密度分布[12]、电池组内部热量传导[13]等方面的内容，阐明了电池热量产生的机理以及温度分布，有助于设计合理的散热方式来保证电池正常工作。电学特性模型分为可分为黑箱模型、电化学机理模型和等效电路模型。黑箱模型利用神经网络模型[14]等新型模型结构，建立电池荷电状态（SOC）、电流、温度、内阻、开路电压以及电池端电压之间的模型，电化学机理模型以NEWMAN提出的多孔电极和浓溶液理论[15-16]来描述电池内部锂离子浓度和电化学反应变化。等效电路模型通过利用电阻、电容等元件来等效电池电化学反应过程，模型直观、易懂，结合多种算法可得到较高的准确性，因此具备较强的实用性。目前等效电路模型可分为Rint模型、Thevenin模型、PNGV模型、二阶RC模型和GNL模型[17]。电池老化模型主要研究固体电解质界面膜（Solid electrolyte interface，SEI）增长[18]和负极锂的沉积[19]对电池老化的影响，研究电池老化模型可开发出性能更优的电池材料、延长电池使用年限。

2.1 Rint模型

Rint模型[20]是将锂电池等效为理想电压源和电阻串联的模型，用理想电压源等效为电池的开路电压，用常值电阻来等效电池的欧姆电阻和极化电阻。该模型是理想化的模型，未考虑到温度、荷电状态、电池老化等外界参数对电池性能的影响，因此此模型多于理想状态下电池仿真，为高阶等效电路模型的建立提供理论依据，并不用于实际SOC的估算[21]。

2.2 Thevenin模型

Thevenin模型考虑到电池工作过程中的极化反应[22]，在Rint模型的基础上串联上由传荷阻抗Re和传荷电容Ce并联而成的RC回路[23]，如图1所示，其中Uoc是理想电压源，等效为电池的开路电压；Ro等效为电池的欧姆电阻，因此其端电压如式（2）所示：其中：U为电池端电压；UOC为电池开路电压；I()t为充放电电流；Ro为电池的等效欧姆电阻；Ue为电化学极化电压。

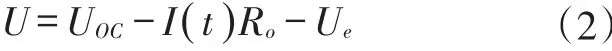
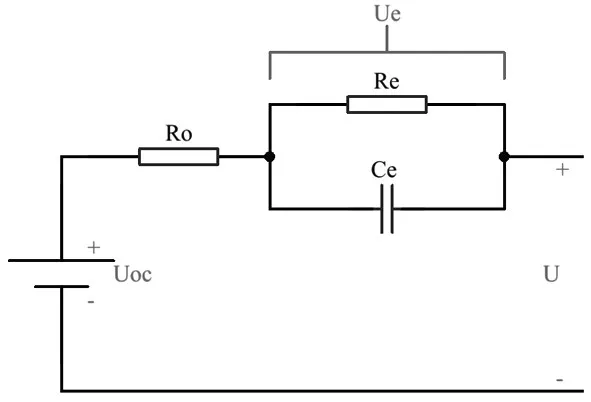
图1 Thevenin模型电路结构[23]

在Rint模型的基础上，Thevenin模型不仅考虑到电池工作过程中出现的欧姆极化，同时考虑到电化学极化过程。Thevenin模型结构简单，元器件具有物理意义，在电池不发生较大变化时，可较为准确的反应出锂电池在充放电过程中的变化情况。但是随着电池温度、电池充放电循环次数的增加、充放电电流等外界因素的变化，模型中电阻值也会发生相应变化，导致模型的仿真精度下降。

2.3PNGV模型

PNGV模型最早由Johnson在《PNGV电池试验手册》[24]中提出，考虑到电池的开路电压随电流的时间累积的差异，PNGV模型在Thevenin模型的基础上串联了储能电容Cq用来表征电池开路电压的变化情况。如图2所示，Uoc是等效为电池的开路电压；Ro等效为电池的欧姆电阻，Re为传荷阻抗，Ce为传荷电容，因此其端电压如式（3）所示：

其中：U为电池端电压；UOC为电池开路电压为充放电电流；Ro为电池的等效欧姆电阻；Ue为电化学极化电压；Uq为储能电容Cq两端电压。

PNGV模型利用储能电容Cq来表征电池开路电压随电流时间积分的差异，因此PNGV模型比Thevenin模型具有更高的精确度和动态特性，能更好描述电池充放电过程，但是长时间的充放电过程会在储能电容Cq累积误差，从而削减了模型的精确度。

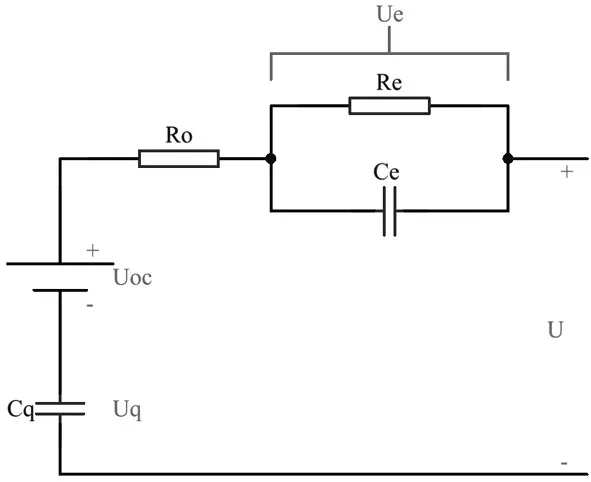
图2 PNGV模型电路结构[24]

2.4 二阶RC模型

二阶RC模型[25]是在Thevenin模型的基础上改进而来的，二阶RC模型将电池极化反应分为了电化学极化与浓差极化，因此二阶RC模型在Thevenin模型电路上串联了个用来描述电池浓差极化的RC并联电路。如图3所示，其中Uoc是等效为电池的开路电压；Ro等效为电池的欧姆电阻，Re为传荷阻抗，Ce为传荷电容，Rc为浓差阻抗，Cc为浓差电容，因此其端电压如式（4）所示：

其中：U为电池端电压；UOC为电池开路电压为充放电电流；Ro为电池的等效欧姆电阻；Ue为电化学极化电压；Uc为浓差极化电压。

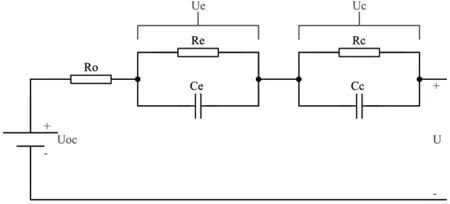
图3 二阶RC模型电路结构[25]

虽然较Rint模型、Thevenin模型而言，二阶RC模型电路结构较为复杂，但是二阶RC模型同时考虑到电池工作过程中出现的欧姆极化、电化学极化和浓差极化现象，也接近电池的实际工作过程，精度更高，且随着芯片计算功能的提高，二阶RC模型被广泛用于实际SOC估算中。

2.5GNL模型

GNL模型[26]在二阶RC模型的基础上做出了进一步的优化，电路结构如图4所示，Uoc是等效为电池的开路电压；Ro等效为电池的欧姆电阻，Re为传荷阻抗，Ce为传荷电容，Rc为浓差阻抗，Cc为浓差电容，Rs为电池的自放电电阻，用来描述电场自放电对电池端电压的影响，因此其端电压如式（5）所示：

其中：U为电池端电压；UOC为电池开路电压；为充放电电流；Ro为电池的等效欧姆电阻；Ue为电化学极化电压；Uq为储能电容Cq两端电压；Uc为浓差极化电压。

图4 GNL模型电路结构[26]

GNL模型继承了上述4种电池等效电路模型的优点，考虑到电池工作过程中各种因素对电池端电压的影响，因此GNL模型最为接近电池内部特性，因此GNL模型广泛应用于电池理论分析领域，但是GNL模型阶次较高且模型中参数辨识过程较为繁琐，所以GNL模型并不适用于实际SOC估算中。

3 SOC估算方法

3.1 传统SOC估算方法

3.1.1 放电法

放电法是公认的较为可靠的估算SOC的方法，适用于所有锂电池。放电法是指对锂电池以恒定不变的电流进行长时间的放电，直至将电池放空，放电时间和放电电流的乘积即为电池的放电容量。但该方法一般用于电池容量的标定，测量过程需要离线测试。

3.1.2 开路电压法

开路电压法是将电池长时间静置，使其处于既不放电也不充电的状态，当电池端电压不在发生波动时，即为所需的开路电压，根据建立的开路电压和SOC关系曲线，通过查询曲线得到当前开路电压所对应的SOC。文献[27]通过对车用ACM电池在不同环境温度下荷电状态与开路电压的关系研究，发现ACM电池在其规定的工作温度范围内，其SOC与OCV有着良好的线性关系。

但是直接使用开路电压法测量电池的荷电状态时通常需要将电池搁置2 h以上，因此会在测量开路电压上耗费较多时间。文献[28-31]采用等效电池模型，通过对电池充放电过程进行试验，找到充放电过程中电池端电压与电池开路电压中间的关系，利用电池端电压来表征电池的开路电压，从而来估算电池SOC，以此解决开路电压法中需要长时间静置电池的弊端。但是当电池剩余容量为额定容量的30%到80%时，锂电池的开路电压基本保持不变，这意味着较小的电压变化会引起较大的SOC误差，要追求高精度的SOC估算，对电压采样电路精度提出较高的要求[32-33]。

3.1.3 安时积分法

安时积分法[34-35]是利用电池流入流出的电流对时间的积分，计算出电池的输入输出电量。安时积分法只与充放电过程中电流值有关，易于实现实时监测，适用于各种电池。安时积分法计算公式如下[36]：

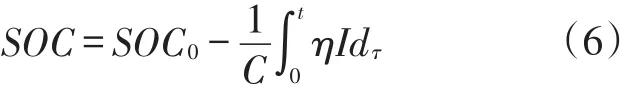
其中：SOC0为电池的初始容量；C为电池的额定容量；I为电池电池，其正负与电池所处状态有关；η为库仑效率系数。

因此，电池的初始容量的正确性直接影响到SOC估算结果，因此现有学者[37-38]多采用开路电压法来估算电池的初始容量，结合安时积分法来估算SOC。电流采样的误差会导致SOC的估算误差，因此往往选用采用精度高的电流传感来提高电流的采样精度，但此措施会额外增加系统的成本不易于推广。学术界在此方法基础上提出了改进措施，文献[39]研究了普通传感器在估算镍氢电池SOC时产生的误差，修正了电流传感器模型，结果表明，利用修正后电池传感器模型估算电池荷电状态产生的误差远小于修正前的误差。文献[40]考虑到温度、放电电流、充放电次数等因素对SOC估算的影响，提出了一种改进的安时积分法：

式中，α为自放电及老化因素的修正因子；δ为电池总容量C的修正因子。

3.1.4 内阻法

和开路电压法一样，内阻法也是通过大量的试验测量得到电池的SOC和内阻的曲线图，SOC的精度，测量时需要将测试电路与电池可靠连接，以减少接触电阻对SOC估算的影响。直流内阻测试结果不受充电器纹波和噪声的影响，测量可控制在0.1%之内，但电流过大、时间过长时，电池会出现极化内阻从而增大测量误差[41]。文献[42]改进了传统内阻法，对SOC和内阻变化量ΔR进行建模，结果表明该经验公式可运用于不同型号的、健康状况良好的蓄电池SOC测量，测量误差可控制在10%以内。交流内阻法是在电池两端加上特定频率的交流信号，根据测量所得的参数，计算出此时电阻的内阻[43-44]。

3.2 新型SOC估算方法

3.2.1 卡尔曼滤波法

卡尔曼滤波法（Kalman Filtering，KF）采用了噪声与信号的状态空间模型。利用前一时刻的估计值和当前时刻的观测值来更新对状态变量的估计[45]。估算SOC时，将充放电过程中电流值作为输入，电池端电压作为输出，以电池电压的实测值和SOC估算值的误差更新系统的状态，直至方差最小，得到SOC估算值[46]。该方法的实质是用测量所得的电压值修正安时积分法得到SOC估算值，其计算方法为[47]：

其中：S为状态变量SOC；I为电流；V为电压；ηi为电流效率；Ci为电池额定容量；Δt为时间间隔；wk和vk为互不相关的零均值高斯白噪声。

目前，卡尔曼滤波算法分为标准卡尔曼滤波法（KF）、扩展卡尔曼滤波法（EKF）和无损卡尔曼滤波法（UKF）。文献[48]比较了KF和EKF估算电池荷电状态的实验结果，实验表明：KF不能降低非线性信号处理存在的误差，而EKF在估算SOC时能够将误差控制在5%以内。文献[49]在EKF的基础上，提出了基于模糊控制的EKF的SOC估算法，其可以提高SOC估计精度、减小估算误差。文献[50]以电池复合模型为基础，应用递推最小二乘法辨识电池参数，利用改进型UKF算法对电池SOC进行估计，改进型UKF算法具有很好的鲁棒性和跟踪速度，各类误差精度均控制在5%以内。针对UKF在估计电池荷电状态中存在收敛速度较慢、容易发散等问题，增加了自适应调节因子和衰减因子，该算法估算SOC值误差精度可小于1%，在估计精度及收敛速度上均优于UKF[51]。

KF克服了安时积分法中SOC估算误差受SOC初始值影响较大的缺点，且对初始值的精度要求较低，但是其估算值较大程度上依赖建立的电池模型的准确性。

3.2.2 BP神经网络法

神经网络法[46]通过调整建立的模型中权重和偏差的方法提高模型的精度。利用BP神经网络法对电池SOC进行估算，以学习后的网络作为数学模型，其中输入层为电池端电压、充放电电流值、电池温度和电池内阻；隐含层为系统的激活函数；输出层为电池的SOC估算值。

图5 BP神经网络结构图[46]

文献[52]以动力电池的电压、电流、温度和内阻作为输入，SOC作为输出，建立4输入1输出的神经网络仿真模型，SOC的预测度为1.6%，比未考虑电池内阻的预测精度提高45%左右。文献[53]在BP神经网络法的基础上采用将混合粒子群（HPSO）结合BP神经网络的算法，通过优化神经网络的初始值和阈值克服了种群易陷入局部极小的缺点，加快了收敛速度，减小了SOC预估的误差。

神经网络法不需要建立电池的数学模型，适用于所有电池，估算速度快、精度高。但是BP算法需要训练模型，其训练数据、训练方法对SOC估算结果有较大影响。

3.2.3 粒子滤波法

粒子滤波（Particle Filter，PF）通过寻找状态空间的随机样本来近似表示概率密度函数，以样本均值代替积分运算，PF也是获得系统状态的最小方差估计的过程。利用粒子滤波估算锂电池的SOC的具体计算步骤如下[54]：

状态空间模型中，锂电池SOC和锂电池负载电压分别为状态变量和观测变量。

其中：wk为系统过程噪声，vk为系统观测噪声，Δt为系统采样周期。

（1）初始化：k=0

p(x0)随机产生N个粒子

（2）状态预测

（3）粒子权重计算和归一化

当系统获得新的观测值yk，通过观测方程获得新的预测值的误差计算粒子的权重wi：

归一化处理：

（4）重采样

基于生成的新的随机样本分布，通过重采样复制高概率的粒子，淘汰低概率粒子形成新的样本分布。重采样后的粒子权重均为1/N。输出估计值

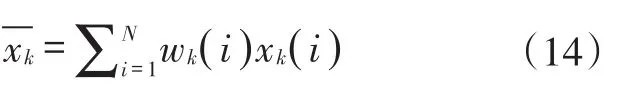
循环迭代重复步骤（2）到（4），实现状态量xk的递推估计。

3.3 其他新方法

近年来学者提出了新的估算SOC的方法，比如基于灰色多变量模型[55]、免疫遗传算法和BP神经网络相结合[56]、模糊控制法[57]、自适应法和列文伯格-马奎特算法（Levenberg-Marquardt,LM）结合优化BP神经网络[58]、遗传算法（Genetic Algorithm，GA）结合BP神经网络[59]、随机森林回归算法[60]、支持向量机[61]等等。这些算法中大多数都是对上述传统和新型SOC估算方法中出现的误差进行修正来提高估算精度。