基于EXCEL的某轻型客车前悬架K特性分析

刘鹏坤， 李明安

(潍柴动力股份有限公司 上海研发中心客车所， 上海 201114)

汽车的操纵稳定性是汽车安全行驶的主要性能，是“车辆高速行驶的生命线”[1]。而悬架是操纵稳定性的灵魂，故悬架K/C特性的研究对于提高整车性能至关重要。通过EXCEL对前悬架运动建模分析可直观了解前悬架运动状况及K特性，且可节省通过ADAMS/Car多体运动学分析软件进行分析的时间。

1 前悬架结构及运动学模型建立

1—转向机； 2—副车架； 3—转向拉杆； 4—下摆臂；5—减振器； 6—转向节。图1 横置板簧式麦弗逊前悬架

以图1所示的横置板簧式麦弗逊前悬架的结构型式为例进行研究。图中下摆臂4内侧通过螺栓与副车架2铰接在一起，下摆臂4外侧与转向节6下部通过球销相连，转向节6上部与滑动立柱固定，并沿减振器5的活塞杆上下滑动。转向拉杆3外侧与转向节6通过球销相连，内侧与转向机1通过球销相连[2]。

依据图1前悬架结构形式，建立如图2所示的前悬架刚体运动学模型。

A—减振器上点； B—减振器下点； C—下摆臂外点；D、E—下摆臂旋转轴线端点； F—转向拉杆外球销点；G—转向拉杆内球销点； H—车轮中心点；K—车轮轴线内点； I—转向机轴线内点； L—车轮接地点。图2 麦弗逊前悬架刚体运动学模型

下摆臂CDE沿轴线DE上下摆动，转向拉杆内点G沿着转向机轴线IG左右运动，转向节BCF沿着轴线AB进行上下滑动。点A、C、F、G均为球销连接。假设车轮为刚性，H、K、L固结在转向节BCF上。AC为虚拟主销轴线[3-4]。

2 前悬架K特性分析及验证

2.1 输入数据

首先确定各个关键点在整车坐标系中的初始坐标位置及整车参数。某轻型客车整车参数为：车辆轴距3 665 mm,前轴轮距1 710 mm；轮胎自由半径376 mm，静力半径347 mm。前悬架关键位置点见表1。

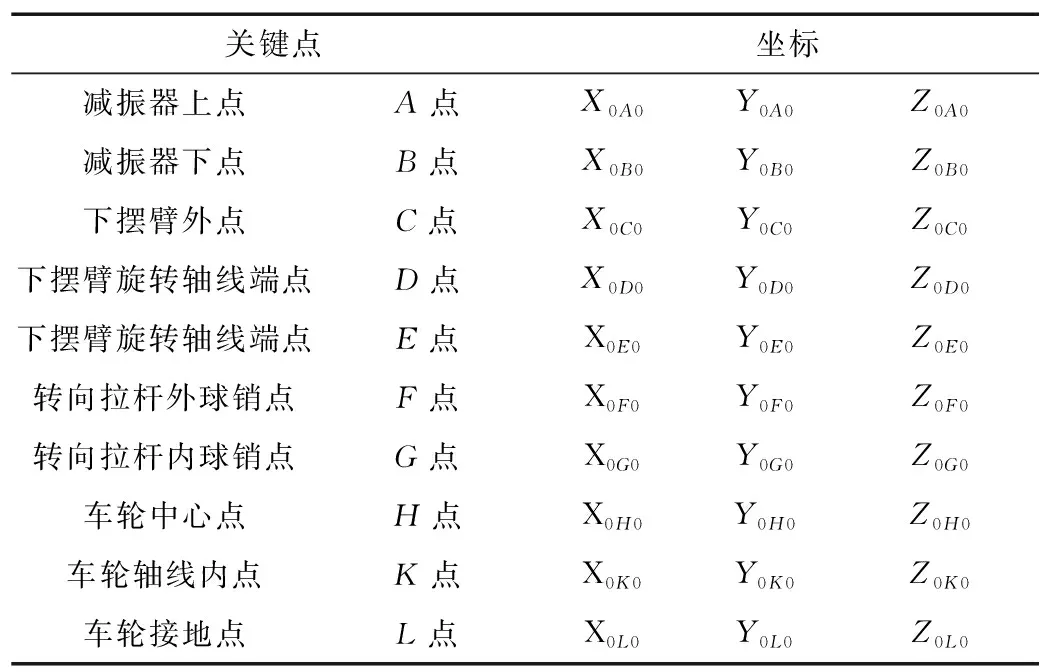
表1 关键点坐标 mm

2.2 坐标转换

2.2.1C点整车坐标

整车坐标系X0Y0Y0符合右手定则，原点在整车纵向平面上，X正方向指向后侧，Y正方向指向车右侧，Z正方向垂直向上。假设外摆臂旋转θ角，M点为C点到旋转轴线DE的垂足，则C点坐标为：

X0Cθ=X0M
Y0Cθ=Y0M-LC-DE·cos(θ0-θ)
Z0Cθ=Z0M-LC-DE·sin(θ0-θ)

式中：LC-DE为C点到旋转轴线DE的距离。

则主销内倾角α为：

αθ=arctan [(Y0A0-Y0Cθ)/(Z0A0-Z0Cθ)]

(1)

主销外倾角τ为：

τθ=arctan[(X0A0-X0Cθ)/(Z0A0-Z0Cθ)]

(2)

2.2.2F点整车坐标

图3为A点主销坐标系及其变换角度。坐标系X1Y1Z1原点在A点，平行于整车坐标系X0Y0Z0，A点整车坐标为(X0A,Y0A,Z0A)，坐标系X2Y2Z2由坐标系X1Y1Z1绕X1轴旋转α角得到，主销坐标系XAYAZA由坐标系X2Y2Z2绕Y2轴旋转β角得到。则主销坐标系XAYAZA与整车坐标系转换矩阵为：

[X0Y0Z01]=[XAYAZA1]T1

(3)

式中：

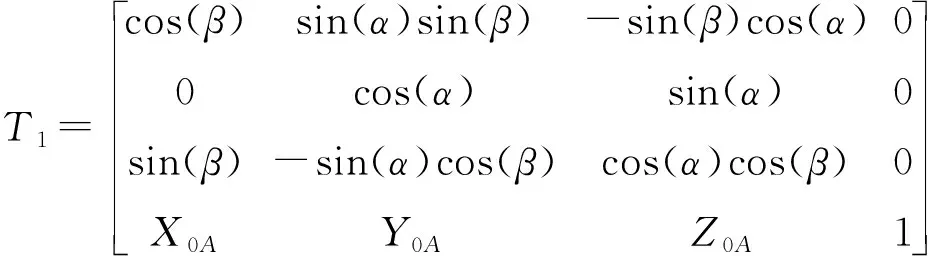
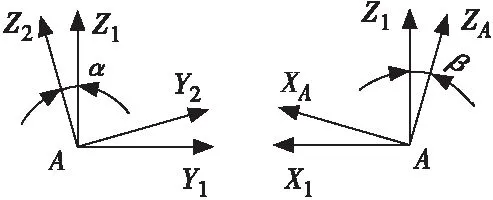
图3 A点主销坐标系及其变换角度

图4为AFC面主销坐标系及其变换角度。坐标系X3Y3Z3原点在A点，由主销坐标系XAYAZA绕ZA轴旋转γ角得到，轴Y3垂直于平面ACF。坐标系X4Y4Z4由主销坐标系X3Y3Z3绕Y3轴旋转δ角得到, 轴Z3与直线AC重合。则主销坐标系XAYAZA与坐标系X4Y4Z4转换矩阵为[5-8]：

[XAYAZA1]=[X4Y4Z41]T2

(4)

式中：

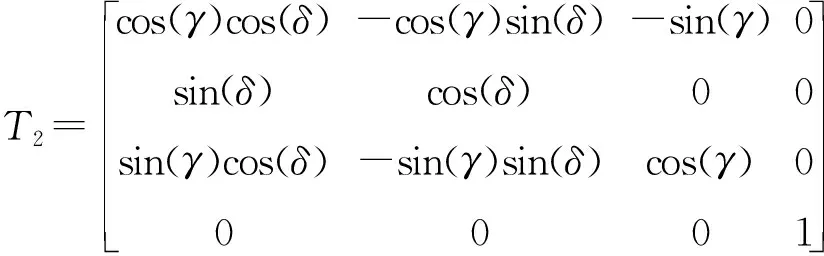
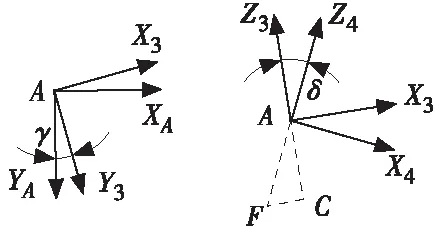
图4 AFC面主销坐标系及其变换角度

将F点在坐标系X4Y4Z4中的坐标、G点在整车坐标系中的坐标均转化为主销坐标系XAYAZA中的坐标：

[XAFθYAFθZAFθ1]=[X4FθY4FθZ4Fθ1]T2

(5)

[XAGθYAGθZAGθ1]=[X0GθY0GθZ0Gθ1]T1-1

(6)

(7)

联立式(5)、式(6)、式(7)可求得γθ值。则任意时刻F点整车坐标为：

[X0FθY0FθZ0Fθ1]=[X4F0Y4F0Z4F01]T2T1

(8)

2.2.3B点整车坐标

坐标系X5Y5Z5原点在A点，由主销坐标系XAYAZA绕ZA轴旋转ρ角度得到，使X5轴垂直于平面ABC。则坐标系X5Y5Z5与主销坐标系XAYAZA之间转换关系为：

式中:

(9)

B点在坐标系X5Y5Z5中任意时刻的坐标为：

X5Bθ=0
Y5Bθ=LABθ·sin(ζθ)

(10)

Z5Bθ=-LABθ·cos(ζθ)

F点在坐标系X5Y5Z5中任意时刻的坐标为：

(11)

又有：

(12)

联立式(10)、式(11)、式(12)可求得ρθ值。则任意时刻B点的整车坐标为：

(13)

2.2.4H、K、L点整车坐标

图5 转向节坐标系及其变换角度

图5为转向节坐标系及其变换角度。坐标系X6Y6Z6原点在C点，平行于整车坐标系X0Y0Z0，C点整车坐标为(X0Cθ,Y0Cθ,Z0Cθ)。坐标系X7Y7Z7由坐标系X6Y6Z6绕Z5轴旋转φ角得到，φ角为直线CF在水平面的投影与X5轴的夹角。坐标系X8Y8Z8由坐标系X7Y7Z7绕Y7轴旋转ξ角得到，ξ角为直线CF与平面X5Y5之间的夹角。此时坐标轴X7与直线CF相重合。转向节坐标系XCYCZC由坐标系X8Y8Z8绕X8轴旋转ψ角得到，使YC轴垂直于平面BCF。假设车轮为刚体且无绕车轮中心线的旋转运动，则B、C、H、K、L5点为转向节刚体上的固定点。悬架运动过程中，该点相对于转向节坐标系XCYCZC坐标值固定不变。由上述坐标系变换分析得：

(14)

(15)

其中：

(16)

(17)

将B点整车坐标带入式(14)，联立式(15)，且由于YC轴垂直于平面BCF，则任意时刻YCBθ=0，可联立求得ψ：

(18)

(19)

已知H、K、L点初始整车坐标，则任意时刻H、K、L点在转向节坐标系XCYCZC上的坐标为：

将任意时刻H、K、L点在转向节坐标系XCYCZC上的坐标带入式(18)可得H、K、L点整车坐标为：

则车轮外倾角μ为：

μθ=arctan[(Z0Kθ-Z0Hθ)/(Y0Kθ-Y0Hθ)]

(20)

车轮前束角ν为：

νθ=arctan[(X0Kθ-X0Hθ)/(Y0Kθ-Y0Hθ)]

(21)

轮距Lθ:

Lθ=-2·Y0Lθ

(22)

轮心跳动Hθ:

Hθ=Z0Hθ-Z0H0

(23)

2.3 平行轮跳计算分析

悬架的K特性参数主要包括静态前束角、静态外倾角、主销后倾角、主销内倾角、前束变化、悬架偏频等。通常通过双轮平行跳动来模拟汽车加减速、过减速带等障碍物及路面不平引起的颠簸运动对悬架K特性参数的影响。本文即通过双轮平行跳动仿真来分析主销内倾角、主销后倾角、车轮外倾角、车轮前束角、车轮轮距随车轮跳动的变化[9-10]。

通过上述2.2计算公式，设置θ角范围为(-15°～15°)，间隔为0.1°，利用EXCEL对悬架系统进行300个位置点坐标转换计算，得出悬架平行轮跳试验结果。具体结果如图6和图7中的“计算值”所示。

图6 车轮定位角对比

图7 车轮轮距对比

2.4 对比分析验证

通过ADAMS/Car建立横置板簧式前悬架运动模型，如图8所示(横置板簧式弹簧力利用螺旋弹簧模拟)。对前悬架进行平行轮跳试验[11-12]，具体结果如图6和图7中的“试验值”所示。

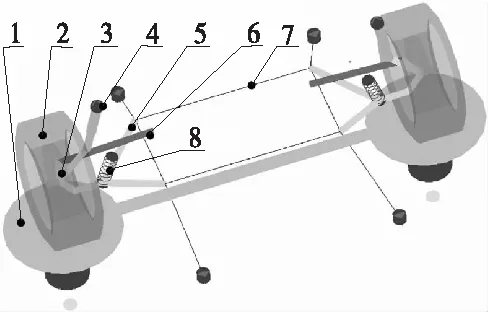
1—试验台； 2—车轮； 3—转向节； 4—减振器； 5—下摆臂；6—转向拉杆； 7—副车架； 8—螺旋弹簧。图8 横置板簧独立悬架ADAMS模型

由图6和图7的结果对比可知，计算所得的前悬架K特性与ADAMS/Car仿真所得结果基本一致(差别小于0.5%)。故可通过坐标转换计算悬架K特性，提前预测悬架K特性，为汽车设计提供参考。

3 结束语

利用EXCEL，通过坐标旋转变换得到的前悬架平行轮跳计算结果与ADAMS/Car仿真结果完全一致，在某些情况下，可利用该方法代替ADAMS/Car仿真，减少CAE分析工作量。悬架运动是多工况、多系统相互作用的综合结果，后续工作需要分析研究各硬点位置的优化及悬架C特性问题。