考虑紧急度的救灾车辆路径问题建模与优化

张玉州 徐廷政 郑军帅 饶舜

摘 要：为了减少救灾物资配送的延误时间和救灾车辆的总运输时间，引入紧急度的概念，建立了基于紧急度的救灾物资车辆路径问题模型，并设计了一种改进遗传算法对该模型进行求解。首先，采用多种策略生成初始种群;然后，提出一种基于紧急度的任务再分配算法作为局部搜索算子，该算法依据紧急度为延误安置点重新安排配送车辆或调整配送顺序从而减少延误时间，对无延误的车辆优化其路线从而减少总运输时间，以达到延误时间和总运输时间两者最优。在17个数据集上与先来先服务（FCFS）算法、按紧急度排序（URGS）算法和遗传算法（GA）三种算法进行了对比。实验结果表明，具有基于紧急度的任务再分配策略的遗传算法（TRUD-GA）与GA相比，平均延误时间减少25.0%，平均运输时间减少1.9%，与FCFS、URGS算法相比改进则更加明显。

关键词：紧急度;优化;车辆路径问题;遗传算法;局部搜索

中图分类号： TP301.6

文献标志码：A

Modeling and optimization of disaster relief vehicle routing problem considering urgency

ZHANG Yuzhou1，2， XU Tingzheng1，2*， ZHENG Junshuai1，2， RAO Shun1，2

1.School of Computer and Information， Anqing Normal University， Anqing Anhui 246133， China ;

2.Key Laboratory of Intelligent Perception and Computing in Anhui Province， Anqing Anhui 246011， China

Abstract： In order to reduce the delay time of disaster relief materials distribution and the total transportation time of disaster relief vehicles， the concept of urgency was introduced to establish a vehicle routing problem model of disaster relief vehicles based on urgency， and an improved Genetic Algorithm （GA） was designed to solve the model. Firstly， multiple strategies were used to generate the initial population. Then， an urgency-based task redistribution algorithm was proposed as local search operator. The proposed algorithm achieved the optimal delay time and total transportation time based on urgency. The delay time was reduced by rescheduling the vehicle or adjusting the delivery sequence for delay placements. The routes of the vehicles without delay were optimized to reduce the total transportation time. In the experiments， the proposed algorithm was compared with First-Come-First-Served （FCFS） algorithm， Sort by URGency （URGS） and GA on 17 datasets. Results show that the Genetic Algorithm with Task Redistribution strategy based on Urgency Degree （TRUD-GA） reduces the average delay time by 25.0% and decreases the average transportation time by 1.9% compared with GA， and has more obvious improvement compared with FCFS and URGS algorithms.

Key words： urgency; optimization; Vehicle Routing Problem （VRP）; Genetic Algorithm （GA）; local search

0 引言

我國是世界范围内自然灾害最严重的国家之一，发生灾害种类多、频率高，造成的人民生命财产损失巨大。灾害发生后的72小时被称为“72小时黄金救援期”，说明了救灾工作的紧迫性，因此，最大限度节省救灾物资配送时间具有重要的现实意义。应急物流路径规划已经成为一个研究热点[1-5]。

目前，国内外学者在救灾物资配送路径规划方面进行了相关研究。如根据应急救灾中的物资需求和道路通行时间等信息动态更新的情况，对车辆行驶路径动态规划进行求解[6-9]。Zheng等[10]针对路况信息不确定的情况，采取模糊的方法求解。在实际生活中的确存在路况不确定情况，而使用模糊求解方式能大幅减小不确定因素的干扰，效果较好。易云飞等[11]讨论了物流配送中考虑用户满意度、需求动态改变的多目标车辆路径问题模型的建立和优化，并设计伊藤算法结合蚁群算法等进行多目标优化求解。这种模型适用于一些不紧急的应用场景，如超市供货、快递员取件等。任锡德等[12]考虑受灾点物资配送的路径长度均衡性和总时间两个目标，这种优化目标可使送货车队的各车工作量较为均衡，重点主要是在送货方角度考虑问题。文仁强等[13]考虑了多供应点、多种物资类型的情况，提出了多物资点为多个资源需求点协同配送物资的多目标优化模型，其优势在于将问题情况细化，加入了多物资类型和多供应点要素。徐志宇等[14]以供需差异最小化、配送时间最短化、各灾点失衡度最低化为目标。朱建明等[15]以未满足的需求量和总的物资延误时间最小为目标。

综上，目前应急救灾车辆路径问题的研究常见多种因素综合考虑，如：总运输时间与受灾点失衡度、信息不确定性与客户满意度等。虽然在考虑求解目标上具有一定广度，但缺乏对“救灾时效性”这一目标的研究深度。从灾民的角度看，必然希望第一时间得到救助，因此要尽可能地提高救灾时效性。提高时效性就需要综合考虑总延误时间与总运输时间，只考虑总时间可能会为了整体时间的减少而牺牲掉某一个安置点的及时配送;以延误时间为单一优化目标的算法则可能导致总体运输时间的增加，推迟了每个安置点获得物资的时间，导致灾民的风险增大。

为提高救灾的及时性，降低运输风险，本文从救灾实际出发，提出了总运输时间和总延误时间双目标的优化模型，并设计了一种遗传算法（Genetic Algorithm， GA）对问题进行求解，其中包括一种局部搜索算法，即基于紧急度的任务再分配（Task Reassignment with Urgency Degree，TRUD）算子，同时在生成初始解阶段采用多种优化策略生成，以提高初始种群的质量。经过仿真实验的验证，本文模型及求解算法在保证延误时间最小化的同时缩短了总运输路径长度，与一些经典算法对比优势明显。

1 问题分析与建模

1.1 问题描述

灾害发生后，受灾群众被安置在n个临时安置点，每个安置点需要救灾物资的数量和需求的急迫程度不同。为了使问题更易于求解，引入紧急度的概念，其数值为某个安置点的截止时间和救灾车队出发时间所相差的分钟数。假设当前时间为8：00，救灾车队即将出发。甲村情况非常紧急，要求3h内获得50单位物资;乙村形势相对缓和，要求8h获得100单位物资。此时称甲村紧急度为180，截止时间为11：00;乙村紧急度为480，截止时间为14：00。在配送救灾物资时，将以紧急度作为确定安置点配送顺序和路径改进的重要依据。救灾车队必须尽最大可能减少物资配送到各安置点的延误时间，最小化车队总行驶时间，即同时优化总延误时间和总运输时间两目标。

1.2 问题建模

1.2.1 模型设计与约定

应急救灾的物流路径规划问题可以抽象为车辆路径问题（Vehicle Routing Problem， VRP）。灾民分布在n个安置点，各安置点的物资需求量为qi， m辆车从物资储备仓库（Depot）出发，各自配送一定数量的安置点，n个安置点全部配送完成后车辆空载返回，此过程形成m条回路。根据实际情况设置下列规定和限制条件：

1）所有运输车辆的容量和速度相同;

2）各安置点之间均有通路;

3）每个安置点只配送一次;

4）各安置点需求量已知;

5）各安置点截止时间已知;

6）每个安置点配送一次且仅配送一次完成;

7）各安置点对物资的需求量用若干个单位数量的物资表示;

8）任一运输车配送路线上各安置点的合计需求量不能超过该运输车的容量;

9）各安置点根据其紧急的程度上报截止时间，越紧急其截止时间越提前。

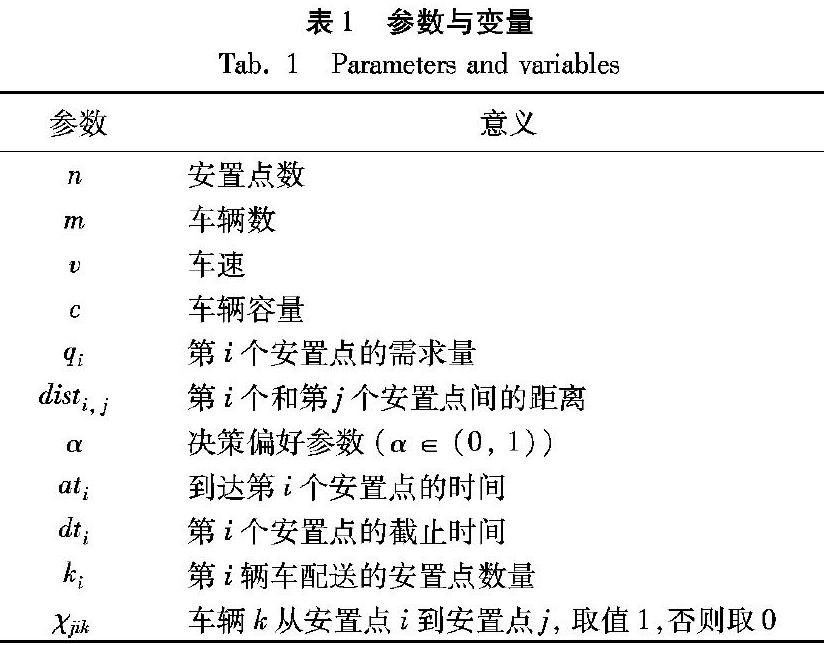
1.2.2 参数与变量

本文所用参数与变量如表1所示。

1.2.3 数学模型

根据以上假设和定义，结合VRP模型，建立如下应急救灾车辆路径问题的数学模型及目标函数。

min Z=∑ n i=0 ∑ n j=0 ∑ m k=1 disti，j·χijk

（1）

s.t.

∑ n j=1 χijk=∑ n j=1 χjik≤1; k∈{1，2，…，m}

（2）

∑ n j=0 ∑ m k=1 χijk=1; i∈{1，2，…，n}

（3）

∑ n i=1 ∑ n j=1 qi·χijk≤c; k∈{1，2，…，m}

（4）

min z1=∑ m i=1 ∑ ki j=1 （atj-dtj）

（5）

min z2= 1 v  ∑ m i=1 ∑ ki j=0 distj， j+1

（6）

min z3=  1-α v  ∑ m i=1 ∑ ki j=0 distj， j+1+α∑ m i=1 ∑ ki j=1 （atj-dtj）

（7）

上述建立的數学模型中：式（1）为基本VRP模型的目标函数，一般为车辆运输距离的总里程;式（2）确保车辆总路线是闭合型的，从某点出发并最终返回该点;式（3）表示每个客户有且只有一辆车对其进行服务;式（4）表示每辆车不得超载;式（5）表示车队总的配送延误时间;

式（6）表示车队总运输时间，且式中0以及ki+1（当j=ki时， j+1=ki+1）都代表物资储备仓库;

式（7）表示两目标协同优化，通过系数α调节总运输时间和总延误时间的权重，以确定算法优化的方向偏好，在0到1之间，α取值越大，函数越偏向于优化延误时间，反之偏向于优化总运输时间。

2 引入紧急度概念的改进遗传算法

遗传算法是一种有代表性的元启发式算法，具有良好的鲁棒性和扩展性，广泛应用于复杂组合优化问题的求解。遗传算法在VRP解空间中选取若干个解组成一个集合，这些解称为个体，即染色体，该集合称为种群。根据达尔文进化论的思想，在种群内部选择优秀个体，进行染色体交叉、变异等操作，经过n次迭代优化，求得最优解。本文在传统遗传算法的基础上改进了其初始解生成策略，提高了前期收敛速度，同时根据问题特性，提出了一种局部搜索算子TRUD，增强其局部搜索能力，在出现延误点时还具有定向搜索能力，避免陷入局部最优解和早熟。

2.1 染色体编码

1）给每个安置点分配一个序号，生成一个包含所有安置点的序列。

2）将安置点逐个分配给某辆车，直至达到容量限制;剩下的安置点继续分配给下一辆车，直至所有安置点都分配完成。

2.2 适应度函数

本文中的一条染色体包含m条回路，适应度函数的目标是

总运输时间和总延误时间的协同优化。α表示决策偏好参数，取值在0到1之间：取值越大，物资延误时间所占的权重越大，则越不能容忍延误情况的发生;若α取较小值，则意味着在减少安置点平均等待时间的前提下，可以容忍少量延误。适应度函数如式 （7）。由于本文的目标是时间的最小化，所以适应度函数是极小化的，其函数值越小表示适应度越高。

2.3 局部搜索算子TRUD

对于传统VRP，由于适应度评价对象是一整条基因序列，而对单个基因位不能做出评价，因此传统的变异算子通过无方向性地随机改变基因位，以求得更好的解;但该方法在大规模的解空间中搜索能力较弱，对总体改进较小且效率低。而本文模型中的基因位具有紧急度和延误时间的属性，可根据单个基因位的延误时间进行定向的优化，使之向延误时间减小的方向快速改进。基于此，本文提出基于紧急度的任务再分配策略（TRUD），对延误安置点重新安排配送车辆或顺序，减少延误时间，并对无延误的车辆进行运输距离上的优化;同时，以TRUD作为遗传算法的变异算子，来提高局部搜索能力。

局部搜索算子TRUD主要算法步骤如下：

1）随机选择一个回路，找到其中被延误时间最长的安置点。

2）在其他回路中寻找被延误的安置点，若存在，跳转到第3）步，否则跳转到第4）步。

3）将两个安置点交由对方的车辆负责配送，若无改进，进入第4）步。

4）将延误的安置点交由车队中运输时间最短的车辆进行配送（满足容量限制的条件下）。首先将其放在队列末尾，计算适应度函数，若无改进，前移一位，直至取得更优解或移动到首位停止。检查染色体中各基因位（即各安置点）的紧急度，若同一个回路内存在紧急度高的点位于紧急度低的点后面，调换其位置。若换位后总延误时间下降，则继续向前进行换位，直到无改进为止。紧急度值越小表示越紧急，图1中2号安置点紧急度高于1号安置点，应对其进行换位。

5）随机选择一个回路检测其延误情况，若有延误则跳转到第6）步，否则跳转到第7）步。

6）检查位于当前延误点之前一个安置点的紧急度，若较当前延误点紧急，则无需调整;相反，若比延误点小则二者换位。若换位后总延误时间和总运输时间均更优，则继续向前换位，直至无改进为止。

7）随机选择本回路内两个安置点进行换位操作，若有改进则保留，若无改进则结束本次变异。

2.4 初始化种群

在解决基本的VRP时，初始种群一般采用随机产生所有个体，该方法存在初始种群优秀个体数量少、整体适应度低、算法搜索时间长、收敛速度慢等问题。针对上述情况，本文在初始化种群阶段综合使用三种算法：随机生成、按紧急度排序和最近邻域（Nearest Neighborhood）优化。

1）随机产生一个安置点序列，将其按顺序逐个安排给第一辆车，同时计算其需求量累加之和，一旦达到一辆车的车辆容量限制即停止加入，保留这辆车最大能承载的需求点集合，则该车配送方案生成。将剩余未安排的安置点继续按顺序安排到下一辆车，直至所有安置点均安排完毕。

2）使用最近鄰域算法和紧急度排序法各生成5～10个较优解，替换掉种群中适应度最差的几个个体。

2.5 选择

使用轮盘赌算法选择优秀的个体和基因，其基本思想是个体被选中的概率与其适应度函数值成正比，而非机械地按照适应度大小来选择。这种做法可保持种群的基因多样性，避免早熟。设群体大小为n， 个体i的适应度为Fi， 则个体i被选中遗传到下一代群体的概率为：

Pi=Fi / ∑ n i=1 Fi

（8）

在迭代过程中采用精英策略，本代最好的个体直接复制到下一代种群中，保证优秀基因的延续。

2.6 交叉算子

交叉操作是将两条染色体选取一点，对换选定区域，以达到产生基因型不同的新个体的效果。本文采用的交叉方法是交换父代双方的部分序列顺序信息。

交叉算子具体算法步骤如下：

图2所示两个染色体P1和P2，每个染色体含有3辆车产生的3个子集回路。

1）在两个染色体中各随机选择一个子集，得到集合a和b。

2）若 | a∩b | ≥2，转步骤3），否则返回步骤1）。

3）以子集a={4， 5， 6， 10}和子集b={8， 6， 4， 9}为例，a∩b={4， 6}。检查两个集合中元素4、6的先后顺序是否一致，一致则转到步骤1），否则转到步骤4）。

4）分别将两个集合中元素4、6的顺序按对方的元素顺序进行调换，交叉后所得个体如图3所示，可以看出子代染色体C1、C2具有融合后的父代遗传信息。

算法步骤在哪里，不可能是图2吧？

3 实验仿真及分析

3.1 算例描述与实验设置

实验数据集包括1个仿真算例和16个来自VRP标准数据集的算例，其中仿真算例根据M地区地理条件模拟产生。

实验中提到的总运输时间指车队所有车辆各自运输时间的数值之和，总延误时间同理。

本文中所有算法均采用Java语言实现，实验环境为主频3.4GHz的Intel Core i5-7500 CPU，内存8GB的硬件平台，种群规模200，适应度参数α=0.75，交叉概率08，局部搜索概率01，设置最大迭代次数为600，每个算例均进行30次独立的计算取平均值。

3.2 结果分析

1）M地区救灾路径规划仿真实验结果分析。

M地区地理条件易发生泥石流灾害，现模拟M地区发生特大泥石流，在当地设置19个灾民安置点，救灾部门派出3辆容量为100的救灾车装载物资运往灾区，车速设置为30km/h。安置点位置和紧急度已知，见表2。

表2列出了每个安置点的编号、坐标（X、Y为安置点横纵坐标，单位为km）、物资需求量（Q）、紧急度（URG）和使用四种算法各自求得的延误时间（单位为min）。

其中：序号为0的点是出发点物资仓库;对于提前到达或准时到达的安置点，其延误时间均记为0;

URG的数值模拟灾民的不同需求，设置在180～600min区间。

表3中对比了四种算法的物资配送延误时间。

对比算法包括：

先来先服务（First Come First Served， FCFS）算法，表示按照安置点报告的顺序进行配送;

按紧急度排序（Sort by URGency， URGS）算法，对救灾车辆分配到的任务严格按照各安置点的紧急度进行配送，而且不考虑距离的远近;

TRUD-GA为本文算法，对延误时间和总运输时间加权求解;

GA为TRUD-GA去除改进初始解和变异算子后的算法，用以验证本文加入算子TRUD的有效性。

其中：FCFS表示按照安置点报告的顺序进行配送;URGS表示对救灾车辆分配到的任务严格按照各安置点的紧急度进行配送，而且不考虑距离的远近;TRUD-GA为本文算法，对延误时间和总运输时间加权求解;GA为TRUD-GA去除改进初始解和变异算子后的算法，用以验证本文加入算子TRUD的有效性。

以先来先服务（First Come First Served， FCFS）、按紧急度排序（Sorting algorithm based on URGency， URGS）、GA 、TRUD-GA（GA with TRUD）

为列名的四列数据分别表示该算法求得的每一个安置点的延误时间。对于提前到达或准时到达的安置点，其延误时间均记为0。序号为0的点是出发点物资仓库。X、Y单位为km，URG、FCFS、URGS、GA、TRUD-GA单位为min。

从表2和表3可以看出：在四种算法中，FCFS算法延误时间中位数接近2h，最长延误时间甚至达到2.5h以上，延误点数也多达7个;而URGS算法虽然总延误时间和延误点数比FCFS算法有所减少，但总体效果依然不理想，尤其是最长延误时间仍接近2h;GA有1个安置点延误，延误时间为8.6min;而算法TRUD-GA则做到了没有任何延误。由此可见TRUD-GA在总延误时间、最长延误时间上均优于FCFS、URGS和GA。

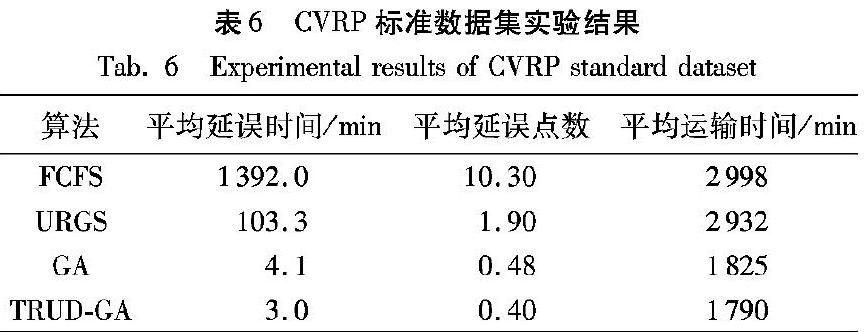
2）CVRP标准数据集实验结果分析及TRUD算子局部搜索性能验证。

实验数据来自VRP国际标准数据集，可从网站http：//neo.lcc.uma.es/vrp/vrp-instances/下载。数据集包含不同需求点数量、需求点位置、车辆数量和容量的多个算例。由于标准算例中无截止时间参数，因此本实验使用随机函数给每个需求点设置了物资配送的截止时间。设定车辆行驶速度为60km/h，并求出救灾车辆到达每个安置点的时间，统计总延误时间和总行驶时间。表4列出了相关算例的具体参数，其中：n表示安置点数量，m表示车辆数，c表示车辆容量。

为了验证算法的魯棒性，每个算例进行2次不同截止时间参数设置，共16组仿真实验，同一算例因紧急度设置不同而分别编号，例如A-n32-k5-u1与A-n32-k5-u2，结果如表5所示。URG的数值在90～840min随机生成。实验对比了FCFS、URGS、GA和本文算法TRUD-GA，对每种算法记录以下三个指标：TPT表示车队总的运输时间，DEL表示车队总延误时间，单位均为min;NUM表示配送延误的安置点数量。这三个指标的数值均越小越好。

由表5可知，在大多数算例中，TRUD-GA与其他对比算法相比延误时间最小，虽然在一些算例中延误时间比URGS算法略有增加，但总运输时间与URGS算法相比则大量减少。如算例A-n61-k9-u1，URGS算法总运输时间为3034min，延误时间为0，而TRUD-GA总运输时间为1996min，延误时间为1.8min，仅增加了1.8min延误，而总时间降低了34.2%。

由表6可知，与FCFS算法相比，TRUD-GA的平均延误时间降低了99.7%，平均延误点数降低了96.1%，平均运输时间降低了40.2%;

与URGS算法相比，TRUD-GA的平均延误时间降低了97.1%，平均延误点数降低了78.9%，平均运输时间降低了38.9%;

与GA相比，TRUD-GA的平均延误时间降低了25.0%，平均延误点数降低了16.7%，而平均运输时间降低了1.9%。

表6还统计了各算法的延误时间标准差，TRUD-GA为1.35，小于FCFS、URGS和GA，可见其求解性能稳定，对不同算例求解时鲁棒性优于对比算法。

由表2、3、5、6中TRUD-GA与GA的实验结果对比可知，本文提出的局部搜索算子TRUD对实验结果起到了比较明显的改进作用。

为了进一步直观地验证TRUD算子的局部搜索性能，对TRUD-GA与无TRUD算子的遗传算法GA的迭代过程进行比较，它们在算例A-n39-k6、A-n45-k6、A-n69-k9、 A-n80-k10上的运行结果如图4。由于适应度函数是极小化的，所以适应度函数值越小越好。从图4中可以看出，在600代迭代过程中，TRUD-GA一直保持着持续收敛的趋势，且不同规模的4个算例中取得的最优解均好于GA。由此可见TRUD算子具有优秀的局部搜索性能和全局收敛能力，同时也表现出了良好的鲁棒性。

3.3 决策偏好参数分析

适应度函数中的决策偏好参数α决定了算法优化的方向：取值趋向0时偏好于总运输时间最小化，也即总距离最小化;取值趋向1时偏好总延误时间最小化。紧急度和系数α都是算法优化时的重要参数，紧急度是算法使用者无法控制的，而α可由使用者调节，在不增加延误时间的前提下降低总运输距离和时间。为验证参数α的应用效果，现对所有算例进行不同α取值的对比实验。每组实验运行30次取平均值，结果如表7所示。

可以看出，随着α取值的增大，总延误时间逐渐减小，延误点数逐渐减少，总运输时间逐渐增加。对于大多数算例，例如A-n45-k6，在α=0.75时平均延误时间为1.2min，因为上述结果是运行30次的平均值，此时已经能以较大概率取得最优解;而在α=0.99时，其延误时间为0，但总运输时间却比α=0.75时有一定程度的增加，因此验证了参数α取0.75的合理性。而对于个别特殊的算例，其安置点间距很大，难以在规定截止时间内配送，α=0.75时物资配送仍有较为明显的延误情况发生，例如算例A-n80-k10，此时设置α=099可减少平均延误时间12.4min，延误安置点数量减少平均1.1个，说明了决策偏好参数α对优化方向起到的作用。

通过以上对比实验可以得出结论：使用TRUD-GA求解考虑紧急度的应急救灾车辆路径问题，灾区安置点的物资配送总延误时间、延误安置点数量、车辆总运输时间相比其他算法均有明显下降，求解过程说明TRUD-GA具有良好的收敛性以及寻优能力。通过对决策偏好参数α的不同设置分析，说明了TRUD-GA具有良好的适用性。

4 结语

本文依据救灾工作的现实要求——最小化救灾车辆延误时间和最小化总运输时间的两个目标，设计了基于紧急度的混合遗传算法，提出了基于紧急度的任务再分配算子TRUD，对应急物资调度路线进行有针对性的优化。对实验结果的分析表明，TRUD算子有着良好的局部搜索能力，以TRUD为局部搜索算子的混合遗传算法TRUD-GA可以显著降低物资配送延误时间和总体运输时间。本文模型中的路径状态为完全畅通，而在灾情突发的情况下会存在路径拥堵，因此如何在灾区路况不同的情况下设计动态的救灾物资调度策略还需进一步的研究。

参考文献

[1] LI Q， TU W， ZHUO L. Reliable rescue routing optimization for urban emergency logistics under travel time uncertainty [J]. International Journal of Geo-Information， 2018， 77（7）： 1-21.

[2]  徐浩，李佳川，韩传峰.震后运速受限条件下的多目标定位：路径问题研究[J].管理工程学报，2017，31（4）：147-155. （XU H， LI J C， HAN C F. Multi-target localization under the condition of limited speed after earthquake： research on path problem[J].Journal of Industrial Engineering/Engineering Management，2017，31（4）：147-155.）

[3] 張国富，王永奇，苏兆品，等.应急救援物资多目标分配与调度问题建模与求解[J].控制与决策，2017，32（1）：86-92. （ZHANG G F， WANG Y Q， SU Z P， et al. Modeling and solving multi-objective allocations-cheduling problem for emergency relief materials[J]. Control and Decision， 2017， 32（1）： 86-92.）

[4] SHAHPARVARI S， ABBASI B， CHHETRI P， et al. Vehicle routing and scheduling for bushfire emergency evacuation [C]// Proceedings of the 2015 IEEE International Conference on Industrial Engineering and Engineering Management. Piscataway， NJ： IEEE， 2015： 696-700.

[5] HE Y， WEN J， HUANG M. Study on emergency relief VRP based on clustering and PSO [C]// Proceedings of the 11th International Conference on Computational Intelligence and Security. Washington， DC： IEEE Computer Society， 2015： 43-47.

[6]  石建力，张锦.需求点随机的分批配送VRP模型与算法研究[J].控制与决策，2017，32（2）：213-222. （SHI J L，ZHANG J.Model and algorithm for split delivery vehicle routing problem with stochastic customers[J].Control and Decision，2017，32（2）：213-222.）

[7] ZHAO J， GUO Y， DUAN X. Dynamic path planning of emergency vehicles based on travel time prediction [J]. International Journal of Communications， Network and System Sciences， 2018， 11（2）： Article ID： 9184891.

[8] LIU J， XIE K. Emergency materials transportation model in disasters based on dynamic programming and ant colony optimization [J]. Kybernetes， 2017， 46（4）： 656-671.

[9] QIN J， YE Y， CHENG B， et al. The emergency vehicle routing problem with uncertain demand under sustainability environments [J]. Sustainability， 2017， 9（3）： 1-24.

[10] ZHENG Y， LING H. Emergency transportation planning in disaster relief supply chain management： a cooperative fuzzy optimization approach [J]. Soft Computing， 2013， 17（7）： 1301-1314.

[11]   易云飞，蔡永乐，董文永，等.求解带用户满意度的多目标实时车辆路径问题的改进伊藤算法[J].电子学报，2015，43（10）：2053-2061. （YI Y F， CAI Y L， DONG W Y， et al. Improved ITO algorithm for multiobjective real-time vehicle routing problem with customers satisfaction [J].Acta Electronica Sinica，2015，43（10）：2053-2061.）

[12] 任錫德，朱建明，王晶，等.考虑均衡性的不确定时间车辆调度问题研究[J].运筹与管理，2013，22（2）：86-91. （REN X D， ZHU J M， WANG J， et al. Research on load-balancing vehicle routing problem with uncertain travel time [J]. Operations Research and Management Science， 2013， 22（02）： 86-91.）

[13]  文仁强，钟少波，袁宏永，等.应急资源多目标优化调度模型与多蚁群优化算法研究[J].计算机研究与发展，2013，50（7）：1464-1472. （WEN R Q， ZHONG S B， YUAN H Y， et al. Emergency resource multi-objective optimization scheduling model and multic-olony ant optimization algorithm for emergency resources [J].Journal of Computer Research and Development，2013，50（7）：1464-1472.）

[14] 徐志宇，张杰，彭嘉臻，等.应急物流的分批配送模型及亚启发式算法求解[J].系统仿真学报，2012，24（12）：2500-2505， 2510. （XU Z Y， ZHANG J， PENG J Z， et al. Split delivery model and metaheuristic approach for emergency logistics [J]. Journal of System Simulation， 2012， 24（12）： 2500-2505， 2510.）

[15] 朱建明，黄钧，刘德刚，等.突发事件应急医疗物资调度的随机算法[J].运筹与管理，2010，19（1）：9-14. （ZHU J M， HUANG J， LIU D G， et al. Randomized algorithm for vehicle routing model for medical supplies in large-scale emergencies [J]. Operations Research and Management Science， 2010， 19（1）： 9-14.）