基于多尺度双线性卷积神经网络的多角度下车型精细识别

刘虎 周野 袁家斌

摘 要：针对多角度下车辆出现一定的尺度变化和形变导致很难被准确识别的问题，提出基于多尺度双线性卷积神经网络（MS-B-CNN）的车型精细识别模型。首先，对双线性卷积神经网络（B-CNN）算法进行改进，提出MS-B-CNN算法对不同卷积层的特征进行了多尺度融合，以提高特征表达能力;此外，还采用基于中心损失函数与Softmax损失函数联合学习的策略，在Softmax损失函数基础上分别对训练集每个类别在特征空间维护一个类中心，在训练过程中新增加样本时，网络会约束样本的分类中心距离，以提高多角度情况下的车型识别的能力。实验结果显示，该车型识别模型在CompCars数据集上的正确率达到了93.63%，验证了模型在多角度情况下的准确性和鲁棒性。

关键词：车型精细识别;卷积神经网络;双线性卷积神经网络;中心损失;多尺度

中图分类号： TP391.4

文献标志码：A

Fine-grained vehicle recognition under multiple angles based on multi-scale bilinear convolutional neural network

LIU Hu， ZHOU Ye*， YUAN Jiabin

College of Computer Science and Technology， Nanjing University of Aeronautics and Astronautics， Nanjing Jiangsu 210000， China

Abstract： In view of the problem that it is difficult to accurately recognize the type of vehicle due to scale change and deformation under multiple angles， a fine-grained vehicle recognition model based on Multi-Scale Bilinear Convolutional Neural Network （MS-B-CNN） was proposed. Firstly， B-CNN was improved and then MS-B-CNN was proposed to realize the multi-scale fusion of the features of different convolutional layers to improve feature expression ability. In addition， a joint learning strategy was adopted based on center loss and Softmax loss. On the basis of Softmax loss， a category center was maintained for each category of the training set in the feature space. When new samples were added in the training process， the classification center distances of samples were constrained to improve the ability of vehicle recognition in multi-angle situations. Experimental results show that the proposed vehicle recognition model achieved 93.63% accuracy on CompCars dataset， verifying the accuracy and robustness of the model under multiple angles.

Key words： fine-grained vehicle recognition; Convolutional Neural Network （CNN）; Bilinear Convolutional Neural Network （B-CNN）; center loss; multi-scale

0 引言

車型精细识别是智能交通系统的核心技术。所谓的车辆精细型号识别指的是对车辆的品牌、型号、年代的识别。通过现有技术自动识别出车辆精细型号，可以显著提高交通执法的效率。在与车辆相关的犯罪案件中，公安部门往往需要借助受害者对车辆特征的描述，从海量的交通图像数据库中检索可疑车辆。不同于传统的车牌识别，对车辆进行精细识别得到汽车制造商和具体型号信息，有利于对车辆进行在线或离线检索和识别。此外，通过将识别得到的信息与车管所车辆的注册信息进行对比，可以快速锁定假牌、套牌车，极大地提高相关案件的处理效率。在交通监控中，与车辆型号相关的车辆流量统计在智能交通系统中发挥了更重要的作用：估计监控点之间的行程时间并在高峰时段提供详细的交通状况可以很好地缓解交通拥堵。此外，车辆精细型号识别在智慧停车、智能车险、高速公路智能收费等领域有着重要应用。总之，随着监控摄像机的普及，车型精细识别具有重大的实用价值和经济价值[1]。

车型精细识别属于细粒度图像分类的一种。细粒度图像分类是目前人工智能领域的热门研究课题，涉及计算机视觉、模式识别、图像处理、概率论与数理统计等多个学科， 引起了国内外学者的广泛关注。Xiao等[2]提出了两级注意力（Two level attention）算法，该方法不需要人工标注框等人工标注信息。Liu和他的研究团队[3]提出了全连接层（Fully Convolutional Network，FCN）注意力模型，该模型是一种基于强化学习网络模型，可以自适应地选择多个任务驱动的注意力区域。Simon等[4]提出了星座算法（Constellations），该算法对卷积神经网络生成特征图（Feature map）进行了分析，选取响应值高的区域作为关键点，并基于关键点来提取局部区域信息。Lin等[5]提出了双线性卷积神经网络（Bilinear CNN，B-CNN），该方法通过两个子网络相互协作共同完成区域检测与特征提取的任务。不同于上述方法，B-CNN是一种端到端的模型，它将区域检测与特征提取任务相结合，达到了相互促进的目的。

目前，研究者针对车型精细识别问题提出了许多解决方法。Sullivan等[6]通过建立一个三维模型去模拟车辆的姿态，利用三维模型信息得到车辆的姿态位置，并将其投影到二维平面，进而提取二维平面的特征去实现车辆的匹配识别。而Li等[7]对Sullivan的工作进行了改进，在拟合出了车辆的三维模型后，直接将车辆的3D信息用于分类。基于三维信息的车型识别可以在一定程度上降低多视角给识别带来的影响，但该方法需要为每一种车型建立三维模型，随着车型数量的增加，特征提取、图像表示和模型匹配等环节将变得更加复杂，带来巨大的计算开销。随着对车辆间细节识别需求的逐步增加，如何准确描述车辆的细节、如何区分不同车辆之间的细微差别是当前车辆识别的研究热点和问题[8]。Fang 等[9]提出了一个由粗到精的卷积神经网络模型，并根据卷积神经网络最后一个卷积层的特征图自动定位局部区域并提取局部特征，将局部特征与车辆整体特征进行融合，并训练支持向量机（Support Vector Machine，SVM）分类器。但是，上述方法都是针对限定角度下的车型精细识别。

为了解决多角度下车型精细识别问题，从建立提取能力强的网络模型和使用基于中心损失的度量学习方法两方面着手：首先对B-CNN算法进行了改进，提出了多尺度双线性卷积神经网络（Multi Scale B-CNN，MS-B-CNN），它对不同卷积层的特征进行了多尺度融合，能提高特征表达能力;然后引入中心损失，对车辆图像在特征空间内加以约束，有效地引导网络学习使得类内距离较小、类间距离较大的特征。

1 相关知识

1.1 B-CNN

B-CNN的算法流程如图1所示。

B-CNN模型由一个四元组组成：M=（fA， fB，p，c），其中fA和fB为基于卷积神经网络A和B的特征提取函数，p是一个池化函数，c是分类函数。特征提取函数可以看成一个函数映射，将输入图像I与位置区域L映射为一个c×D维的特征。输入图像在某一位置l处的双线性特征可通过如下公式表示：

bilinear（l，I， fA， fB）=fA（l，I）TfB（l，I）

（1）

之后利用池化函数p将所有位置的双线性特征进行累加汇聚为一个双线性特征，并用这个特征来描述输入图像的特征：

Φ（Ι）=∑ l∈L bilinear（l，I， fA， fB）

（2）

最后，分类函数c对提取到的特征进行分类，可以采用SVM分类器或者逻辑回归。

将B-CNN应用于实际场景中是一个端到端的训练过程。模型的前半部分是基本卷积神经网络模型，因此只要求得后半部分的梯度值，即可完成对整个模型的训练[10]。对于每个位置l，特征提取函数fA和fB的输出分别为 f 1与 f 2，那么在l处的双线性特征是x= f T1 f 2。用dl/dx表示损失函数在x处的梯度值，通过链式法则可得损失函数对A和B网络输出的梯度值：

dl dA =B  dl dx  T

（3）

dl dB =A  dl dx  T

（4）

关于B-CNN的直观解释是，网络A的作用是对物体进行定位，網络B用于提取网络A检测到的对象的特征。两个网络相互协调作用，完成细粒度图像分类过程中两个最重要的任务：区域检测和特征提取[10]。

1.2 度量学习

度量学习又叫距离度量学习，通过从给定的训练样本集学习，获得可以有效反映数据样本之间距离的度量矩阵。基于度量矩阵的新特征空间中，相同类别样本的分布更紧密，而不同类别样本的分布更松散。度量学习就是学习一个映射空间（Embedding Space），使具有相同标签的样本在映射空间内尽量靠近，具有不同标签的样本在嵌入空间中尽量远离。

随着深度学习的发展，度量学习也可以利用深度网络对特征抽取的能力。针对某个二元组、三元组中不同的样本，其对应的深度网络之间会共享参数，并在最后一层计算样本间的欧氏距离来度量特征表示的优劣。不同的损失函数能够考虑样本之间的异构性、类别之间的差异性，以及更全面地利用当前通过网络的样本。学到的特征表示可以用于图像细粒度分类、聚类，人脸识别等任务。

目前，最流行的度量学习方法是使用三元组损失（Triplet Loss）[11]和中心损失（Center Loss）[12]。

1.2.1 三元组损失

三元组损失最早被用在人脸识别任务中，每次在训练集中取出三个样本组成三元组（ x ai， x pi， x ni），第一个样本 x ai被称为Anchor，第二个样本 x pi与 x ai是同类被称为Positive，第三个样本 x ni与 x ai是异类被称为Negative。在这样的三元组中，距离‖f（ x ai）-f（ x pi）‖2应该较小，‖f（ x ai）-f（ x ni）‖2应该较大。三元组损失希望如下式子成立：

‖f（ x ai）-f（ x pi）‖22+α<‖f（ x ai）-f（ x ni）‖22

（5）

即同类别样本间的距离平方至少要比不同样本间的距离平方小α。因此三元组的损失函数为：

Li=[‖f（ x ai）-f（ x pi）‖22+α-‖f（ x ai）-f（ x ni）‖22]+

（6）

其中，距离取平方是为了后续求导方便。

三元组损失直接对样本特征向量间的欧氏距离进行优化，但是在训练的过程中，三元组的选择是很有挑战性的。如果每次都随机选择三元组，尽管模型可以正确地收敛，但是达不到最佳性能。如果加入“难例挖掘”，也就是说，每次选择最难以区分的三元组进行训练，模型又往往不能正确地收敛。对此，建议选取那些“半难”（Semi-hard）的数据进行训练，这样让模型在可以收敛的同时，又可以保持良好的性能。 此外，使用三元组损失训练模型通常还需要非常大的数据集，才能取得较好的效果。

1.2.2 中心损失

与三元组损失不同，中心损失没有直接对距离进行优化，它保留了原有的分类模型，但又为每个类（在车型精细识别模型中，一个类就对应一个车型）指定了一个类别中心。同一类别的图像的特征向量都尽量靠近自己的类别中心，尽量远离不同类的类别中心。令输入样本为 x i，该样本对应的类别为yi，类别yi的类别中心为 c yi。那么中心损失函数的定义为：

Lcenter_loss= 1 2 ∑ N i=1 ‖ x i- c yi‖22

（7）

中心损失函数一个很重要问题就是类别中心 c yi的选择。理论上来说，类别yi所有样本特征向量的平均值是其最佳中心。可是这种方式并不切实际，如果使用这种方式，那么在每次迭代时，都要对所有样本计算一次 c yi，这会带来极大的运算成本。因此，正确的做法是，在初始阶段，先随机确定每个类的类别中心，然会针对每个batch进行更新。此外，还需要设置类别中心学习率α来控制免错分类样本对类别中心的计算带来的干扰。式（8）与式（9）分别为Lcenter_loss关于 x i的梯度表达式和类别中心 c yi的更新公式：

Lcenter_lossx i = x i- c yi

（8）

Δ c j= ∑ m i=1 δ（yi=j）·（ c j- x i） 1+∑ m i=1 δ（yi=j）

（9）

其中：δ（yi=j）是一个指示性函数，yi等于j时，其值为1，反之为0;α为区间[0，1]内的一个值。

2 本文方案构造

本文对B-CNN进行了研究，提出了多尺度B-CNN算法MS-B-CNN。MS-B-CNN对不同卷积层的特征进行了多尺度融合，以提高特征表达能力。此外，本章采用了基于中心损失与Softmax联合学习的策略，在 Softmax基础上分别对训练集每个类别在特征空间维护一个类中心，训练过程新增加样本时，网络会约束样本的分类中心距离，提高多角度情况下的车型识别的能力。图2为MS-B-CNN结构。

2.1 中心损失函数的引入

在多角度车型识别问题中，同一类型的车的图片由于拍摄角度不同，映射到特征空间表示也不同，那么它们之间的距离也不尽相同，这可能会导致同一类别的车的图像在特征空间内形成了具有相对较大的类内差异的簇。受到人脸识别的启发，本章将结合度量学习，对车辆图像在特征空间内加以约束，有效地引导网络学习使得类内距离较小、类间距离较大的特征。

2.1.1 两种损失函数的比较

三元组损失侧重于增大类间距，中心损失注重减小类间距离。在车辆多角度识别中，类内距离可能会大于类间距离，因此，减小车型的类内差异显得尤为重要。此外，在三元组损失中，三元组的构造比较复杂，且依赖于难例样本（Hard Sample），比较难收敛。而中心损失函数没有复杂的构造过程，计算简单，易于收敛，因此本文将使用基于中心损失的度量学习。

然而，中心损失没有对类间距进行处理，因而可能导致不同类在映射空间出现重叠的情况。中心损失函数训练出的模型虽然有較好的可分性但是区分能力较差，在多角度车型精细识别问题中，同一类别的车在不同角度下可能出现类内差距大于类间差距的问题，就必须要求多角度车型识别模型提取到的特征不仅要有可分性，还要有判别性。通过训练和学习，可以减少或限制相似样本之间的距离，并增加不同类别样本之间的距离。

本文采用中心损失与Softmax损失联合学习的方式。这样，模型在中心损失函数和Softmax损失函数的联合监督下训练，通过Softmax损失使得不同类别的特征向量具有判别性，而中心损失又使同一类别下的特征向量具有内聚性，不仅增强了特征向量类间的判别性，还增强了特征向量类内的紧凑性。

2.1.2 Softmax损失与中心损失的联合学习策略

经典B-CNN中用的损失函数正是Softmax损失，Softmax层的输出是一个向量，表示输入图像属于每一类的概率。在车型识别问题中，假设有 k 个车型，那么Softmax的输出是一个K维向量。对于 m 个样本，为训练集及其所对应的标签为： {（ x （1），y（1）），（ x （2），y（2）），…，（ x （m），y（m））}。当输入样本为 x （i）时，其 k 个估计概率用如下公式表示：

其中， W 1， W 2，…， W k为网络模型的参数。 1 ∑ k j=1 e W Tj x （i） 对输出向量进行了归一化。在模型训练时，采用梯度下降法对Softmax损失函数进行优化，其损失函数如下公式所示：

前文说到，本文采用中心损失与Softmax 损失联合学习的方式，在增大类间距离的同时减小类内距离，使其获得的特征具有更强的识别能力，那么网络的最终目标函数形式可以表示为：

Lfinal= Lsoftmax_loss+λLcenter_loss=- 1 m  ∑ m i=1 ln e W Tl x （i） ∑ k l=1 e W Tl x （i）  + λ 2 ∑ m i=1 ‖ x i- c yi‖22

（13）

其中，λ是一个超参数，为两个损失函数间的调节系数。λ越小，类内差异占整个目标函数的比重就越小;λ越大，类内差异占整个目标函数的比重就越大，生成的特征就会具有明显的内聚性。

Softmax损失函数与中心损失函数联合学习的算法流程如下：在训练时，首先初始化网络层中的参数θc、 W 以及{ c j | j=1，2，…，n}。同时还需要设置的参数有λ、α、总迭代次数T、当前迭代次数t（初始化为0）以及学习率μ′。

那么，Softmax损失函数与中心损失函数联合学习的具体步骤如下：

1）判断网络是否收敛，不收敛则执行步骤2）;

2）迭代次数t自加1，即t←t+1;

3）计算联合损失Ltfinal=Ltcenter_loss+Ltsoftmax_loss;

4）通过式（14）对每一张图片计算反向传播误差 Ltfinalx ti ;

5）通过式（15）更新参数 W ;

6）通过公式 c t+1j= c tj-α·Δ c tj更新参数 c j;

7）通过式（16）更新参数θc;

8）网络收敛或达到最大迭代次数，则结束循环，否则从步骤1）开始重复执行。

2.2 多尺度特征融合

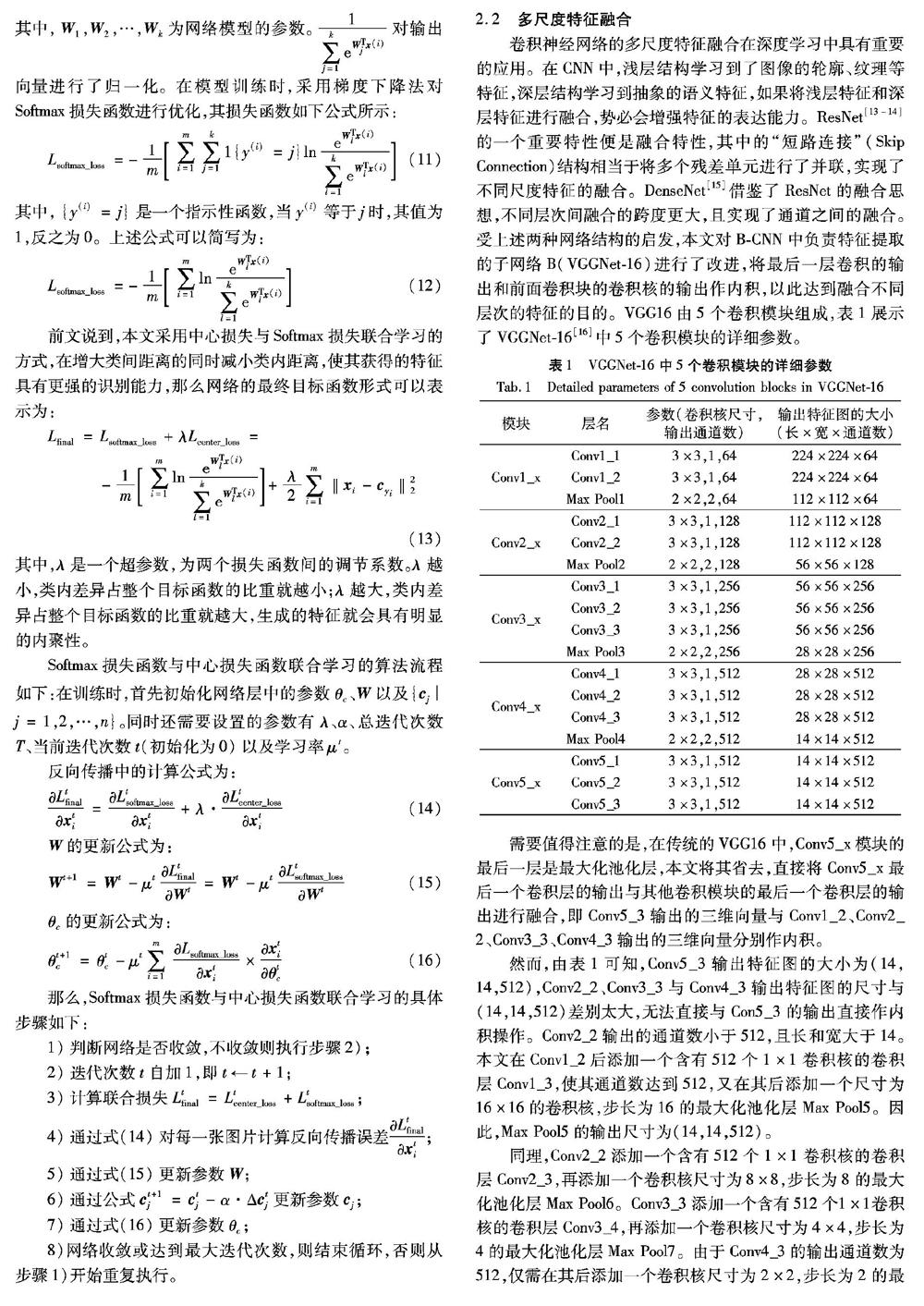
卷积神经网络的多尺度特征融合在深度学习中具有重要的应用。在CNN中，浅层结构学习到了图像的轮廓、纹理等特征，深层结构学习到抽象的语义特征，如果将浅层特征和深层特征进行融合，势必会增强特征的表达能力。ResNet[13-14]的一个重要特性便是融合特性，其中的“短路连接”（Skip Connection）结构相当于将多个残差单元进行了并联，实现了不同尺度特征的融合。DenseNet[15]借鉴了ResNet的融合思想，不同层次间融合的跨度更大，且实现了通道之间的融合。受上述两种网络结构的启发，本文对B-CNN中负责特征提取的子网络B（VGGNet-16）进行了改进，将最后一层卷积的输出和前面卷积块的卷积核的输出作内积，以此达到融合不同层次的特征的目的。VGG16由5个卷积模块组成，表1展示了VGGNet-16[16]中5个卷积模块的详细参数。

需要值得注意的是，在传统的VGG16中，Conv5_x模块的最后一层是最大化池化层，本文将其省去，直接将Conv5_x最后一个卷积层的输出与其他卷积模块的最后一个卷积层的输出进行融合，即Conv5_3输出的三维向量与Conv1_2、Conv2_2、Conv3_3、Conv4_3输出的三维向量分别作内积。

然而，由表1可知，Conv5_3输出特征图的大小为（14，14，512），Conv2_2、Conv3_3与Conv4_3输出特征图的尺寸与（14，14，512）差别太大，无法直接与Con5_3的输出直接作内积操作。Conv2_2输出的通道数小于512，且长和宽大于14。本文在Conv1_2后添加一个含有512个1×1卷积核的卷积层Conv1_3，使其通道数达到512，又在其后添加一个尺寸为16×16的卷积核，步长为16的最大化池化层Max Pool5。因此，Max Pool5的输出尺寸为（14，14，512）。

同理，Conv2_2添加一个含有512个1×1卷积核的卷积层Conv2_3，再添加一个卷积核尺寸为8×8，步长为8的最大化池化层Max Pool6。Conv3_3添加一个含有512个1×1卷积核的卷积层Conv3_4，再添加一个卷积核尺寸为4×4，步长为4的最大化池化层Max Pool7。由于Conv4_3的输出通道数为512，仅需在其后添加一个卷积核尺寸为2×2，步长为2的最大化池化层Max Pool8即可。

令Conv5_3、Max Pool5、Max Pool6、Max Pool7与Max Pool8的输出特征图分别为 Fm 1、 Fm 2、 Fm 3、 Fm 4与  Fm 5，大小均為（14，14，512）。然后，通过通道位置变换（Transpose）和重新调整大小（Reshape）后，如图3所示， Fm 1的尺寸为（512，196）， Fm 2、 Fm 3、 Fm 4、 Fm 5的尺寸为（196，512），经过内积操作后得到特征  bf 1、 bf 2、 bf 3和 bf 4。此外，子网络A与子网络B最后一层卷积层输出作内积得到特征 bf 0。 bf 0、 bf 1、 bf 2、 bf 3和 bf 4均为长度为262144（512×512）的一维向量。将这5个连接（Contact）在一起得到长度为1310720的一维向量。然后连接一个隐藏层节点数为8192的全连接层FC1，然后连接一个Dropout层，在训练时节点保留率为0.5，预测是为1。接下来是一个和前面一样的全连接层FC2，隐藏层节点数为1024。

3 实验及结果分析

本节仍使用平均准确率（Average Precision， AP）和平均召回率（Average Recall， AR）作为评价指标。联合损失函数中的超参数α默认为0.5。

3.1 数据集介绍

本文使用CompCar[17]车型数据集，该数据集由香港中文大学的多媒体实验室制作，是目前最大的汽车开源数据集。从CompCars中选取了生活常见的117种车型，包括12018张训练图片和3122张测试图片，训练集和训练集中每个车型类别包含的样本数量不一，但大致平衡。数据集中包含五个角度的车辆图像：正面、侧面、正侧面、右侧面、背面，如图4所示。

3.2 实验环境

本文实验所采用的计算机为Red Hat 4.8.3-9操作系统，64GB内存，处理器为Intel Xeon CPU E5-2609 v2 2.5GHz 且配置了NVIDIA Tesla K40m的图形处理单元， Tesla K40m是基于Fermi CUDA（Compute Unified Device Architecture）架构的GPU，12GB显存，含有2880个CUDA 核心，双精度浮点性能1.43Tflops，单精度浮点性能：4.29Tflops。

3.3 超参数λ的选取

λ在[0，1]区间内变化，学习到了不同的模型。图5为不同λ值下的车型识别平均正确率。λ=0和λ=1时结果相对最差：当λ=0时，车型识别的平均准确率为85.52%，说明仅使用Softmax损失函数是不可取的;当λ=1时，车型识别平均准确率为81.37%，说明此时模型过分侧重于减少类内差距，即侧重于学习特征的“内聚性”，而忽略了增大类间距，从而导致模型分类效果较差。当λ取0.001时，模型的分类正确率最高，达到了93.63%，此时模型在增大类间距和减小类内距之间取得了很好的平衡。

3.4 多尺度融合对实验结果的影响

本实验将MS-B-CNN的分类结果和基于本框架但没有多尺度特征融合的B-CNN的分类结果进行了对比，结果如表2。由表2可以看出，使用经典B-CNN算法的平均正确率为92.56%，平均召回率为89.70%;采用多尺度特征融合的方式后的平均正确率为93.63%，平均召回率为92.65%，两个指标均有所提升，从而验证了本文采用的多尺度融合方法的有效性。

3.5 中心损失对实验结果的影响

本节还对不同角度下的车型识别情况进行了分析。由表3可看出，基于本文框架，车辆正面和背面图像的识别准确率为95.73%和95.26%，平均召回率为93.55%和94.04%，结果明显好于其他三个角度，这说明车辆的正面和侧面角度的图像区分度较大，而前侧面、后侧面、侧面角度图像的区分度较小。角度复杂也是车辆识别算法进行跨场景迁移和实际应用的难题，因此本文结合基于中心损失的度量学习对车辆图像在特征空间内加以约束，有效地引导网络学习使得类内距离小、类间距离大的特征，来提高模型在多角度情况下的准确性和鲁棒性。通过对比实验可以看出，每个角度下车辆的识别准确率和召回率都有了明显提升，从而证明了本文方法的有效性。

4 结语

本文从建立提取能力强的网络模型和使用基于中心损失的度量学习方法两方面对多角度下车型精细识别进行了研究，提出了MS-B-CNN，提高了特征表达能力， 并且采用Softmax损失和中心损失联合学习的方式提高了多角度情况下的车型识别的能力。最终，本文方法在CompCars数据集中选取的117种常用车型中取得了93.63%的平均正确率。本文所研究的车型精细识别均是在车辆没有被遮挡的情况，然而，在现实生活中，经常出现车辆被遮挡的情况，因此，下一步将对遮挡情况下的车型精细识别进行探究。

参考文献

[1] 许可.基于卷积神经网络的细粒度车型识别[D]. 哈尔滨：哈尔滨工程大学， 2015： 1. （XU K. Fine grained vehicle identification based on convolutional neural network [D]. Harbin： Harbin Engineering University， 2015： 1.）

[2] XIAO T， XU Y， YANG K， et al. The application of two-level attention models in deep convolutional neural network for fine-grained image classification [C]// Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway， NJ： IEEE， 2015： 842-850.

[3] LIU X， XIA T， WANG J， et al. Fully convolutional attention networks for fine-grained recognition [J]. arXiv E-print， 2017： arXiv：1603.06765.

[4] SIMON M， RODNER E. Neural activation constellations： Unsupervised part model discovery with convolutional networks [C]// Proceedings of the 2015 IEEE International Conference on Computer Vision. Piscataway， NJ： IEEE， 2015： 1143-1151.

[5] LIN T-Y， ROYCHOWDHURY A， MAJI S， et al. Bilinear CNNs for fine-grained visual recognition [J]. arXiv E-print， 2017： arXiv：1504.07889.

[6] SULLIVAN G D， BAKER K D， WORRALL A D， et al. Model-based vehicle detection and classification using orthographic approximations [J]. Image and Vision Computing， 1997， 15（8）： 649-654.

[7] LI L-J， SU H， LI F， et al. Object bank： a high-level image representation for scene classification & semantic feature sparsification [C]// Proceedings of 2010 Conference and Workshop on Neural Information Processing Systems. North Miami Beach， FL： Curran Associates Inc.， 2010： 1378-1386.

[8] 張强， 李嘉锋， 卓力. 车辆识别技术综述[J]. 北京工业大学学报， 2018，44（3）：126-136. （ZHANG Q， LI J F， ZHUO L. Review of vehicle recognition technology [J]. Journal of Beijing University of Technology， 2018， 44（3）： 126-136.）

[9] FANG J， ZHOU Y， YU Y， et al. Fine-grained vehicle model recognition using a coarse-to-fine convolutional neural network architecture [J]. IEEE Transactions on Intelligent Transportation Systems， 2017， 18（7）： 1782-1792.

[10] 羅建豪，吴建鑫.基于深度卷积特征的细粒度图像分类研究综述[J].自动化学报，2017，43（8）：1306-1308. （LUO J H， WU J X. A survey on fine-grained image categorization using deep convolutional features [J]. Acta Automatica Sinica， 2017，43（8） ：1306-1308.）

[11]  SCHROFF F， KALENICHENKO D， PHILBIN J， et al. FaceNet： A unified embedding for face recognition and clustering [C]// Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway， NJ： IEEE， 2015： 815-823.

[12] WEN Y， ZHANG K， LI Z， et al. A discriminative feature learning approach for deep face recognition [C]// Proceedings of the 2016 European Conference on Computer Vision， LNCS 9911. Berlin： Springer， 2016： 499-515.

[13] HE K， ZHANG X， REN S， et al. Deep residual learning for image recognition [C]// Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway， NJ： IEEE， 2016： 770-778.

[14] HE K， ZHANG X， REN S， et al. Identity mappings in deep residual networks [C]// Proceedings of the 2016 European Conference on Computer Vision， LNCS 9908. Berlin： Springer， 2016： 630-645.

[15] HUANG G， LIU Z， MAATEN L van der， et al. Densely connected convolutional networks [C]// Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway， NJ： IEEE， 2017： 2261-2269.

[16] SIMONYAN K， ZISSERMAN A. Very deep convolutional networks for large-scale image recognition [J]. arXiv E-print， 2015： arXiv：1409.1556. [EB/OL].[2018-11-07].https：//arxiv.org/pdf/1409.1556.pdf.

[17] YANG L， LUO P， LOY C， et al. A large-scale car dataset for fine-grained categorization and verification[C]// Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway， NJ： IEEE， 2015： 3973-3981.