短波通信中基于自适应帧长的数据速率变化改进算法
2019-10-23王也黄国策董淑福
王也 黄国策 董淑福
摘 要:为解决传统数据速率变化(DRC)传输算法中因速率震荡造成的高误码率(BER)问题,提出一种基于自适应帧长(AFL)的DRC改进传输算法。首先,在初始化阶段,根据当前信道的参数和以往经验值信息确定初始传输的帧长和传输速率,并进行数据传输。然后,当检测到传输过程中连续两个相同长度帧发送成功后,开始增加帧长;若出现重发帧连续两次重传失败的情况,则在下次传输时将帧长减半。最后,结合当前的帧长计算误帧率,若该值小于预设的阈值,则提高数据传输速率。与RapidM DRC算法相比,该算法的链路平均BER降低了个1.8百分点,链路连通率提高了11个百分点。实验结果表明,所提算法基本消除了速率震荡的现象,能够提高短波通信系统的通信能力。
关键词:短波通信;数据速率变化;自适应帧长;电离层通信
中图分类号: TN911.7
文献标志码:A
Improved data rate change algorithm based on adaptive frame length in short-wave communication
WANG Ye1*, HUANG Guoce2, DONG Shufu2
1. Graduate School, Air Force Engineering University, Xian Shaanxi 710058, China ;
2.Information and Navigation College, Air Force Engineering University, Xian Shaanxi 710077, China
Abstract: To solve the high Bit Error Rate (BER) caused by rate oscillation in traditional Data Rate Change (DRC) algorithm, an improved DRC algorithm based on Adaptive Frame Length (AFL) was proposed for short-wave communication. Firstly, in the initialization phase, the frame length and transmission rate of the initial transmission were determined by the parameters of the current channel and the information of previous empirical values, and the data transmission was started. Then, if two frames with the same length were successively sent in the transmission process, the frame length would be accordingly increased. If the retransmission failed twice in a row, the frame length would be halved in the next transmission. Finally, the frame error rate was calculated based on the current frame length. The data rate would be increased if the value was less than the preset threshold. Compared with RapidM DRC, the average link BER of the proposed algorithm was decreased by 1.8 percentage points, and the link availability was increased by 11 percentage points. Experimental results show that the proposed algorithm can eliminate the rate oscillation and improve the communication capability of the short-wave communication system.
Key words: short-wave communication; Data Rate Change (DRC); adaptive frame length; ionospheric communication
0 引言
短波通信[1]因其通信距离远、资源占用少、部署灵活度高等优点,一直作为应急通信、无盲區通信的重要手段,也是军事远距离通信的保底手段[2]。但是短波信道受天气等诸多因素影响处于不稳定的状态,为了实现可靠高效的通信,出现了自动链路质量分析(Link Quality Analysis, LQA)、自动链路建立(Automatic Link Establishment, ALE)、自动数据速率变化(Data Rate Change, DRC)等技术[3]。其中变速率通信能够选择在当前信道状态下的最高数据速率[4],实现可靠高效的通信。
变速率短波通信技术的发展和应用要晚一些, 1999年,在短波数据通信标准STANAG 5066中首次提出了DRC思想,为短波通信在变速率技术发展开辟了空间。同年,又提出了基于STANAG 5066标准[5]的DRC算法[6],能够根据误帧率(Frame Error Rate, FER)逐级调整数据速率。随后文献[7]中提出了基于STANAG 4369标准的Trinder DRC算法,文献[8]则基于相同标准提出了RapidM DRC算法以适应速率更高的短波Autobaud波形[9]。文献[10]提出了一种快速DRC算法,通过收集包括误码率和信噪比在内的统计信息,结合当前误码率(Bit Error Ratio, BER)进行多个信息的统一决策,对数据速率进行调整。
文献[11]将原始STANAG 5066标准中的DRC算法和Trinder DRC算法进行改进,在改变数据速率之前增加了误码率判断模块,减少了数据速率的振荡,提高了链路连通率(Link Availability, LA)。
综上所述,学者们针对变速率通信取得了大量的优异成果,但目前DRC算法的研究主要集中在调制方式[12]和波形[13]上进行改善,因算法复杂度较高造成的调整时延也较长[14]。同时,在现役的短波电台中均采用了变速率通信技术[15],因此基于帧长的变速率算法是一个值得研究的方向。
1 传统的变速率算法
1.1 算法原理
1.1.1 Trinder DRC 算法
Trinder DRC算法的提出主要是服务STANAG 5066标准。针对该标准提出了三种不同的信道模型,包括AWGN (Additive White Gaussian Noise)、ITU-R(International
Telecommunication Union-Radio communications sector) Good和ITU-R Poor,参考接收端信噪比(Signal-to-Noise Ratio, SNR)的值来选择当前最优的数据速率,如表1所示。
通过表1获得初始传输速率后便进行传输,并计算误帧率FER,计算公式为:
FER=1-(1-BER)L
(1)
得到误帧率后对照表2改变传输速率:当误帧率达到最低门限时将数据速率降低一档(当前速率在75~2400bit/s时降低到当前值的一半);超过最高门限时将数据速率提高一档(当前速率在75~2400bit/s时提高一倍)。
1.1.2 RapidM DRC 算法
RapidM DRC算法的执行基于以下三个步骤:
步骤1 接收后计算信噪比,参照表1选择初始的数据传输速率;
步骤2 计算在当前速率下的误码率,根据表3判断是否需要改变速率;
步骤3 利用误码率和平均误码率计算最优的数据速率,得到数据速率后仅进行较小的数据速率变化。
同时算法实现安全控制,不允许将数据速率增加到两个以上级别(例如,如果当前数据速率为600bit/s,则新数据速率可能最多为3200bit/s),或将当前数据速率减小到三个以上级别。
1.2 算法仿真与分析
实现和分析DRC算法的仿真系统如图1所示,为了保证通信质量将信噪比门限设置为10-5,在AWGN、ITU-R Good和ITU-R Poor三种不同信道质量下进行仿真。
首先进行初始化过程,这个过程通过比较当前的SNR和SNR门限要求,计算初始数据速率。在初始化之后,通过式(1)~(3)计算BER和FER。
ΔSNR=SNRmeasured-SNRrequired
(2)
BER=10-5×10-ΔSNR
(3)
之后执行相应DRC算法,并更新数据速率。最后从以下几个指标[14]进行链路质量评估。
1)平均误码率BER 。
平均误码率表示误码率在时间上的平均,计算公式如下:
BER = ∑ N i=1 BERi×τi(BERi) ∑ N i=1 τi(BERi)
(4)
其中:Ti是时间间隔,N为时间间隔的总数;BERi表示第i个时间间隔中的误码率,当其大于10-3时系统进入截止状态;τi表示处于连通状态的时间间隔,计算公式如式(5)。
τi(BERi)= Ti, BERi≤10-30, BERi>10-3
(5)
2)平均误帧率FER 。
平均误帧率FER 的计算公式如下:
FER = ∑ N i=1 FERi×τi(BERi) ∑ N i=1 τi(BERi) ×100%
(6)
其中FERi为第i个时间间隔中的误帧率。
3)链路连通率LA。
LA用连通时间与总时间的比值表示,计算公式如下:
LA= ∑ N i=1 τi(BERi) ∑ N i=1 Ti ×100%
(7)
4)平均吞吐量Th 。
Th 的計算公式如下:
Th = ∑ N i=1 DRi×τi(BERi)×(1-BERi) ∑ N i=1 Ti
(8)
其中DRi表示第i个时间间隔的传输速率。
5)平均帧传输速率Gp 。
Gp = ∑ N i=1 DRi L ×τi(BERi)×(1-BERi) ∑ N i=1 Ti
(9)
其中L为第i个时间间隔的帧长。
本文列举了两种算法在信噪比时间降低(按正弦曲线)时,数据速率随信噪比SNR变化的情况,并分别在AWGN、ITU-R Good、ITU-R Poor三种不同信道质量下进行仿真。
在参数设置上,每次信道变化后的运行时间间隔Ti=120s;总运行时间间隔数N=100;帧长度L=240Byte。仿真结果如下:图2(a)为采用Trinder算法对信噪比向下变化和三个不同信道模型下的数据速率自适应情况,得到的链路评估指标如表4所示。该算法检测到的主要漏洞是数据速率的振荡导致链路截止状态(BER ≥10-3),降低了链路可用性。
得到的误码率值如图3(a)所示,可以看到数据速率振荡与10-3以上的误码率值重合。
图2(b)为采用RapidM算法对信噪比向下变化和三个考虑通道的数据速率自适应情况,得到的链路评价指标如表4所示。从表4中可以看出,RapidM算法的性能优于Trinder算法;然而它仍然存在误码率突然升高导致的数据速率震荡,如图3(b)所示。
2 基于自适应帧长的变速率传输算法
2.1 自适应帧长算法
信道能够容纳的帧长存在一个最佳值,但是很难精确地得到,目前只能够通过恰当的算法去逼近;同时要求算法要能够快速确定帧长,并且保证所用帧长的稳定性。
算法具体步骤如下:
1)首先发送端与接收端协商初始帧长度,发送端可以采用先验值的方法,通过侦听当前信道中发送成功的帧来确定初始帧长或者使用原来发送成功的帧长值。
2)发送端记录每次发送成功的帧长,当连续两个成功发送的帧长均为L时,以两倍L作为新的帧长进行发送;当达到预先规定的上限值时,帧的长度不再增加。
3)当某帧纠错失败需要重传时,将原帧重传两次,如果这两次传输均失败,则选择发送失败帧长度的一半作为新的帧长。当数据帧部分小于一个字节时宣告链路失效。
4)当出现帧长度连续在L和2L两个值之间跳动3次以后,以1.5L(长度取整数值)作为新的帧长进行发送。如果出现连续三次传输失败后将帧长降为L。
该算法是一个整体,既包含了遇阻时的快速避退,又包含了在信道质量优良情况下的充分利用,同时也避免了帧长在某一值附近震荡的发生。
2.2 传输算法模型
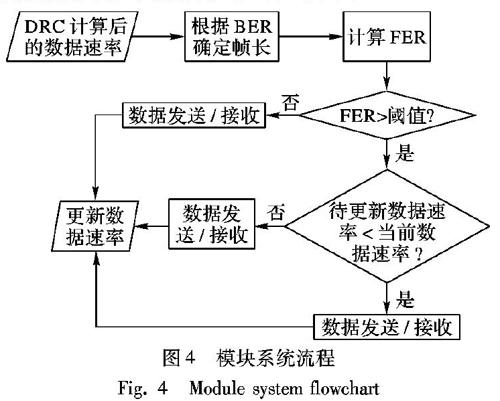
为解决Trinder DRC算法和RapidM DRC算法产生的速率震荡问题,在传统DRC算法流程中
执行DRC算法和更新数据速率两个步骤中间添加一个新的模块,模块具体流程如图4所示。
在DRC算法计算得到待更新的数据速率后,通过当前信道状态计算更新数据速率后的误码率,在更新数据速率前根据误更新速率后的误码率计算误帧率:如果误帧率大于阈值则不
更新数据速率;如果大于阈值、且待更新数据速率小于当前数
据速率,则降低速率;否则保持原有数据速率继续进行通信。
2.3 实验仿真与分析
本节主要通过仿真实验对Trinder算法和RapidM算法进行分析。
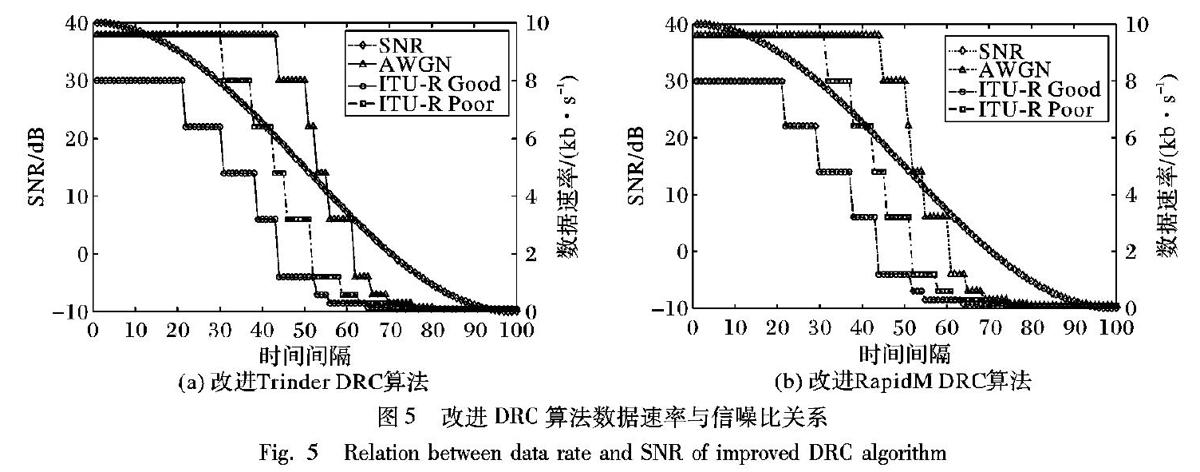
短波信道的状态变化比较快,具有一定的周期性,根据通信的经验值设置初始帧长度L=240Byte;保证通信质量的情况下设置FER阈值=10%;同样取信道变化后的运行时间间隔Ti=120s;总时间间隔数N=100,仿真结果如图4、5所示。
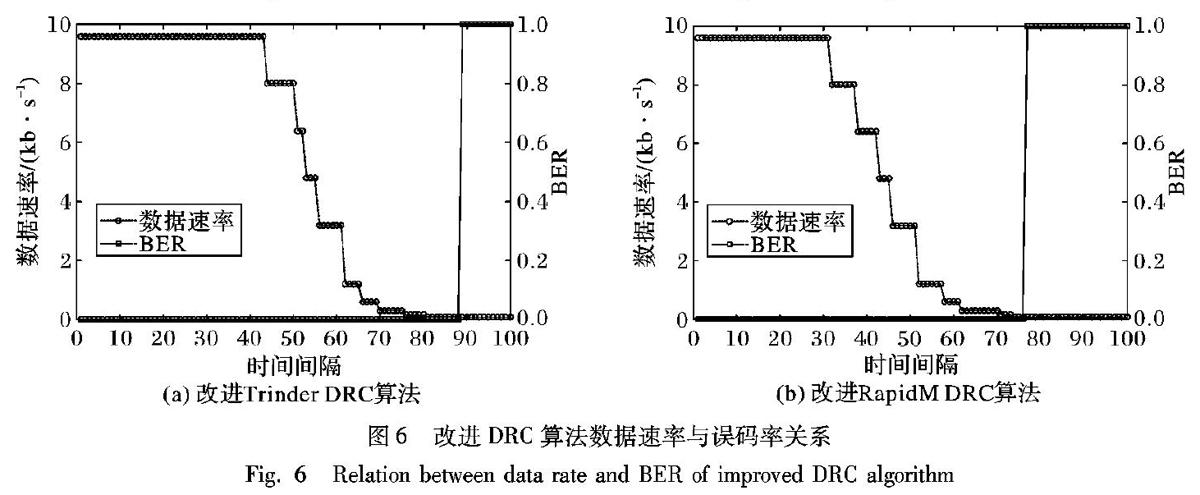
通过图4和图5可以看出,该算法基本消除了传统DRC通信系统的振荡。当最佳通信速率接近两个速率档的中间值时,传统的DRC算法会出现速率在两档上振荡。在改进后的算法中可以通过添加的判断模块来大幅减少速率振荡情况的出现。通过对比图3和图5可以看出,在误码率上也得到了大幅度优化,具体的链路质量如表5所示。
从表5中可以看出,改进后的Trinder算法和RapidM算法在性能上有一定提升,采用改进算法后Trinder算法误帧率降低了4.95个百分点,链路连通率提高了12个百分点;在RapidM改进算法中,误帧率降低了3.18个百分点,链路连通率提高了11个百分点,平均吞吐量和平均帧传输速率也有所提高。
综合上述实验结果可知,本文提出的基于自适应帧长的DRC算法与传统的两种DRC算法相比具有较大的优势,由此可见通过改变帧长来控制传输质量机制的有效性。因为传统DRC算法是在帧长不变的情况下进行评估的,当误码率增加时,帧长应该适当减小,以保持误帧率值不变,所以提高了通信质量。
3 结语
短波通信一直作為军事远距离通信的保底手段,由于短波信道质量变化较快,研究短波DRC算法具有重要的意义。
本文首先介绍了Trinder DRC和RapidM DRC两种传统的短波变速率算法,并进行了仿真,从仿真结果可以得出传统算法有速率震荡、误码率高的问题。同时提出了解决方案,通过在原有算法流程更新数据速率前加入新的判断模块,解决速率震荡的问题,并通过引入自适应帧长的概念降低了误帧率,提高了链路连通率。
后续研究将在以下两个方向进行延伸:1)实现更加高效的自适应帧长算法;2)结合宽带短波通信进行研究。
参考文献
[1] WANG J, DING G, WANG H. HF Communications: past, present, and future [J]. China Communications, 2018, 15(9): 1-9.
[2] 李木胜.短波通信组网发展趋势探究[J]. 无线互联科技, 2018(7):9-10. (LI M S. Research on the development trend of shortwave communication network [J]. Wireless Internet Technology, 2018(7):9-10.)
[3] 李德平.浅谈提高短波通信质量的方法[J].通讯世界,2015(2):11-12. (LI D P. On the methods of improving the quality of short-wave communication [J]. Telecom World, 2015(2): 11-12.)
[4] DING G, WANG J, WU Q, et al. On the limits of predictability in real-world radio spectrum state dynamics: from entropy theory to 5G spectrum sharing [J]. IEEE Communications Magazine, 2015, 53(7): 178-183.
[5] KOSKI E, WESTON J. Efficient high-fidelity simulation of HF communications systems and networks [C]// Proceedings of the 2015 IEEE Military Communications Conference. Piscataway, NJ: IEEE, 2015:1460-1466.
[6] SALOUS S, SHEARMAN E D R. Wideband measurements of coherence over an HF skywave link and implication for spread-spectrum communication [J]. Radio Science, 1986, 21(3): 463-472.
[7] TRINDER S E, GILLESPIE F R. Optimisation of the STANAG 5066 ARQ protocol to support high data rate HF communications [C]// Proceedings of the 2001 Communications for Network-Centric Operations: Creating the Information Force. Piscataway, NJ: IEEE, 2001: 482-486.
[8] SCHULZE S, HANCKE G P. Design and implementation of a STANAG 5066 data rate change algorithm for high data rate autobaud waveforms [C]// Proceedings of the 8th WSEAS International Conference on Electronics, Hardware, Wireless and Optical Communication. New York: WSEAS, 2009: 96-107.
[9] SHANNON C E. A mathematical theory of communication [J]. The Bell System Technical Journal, 1948, 27(3): 379-423.
[10] 汤军,陈劲尧,白翔.STANAG 5066标准的速率自适应机制研究[J].通信技术,2011,44(7):138-140. (TANG J, CHEN J Y, BAI X. Study on data-rate control mechanism in STANG 5066[J]. Communications Technology, 2011, 44(7): 138-140)
[11] SEQUEIRA V, QUELUZ M P, RODRIGUES A, et al. Data rate change algorithms for efficient HF communications [C]// Proceedings of the 2018 IEEE International Conference on Military Communications and Information Systems. Piscataway, NJ: IEEE, 2018:1-7.
[12] EPSTEIN M R. Polarization of ionospherically propagated HF radio waves with applications to radio communication [J]. Radio Science, 1969, 4(1): 53-67.
[13] 龔威. 短波自适应数据传输系统中的关键技术研究[D].西安:西安电子科技大学,2018:22-24. (GONG W. Research on key technologies in shortwave adaptive data transmission system [D]. Xian: Xidian University, 2018: 22-24.)
[14] GOODMAN J, BALLARD J, SHARP E. A long-term investigation of the HF communication channel over middle and high latitude paths [J]. Radio Science, 1997, 32(4): 1705-1715.
[15] 庄乾波.短波电台自适应的实现[J].中国新通信,2015(14):122-122. (ZHUANG Q B. Implementation of short-wave radio self-adaption [J]. China New Communications, 2015(14): 122-122)
[16] GOODMAN J, BALLARD J, SHARP E. A long-term investigation of the HF communication channel over middle- and high-latitude paths [J]. Radio Science, 1997, 32(4): 1705-1715.
