阵列互耦误差FIR校正滤波器设计与FPGA实现

姚志成 吴智慧 杨剑 张盛魁

摘 要： 针对传统型FIR滤波器在高阶条件下运算速度变慢与耗费资源增多这一问题，提出一种基于分段卷积的高速高阶FIR滤波器设计方法，通过在频域并行处理的方式实现了数据的快速处理。首先，确定滤波器的设计阶数M并将其作为基准序列长度，对输入的数字信号进行M周期延时;然后，将原序列与延时序列分别作快速傅里叶变换（FFT）;其次，将变换后的频域结果分别与滤波器相乘后作快速傅里叶逆變换（IFFT）;最后，通过重叠保留的方法实现两路数据的拼接。理论分析与仿真测试表明，与基于查找表（LUT）的传统分布式方法相比，同等阶数下所提方法的寄存器资源节省了30%以上。在此基础上利用实验平台的实测数据进行验证，结果表明，与互耦误差校正前相比，校正后的幅度失配均方根小于1dB，相位失配均方根小于0.1rad，实验数据充分展示了该方法对互耦误差校正的有效性。

关键词：数字阵导引头;互耦误差;FIR滤波器;现场编程门阵列;快速傅立叶变换

中图分类号： TN911

文献标志码：A

FIR correction filter design and FPGA implementation for array mutual coupling error

YAO Zhicheng，WU Zhihui*，YANG Jian，ZHANG Shengkui

Rocket Force University of Engineering Missile Engineering college， Xian Shaanxi 710025， China

Abstract： Focusing on the issue that the traditional Finite Impulse Response （FIR） filter slows down operation speed and consumes more resources under high-order conditions， a high-speed and high-order FIR filter design method based on piecewise convolution was proposed. Faster data processing was realized by the method of parallel processing in the frequency domain. Firstly， the design order M of the filter was determined and used as the reference sequence length， and the input digital signal was subjected to M period delay. Secondly， the original sequence and the delay sequence were respectively subjected to Fast Fourier Transform （FFT）. Thirdly， the transformed sequences were respectively multiplied by the filter and then subjected to Inverse Fast Fourier Transform. Finally， the merging of the two way data was realized by the method of overlapping reservation. Theoretical analysis and simulation tests show that compared with the traditional distributed method based on Look Up Table （LUT）， more than 30% of register resources were saved under the same order by the proposed method. On this basis， the measured data of the experimental platform were used for verification. Experimental results show that compared with the result of uncorrected mutual coupling error， the square root of the corrected amplitude mismatch is less than 1dB and the root mean square of phase mismatch is less than 0.1rad. Experimental data fully demonstrate the effectiveness of the method for mutual coupling error correction.

Key words： digital array seeker; mutual coupling error; Finite Impulse Response （FIR） filter; Field-Programmable Gate Array （FPGA）; Fast Fourier Transform （FFT）

0 引言

数字阵列雷达作为当今雷达发展的重要组成部分，在远距离目标探测、跟踪以及定位上扮演着越来越重要的角色。相比传统雷达体制来说，数字阵列雷达拥有着数量庞大的天线阵列，能够灵活控制波束、有效提高信号增益[1]。

然而在实际系统中，会存在各种误差使得天线方向图的主波束方向产生偏差、宽度变窄以及零陷与副瓣抬高[2]等，导致数字阵列雷达对空间信号到达方向（Direction of Arrival， DOA）的估计产生较为严重的偏差，阵列的输出信干噪比（Signal-to-Interference plus Noise Ratio， SINR）降低。其中，数 字阵列阵元间不可避免的互耦误差给陣列信号处理带来的影响非常恶劣。对数字阵导引头来说，互耦误差将直接影响到测角算法对目标的定位以及后续的成像识别，因此在数字阵导引头的生产与日常维护中，对互耦误差的校正显得尤为重要。

作为互耦误差校正的关键，校正滤波器承担着对各个阵元互耦误差的校正作用。为解决滤波器阶数与硬件资源之间的矛盾，文献[3]通过理论推导与实验分析得出在均衡带宽内，叠加的固定相移对均衡效果没有影响。文献[4]设计了一系列对比性仿真分析，深入研究了影响均衡效果的原因，得出了均衡算法的最优应用设计，对工程应用具有理论参考价值。 文献[5]提出了一种基于傅里叶变换的通道均衡算法，通过实验发现该算法受到许多实际因素的影响导致算法性能的严重下降。文献[6]分析了逆傅里叶变换算法均衡性能不理想的原因，基于此提出在逆傅里叶变换之前先对频域抽样点进行优化设计的方法，使得均衡性能得到改善，同时其运算量也得到有效减少。文献[7]借鉴快速卷积的实现方法，提出了一种基于快速傅里叶变换（Fast Fourier Transform， FFT）的高速率均衡器实现方法，与时域方法相比，该方法在滤波器阶数大于32阶时能明显降低对乘法资源的损耗。

文献[8]提出了一种改进的离散傅里叶逆变换法（Inverse Discrete Fourier Transform，IDFT），成功地克服了带外噪声带来的影响。文献[9]为了克服带外噪声的影响，采用的是对带内幅度特性进行梯形扩展和对带内相位特性进行线性外推的方法。傅立叶变换法作为频域最小二乘拟合法的延伸，它最大的优点就是在工程上算法简单、易于实现，这也是多数数字阵列雷达均衡器设计实例选择该方法的原因。除了上述优点以外，对于傅立叶变换法而言，带外噪声会影响系数的截取，进而影响均衡器的设计与均衡结果，所以对于带外噪声的处理以及系数截取方式

这两方面仍需进一步研究。

根据上述研究，结合实际处理需求，本文采用分段卷积的方法对FIR（Finite Impulse Response）滤波器进行了优化设计，使其能够在滤波器输入为长序列时仍能实现快速计算。基于Xilinx Zynq-7000系列现场编程门阵列（Field-Programmable Gate Array， FPGA）板卡对FIR滤波器了进行硬件设计，利用测试文件对滤波器的功能进行了测试验证。最后利用实测数据对基于FIR滤波器的宽带互耦误差校正算法的校正效果进行了验证，实验结果表明本文设计的FIR滤波器能够满足系统对于误差校正的需求，也进一步验证了基于FIR滤波器的宽带互耦误差校正算法的有效性与实用性。

1 FIR滤波器的优化设计

1.1 FIR滤波器设计方案选择

随着数字技术的快速发展，现场可编程门阵列（FPGA）得到了迅速发展和普及，整个器件的集成度与功能的多样性以及器件可靠性都非常出色。目前基于FPGA的高速高阶FIR滤波器的设计主要有两种方式：分布式算法（Distributed Arithmetic， DA）以及快速傅里叶变换法。

1）分布式算法。

分布式算法是一种实现乘法与加法运算的算法。其主要原理如下：

一个FIR滤波器的时域表达形式为：

y （n）= ∑ N-1 n=0  h （n）× x （n）= h （0） x （0）+ h （1） x （1）+L+ h （N-1） x （n-1）

（1）

进一步假设 h （n）为已知常数，而 x （n）为输入变量。对于有符号DA系统中假设变量 x （n）的表达式为：

x （n）=-2B· x B（n）+∑ B-1 b=0  x b（n）·2b;  x b（n）∈[0，1]

（2）

式中： x b（n）代表的是 x （n）的第b位， x （n）代表信号 x 的第n个采样。将式（2）代入式（1）可得：

y （n）=∑ N-1 n=0  h （n）· { -2B· x B（n）+∑ B-1 b=0  x b（n）·2b }

（3）

重新分别求和，可得：

y （n）= -2B·∑ N-1 n=0  h （n）· x B（n）+∑ B-1 b=0 2b·∑ N-1 n=0  h （n）· x b（n）

（4）

对于∑ B-1 b=0 2b·∑ N-1 n=0  h （n）· x b（n）的硬件实现，就是使用一个查找表（Look Up Table， LUT）实现映射，并提前设定程序的LUT接收一个N位输入向量：

x b（n）=[xb（0），xb（1），…，xb（N-1）]

（5）

输出为：

h （n）· x b（n）= [h（0）·xb（0），h（1）·xb（1），…，h（N-1）·xb（N-1）]

（6）

输出由相应的二次幂加权并累加，得到最终结果。

2）FFT法。

在频域实现FIR滤波器便是利用时域上的卷积等效于频域上相乘的原理。

y （n）=  x （n） h （n）=IFFT{FFT[ x （n）]×FFT[ h （n）]}

（7）

在实际系统中，滤波器的输入序列为有限长序列。假设两个有限长序列 x （n）与 h （n）的长度分别为N与M，将两序列进行补零操作使得两序列长度均为L（L=N+M-1）：

x ′（n）=  x （n），   0≤n≤N-10， N≤n≤L-1

（8）

h ′（n）=  h （n），   0≤n≤M-10， M≤n≤L-1

（9）

獲得了两个长度为L的序列后，利用循环卷积代替线性卷积：

y L（n）= x （n） h （n）= y C（n）= x ′（n） h ′（n）

（10）

式中，与分别表示线性卷积与循环卷积。

利用FFT计算 y L（n）的步骤为：

1）对 x ′（n）做L点DFT得到 X ′（k）;

2）对 h ′（n）做L点DFT得到 H ′（k）;

3）计算 Y （k）= X ′（k） H ′（k）;

4）对 Y （k）做L点IDFT得到 y L（n）。

3）方案比较分析。

数字阵导引头系统各阵元通道接收数据带宽较宽，基带信号采样率较高，数字正交解调后的I/Q两路信号的数据量较大，因此对于滤波器的处理速度有较高的要求。除此之外，为了保证信号校正的精度，需要设计较高阶数的滤波器进行校正。综上所述，校正滤波器对于阶数与处理速度均有较高的要求。

基于FFT的FIR滤波器的频域方法与时域方法相比减少了大量的运算量，并且滤波阶数越高其速度提高得更为明显。与基于分布式算法的FIR滤波器相比，同等阶数下基于FFT的FIR滤波器的处理速度更快，但资源消耗得更多。随着未来数字技术的发展，硬件资源的集成度将越来越高，同等阶数下基于FFT的FIR滤波器在处理速度上将越来越占有优势[10]。

综上所述，选择基于FFT的FIR滤波器作为数字阵导引头校正滤波器的设计方案。

2 基于分段卷积的FIR滤波器优化设计

在实际数字阵导引头互耦误差校正中，通常滤波器处理的序列 x （n）的序列长度较长。如果利用有限长序列进行卷积处理，快速傅里叶变换（FFT）与快速傅里叶逆变换（Inverse Fast Fourier Transform，IFFT）点数会很大，给硬件造成较大的负担;并且硬件的处理能力有限，并不能完成对于过长序列的FFT与IFFT;除此之外， h （n）还需要补较多的零。因此使用分段卷积的方式进行处理。

分段卷积是将 x （n）分成与 h （n）点数相仿的序列，分别使用FFT的方法得到每段的卷积结果，然后按一定的方式将序列接合在一起以最终得到总的输出序列。分段卷积主要有两种方法：重叠相加法与重叠保留法。

2.1 设计方法分析

1）重叠相加法。

重叠相加法需要将 x （n）分为若干个点数为N的序列 x m（n），并且将序列 x m（n）与M点序列 h （n）补零至点数为N+M-1，再进行 N+M-1点的FFT。通过观察，各分段卷积结果有重叠，需将重叠的部分相加得到最终的结果。整个方法需要对 x m（n）与 h （n）均进行补零，且FFT的点数较多，在实际FPGA实现中浪费了较多时间在补零上[11]。

2）重叠保留法。

重叠保留法需要将 x （n）分成若干个点数为N的序列 x m（n），保证前后两个序列有M-1个点是重叠的，将 h （n）补零至点数为N，并对两序列进行M点FFT。最后保留各段卷积后结果的后 N+M-1个样本，构成最终的序列。重叠保留法与重叠相加法的本质结果是相同的，但是重叠保留法的运算过程不需要对输入序列进行过多的补零操作，并且序列 h （n）可以提前进行补零以及FFT操作进而存入ROM中，因此选择重叠保留法进行分段卷积。

2.2 基于重叠保留法的校正滤波器优化设计

重叠保留法的具体原理如下：首先将 x （n）进行分段，使前后两序列中有M-1个点的重叠部分， x m（n）表示将 x （n）分段后的第m部分：

x m（n）= x （n+m（N-M+1））; 0≤n≤N-1

（11）

其长度为N，此时M≤N。对 h （n）进行补零操作得到 h ′（n），使得序列长度为M。利用循环卷积得到序列 h ′（n）与 x m（n）的卷积结果：

y ′m（n）= x m（n） h ′（n）

（12）

舍弃 y ′m（n）的前M-1个样本，保留剩下的N+M-1个样本，得到：

y m（n）=

0，    0≤n≤M-2

y ′m（n）， M-1≤n≤N-1

（13）

将 y m（n）拼接起来，得到 x （n）与 h （n）的线性卷积 y L（n）。

由上可知，单线程的卷积使得整个信号处理的效率较低，难以实现整个模块的快速操作，并且重叠保留法需要对长序列进行特殊的分段。因此结合实际设计一种基于重叠保留法的校正滤波器。具体步骤如下：

1）确定滤波器 h （n）的阶数为M，即序列长度为M，针对输入的数据序列 x （n），对其进行延时M个周期得到 x （n-M+1）;

2）对 x （n）与 x （n-M+1）两序列进行均匀分段得到 x m（n）与 x m（n-M+1），每段长度为N点满足N=2（M-1）且N为2的乘幂;对两序列分别做FFT，得到 X ′m（k）与 X ″m（k）（k=0，1，…，N-1）;

3）对 h （n）进行补零操作得到 h ′（n），其点数为N，做FFT得到 H ′（k）;

4）分别将 X ′m（k）与 X ″m（k）于 H ′（k）做乘积，继而做IFFT，得到N点的序列 y ′m（n）与 y ″m（n）;

5）分别取 X ′m（k）的与 X ″m（k）的后M-1个点，拼接成完整的N点的输出序列 y L（n）。

通過对上述步骤分析可知， x （n）延时后得到 x （n-M+1），两序列再进行分段，此时两序列之间相差M-1个时钟。在实际FPGA中，数据是按时钟输入的，所以 x m（n）与 x m+1（n）之间相差M-1个时钟。对于重叠保留法，每个子序列经过循环卷积舍弃前M-1个数据，并保留剩余M-1个数据作为最终线性卷积的结果。当 x m（n）与 x m（n-M+1）两序列同时输入进行FFT与IFFT后，分别经过重叠保留的操作，再进行拼接得到的序列等于常规方法中前两个序列重叠保留后的序列。

两路数据并行处理相比一路数据处理来说大大缩短了数据处理的时间，两路输出可以无缝拼接为完整的输出，不需要浪费多余的RAM对输出数据进行延时拼接，并且该设计流程能够充分发挥FPGA中FFT IP核Pipelined Streaming I/O结构在数据处理上的优势[12]，再加上分段卷积的方式在高阶高速校正滤波器上比其他方式拥有明显优势，所以这一优化设计能够较好地满足校正滤波器的设计需求。

3 基于FPGA的FIR滤波器设计与实现

3.1 校正滤波器总体设计框架

本节基于Xilinx Zynq-7000系列 XA7Z020CLG484设计一款64阶FIR滤波器[13-14]。根据2.2节中所提的设计方法，首先将信号分为两路并对其中一路信号进行延时63周期，将输入数据进行分段，每段长度均为128点，分别做FFT，得到对应的频域输出;其次从ROM中读取提前存入的滤波器系数，并将两路频域输出与存储在ROM中的FIR滤波器频域数据进行相乘（乘法器输出也是用过流水实现的）;经过上述两步后经过IFFT处理模块，只保留原始输出信号的后63点与延时后输出信号的65点，共同组成最终输出的128点，得到完整的线性卷积结果，进而可以实现待校正数据在校正滤波器中的流水线操作。具体设计如图3所示。

其中：

data_delay模块：通过调用RAM IP核实现对输入数据x_data的读写，进而对x_data进行延时处理;

fft_top_xfft模块：通过调用FFT IP核实现对输入数据x_data的FFT;

fft_top_x63fft模块：通过调用FFT IP核实现对输入数据x_63data的FFT;

fft_result_multiple模块：调用事先存入ROM的hfft_real_data与hfft_imag_data，并且通过调用Complex Multiplier IP核，实现对数据的频域相乘;

fft_top_xifft模块：通过调用FFT IP核实现对xfftXhfft_data_imag与xfftXhfft_data_real的IFFT;

fft_top_x63ifft模块：通过调用FFT IP核实现对x63fftXhfft_data_imag与x63fftXhfft_data_real的IFFT;

chongdie_out模块：通过调用RAM IP核实现对数据的缓存，进而实现对输出序列的保留与拼接。

3.2 FFT/IFFT模块设计

该设计利用Xilinx FFT IP核实现各模块的FFT/IFFT功能，FFT IP核可以支持点数较大的FFT运算，FFT内核可以实现N点DFT或IDFT计算，其中N=2m（m=3，4，…，16）。FFT内核有四种可选择的结构：Pipelined Streaming I/O、Radix-4 Burst I/O、Radix-2 Burst I/O以及Radix-2 Lite Burst I/O，其中Pipelined Streaming I/O结构允许连续对输入数据进行变换。

本设计的四个模块中128点的FFT/IFFT均采用Pipelined Streaming I/O结构实现。Pipelined Streaming I/O结构利用多个基2蝶形运算处理单元级联的方式实现对连续数据的处理。每个处理单元都有自己的存储模块用于存储输入数据和中间运算数据（如图4所示）。FFT IP核可以在执行当前帧数据运算的同时读取下一帧的数据，并输出上一帧数据运算的结果。这种架构也可以单独计算一帧的数据或者计算间断的数据输入。输入数据是以顺序的方式输入到FFT IP核中，而数据输出可采用顺序输出或者是倒序输出。在选择顺序输出的时候，会占用更多的存储器资源[15]。根据上述分析对Xilinx FFT IP核进行配置，如图5所示。

上述四个模块中，fft_top_xfft与fft_top_x63fft模块实现的是对输入数据的FFT，而fft_top_xifft与fft_top_x63ifft实现的是对输入数据的IFFT，在FFT IP核的配置过程中，利用模块中的输入fft_or_ifft对FFT IP核进行配置实现响应的功能。

3.3 频域相乘模块设计

在整个结构中fft_result_multiple模块的作用是从滤波器系数存储器中读取滤波器系数并与FFT的输出相乘，得到频域相乘的结果。频域相乘模块包括地址控制单元与复数乘法器两部分。其中核心复数乘法器主要利用了Xilinx中的Complex Multiplier IP核实现复数的相乘的功能，具体IP核的配置如图6所示。

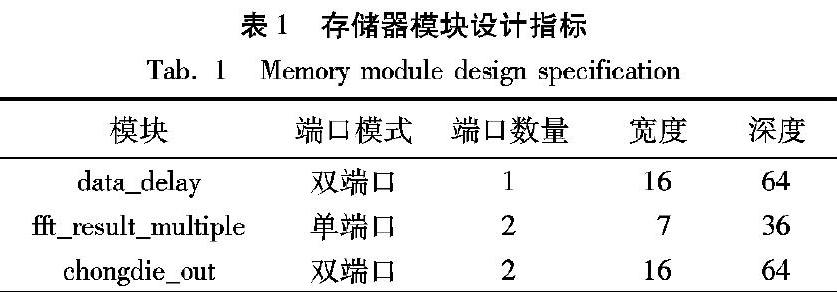
3.4 存储模块设计

在整体设计中，存储器模块的主要作用是利用ROM存储滤波器系数和利用RAM实现了对输入数据的延时以及利用RAM完成数据的缓存以及读取进而实现两路输出数据的重叠保留。

存储器模块是采用XA7Z020CLG484片内的嵌入式Block

RAM模块组成的单口RAM存储器。本设计采用Xilinx提供

的Block Memory Generator IP核对存储器模块进行设计。其

中data_delay模块、fft_result_multiple模块和chongdie_out模

块的设计指标如表1所示。

3.5 仿真验证及分析

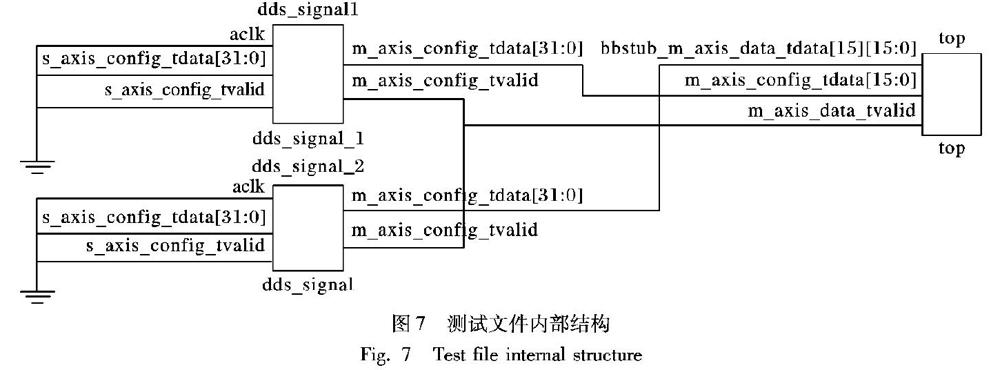
为进一步验证FIR滤波器的设计效果，本节基于上述设计的滤波器，设计了测试文件对滤波器的滤波效果进行测试，测试文件内部结构如图7所示。测试文件利用DDS Complier IP核构成两个模块dds_signal1和dds_signal2分别生成10MHz与80MHz的单频信号，信号采样频率为640MHz，然后将两路信号合成一路作为输入送入设计的FIR滤波器top模块中。在此基础上，利用Matlab中Filter Designer生成64阶截止频率为64MHz的低通滤波器，并将滤波器系数存入hfft_imag和hfft_real中。最后在VIVADO软件中利用测试文件进行功能测试。

测试结果表明所设计的滤波器可以将输入数据的高频部分剔除出去，只保留低频部分的单频信号。在64MHz工作时钟下，FIR滤波器完成运算只需要1ms左右，可以满足对滤波器速度的要求。

对于该设计，通过编译得到资源占用情况如图8所示。

为了比较本文算法与传统分布式算法在硬件资源的消耗上的差别，同样在Xilinx ZYNQ-7000芯片上实现64阶滤波器，对比分析结果如表2所示。

分析表2可知，基于分段卷积的并行算法与传统分布式算法相比，其寄存器、LUT（Look-Up-Table）和DSP（Digital Signal Processor）等资源占用率都得到明显降低，这是由于采用了分段卷积的方法实现高阶FIR滤波器可以有效减少运算部件的数量。

4 校正效果测试

4.1 实验设计

本文针对校正滤波器阶数较高、处理序列较长的特点，采用第2章中的设计方法对FIR滤波器进行设计。为了进一步验证校正滤波器对于误差校正的效果，利用八阵元数字阵列接收系统实验平台得到各通道的頻域特性，进而对校正滤波器的校正效果进行验证。由于阵列接收到的采样信号中包括多种误差的影响，其中最主要的便是幅相误差与互耦误差。为了验证宽带互耦误差校正方法的性能以及本文设计的FIR滤波器的校正效果，利用文献[6]中的宽带幅相误差校正方法对阵列接收数据幅相误差进行了校正。经过宽带幅相误差校正后的数据中主要包含互耦误差，进而消除了幅相误差对实验的影响。

本文利用八阵元数字阵列接收系统实验平台，通过该平台获取实验数据验证校正滤波器的校正效果。平台框架如图9所示。该系统的接收天线为八阵元均匀线阵，接收天线可工作频段为0.6～3.0GHz，具有窄带和宽带两种模式，窄带瞬时带宽为8MHz，宽带瞬时带宽为500MHz。数字接收组件由高速ADC（Analog-to-Digital-Converter）、高性能FPGA组成。

具体实验步骤如下：

1）将实验系统调整为校正模式，利用暗室中设置的信号源生成带宽为500MHz、中心频点为2.7GHz的线性调频信号射向阵列，进而得到各通道频率响应;

2）利用宽带幅相误差校正方法对阵列各通道频率响应进行幅相误差校正进而得到仅含有互耦误差的阵列接收数据;

3）利用互耦误差校正算法得到校正滤波器矩阵，该矩阵由64个滤波器组成;

4）在得到了滤波器系数的基础上，将滤波器系数存入ROM中，利用FPGA分别对各个滤波器进行设计与实现;

5）将各通道接收数据输入相应滤波器中得到输出数据，并将对应通道的输出数据进行相加，最终得到校正后的完整通道频率特性。

4.2 实验结果与分析

为了便于观察宽带互耦误差校正方法的校正效果，本文以第一通道为参考，给出了其他通道相对于第一通道的幅度差与相位差。

由图10可知，未对互耦误差进行校正时，幅度起伏可达到8.4dB，各通道的相位特性随频率非线性变化，经过宽带幅相误差校正后的数据一致性较好;但是受互耦误差的影响，各通道特性存在较明显抖动。经过处理后，幅度起伏降低至3.5dB以下，各通道相位基本呈线性变化。由此可见，宽带互耦误差校正算法是有效的。

为了定量地描述阵列各通道间的一致性，定义第i个通道的失配特性为：

Di（f）= Ci（f） Cref（f） =ai（f）exp（ji（f））

（14）

式中，Ci（f）和Cref（f）分别为第i个通道和参考通道的频率响应。

幅度失配均方根和相位失配均方根定义如下：

Δai=  1 B ∫B/2-B/2 ai（f）- i（f） 2df

（15）

Δi=  1 B ∫B/2-B/2 i（f）- i（f） 2df

（16）

其中：B为带宽， i（f）和 i（f）分别表示理想条件下的幅频与相频特性。

以第一通道为参考，各通道的幅度与相位失配均方根如表3所示。未校正时，最大幅度失配达到了2.5dB，最大相位失配达0.32rad，并且各通道之间的幅相失配差异较大;经过基于FIR滤波器的宽带互耦误差校正方法校正后，幅度失配均方根小于1dB，相位失配均方根小于0.1rad。这充分说明了本文方法对于互耦误差校正的有效性。

5 结语

为了进一步将理论算法应用于实际工程中，本文设计了一种基于分段卷积的高速高阶FIR滤波器。首先分析了基于分布式算法与基于FFT法的FIR滤波器的设计方案，并比较了它们的优缺点，发现基于FFT法的FIR滤波器频域设计方案更适合系统对滤波器高速高阶的需求;然后结合实际处理需求，基于分段卷积的方法对FIR滤波器进行了优化设计，使其能够在滤波器输入为长序列时仍能实现快速计算;基于Xilinx Zynq-7000系列FPGA板卡对FIR滤波器进行设计，利用测试文件对滤波器的功能进行了测试验证，并利用实测数据对基于FIR滤波器的宽带互耦误差校正算法的校正效果进行了验证，实验结果表明本文设计的FIR滤波器能够满足系统对于误差校正的需求，也进一步验证了基于FIR滤波器的宽带互耦误差校正算法的有效性与实用性。

参考文献

[1] 陈曾平，张月，鲍庆龙.数字阵列雷达及其关键技术进展[J].国防科技大学学报，2010，32（6）：1-7. （CHEN Z P， ZHANG Y， BAO Q L. Advance in digital array radar and its key technologies [J]. Journal of National University of Defense Technology， 2010， 32（6）：1-7.）

[2] 李卫星，张月，陈曾平.一种宽带阵列幅相与互耦误差联合校正算法[J].航空学报，2016，37（3）：1025-1035. （LI W X， ZHANG Y， CHEN Z P. Wideband calibration algorithm for amplitude-phase and mutual coupling errors [J]. Acta Aeronautica et Astronautica Sinica， 2016， 37（3）：1025-1035.）

[3] 彭小亮，李荣锋.固定相移对自适应通道均衡性能影响的分析[J].空军预警学院学报，2004，18（2）：11-13. （PENG X L， LI R F. Analysis of effect of constant phase-shifting on adaptive channel equalization performance [J]. Journal of Air Force Radar Academy， 2004， 18（2）： 11-13.）

[4] 杨虔静.数字阵列雷达自适应通道均衡算法研究[D].西安：西安電子科技大学，2011：47-53. （YANG Q J. Research on adaptive channel equalization algorithm for digital array radar [D]. Xian： Xidian University， 2011： 47-53.）

[5] 王峰，傅有光，孟兵.基于傅里叶变换的雷达通道均衡算法性能分析及改进[J].电子学报，2006，34（9）：1677-1680. （WANG F， FU Y G， MENG B. Performance analysis and improvement of the equalization algorithm based on Fourier transform for radar channel [J]. Acta Electronica Sinica， 2006， 34（9）：1677-1680.）

[6] 徐明灿.一种改进的雷达通道均衡算法[J]. 科技视界，2012（2）：69-72. （XU M C. An improved algorithm of the radar channel equalization [J]. Science & Technology View， 2012（2）： 97-98.）

[7] 贾可新，柳桃荣，刘振华.一种宽带阵列通道均衡器设计[J].航天电子对抗，2013，29（6）：62-64. （JIA K X， LIU T R， LIU Z H. A design of wideband array channel equalizer [J]. Aerospace Electronic Warfare， 2013， 29（6）： 62-64.）

[8] 袁上策，何子述.改进的多通道系统频域信道均衡算法[J].雷达科学与技术，2014， 12（5）：517-521. （YUAN S C， HE Z S. An improved frequency-domain equalization algorithm in multi-channel system [J]. Radar Science & Technology， 2014， 12（5）： 517-521.）

[9] 张月，鲍庆龙，杨剑，等.宽带数字阵列雷达通道均衡方法的设计与实现[J].信号处理，2010，26（3）：453-457. （ZHANG Y， BAO Q L， YANG J， et al. Design and Implementation of channel equalization method for wideband digital array radar [J]. Signal Processing， 2010， 26（3）： 453-457.）

[10] 王宇峰.基于FFT的快速卷积算法的FPGA实现[D].哈尔滨：哈尔滨工业大学，2011：11-17. （WANG Y F. FPGA implementation of FFT-based fast convolution algorithm[D]. Harbin： Harbin Institute of Technology， 2011： 11-17.）

[11] 王法栋，刘宇.高阶数字滤波器分布式算法结构比较[J].声学技术，2009，28（3）：307-311. （WANG F D， LIU Y. Comparison between distributed arithmetic architectures of high-order digital filters [J]. Technical Acoustics， 2009， 28（3）： 307-311.）

[12] 李大习.基于FPGA的可配置FFT IP核实现研究[J].电子科技，2014， 27（6）：46-49， 53. （LI D X. Research on and implementation of reconfigurable FFT IP core based on FPGA [J]. Electronic Science & Technology， 2014， 27（6）： 46-49， 53.）

[13] 張震. 基于FPGA的通用型FIR数字滤波器的研究与设计[J]. 软件， 2015， 36（6）：125-128. （ZHANG Z. Research and design of universal FIR digital filter based on FPGA[J]. Computer Engineering & Software， 2015， 36（6）： 125-128.）

[14] 卢雍卿， 李剑文， 许雯雯. 基于FPGA的数字滤波器设计与仿真[J]. 软件导刊， 2017， 16（2）： 85-88. （LU Y Q， LI J W， XU W W. Design and simulation of digital filter based on FPGA [J]. Software Guide， 2017， 16（2）： 85-88.）

[15] 钱慧玲，左明鑫，黄红星，等.基于FPGA的数字滤波器设计[J].大众科技，2010（10）：65-66. （QIAN H L， ZUO M X， HUANG H X， et al. Digital filter design based on FPGA [J]. Dazhong Keji， 2010（10）： 65-66.）