基于三元多臂赌博机的树结构最优动作识别

刘郭庆 王婕婷 胡治国 钱宇华

摘 要：蒙特卡羅树搜索（MCTS）在棋类博弈问题中展现出卓越的性能，但目前多数研究仅考虑胜负两种反馈从而假设博弈结果服从伯努利分布，然而这种设定忽略了常出现的平局结果，导致不能准确地评估盘面状态甚至错失最优动作。针对这个问题，首先构建了基于三元分布的多臂赌博机（TMAB）模型并提出了最优臂确认算法TBBA;然后，将TBBA算法应用到三元极大极小采样树（TMST）中，提出了简单迭代TBBA算法的TBBA_tree算法和通过将树结构转化成TMAB的 三元极大极小采样树 TMST最优动作识别（TTBA）算法。在实验部分，建立了两个精度不同的摇臂空间并在其基础上构造了多个具有对比性的TMAB和TMST。实验结果表明，相比均匀采样算法，TBBA算法准确率保持稳步上升且部分能达到100%，TBBA算法准确率基本保持在80%以上且具有良好的泛化性和稳定性，不会出现异常值和波动区间。

关键词：蒙特卡罗树搜索;三元多臂赌博机;最优臂确认;序列决策;纯探索

中图分类号： TP181

文献标志码：A

Best action identification of tree structure based on ternary multi-arm bandit

LIU Guoqing1，2，3， WANG Jieting1，2，3， HU Zhiguo1，2，3， QIAN Yuhua1，2，3*

1.Research Institute of Big Data Science and Industry， Shanxi University， Taiyuan Shanxi 030006， China ;

2.Key Laboratory of Computational Intelligence and Chinese Information Processing of Ministry of Education （Shanxi University）， Taiyuan Shanxi 030006， China ;

3.School of Computer and Information Technology， Shanxi University， Taiyuan Shanxi 030006， China

Abstract： Monte Carlo Tree Search （MCTS） shows excellent performance in chess game problem. Most existing studies only consider the success and failure feedbacks and assum that the results follow the Bernoulli distribution. However， this setting ignores the usual result of draw， causing inaccurate assessment of the disk status and missing of optimal action. In order to solve this problem， Ternary Multi-Arm Bandit （TMAB） model was constructed and Best Arm identification of TMAB （TBBA） algorithm was proposed. Then， TBBA algorithm was applied to Ternary Minimax Sampling Tree （TMST）. Finally， TBBA_tree algorithm based on the simple iteration of TBBA and Best Action identification of TMST （TTBA） algorithm based on transforming the tree structure into TMAB were proposed. In the experiments， two arm spaces with different precision were established， and several comparative TMABs and TMSTs were constructed based on the two arm spaces. Experimental results show that compared to the accuracy of uniform sampling algorithm， the accuracy of TBBA algorithm keeps rising steadily and can reach 100% partially， and the accuracy of TBBA algorithm is basically more than 80% with good generalization and stability and without outliers or fluctuation ranges.

The best action identification methods of Monte carlo tree search （MCTS） showed excellent performance in chess game problem. Most existing studies only considered the successful and failing feedback， which means that results follow Bernoulli distribution. However， this setting ignored the usual result of draw， which led to inaccurate assessment of disk configuration and even made wrong choice. In order to solve this problem， ternary multi-arm bandit （TMAB） is constructed and TBBA algorithm is proposed， which used for identifying best arm. TBBA algorithm then applyied to the ternary minimax sampling tree （TMST）. TBBA_tree algorithm is proposed by iteratively using TBBA algorithm. TTBA algorithm is presented through transforming the tree structure into special TMAB for the purpose of best action identification. In the experimental part， two arm spaces are established， several comparative TMABs and TMSTs are constructed. Experimental results showed that， compared to the uniform sampling algorithm， the accuracy of TBBA algorithm keeps rising steadily and can reach 100% in part. The accuracy of the TTBA algorithm is basically maintained more than 80%. Good generalization， stability also showed in TTBA algorithm.

Key words： Monte Carlo Tree Search （MCTS）; Ternary Multi-Arm Bandit （TMAB）; Best Arm Identification （BAI）; sequential decision-making; pure exploration

0 引言

AlphaGo、AlphaZero算法[1-3]的出现对人工智能领域产生了巨大的影响，算法面向两名玩家、完全信息、零和博弈的最优动作识别问题，并在围棋、将棋和象棋领域取得了从白板状态起步战胜人类专业棋手的卓越成绩。现有研究将最优动作识别视为一个树搜索问题，树结构的每一个节点表示博弈过程的每一个信息完全已知的盘面，节点的出边表示当前盘面下的可行动作集合。树搜索旨在寻找当前节点下的最优出边。大多数博弈形成的树结构拥有极大的搜索空间，即使带有巧妙修剪过程的算法想要对树结构进行穷尽搜索也是完全不可能的。因此，将有限的计算资源进行合理高效的分配是当前工作的研究重点。

在AlphaGo及其后续算法中使用的蒙特卡罗树搜索（Monte Carlo Tree Search， MCTS）模型结合了树搜索的精确性和随机采样的一般性，从而能有效地提高算法性能，节省计算资源。基于MCTS模型的算法创新和理论研究都取得了极大的突破。其中，Garivier等[4]提出了一个基础树搜索结构，它针对两名棋手的两轮零和完全信息博弈过程，并与极大极小树搜索结构有着很高的相似性。在基础树搜索结构中，因为棋手双方为零和博弈关系，因此己方必须在考虑对手对立作用的基础上选择可行动作集中的最优动作。在已有研究中，算法假设博弈仅有输赢两种结果，然而在现实场景中，类似围棋、象棋的博弈游戏常常包含第三种结果：平局。当博弈游戏的盘面较小或者博弈双方的水平基本相当时有很大的概率出现平局结果，并且考虑平局结果有助于棋手更准确地估计博弈结果，有益于分析本身和对手的行为。因此本文在基础树搜索结构之上假设每个叶子节点服从一个三元分布，并构建了基于三元分布的两层极大极小采样树（Ternary Minimax Sampling Tree， TMST），它能够模拟博弈过程中出现的成功、平局、失败三种结果。本文还提出了三元极大极小采样树最优动作识别（Best Action identification of TMST， TTBA）算法，从而更准确地评估每个盘面的状态，选择最优的可行动作。

三元多臂赌博机（Ternary Multi-Arm Bandit， TMAB）的最优臂确认算法是一种解决极大极小采样树最优动作识别问题的有效算法，本文通过将树结构的每一对动作视为一个摇臂构建了特殊的多臂赌博机（Multi-Arm Bandit， MAB）模型。MAB是描述连续决策问题中探索与利用权衡关系的重要模型。探索 利用窘境可以描述为：对于多个奖赏未知的摇臂，为了在有限次数的连续选择后使累积反馈奖赏最大化，每一次选择时都面临着是坚持目前已知的最好对象，还是探索可能的更优对象的问题。近年来，MAB在网页搜索、广告推荐、多路通信、大数据等方面受到广泛关注。

MAB中的最优臂确认问题与累积奖赏最大化问题相比较而言，前者表示了一个纯探索过程，即在有限次数的选择过程中，智能体不关注累计奖赏值，仅识别候选臂集合中具有最优目标的摇臂。目前基于纯探索的最优臂识别（Best Arm Identification， BAI）问题得到了广泛的关注与深入的研究。BAI问题包括两个主要研究方向：1）在设定置信度的前提下最小化采样次数;2）设定实验轮数，旨在使得误差概率最小化。部分现有算法将每一个奖赏未知的摇臂视为一个參数未知的伯努利分布，但是奖赏也常常包含一种无偏向的反馈情况。如在路径规划问题中，为了简化人为设定奖赏值的工作量，除遇到障碍物或者接近目标等重要方向选择外，其他选择通常设定其奖赏为零。在游戏场景中，只有充分地估计玩家的输赢及平局的概率，才能挑选出最合适的对手或队友从而赢得游戏。因此，为了更加准确地模拟摇臂服从的分布，从而更高效地识别目标，本文设反馈结果包含三个类别：失败、平局和成功，并称此模型为三元多臂赌博机（TMAB）。

本文基于贝叶斯思想并利用共轭先验的属性解决TMAB最优臂确认问题，并提出了TMAB最优臂确认 （Best Arm identification of TMAB， TBBA）算法。本文提出的TBBA算法根据每个摇臂后验分布的采样值选择一个最具优势的摇臂作为采样臂并对其进行采样，这一方法利用了贝叶斯估计在选取当前最优臂的同时还能探索摇臂未知空间的优势。在贝叶斯推断中，如果后验分布与先验分布属于同类分布，则先验分布与后验分布被称为共轭分布，而先验分布被称为似然函数的共轭先验。TBBA算法利用狄利克雷分布和多项分布的共轭属性并基于共轭先验形成的先验链，实现算法运行过程中的相关参数更新。

本文的主要工作如下：

1）引入了无偏向反馈值概念，提出了一个基于贝叶斯思想和共轭分布先验链的TBBA算法，能够对本文构建的TMAB的最优臂进行有效确认;

2）将 TBBA算法应用到本文提出的极大极小采样树结构中，解决了两名玩家的两轮零和完全信息博弈下的最优动作识别问题;

3）建立了两个臂空间并在其基础上构造了多个具有对比性的三元多臂赌博机、三元极大极小采样树结构，验证了本文所提出的TBBA、TTBA算法能够有效地识别集合中的最优对象。

1 相关工作

多臂赌博机在多个领域中发挥着重要的作用，MCTS及相关模型在不同的背景下也都有着广泛的应用和重要的研究意义。接下来，本文将介绍部分多臂赌博机和贝叶斯推理的工作以及MCTS的相关研究。

1993年，Thompson[5]以临床实验问题为背景提出了多臂赌博机模型。在关于累积奖赏最大化的研究中，文献[6]介绍了两个极端的案例：独立同分布的奖赏和对抗性的奖赏，并给出了简洁的遗憾分析。算法还描述了有限动作的基本设定和赌博机模型一些重要的变体和扩展。同时，多臂赌博机的最优臂确认问题也取得了显著的成果。在设定置信度并使得采样次数最小化的研究方向中，已有文献提出了一致采样消除法、上下置信界法并就采样次数的上下界进行了深入的研究[7-13]。在设定实验轮数并使得误差概率最小化的前提下，现有研究在最优臂个数、策略思想、理论分析、应用领域等方面展开了研究。在关于最优臂个数研究中，文献[14]提出了单个最优臂确认的连续消除算法，随后文献[15]中提出了基于连续接受和拒绝思想的多个最优臂确认算法。

文献[16]针对连续消除算法提出了一个统一框架，并将设定的轮数根据一个与每轮存在臂集相关的非线性函数进行划分。在理论分析方面，通过引入Kullback-Leibler散度，文献[17]在原基础算法之上得到了更紧的上界，文献[18]中给出了更有效的下界。在文献[19]中，算法框架表明上述固定置信度和固定轮数的设定可以共用一个算法框架进行最优臂确认并给出了证明。

在策略思想方面，因为基于贝叶斯思想的汤普森采样通常被视为一个解决探索 利用平衡问题的启发式方法，因此它常被应用于多臂赌博机的研究中并展现出易实现性和优异性能[20]。为了能够保证更好的定向探索，文献[21]引入了乐观贝叶斯抽样（Optimistic Bayesian Sampling， OBS）算法，使得选取动作的概率与该动作值的不确定性成正比增加。在特殊的单轮多次采样多臂赌博机模型中，文献[22]也给出了多轮汤普森采样（Multiple-Play Thompson Sampling， MP-TS）算法并讨论了该算法的遗憾分析。

MCTS在包括棋类博弈的多个领域中展现了巨大的优势。文献[23]概述了其核心算法的推导过程，介绍了一些已经提出的变化和增强的结构，并总结了MCTS方法应用至关键游戏和非游戏领域的结果。文献[24]解释了MCTS的主要算法如何提高计算机围棋的技术水平。针对一次对弈的简化MCTS模型，文献[25]提出了基于伯努利分布的两种策略并讨论了这两种算法的样本复杂度和一个下界分析。在不限层数、基于伯努利分布的简化MCTS模型中，文献[25-26]提出了最优动作确认的算法及理论分析。

2 三元多臂赌博机的最优臂确认

本文通过贝叶斯思想对基于三元分布的多臂赌博机进行最优臂确认，提出了多臂赌博机最优臂确认（Best Arm Identification of Multi-Arm Bandit， MAB_BAI）问题的一般算法框架，描述了如何运用贝叶斯思想和共轭分布的先验链进行三元MAB_BAI的反馈值获取、采样臂选择、参数更新和算法最优臂输出。

2.1 基于三元分布的多臂赌博机

多臂赌博机是由K个摇臂组成的系统（如图1），臂集A中的每个摇臂a∈{1，2，…，K}服从一个参数未知的概率分布。现有研究多将臂分布建模为伯努利分布，本文为了更准确地模拟反馈结果将臂分布建模为三元分布，从而建立了三元多臂赌博机模型。其中，每一个摇臂a都服从一个三元分布，即每个臂拥有不同的三元概率值：  μ a=（μam）m∈{1，2，3}=（μa1，μa2，μa3），如表1所示，μa1、 μa2、 μa3分别代表臂a取值-1、0、1的概率或失败、平局、成功的概率，并且μa1+μa2+μa3=1。

在三元多臂赌博机中，本文将失败概率值最小的臂作为最优臂，若出现多个臂失败概率最小时，本文将平局概率最小的臂作为最优臂。即：

a*=arg min m=2 min m=1 （μam）; a∈{1，2，…，K}

（1）

在现有研究中，算法将具有最大期望值的臂作为最优臂。本文没有使用这种衡量指标，因为当出现如表2的两个摇臂时，若按照本文最优臂定义，臂2为最优臂;如果将期望值作为评判标准时，臂1是最优臂，然而臂1的失败概率更大，更容易陷入最差的结果中。

2.2 三元多臂赌博机的最优臂确认算法

本文考虑固定实验轮数下的多臂赌博机最优臂确认问题，基于此问题的算法框架通常包含如下过程：第t轮时，算法依据选臂策略从臂集A中选择一个采样臂At，然后对臂At按照概率值为 μ At的分布进行采样并得到一个反馈值 R t。算法再依据 R t对与其相关的臂进行更新，更新内容包括分布参数、采样次数或算法定义的相关变量。随着实验次数的增加，算法可以逐渐得到每个臂接近分布概率真实值 μ a的估计值   a。当算法运行至第t+1轮时，算法终止并返回具有最优概率估计值   的臂作为多臂赌博机的算法最优臂 。上述过程主要包括四个研究点：选择采样臂、获取反馈值、更新相关参数和输出算法最优臂。以下是它们在三元多臂赌博机中的具体实现。

1）反馈值的获取。

当算法运行至第t轮并按照选臂策略从臂集A中选择采样臂At后，再根据At的分布概率 μ At=（μAt1， μAt2， μAt3）进行采样并得到一个三元反馈值 R t=[r1，r2，r3]，其中ri∈{0，1}，∑ 3 i=1 ri=1。基于此，本文算法将反馈值 R t=[r1，r2，r3]的概率记为：

P（ R t |  μ At）=∏ 3 i=1 （μAti）ri

（2）

2）相关参数的更新。

首先，本文算法定义分布概率 μ a=（μa1，μa2，μa3）服从参数为 θ    ·   a=（θ   ·   a1，θ   ·   a2，θ   ·   a3）的狄利克雷分布，即对于每个臂a∈{1，2，…，K}，在第t轮时其先验分布为：

D（ θ    ·   at）= 1 B（ θ    ·   at）  ∏ 3 i=1 （μai）   at，i-1

（3）

其中，B函數是一个标准化函数，目的是使狄利克雷分布的概率密度积分等于1。

然后，算法将对臂采样后得到的反馈值视为贝叶斯估计中的似然函数，并与先验分布D（ θ    ·   Att）结合求出如下后验概率：

p （ θ Att |  R t）= p（ R t |  θ    ·   Att）p（ θ    ·   Att） p（ R t） ∝p（ R t |  θ    ·   Att）p（ θ    ·   Att）=

∏ 3 i=1 （μAti）ri×∏ 3 i=1 （μAti）   Att，i-1=

∏ 3 i=1 （μAti）ri+   Att，i-1

（4）

算法发现贝叶斯估计的后验分布可以视为参数为 θ Att= θ    ·   Att+ R t的狄利克雷分布，用B函数将它标准化就得到本文算法的后验分布为：

D（ θ Att）= 1 B（ θ Att） ∏ 3 i=1 （μAti） θ Att，i-1

（5）

上述过程中，后验分布与该先验分布为共轭分布，则基于共轭先验可以形成一个先验链：当前轮每个臂的后验分布可以作为下一轮的先验分布，即D（ θ    ·   at+1）=D（ θ at）。算法不断迭代使得基于分布参数的分布概率评估更加准确。在此迭代过程中：当算法运行到第t+1轮时，基于每个臂在第t轮的后验概率D（ θ at）挑选出采樣臂At+1后，对其进行采样并获得反馈值 R t+1;然后利用反馈值对D（ θ At+1t）的参数进行更新。根据前文可知 θ At+1t+1= θ At+1t+ R t，即参数更新只需要把反馈值 R t+1为1的第i个分量在采样臂参数 θ At+1t的对应分量加1就能得到第t+1轮的后验分布D（ θ At+1t+1），非采样臂的其他摇臂直接将第t轮的后验分布作为第t+1轮的后验分布。之后，算法可以继续重复上述参数更新过程直至算法运行结束。

3）采样臂的选择。

在算法运行到第t+1轮时，算法依据每个臂在第t轮的后验分布D（ θ at）进行随机采样并得到K个采样值 θ ′at+1，然后从K个采样值中选择出最具优势的臂：

At+1=arg min m=2 min m=1 （ θ ′at+1，m）

（6）

作为算法在第t+1轮的采样臂。通过对后验狄利克雷分布随机采样而选取的采样臂综合了摇臂的最优性和可探索性，在利用了摇臂现有信息的同时也对摇臂的不确定性进行了探索。

4）算法最优臂的获取。

当算法运行结束后，每个臂都服从参数为 θ aT的狄利克雷分布D（ θ aT）。通过狄利克雷分布的性质：  μ a=   θ a1  θ a1+ θ a2+ θ a3 ，  θ a2  θ a1+ θ a2+ θ a3 ，  θ a3  θ a1+ θ a2+ θ a3  ，算法可以得到每个摇臂的分布概率估计值：

a=

θ aT，1  θ aT，1+ θ aT，2+ θ aT，3 ，  θ aT，2  θ aT，1+ θ aT，2+ θ aT，3 ，  θ aT，3  θ aT，1+ θ aT，2+ θ aT，3

（7）

并在此基础上获得算法最优臂：

=arg min m=2 min m=1 （ am）

（8）

综上所述，三元多臂赌博机最优臂确认问题的具体流程如下：

算法1  三元多臂赌博机的最优臂确认（TBBA）算法。

输入  多臂赌博机臂集A，各臂分布概率 μ a，轮数T;

输出  算法最优臂。

程序前

1）

对每个臂设定参数初始值： θ a0=（1，1，1）

2）

Fo r t={1，2，…，T} do：

3）

Fo r a∈{1，2，…，K} do：

4）

进行随机采样：    at=D（ θ at-1）

5）

End For

6）

选择采样臂： At=arg min m=2 min m=1 （   at，m）

7）

对At根据分布概率 μ At=（μAt1，μAt2，μAt3）采样并得到反馈值：  R t=[r1，r2，r3]

8）

If  rm=1

then θAtt，m=θAtt，m+1，m∈{1，2，3}

9）

End If

10）

End For

11）

利用式（7）计算得到每个臂的分布概率近似值

12）

利用式（1）计算得到算法最优臂

程序后

算法运行之初，本文假设每个臂的先验分布是参数为 θ    ·   a1=（1，1，1）的狄利克雷分布D（ θ    ·   a1），为了便于组织算法流程框架，将其记为D（ θ a0）。接着重复伪代码中的流程直至第T轮时算法运行结束。本文通过每个臂在第T轮的后验分布D（ θ aT）得到算法最优臂并输出。

3 三元极大极小采样树最优动作识别

3.1 基于三元分布的极大极小采样树

以AlphaZero的模型框架——蒙特卡罗树搜索为背景，Kaufmann等[26]将一个两名玩家的两轮零和完全信息博弈过程进行简化并建立了一个树搜索结构，本文在此基础上重新建立叶子节点服从的分布，并定义新的树搜索结构为极大极小采样树如图2所示。它与常见的三层极大极小树搜索结构相比，相似之处包括：1）根节点为极大节点;2）第一层节点为极小节点，极大节点与极小节点交替出现;3）叶子节点为根节点的奖赏信息。不同之处在于：极大极小树中叶子节点表示已知固定的奖赏值，而極大极小采样树的每一个叶子节点是一个参数未知的三元分布。

极大极小采样树结构设定玩家A为根节点并且有K个可行动作，具有竞争关系的玩家B作为第一层节点（竞争关系指玩家A选择具有最大优势的动作，玩家B选择使A优势最小的动作）。对于玩家A的每一个可行动作组i∈{1，2，…，K}，玩家B有j∈{1，2，…， Ji}个可行动作。树结构的叶子节点是玩家A博弈结果的概率分布，本文假设第i组中第j个叶子节点服从概率值为 μ ij=（μijm）m∈{1，2，3}=（μij1，μij2，μij3）的三元分布vij，其中，μij1、 μij2、 μij3分别表示玩家A获得反馈值-1、0、1的概率，也可将其视为失败、平局、胜利的概率。

TMST最优动作识别算法的目标是在有限的轮数T内，识别出玩家A在可行动作集合中的最优动作i*。因为零和博弈过程中玩家A和B为竞争关系，因此，算法不能简单地从所有的叶子节点中选择最有优势的节点

i′j′=arg min m=2 min m=1 （μijm）;       i∈{1，2，…，K}且j∈{1，2，…， Ji}

（9）

后将i′作为玩家A的最优动作。玩家A的最优动作应该是在玩家B刻意降低玩家A博弈优势的情况下，A能得到的最优叶子节点i*j*中的动作，其定义为：

i*=arg min m=2 min m=1 （μij*im）; i∈{1，2，…，K}

（10）

其中对于每一个动作组i：

j*i=arg max m=2 max m=1 （μijm）; j∈{1，2，…， Ji}

（11）

3.2 TMST最优动作识别算法

根据上文极大极小采样树最优动作i*的定义，树结构可以被视为两层三元多臂赌博机组成的系统。基于此观点本文提出了基于三元极大极小采样树的TBBA算法（TBBA algorithm based on TMST， TBBA_tree），其主要思想是：先后在下层、上层使用TBBA算法，从而找到玩家A的算法最优动作i   ^   。算法的具体过程如下：1）划分树结构上下层的实验轮数。2）在下层中，玩家B在每一个动作组i∈{1，2，…，K}的Ji个动作中选择使玩家A的优势最小的动作j*i，这个部分可以视为一个目标与上文相反的三元多臂赌博机模型，此模型的最优臂是玩家A博弈结果最差的臂。树结构下层共有K个多臂赌博机，因此，算法得到K个最差臂。

3）在上层中，玩家A在这K个最差臂中选择最具优势的臂，此时，多臂赌博机模型与上文所述一致并且将这个部分视为第K+1个多臂赌博机。

4）将第K+1个多臂赌博机返回的摇臂作为树结构中玩家A的最优动作i*，算法过程如图3所示， 首先在每组内通过TBBA_tree算法找到最差臂j*1， j*2，…， j*K（分别标记为1，2，…，K），然后根据K个最差臂选择出整体最优臂j*K（深灰色），即玩家A的最优动作为K。

在TBBA_tree算法实验过程中可能存在以下问题：1）由于树结构被分成两层多臂赌博机，因此实验开始之前需要人为设定上下层各多臂赌博机的实验轮数，这将造成一定的人力开销;2）在多数情况下，相同的树结构、不同的实验轮数分配方式会产生不同的实验结果，因此，实验结果会存在很大的标准差，使得结果丢失评判价值;3）当实验轮数全部分配给下层时，极有可能造成实验结果中存在离群点。图4表示TBBA_tree算法在一个给定的树结构中出现上述2）、3）两个问题。

为了解决上述问题，本文基于文献[4]提出的方法将树结构整体视为一种特殊的三元多臂赌博机。这个特殊的多臂赌博机一共包含 =∑ K i=1 Ji个臂，每个臂p∈ 由一对动作对表示（如图5灰色部分所示），即：p=（i， j）。多臂赌博机的臂集为：P={（i， j）：1≤i≤K，1≤j≤Ji}。每个臂p服从参数为 μ p=（μpm）m∈{1，2，3}=（μp1，μp2，μp3）的三元分布νp。根据上述设定，极大极小采样树的最优动作确认问题转换成从包含 个臂的三元多臂赌博机中选择一个臂子集，臂子集中所有的臂都是第i组内玩家B的可行动作，且i符合玩家A最优动作的定义。

本文基于特殊三元多臂赌博机模型和TBBA算法提出了一个新的极大极小采样树的最优动作识别算法——TTBA。 算法具体过程如下：

算法2  三元极大极小采样树的最优动作识别（TTBA）。

输入  采样树结构Tree，各叶子节点的概率值 μ i， j，轮数T;

输出  算法确认的最优动作 。

程序前

1）

对臂集P={（i， j）：1≤i≤K，1≤j≤Ji}中的每一个臂p设定参数初始值： θ i， j0=（1，1，1）

2）

Fo r t=1，2，…，T do：

3）

Fo r i=1，2，…，K do

4）

Fo r j=1，2，…， Ji do

5）

进行随机采样：   i， jt～D（ θ i， jt-1）

6）

End for

7）

返回组内最差动作：Ji，t=arg max m=2 max m=1 （ i， jt，m）

8）

End for

9）

返回组间最优动作：

It=arg min m=2 min m=1 （ i， Ji，tt，m）

10）

对摇臂Pt=（It， JIt，t）进行采样并得到反馈值：    R t=[r1，r2，r3]

11）

If  rm=1 then  θ Ptt，m= θ Ptt，m+1，m∈{1，2，3}

12）

End if

13）

End for

14）

得到每个摇臂分布概率的近似值：

p=   θ pT，1  θ pT，1+ θ pT，2+ θ pT，3 ，  θ pT，2  θ pT，1+ θ pT，2+ θ pT，3 ，  θ pT，3  θ pT，1+ θ pT，2+ θ pT，3

15）

得到算法最优动作：

i   ^   =arg min m=2 min m=1 （ i，  im），i∈{1，2，…，K}

其中對于每一个动作i：

i=arg max m=2 max m=1 （ i， jm）， j∈{1，2，…， Ji}

程序后

与TBBA算法相同，本文假设每个臂的先验分布是参数为 θ    ·   i， j1=（1，1，1）的狄利克雷分布D（ θ i， j0）。接着重复伪代码中的流程，直到达到轮数T+1输出算法最优臂。算法过程如图5所示，将每一个的叶子节点视为一个摇臂，此时共有 =∑ K i=1 Ji个摇臂。根据TTBA算法从 个摇臂中选择出玩家A最优动作组内的叶子节点2.2（深灰色），即玩家A的最优动作为2。浅灰色图形表示一个动作对可视为一个三元多臂赌博机。

与TBBA_tree算法相比，TTBA算法既避免了出现由于人为划分实验轮数而导致的离群点和明显波动的实验结果，又表现出优异的性能。图6表示TTBA算法的实验结果，TTBA算法和TBBA_tree算法使用的树结构相同。

4 实验与结果分析

4.1 度量标准

本文提出的TBBA、TTBA算法的目标都是识别一个集合中最优对象，因此，本文将准确率作为算法的性能评估指标，其定义为：

ACCURACY=P（ =a*）= 1 R ∑ R r=1 1 r=a*

其中： 表示算法输出的对象，a*表示真实最优对象， r表示第r次运行结束时算法输出的对象，R表示算法运行的次数。与此同时，在三元多臂赌博机的测试中，为了更加清晰地观察算法的性能，本文定义了算法的得分：

GRADE=  1 R ∑ R r=1 （g（a*）-g（ r））=

1 R  R×g（a*）-∑ R r=1 g（ r）

其中：g（a*）、g（ r）分别表示真实最优对象的分数和算法在第r次运行结束时返回的对象 r的分数。

文献[11，25-26]等已经对多臂赌博机最优臂确认问题以及极大极小采样树最优动作识别问题展开了深入的研究，并提出了有效的算法。在实验部分验证算法性能时，先设定模型中的参数值，即每个摇臂或每个叶子节点的分布概率值;然后在给定的模型上运行算法，从而验证算法的性能。本文为了验证TBBA和TTBA算法的高效性、稳定性，建立了两个精度不同的臂空间：第一个臂空间设定每个臂服从概率值为 μ =（μ1，μ2，μ3）的三元分布，其中（μm）m∈{1，2，3}∈（0.1，0.2，…，0.9），并且μ1+μ2+μ3=1;第二个臂空间设定每个臂服从的三元分布概率值（μm）m∈{1，2，3}∈（0，0.05，…，1.0），并且μ1+μ2+μ3=1。然后在此基础上构建了多个参数给定的、具有比较性的三元多臂赌博机及三元极大极小采样树模型。其中，模型结构多样，覆盖范围广泛，并且摇臂和叶子节点的分布概率值在臂空间中随机选择保证了模型的随机性。本文设定不同精度的臂空间也有助于在较低的实验轮数内展现算法的性能，更能突显模型结构对算法的影响。

4.2 TBBA算法实验结果

本节实验以游戏过程中玩家选择队友为例。每个候选玩家的实力都由其赢局、输局、平局的概率表示，玩家的目标是选择出最具优势的候选玩家。本文根据问题性质将每个候选玩家视为一个服从三元分布的摇臂，将此问题建模成一个三元多臂赌博机，算法旨在确认出模型中的最优臂。每个候选玩家的分布概率取值具有随机性，因此，本文算法随机从臂空间中选择每个摇臂的分布概率值，这样可以保证实验结果的普适性。为了验证基于三元分布的多臂赌博机最优臂确认（TBBA）算法在三元多臂赌博机（TMAB）模型中的性能，本文将TBBA算法与均匀采样（Uniform sampling， U）算法进行比较，并设置了两组对比实验。 实验结果中，方块线表示TBBA算法，三角线表示U算法。

第一组实验验证TBBA算法在臂数相同、识别难度不同的三元多臂赌博机中的有效性。本文依据第二个臂空间建立了如表3所示的3个TMAB模型，其中每一个模型包含5个臂，按照摇臂的序号依次设置分数为5、4、3、2、1。不同模型臂间的识别难度逐渐增大。本文分别在三个模型上运行了TBBA算法和均匀采样算法，实验结果如图7所示，其中（a）表示算法的准确率，（b）表示算法运行结束后的得分。在模型1中，由于各臂分布概率值差距较大，因此算法在很少的轮数内通过估计各臂分布的失败概率就能确认出最优臂： =arg min m=1  μam。图7第一列展现出在摇臂容易区分的模型中TBBA算法比U算法的性能稍有优势，并且大约在400轮后两个算法性能都趋于稳定并能完全确认最优臂。模型2缩小了臂分布之间的间隔，模型中摇臂分辨难度被提高，图7第二列表明TBBA算法性能优良、提升速度更快。在模型3中，摇臂之间仅在平局概率有细微的差别。均匀采样算法的准确率在20%波动，得分约为300，这表明策略几乎无效，算法随机返回最优臂;而TBBA算法仍表现出良好的性能，算法的精确度随轮数增加呈现出稳定的增长趋势。实验结果表明：TBBA算法在不同分辨难度的TMAB中都具有良好的性能，尤其对于臂分布非常相似、确认难度很高的模型，TBBA算法的优势更加显著。

第二组实验验证TBBA算法在不同摇臂个数的三元多臂赌博机中的有效性，实验结果如图8所示。

图8（a）表示TBBA算法在基于臂空间一随机生成的分别包含5、10、20、30个摇臂的TMAB上的实验结果。在相同的实验轮数下，随着臂数的增加，算法的准确度有所下降。但是在相同臂数中，TBBA算法随着轮数的增加，性能逐步提升。当模型包含5、10个臂时，TBBA算法随着实验轮数的增加性能得到快速提升，并能保证稳定性。在20、30个臂的TMAB中，均匀采样方法丧失作用，但TBBA算法保持稳步高速提升的性能，在3000轮时，算法的准确率超过80%。图（b）表示TBBA算法在基于臂空间二中随机生成包含50、100、150、200个臂的TMAB上的实验结果。TBBA算法的性能随着轮数的增加保持上升的趋势。当臂数较小、轮数很少时，TBBA算法就具有很高的准确度;在臂数较大时，TBBA算法在短时间内性能能得到快速提升。

实验结果表明：TBBA算法在臂数不同的TMAB中，性能能保持稳定上升;摇臂的个数越多时，TBBA算法的性能提升速度越快，越具有优势。

4.3 TBBA_tree、TTBA算法实验结果

本节实验以棋类博弈问题中棋手挑选出当前盘面下最具优势的动作为例。将每个己方和对方的可行动作对视为一个摇臂，每个摇臂的评估结果（胜、负、平）视为一个三元分布，并构建了极大极小采样树模型。算法旨在识别根节点下的最

优动作。同样，叶子节点的分布概率值从臂空间中随机选择。

进行两组实验来验证本文提出的极大极小采样树最优动作识别算法（TTBA）的可行性和高效性。

第一组实验验证TTBA算法在树结构相同、上层下层确认难度组合不同的极大极小采样树中的性能。

本文设置了五

个3×3的两层极大极小采样树结构，它们的上下层确认难度

组合分别设定为：A表示上难下难，B表示上难下易，C表示

上易下难，D表示上易下易。最后，还构造了一个基于臂空间

分区

一的随机生成臂分布的E结构。在A、B结构中，TTBA算法、TBB_tree算法随着轮数的增加准确率逐渐上升，TTBA算法的准确率基本在TBBA_tree算法准确率区间的中值之上;并且，由于TBBA_tree算法在不同上下层轮数分配下得到不同的准确率，这造成实验结果有较大的标准差甚至还存在多个离群点。在C、D结构中，TTBA算法与TBBA_tree算法、U算法的性能都基本達到了100%准确率。在E结构中，由于树结构为3×3，每个节点下的动作集很小，因此上下层的三元多臂赌博机比较容易分辨。如图9所示，TTBA算法有最高的准确率且不会出现波动区间和异常值，其标准差为0。U算法和TTBA_tree算法在不同采样次数下的标准差如表4所示， 可以发现U算法相比TBBA_tree算法具有较大的标准差，即准确度波动更大。实验结果表明：在不同确认难度组合的树结构中，TTBA算法具有最优异的准确度性能，并且不会出现因上下层轮数划分而产生的异常值和波动区间。

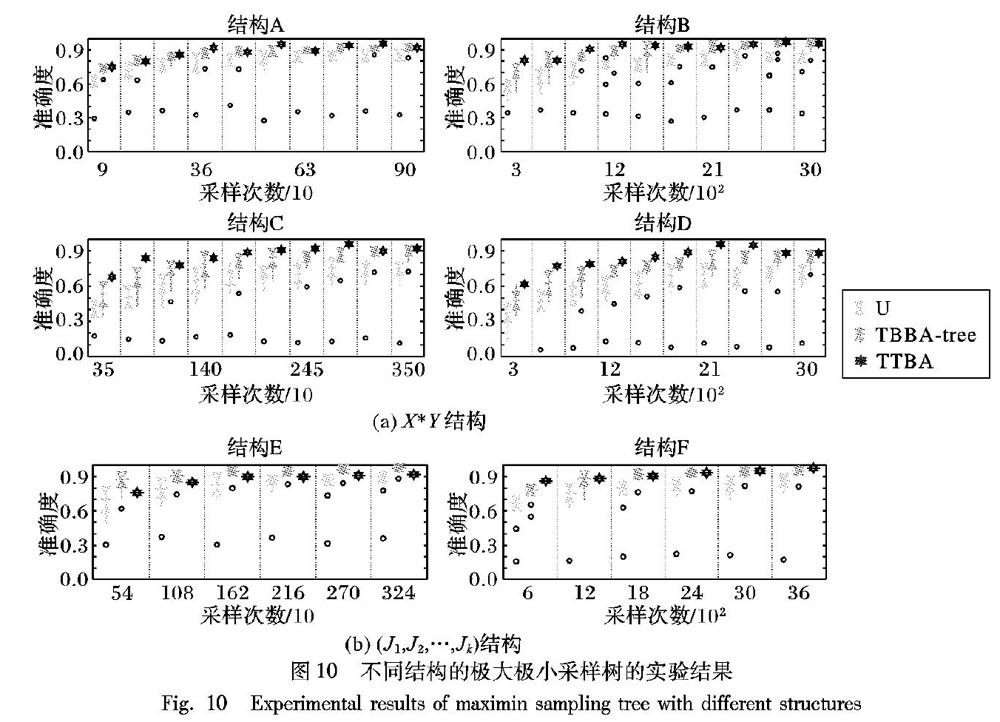
第二组实验验证TTBA算法在不同结构的极大极小采样树中的性能，树结构中臂分布基于臂空间一随机生成。本文首先设置了四种X×Y型树结构：A表示3×3、B表示10×3、C表示5×7、D表示3×10。X×Y表示根节点下有X个可行动作，每个第一层节点下有Y个可行动作。随着轮数的增加，TBBA_tree算法、TTBA算法在每个结构中整体保持着准确率上升的趋势，当轮数值较大时算法的准确率稍有下降。TTBA算法在A、B结构中的准确率基本能保持在TBBA_Ttree算法结果区间的上界浮动，与区间中值较为接近。在C、D结构中，TTBA算法的准确率基本能超越TBBA_Ttree算法结果区间的上界，并且其中多个实验结果表明TTBA算法的性能优势非常显著。TBBA_tree算法在C、D结构中实验结果的波动区间很大，对于算法性能丧失表示性，而TTBA算法依然保持优异的性能。

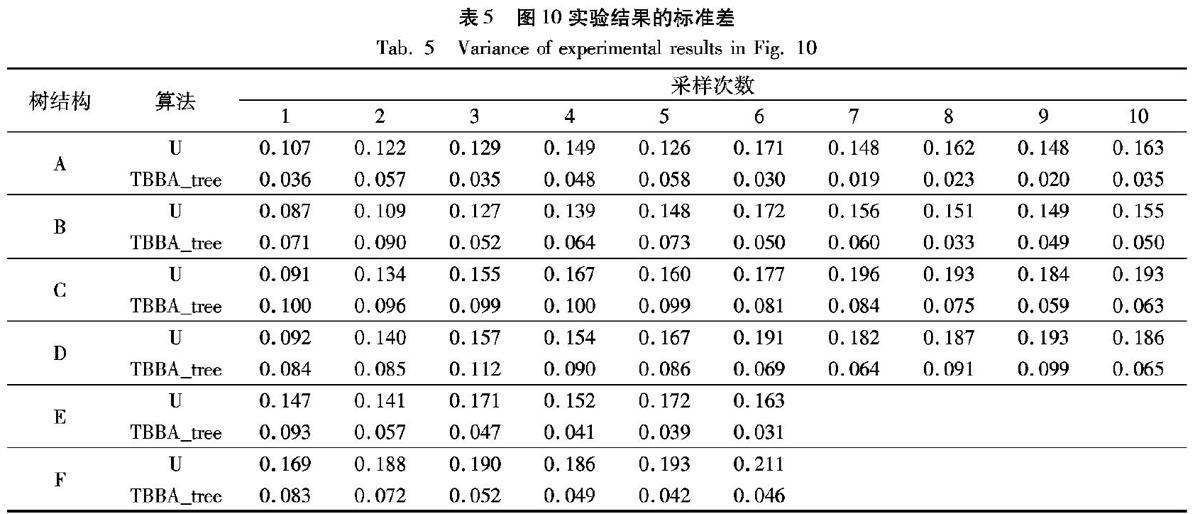
随后，还给出了两个特殊的树结构E：（18，3，9）和F：（2，4，6，6，12）（定义见3.1节的说明）。在E、F结构中，TTBA算法同样具有良好的性能，在不同的实验轮数下，准确率基本超过80%。如表5所示是U算法和TBBA_tree算法在不同采样次数下的标准差，可以看出U算法的标准差明显大于TBBA_tree算法，而TTBA算法在不同采样次数下的准确度都是一个数值，因此其标准差为0。

实验结果表明：TTBA算法在不同结构的极大极小采样树中都能保持稳定优异的性能，当树结构更加复杂时，TTBA算法的性能优势更加明显。

5 結语

本文构建了基于三元分布的多臂赌博机和极大极小采样树模型，并提出了一个基于贝叶斯思想和先验链的三元多臂赌博机最优臂确认算法TBBA;并进一步将TBBA算法应用到极大极小采样树结构中，给出了两轮零和博弈问题下的最优 动作识别算法TTBA。在实验部分，本文建立了两个精度不同的臂空间，并在其基础上构造了多个具有对比性的三元多臂赌博机、三元极大极小采样树结构，验证了本文所提出的TBBA、TTBA算法能够有效地识别集合中的最优对象。在未来的工作中，将基于本文的研究结果对不限深度、非满树的三元树结构进行研究，对其最优动作识别问题的算法和理论分析进行探索，使得算法更加适用于两名玩家完全信息零和博弈问题，并进一步探索强化学习问题[27-29]中的多名玩家非完全信息博弈问题。

参考文献

[1]  SILVER D， HUANG A， MADDISON C J， et al. Mastering the  game of go with deep neural networks and tree search [J]. Nature， 2016， 529（7587）： 484-489.

[2] SILVER D， SCHRITTWIESER J， SIMONYAN K， et al. Mastering the game of go without human knowledge [J]. Nature， 2017， 550（7676）： 354-359.

[3] SILVER D， HUBERT T， SCHRITTWIESER J， et al. A general reinforcement learning algorithm that masters chess， shogi， and go through self-play[J]. Science， 2018， 362（6419）： 1140-1144.

[4]  GARIVIER A， KAUFMANN E， KOOLEN W M. Maximin action  identification： a new bandit framework for games [C]// Proceedings of the 29th Annual Conference on Learning Theory. [S.l.]： PMLR， 2016， 49： 1028-1050. https：//arxiv.org/abs/1602.04676， 15 Feb 2016

[5] THOMPSON W R. On the likelihood that one unknown probability exceeds another in view of the evidence of two samples [J]. Biometrika， 1933， 25（3/4）： 285-294.

[6] BUBECK S， CESA-BIANCHI N. Regret analysis of stochastic and nonstochastic multi-armed bandit problems [J]. Foundations & Trends in Machine Learning， 2012， 5（1）：1-112.

[7] ROBBINS H. Some aspects of the sequential design of experiments [J]. Bulletin of the American Mathematical Society， 1952， 58（5）： 527-535

[8] KALYANAKRISHNAN S， STONE P. Efficient selection of multiple bandit arms： theory and practice [C]// Proceedings of the 27th International Conference on Machine Learning. Cambridge， MA： MIT Press， 2010： 511-518.

[9] EVEN-DAR E， MANNOR S， MANSOUR Y， et al. Action elimination and stopping conditions for the multi-armed bandit and reinforcement learning problems [J]. Journal of Machine Learning Research， 2006， 7： 1079-1105.

[10] KALYANAKRISHNAN S， TEWARI A， AUER P， et al. PAC subset selection in stochastic multi-armed bandits [C]// Proceedings of the 29th International Conference on Machine Learning. Cambridge， MA： MIT Press， 2012： 655-662.

[11] KAUFMANN E， CAPPé O， GARIVIER A， et al. On the complexity of best-arm identification in multi-armed bandit models [J]. Journal of Machine Learning Research， 2016， 17（1）： 1-42.

[12] MANNOR S， TSITSIKLIS J N. The sample complexity of exploration in the multi-armed bandit problem [J]. Journal of Machine Learning Research， 2004， 5： 623-648.

[13] GARIVIER A， KAUFMANN E. Optimal best arm identification with fixed confidence [C]// Proceedings of the 29th Annual Conference on Learning Theory. [S.l.]： PMLR， 2016， 49： 998-1027.[C/OL]// Proceedings of the 29th Annul Conference on Learning Theory， 2016 [2018-11-13]. https：//arxiv.org/pdf/1602.04589.pdf.

[14] AUDIBERT J-Y， BUBECK S， MUNOS R. Best arm identification in multi-armed bandits [C]// Proceedings of the 23rd Conference on Learning Theory. [S.l.]： PMLR， 2010： 41-53.

[15] BUBECK S， WANG T， VISWANATHAN N. Multiple identifications in multi-armed bandits [C]// Proceedings of the 30th International Conference on Machine Learning. [S.l.]： PMLR， 2013， 28（1）： 258-265.

[16]  SHAHRAMPOUR S， NOSHAD M， TAROKH V. On sequential  elimination algorithms for best-arm identification in multi-armed bandits [J]. IEEE Transactions on Signal Processing， 2017， 65（16）： 4281-4292.

[17] KAUFMANN E， KALYANAKRISHNAN S. Information complexity in bandit subset selection [C]// Proceedings of the 26th Conference on Learning Theory. [S.l.]： PMLR， 2013， 30： 228-251.

[18] CARPENTIER A， LOCATELLI A. Tight （lower） bounds for the fixed budget best arm identification bandit problem [C]// Proceedings of the 29th Annual Conference on Learning Theory. [S.l.]： PMLR， 2016， 49： 590-604.

[19]  GABILLON V， GHAVAMZADEH M， LAZARIC A. Best arm  identification： a unified approach to fixed budget and fixed confidence [C]// Proceedings of the 25th International Conference on Neural Information Processing Systems. Cambridge， MA： MIT Press， 2012： 3212-3220.

[20] CHAPELLE O， LI L. An empirical evaluation of Thompson sampling [C]// Proceedings of the 24th International Conference on Neural Information Processing Systems. New York： Curran Associates Inc， 2011： 2249-2257.

[21] MAY B C， KORDA N， LEE A， et al. Optimistic Bayesian sampling in contextual-bandit problems [J]. Journal of Machine Learning Research， 2012， 13（1）：2069-2106.

[22] KOMIYAMA J， HONDA J， NAKAGAWA H， et al. Optimal regret analysis of thompson sampling in stochastic multi-armed bandit problem with multiple plays[C]// Proceedings of the 32nd International Conference on Machine Learning. [S.l.]： PMLR， 2015： 1152-1161.

[23] BROWNE C B， POWLEY E， WHITEHOUSE D， et al. A survey of monte carlo tree search methods [J]. IEEE Transactions on Computational Intelligence & AI in Games， 2012， 4（1）：1-43.

[24] GELLY S， KOCSIS L， SCHOENAUER M， et al. The grand challenge of computer Go： monte carlo tree search and extensions [J]. Communications of the ACM， 2012， 55（3）：106-113.

[25]  TERAOKA K， HATANO K， TAKIMOTO E. Efficient sampling  method for Monte Carlo tree search problem[J]. IEICE Transactions on Information & Systems， 2014， E97-D（3）：392-398.

[26] KAUFMANN E， KOOLEN W M. Monte-Carlo tree search by best arm identification[J]. arXiv E-print， 2017： arXiv：1706.02986. Neural Information Processing Systems， 2017，30： 4897-4906.  https：//arxiv.org/pdf/1706.02986.pdf

[27] 高陽， 陈世福， 陆鑫. 强化学习研究综述[J]. 自动化学报， 2004， 30（1）：86-100. （GAO Y， CHEN S F， LU X. Research on reinforcement learning technology：a review [J]. Acta Automatica Sinica， 2004， 30（1）： 86-100.）

[28] 李宁， 高阳， 陆鑫，等.一种基于强化学习的学习Agent[J]. 计算机研究与发展， 2001， 38（9）：1051-1056. （LI N， GAO Y， LU X， et al. A learning agent based on reinforcement learning [J]. Journal of Computer Research and Development， 2001， 38（9）：1051-1056.）

[29] 蔡庆生， 张波. 一种基于Agent团队的强化学习模型与应用研究[J].计算机研究与发展， 2000， 37（9）：1087-1093. （CAI Q S， ZHANG B. An agent team based reinforcement learning model and its application [J]. Journal of Computer Research and Development， 2000， 37（9）： 1087-1093.）