如何确定外接球球心的位置

朱贤良

(安徽省枞阳县宏实中学 246700)

直观想象是数学核心素养的六大方面之一，强调借助几何直观和空间想象感知事物的形态与变化，利用空间形式特别是图形来理解和解决数学问题．在高中数学学习过程中，直观想象素养的培育与考查常通过三视图、空间平行与垂直、空间角与距离等问题的形式展开．随着全国高考命题的统一，有关空间几何体的外接球问题日益受到重视，成为考查直观想象素养的又一热门题型．

求解外接球问题的关键在于确定球心的位置，而确定球心位置的依据不外乎球心的两个特性：一是球心到球面上各点的距离都等于半径，二是球心与截面圆圆心的连线垂直于截面(球的截面圆性质)．由此出发，或利用一些特殊模型，或借助一般方法，即可让外接球球心毕露．

一、长方体的外接球

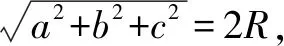
例1-1 (2017年高考全国Ⅱ卷·文15)长方体的长、宽、高分别为3、2、1，其顶点都在球O的球面上，则球O的表面积为____．

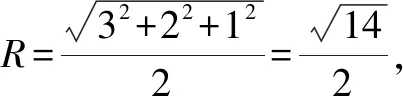
点评长方体是重要的立体几何模型，在认识空间结构特征、培养直观想象素养中发挥着基础的作用．在解决空间几何体的外接球问题时，要充分借助长方体模型的几何特征，简化求解过程．

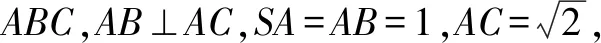
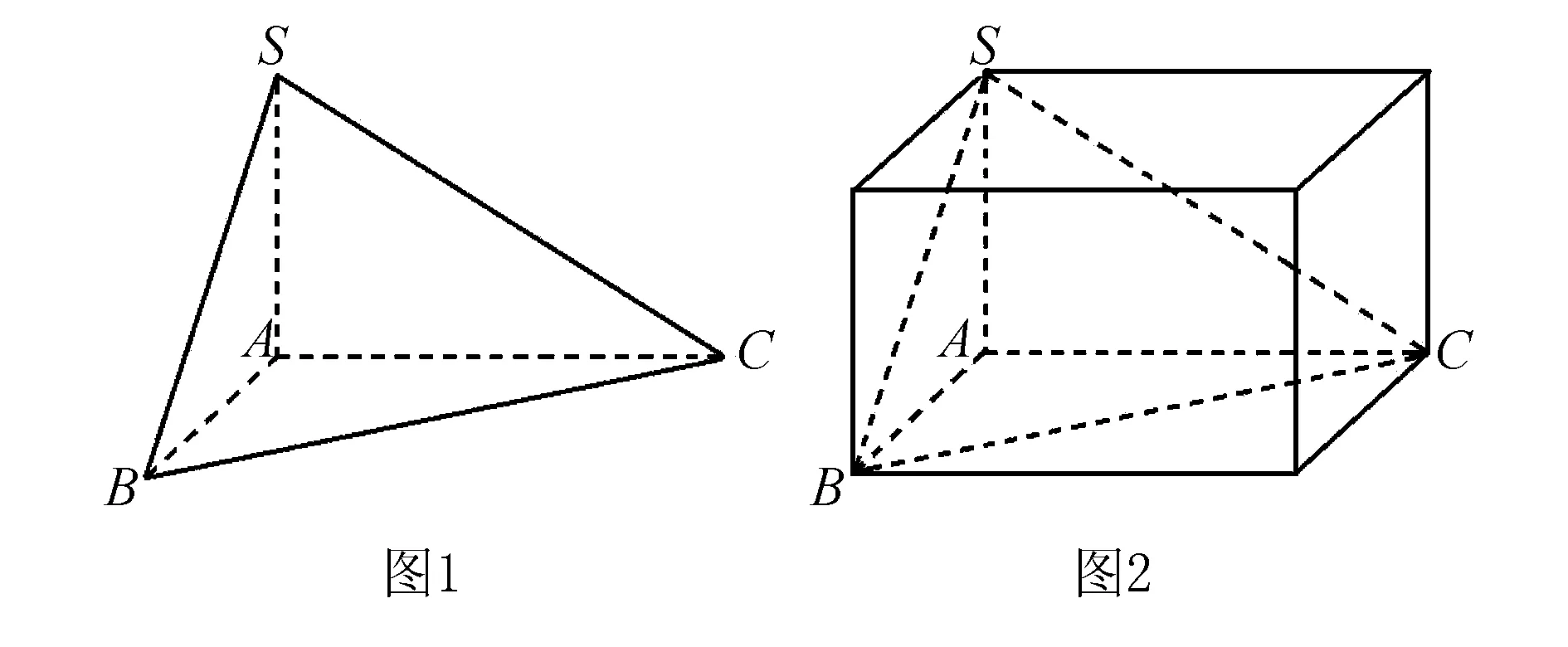
点评当三棱锥某一顶点处的三条棱两两垂直时，可将此三棱锥视为长方体的一角，进而借助长方体的外接球来实现求解．

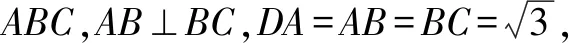
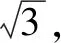
点评本题中，三棱锥D-ABC的底面△ABC为直角三角形，过锐角顶点A的侧棱与底面垂直，具备此几何特征的三棱锥(四个面均为直角三角形)即可补形成长方体．若过底面三角形的直角顶点B的侧棱垂直于底面，则此模型即为例1-2中的三棱锥．

简解因为四面体ABCD的三对对棱长对应相等，可将其分别视为长方体三对面的对角线，从而将四面体补形成长方体，如图5所示．

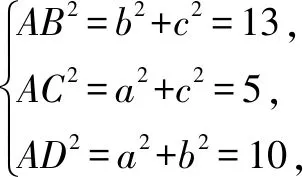
点评当三棱锥的三对对棱长对应相等时，此三棱锥也可以补形成长方体，三棱锥的三对对棱长即为长方体六个面的对角线之长．这种补形构造的思路较为隐蔽，解题时要注意判断与识别．又比如正四面体，可以通过这种思路将其补形成正方体．

例1-5(2013年高考辽宁卷·理10文10)已知直三棱柱ABC-A1B1C1的6个顶点都在球O的球面上．若AB=3，AC=4，AB⊥AC，AA1=12，则球O的半径为( ).

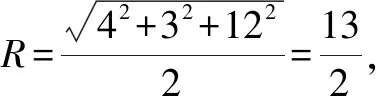
点评当直三棱柱的底面恰为直角三角形时，两个这样完全相同的三棱柱可拼接成一个长方体．需要注意的是，这里必须具备底面为直角三角形、侧棱与底面垂直这两个几何特征．

二、由共斜边的两个直角三角形所围成的三棱锥的外接球

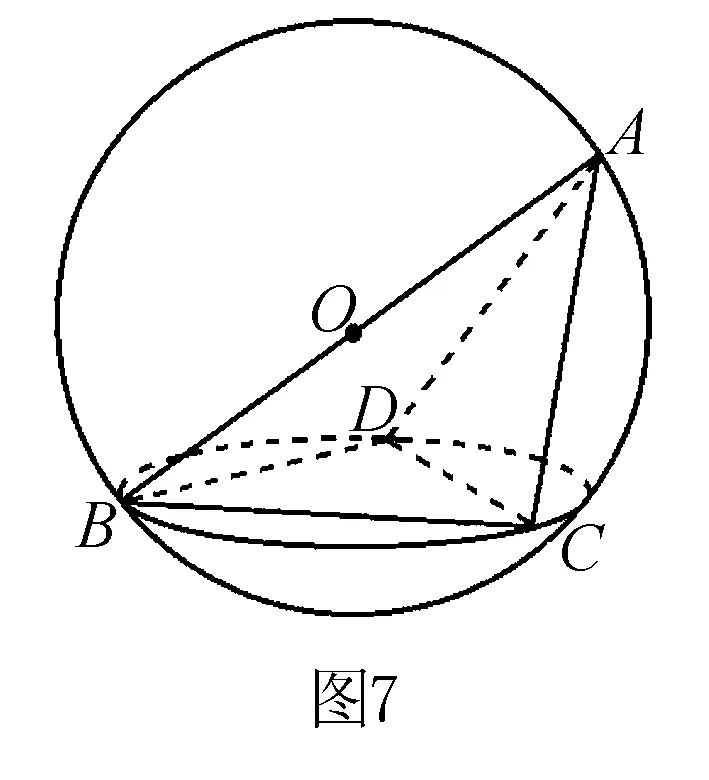
外接球的球心到球面上每一点的距离均为半径R，可以根据外接球球心的这一特征来确定球心的位置．比如，若四面体ABCD是由共斜边的两个直角三角形所围成的，如图7所示，△ABC与△ABD均为直角三角形，AB为公共的斜边，O为AB的中点，则根据直角三角形斜边中线等于斜边的一半可知，OC=OD=OA=OB，即点O到四点A,B,C,D的距离相等，故点O就是四面体ABCD外接球的球心，公共的斜边AB就是外接球的一条直径．

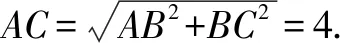
点评本题在求解过程中，需要从边长关系出发来认识三棱锥模型，把握“共斜边的两个直角三角形”这一典型几何特征．

A．2π B．4π C．6π D．8π

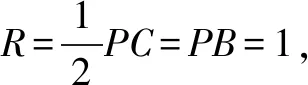
点评实际上，三棱锥P-BCO的四个侧面皆为直角三角形，也可以将其补形成长方体后再确定外接球球心的位置，解法同例1-3．

三、直棱柱的外接球

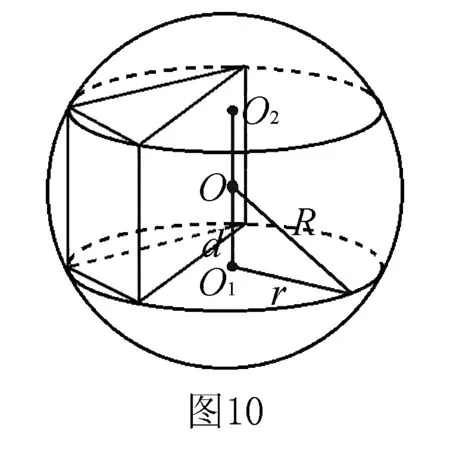
例3-1(2009年高考全国Ⅰ卷·理15)直三棱柱ABC-A1B1C1的各顶点都在同一球面上．若AB=AC=AA1=2，∠BAC=120°，则此球的表面积等于____．

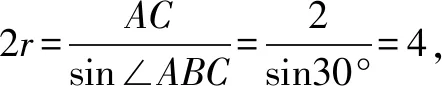
点评在计算底面外接圆的半径时，要注意结合几何图形及正弦定理求取．

点评根据平面几何特征，正六边形外心即中心与各顶点的连线将正六边形分割为六个全等的等边三角形，由此求得正六边形的面积及其外接圆的半径．

例3-3 已知某几何体的三视图如图11所示，则该几何体的外接球的表面积为( ).

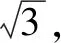
点评本题在求解时，要突破两个难点：一是根据三视图，准确还原几何体的结构特征；二是根据几何体的结构特征，灵活通过补形成直棱柱来确定外接球球心的位置及半径大小．

四、确定外接球球心位置的一般途径

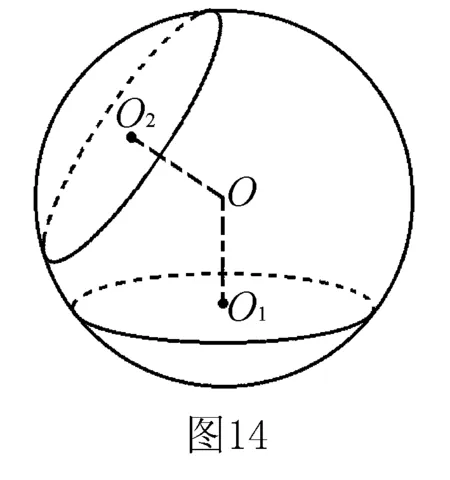
以上借助三类特殊多面体的结构特征来判定其外接球球心的位置，进而求解外接球的相关问题．除了要掌握上述特殊模型，还需要掌握确定外接球球心位置的一般方法．正是基于球心与截面圆圆心的连线垂直于截面，故多面体外接球球心必在过表面多面形的外心、且与表面垂直的直线上．如图14所示，过两截面圆的圆心且垂直于两截面的直线的交点即为球心O．

例4-1 如图15所示，在由边长为1的小正方形组成的网格中画出了某多面体的三视图，则该多面体的外接球的表面积为( ).

A．27π B．30π C．32π D．34π

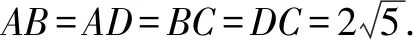
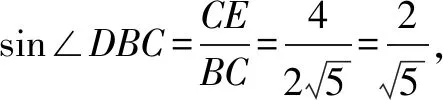
点评多面体外接球球心在过表面多面形的外心、且与表面垂直的直线上，而在选择表面多边形时要注意选择特殊形状的多边形，如正三角形、直角三角形、等腰三角形等，以比较容易地确定外心位置并求出外接圆半径大小．本题中，△BCD,△ABD为全等的等腰三角形，其所在平面又垂直，这有助于分析外心位置、确定线面的位置关系．

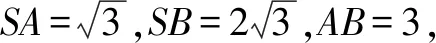
分别过O1,O2作平面SAB、平面ABC的垂线，则两垂线的交点O即为三棱锥S-ABC外接球的球心．

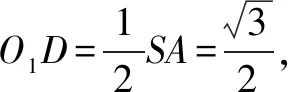
点评本题中，△SAB与△ABC分别为直角三角形、等边三角形，借助这两个特殊形状的三角形外心来确定外接球球心的位置，从而将问题转化为平面几何问题，体现了转化与化归思想，实现复杂问题简单化，从而使得问题迎刃而解．

通过立体几何的教学，发展学生的直观想象素养是数学教学的重要目标之一，它可以通俗地表示为“会想到、能解决”．比如本文在寻找几何体的外接球球心的过程中，注重结合一些常见、特殊、简单的几何模型来提取空间几何体的基本属性和几何特性，将问题求解程序化、规律化，降低问题解决的难度，达到“会想到、能解决”的效果．设计教学活动时，多引导学生对此类问题进行分类总结，进而把握几何关系的本质和规律，这无疑非常有助于学生空间想象能力的提升．