渗透系数空间变异性对堤基渗透稳定影响的数值模拟
2019-10-23
(长江科学院 水利部岩土力学与工程重点实验室,武汉 430010)
1 研究背景
土性参数具有较大的变异性,近年来在堤防风险管理中越来越受到关注。赵寿刚等[1]认为黄河大堤的复杂性和不确定性主要在于堤身和堤基土壤材料特性,将土壤渗透系数和密度视为随机变量,分析了不同淤背宽度的堤防渗流稳定性。土性参数的变异性可能也是堤基管涌险情发展具有一定程度不确定性的原因之一。
然而多数研究没有考虑土性参数的空间自相关性,仅将参数作为纯随机变量处理。实际上,土体在形成和改造过程中,受多种因素影响,具有显著的空间变异性,表现为土的性质既有随机性又有一定的空间相关性,这种空间变异性可用随机场[2]来描述。Griffiths等[3]研究了随机土体渗透系数对挡水建筑物下承压渗流场的影响,夏均民等[4]通过承压流算例分析了渗透系数的变异性对随机渗流场水头分布的影响。这些研究将渗透系数作为随机场进行渗流分析,考虑了渗透系数的空间相关性,但主要是针对承压流,而堤防渗流是有自由面的。
本文考虑渗透系数的空间变异性,将其作为随机场,采用蒙特卡罗方法分析堤防的渗流场分布及渗透稳定可靠性。
2 土体渗透系数的空间变异性
土层在形成过程中既呈现出一定的宏观结构规律性,又表现出局部随机性。在一定尺度范围内采取的土样中存在孔隙大小及团粒结构等方面的差异。土的颗粒或孔隙在空间上随机排列,同时存在不确定性的颗粒间作用力等[5],使土体介质及其土工参数存在非均匀性和随机性。
土工参数在空间上的分布具有一定程度的自相关性,直观地说,如果2个测量位置比较接近,那么得到的参数相近的可能性也较大;如果这2个位置相隔较远,那么测量参数之间可能没有相关性。从数学角度而言,可以通过空间相关函数或变异函数[6]来反映这种相关性。与相关函数紧密联系的是相关距离。在相关距离以内土工参数可认为是相关的,在相关距离以外土工参数则可认为是相互独立的。
Freeze[7]统计大量野外观测渗透系数空间变异性的结果,认为渗透系数可以用对数正态分布来描述,该结论被后来的研究者在随机水文地质研究中证实和广泛采用。Sudicky[8]在加拿大Borden含水层进行现场试验,经过分析得出渗透系数服从对数正态分布的结论。蔡树英等[9]在40×36 m2的壤土田块中对渗透系数进行了90个点的测量,经分析认为该田块中渗透系数为对数正态分布,方差为1.1,在此较小的测量范围内,渗透系数测量结果相差达到2个数量级。笔者等[10]对堤后200 m×100 m范围内表层砂性土渗透系数的空间变异性进行了分析,发现细砂渗透系数服从对数正态分布,空间相关结构可用指数模型描述。根据有关文献[11-12]报道的含水层或土壤的渗透系数空间变异研究成果,对平面取样尺度在1 000 m以内的相关尺度进行统计可以发现,水平方向最大为39 m,垂直方向最小为0.1 m,一般情况下水平方向的相关尺度大于垂直方向的相关尺度,反映了土体成层沉积的层状结构特征。
3 堤基渗流随机模拟方法
为了反映土体的空间变异性对渗流场的影响,可将渗透系数等参数作为随机场,如Vanmarcke[2]提出的土性剖面的随机场模型在岩土工程中得到较大应用。将参数随机场和反映物理规律的微分方程相结合并发展相应的数值方法,是进行随机分析的有力工具。当将渗透系数作为随机场时,渗流控制方程就成为随机偏微分方程,它的解不再是确定性的值,而是具有一定概率分布的随机函数。由于解析方法还不能求解复杂问题,因此从实用角度出发,本文采用蒙特卡罗(Monte-Carlo)方法进行计算分析。
首先,将渗透系数随机场离散为随机场单元,采用地质统计学中的转动带法[13]抽样模拟得到这些单元的渗透系数若干个样本模拟值,模拟值由下式确定,即
(1)
式中:ys为随机场模拟值;x为模拟域内的位置向量;yi为第i条线上的一维模拟值;ui为第i条线的方向向量;L为线的条数。然后,将他们作为确定性有限元方程各个单元的输入参数,求解渗流方程。采用有限元方法计算渗流场,稳定渗流场控制方程和定解条件通过有限元离散后可得到如下代数方程组,即
[K]{h}={B} 。
(2)
式中:[K]为渗透矩阵;{h}为未知水头列向量;{B}为边界列向量。
求解方程组(2)后可得到水头和渗透比降的抽样值,每一次渗透系数样本模拟值的输入都产生与其对应的水头和渗透比降的有限元解。最后,对所有计算结果进行统计,设总的抽样模拟数为N,则计算域内各结点水头和渗透比降的统计量即均值和方差可按以下统计公式计算,即
(3)
式中:μ为均值;σ2为方差;σ为标准差;x为统计对象,如水头。
当渗流产生的渗透比降J大于土体的临界比降Jc后就会引起土体的渗透变形破坏,据此可以建立渗透稳定可靠性分析的功能函数,即
在心功能改善方面,观察组LVESD、LVEDD及LVEF评分明显更高,差异有统计学意义(P<0.05),见表2。
Z=Jc-J。
(4)
当Z>0时,堤基土体处于渗透稳定状态;当Z=0时,处于极限状态;当Z<0时,则处于失稳或破坏状态。每次抽样模拟计算得到的功能函数值为Zi,若Zi<0的次数为m,则渗透失稳概率用下式估算,即
Pf=m/N。
(5)
式中Pf为渗透失稳概率。
4 算例分析
4.1 计算模型
下面结合具体算例进行计算分析。长江中下游某堤防断面如图1所示,由地勘资料可概化为4个渗透性分区:堤身及堤后平台为人工填土、堤基表层为砂壤土、堤基中部为粉质壤土、堤基下部为黏土。

图1 渗流计算断面示意图
根据试验结果统计,各土层渗透系数均值分别取为:人工填土9.0×10-6cm/s,砂壤土2.3×10-4cm/s,粉质壤土4.75×10-5cm/s,黏土5.25×10-6cm/s。堤基表层土临界比降为0.84。为简化分析,各计算参数的变异系数CV=σ/μ均取为30%。
根据已有研究,可以认为渗透系数服从对数正态分布。由于将渗透系数作为随机场,空间2个位置上的渗透系数值之间有一定程度的相关性,本文采用指数模型来描述这种相关性,即
ρ(τ)=e-2|τ|/θk。
(6)
式中:τ是两点之间的位置向量;θk是相关距离。
包承纲等[14]研究表明,对于一般的沉积土层,垂直相关距离约在0.2~2.0 m之间,而水平方向的相关距离可达到20~50 m。本文分析中,垂直方向和水平方向的相关距离分别取为1.5 m和30 m。
4.2 渗透系数随机场分布
对渗透系数随机场和渗流场进行了5 000次抽样模拟,图2为其中一次渗透系数抽样的空间分布。
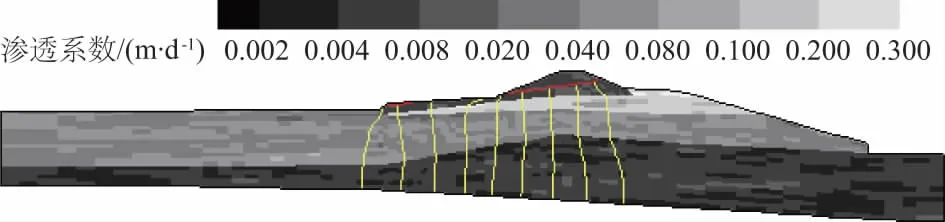
图2 渗透系数空间分布的一次抽样模拟
由图2可见,计算域内各单元上的渗透系数值均有所差异,体现了渗透性的空间变异,而传统的确定性渗流计算都将同一土层视为均质体,渗透系数作为常数,无法反映土体固有的空间变异性。图2中的渗透系数并不是杂乱无章的堆砌,而是满足一定的概率分布和空间相关性,在本文中采用了对数正态分布和指数结构模型,对于不同的问题也可根据具体试验资料进行统计。
对于渗透系数随机场的每一次抽样,即认为是对计算域内土体渗透系数空间分布的一次预测,以此作为模型输入所进行的渗流模拟,就是对该区域内渗流场可能出现结果的一次预估。图2中给出了相应的浸润线和等势线计算结果。由于每次的渗透系数分布都不一样,故每次的渗流模拟结果也有一定的差异。对于少量次数的抽样模拟,无法说明哪一次的计算结果更准确。那么对随机场进行大量抽样,然后对所有结果进行统计,得出渗流模拟结果的均值和方差等统计量,进一步可以计算渗流模拟结果出现的概率,并以此进行可靠性分析,以使计算分析在统计意义上更准确。
4.3 抽样次数对随机模拟收敛性的影响
为了检验模拟结果的收敛性,统计堤内脚下方人工填土的水头均值和方差,如图3所示,其中横坐标表示统计计算的抽样数,采用对数坐标。

图3 水头均值和方差统计结果随抽样次数的变化
由图3可见,水头均值和方差在模拟次数较少时具有较大的波动性,随着模拟次数的增加,水头的统计值逐渐趋于稳定,水头均值比方差收敛得要快。
堤内脚纵向轴线上的水头均值和方差分布如图4所示。水头均值除在接近堤脚位置有所减小其余位置几乎为常数,该轴线基本上是一条等势线。由于在渗流计算中堤脚作为出逸边界条件处理,水头是确定性的量,因此该处的水头方差为0,而在堤基下部土层中水头方差近似为常数。水头均值和水头方差的分布基本上呈对应关系,说明水头分布的变异性与渗流场分布有较大相关性。

图4 堤内脚纵向轴线上水头均值和方差分布
由于堤基土体临界比降的空间变异性统计资料尚不多见,考虑到随机场可以看作是空间上不同位置的随机变量的集合体,对于计算域内某一确定的位置,随机场退化为随机变量,因此本次将堤脚处的临界比降作为随机变量,也认为服从对数正态分布,由此可对堤脚处的临界比降进行抽样模拟,同时联合渗流场模拟得到的渗透比降,统计计算堤基渗透失稳概率。
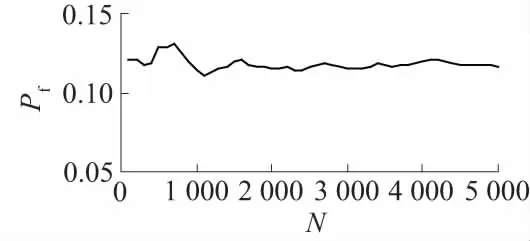
图5 堤基渗透失稳概率随抽样次数的变化
图5为不同抽样次数下的渗透失稳概率计算值,随模拟次数的增加,堤基渗透失稳概率趋向收敛于11.7%。
采用确定性渗流模型对上述算例进行计算,堤脚出逸比降达到0.42,小于其允许比降0.56,由此可能认为堤基没有渗透稳定问题。从可靠度理论出发,堤防发生渗透失稳的风险是存在的,但是具有一定的出现概率,因此,采用失稳概率作为安全评价依据具有一定科学性。需要指出的是,本文没有考虑洪水出现的概率,而将上游水位作为确定值,因此计算结果应该视为设计洪水位下堤防渗透失稳的条件概率。
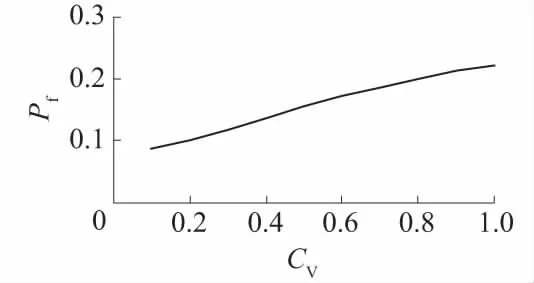
图6 渗透失稳概率随渗透系数变异系数的变化
4.4 随机参数对渗透失稳概率的影响
渗透失稳概率随渗透系数的变异系数的变化如图6所示,随着变异系数的增大,渗透失稳概率基本呈线性增长。渗透系数的变异性越大,土层的渗透性能越不均匀,土层中渗透比降的空间分布也越不均匀,可能造成局部渗流集中现象,从而导致渗透失稳概率增加。
图7给出了渗透失稳概率随临界比降变异系数变化的情况。由图7可见,渗透失稳概率随变异系数的增大而增大,但增加幅度随变异系数的增加逐渐变缓。临界比降的变异性越大,土层的抗渗性能越不均匀,在土层的薄弱环节可能造成局部渗流集中现象,从而导致渗透失稳概率增加。

图7 渗透失稳概率随临界比降变异系数的变化
5 结 论
(1)将渗透系数作为随机场,使得土性的空间变异性在工程渗流计算分析中能够较好体现。本文研究了考虑土体渗透系数空间变异性的堤防渗透稳定分析方法,可为堤防工程风险管理提供有效分析工具。
(2)结合堤防实例计算分析表明,随着渗透系数或临界比降的变异系数的增大,渗透失稳概率不断增大。这主要是由于土体空间变异性越大,其渗透性或抗渗强度的不均匀程度越大,容易造成局部渗流集中现象,从而引发堤基管涌等险情。
