一维土壤水分运动模型的有限体积法求解及其影响因素分析

李怡航

(四川大学水利水电学院，四川 成都 610065)

1 概述

降雨入渗是自然界中水循环的重要环节。降雨入渗是指降雨后水分从地表垂直向下进入土壤，促使土壤从不饱和状态向饱和状态转变的过程。水体渗流不仅可使粘土质岩石发生泥化、软化现象，还可促使膨胀土边坡或岩质边坡的体积膨胀，增大自重压力[1]，产生滑坡。可见对于渗流模型的建立是十分必要的。

在模拟入渗运动数值模拟方面，文献[2]中采用有限差分法对其进行求解，但此法对数值解的守恒性难以保证，在遇到边界条件和复杂区域时，会出现数值振荡和弥散现象。建立降雨入渗模型是分析边坡的稳定性较为常用的研究方法[3]，如陈守义用极限平衡分析法模拟的入渗模型[4]，于玉贞、刘金龙等利用有限元渗流分析的模型[5- 6]，而有限体积法结合了有限差分和有限元，其积分方程表示的是控制体积的通量平衡，因此数值解的守恒性得到了保障，相比于其他方法能有效地克服数值弥散和振荡现象[7]。

本文对一维Richards方程进行有限体积离散[8]，基于MATLAB语言编写一维入渗的程序，结合了木拉提等的中壤土入渗试验数据进行对比，从而来验证程序的可靠性。本文还分析了“降雨持时相同而降雨强度不同”和“降雨总量相同而降雨强度不同”两方面因素对一维入渗模型的空间分布规律进行分析。

2 数学模型及其求解

2.1 一维入渗运动的控制方程

本文研究的土壤水分垂直运动是针对单一土壤的，因此可假设其为均质、各向同性且骨架不变形的多孔介质。不考虑土壤中根系吸水的影响，Richards通过实验验证了非饱和土壤水运动符合Darcy定律[9- 10]，将其引入非饱和土壤水运动，结合Buckingham的能量法提出了不饱和土壤水运动的控制方程，土壤水分入渗运动用Richards方程描述为：

(1)

式中，θ—土壤体积含水率；K(θ)—土壤导水率；D(θ)—非饱和土壤水扩散率。

D(θ)根据其定义是导水率K(θ)和比水容量C(θ)的比值，即：

(2)

2.2 计算网格的处理

图1为一维垂直方向上入渗模型网格示意图。

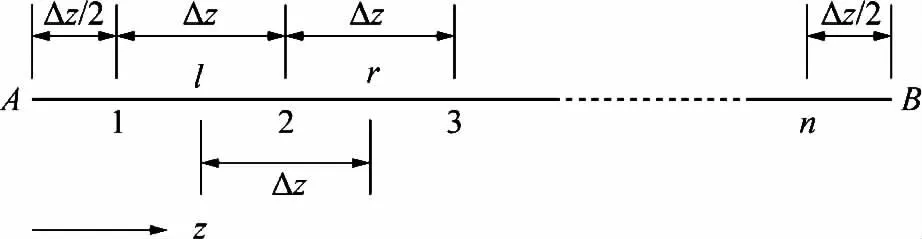
图1 入渗模型FVM示意图

在距地面垂直距离L这段空间中分为n个节点，空间步长选取Δz，并分别编号j=1～n，其中j=1和j=n的两处节点分别为计算模型的靠近上边界和下边界的节点，且距离边界距离Δz/2。时间步长选取Δt，时间层编序号依次为k=0，1，2，…。

本文选取控制体l-r为对象进行研究，由于点l、r并非模型中的节点，其K、D值不能直接获得，但可通过相邻节点L、M、R取近似值。

2.3 边界条件

2.3.1上边界条件的处理

(1)当上边界的土壤处于饱和状态时，为第一类边界条件。取控制体cv中包含节点j=1，且l即与上边界重合，因此：

2.3.2下边界条件的处理

入渗模型的下边界条件：θ(L，t)=θ0，即视作在x=L处的体积含水率不随时间的变化而发生变化，即该值为一恒定值。在节点j=n处截取控制体cv，则r与下边界重合，即：

2.4 模型求解

式(1)的有限体积法表述为：

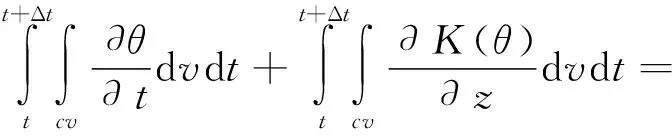
(3)

关于导水率，本文采用能适用于水流对流扩散的Up-wind格式，即：

(4)

关于扩散率，本文采用算术平均法，即：

(5)

因此，对于非边界节点(j=2，3，…，n-1)，式(5)最终求解可得下式：

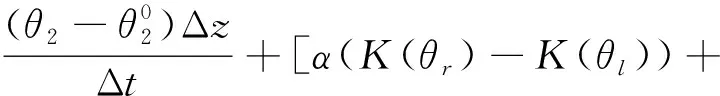
(6)

α的取值不同会产生不同的计算格式，其中最常用的有显式格式(α=0)、C-N格式(α=0.5)以及全隐格式(α=1)。其中全隐格式的各项系数均为正数，且对时间步长的选取是无条件稳定的，本文即选取全隐格式进行计算，即选取α=1，每一时间层的含水率分布均是通过多次迭代得到。

令r=Δt/Δz2，采用全隐格式后，式(6)可简化为：

aLθL+aMθM+aRθR=b

(7)

将上下边界条件进行有限体积离散，亦可得到式(7)，但其系数稍有不同。

由此，将各节点上含水量的计算表达式以矩阵形式表达：

(8)

其中对于每一节点j=2，3，…，L-1来说，aL=Aj、aM=Bj、aR=Cj。式(8)左边的第一个矩阵为为三对角矩阵，左边第二个矩阵与含水率有关，是未知矩阵，其中θ1、θL均是通过上下边界条件确定。求解上式可利用Matlab工具求解，计算流程如图2所示。

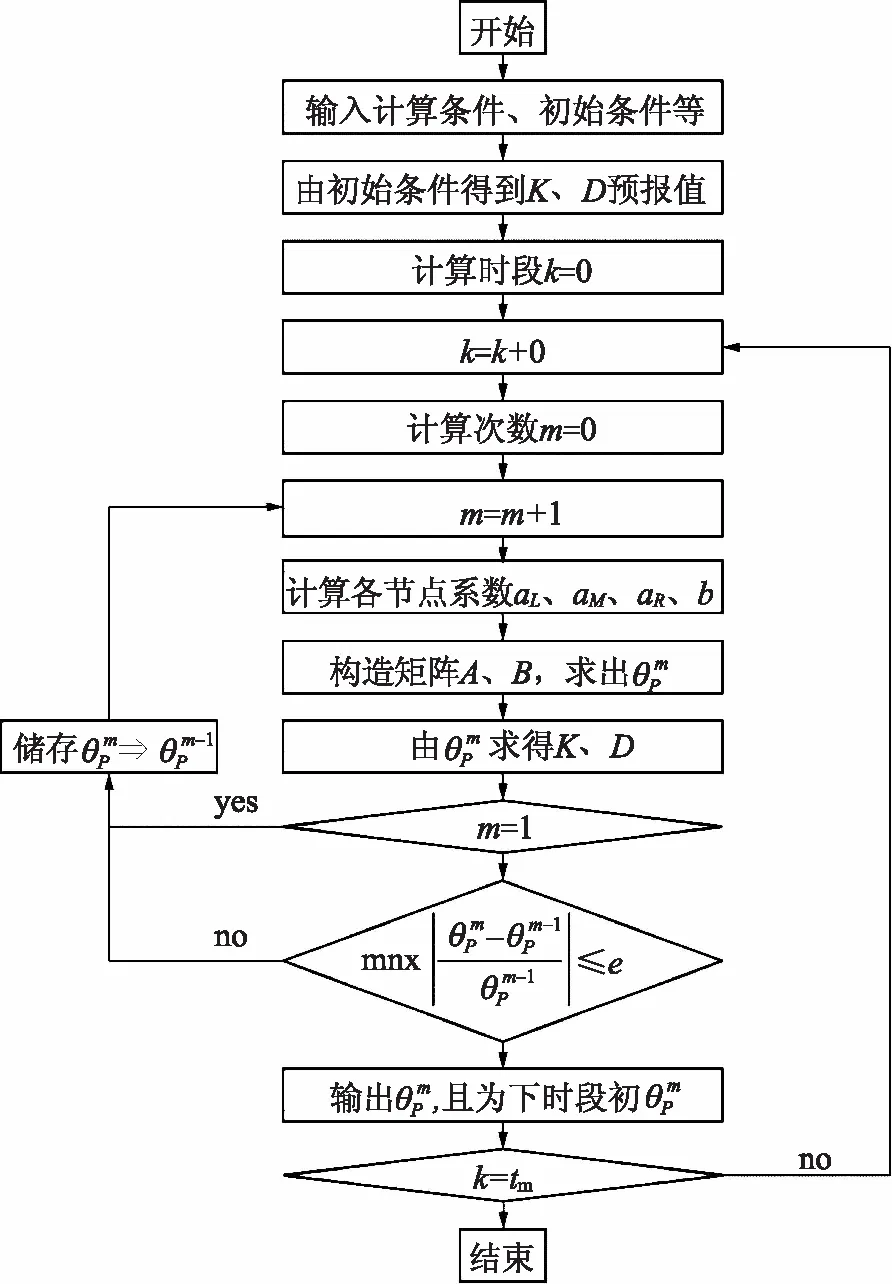
图2 入渗模型程序流程图

3 数学模型的验证

程序的有效性需要借助试验对模型求解的空间含水率分布进行验证。下面将通过木拉提·胡塞因等[11]对中壤土(其干容重为γd=1.4×103kg/m3)进行测试的室内试验数据进行程序验证。其试验的条件如下：

(1)初始条件：θ0=0.09(初始含水率)。

(2)边界条件：θs=0.42(上边界条件)θ|z=60=0.09(下边界条件)。

(3)参数选取：

计算时，空间步长选取Δz=1cm，时间步长Δt=1min。程序运算t=600，1230，1890min时各节点的体积含水量，最后程序运算结果与试验数据如图3所示，图3中计算结果同试验结果较为吻合。

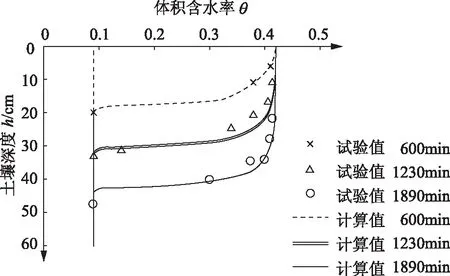
图3 入渗模型含水率空间分布图

在误差结果分析中，抽取试验数据在对应时刻对应深度的含水率计算值，与试验数据进行误差分析，得到表1。

由表1分析可知，采集的计算点其相对误差维持在15%以内，且绝对误差也控制在0.2以内，因此可以认为该程序运算结果是可靠的。

4 空间分布规律与因素影响分析

在验证章节2中的有限体积法模型的可靠性后，利用该模型对空间含水率分布进行进一步分析。在分析中采用文献[9]的试验，土壤类型为壤土，其参数有：塑性指数Ip=11.8，而干容重γd=1.365g/cm3。

初始条件：初始含水量沿垂直方向恒为0.028。

边界条件：上边界最高含水量达0.445。

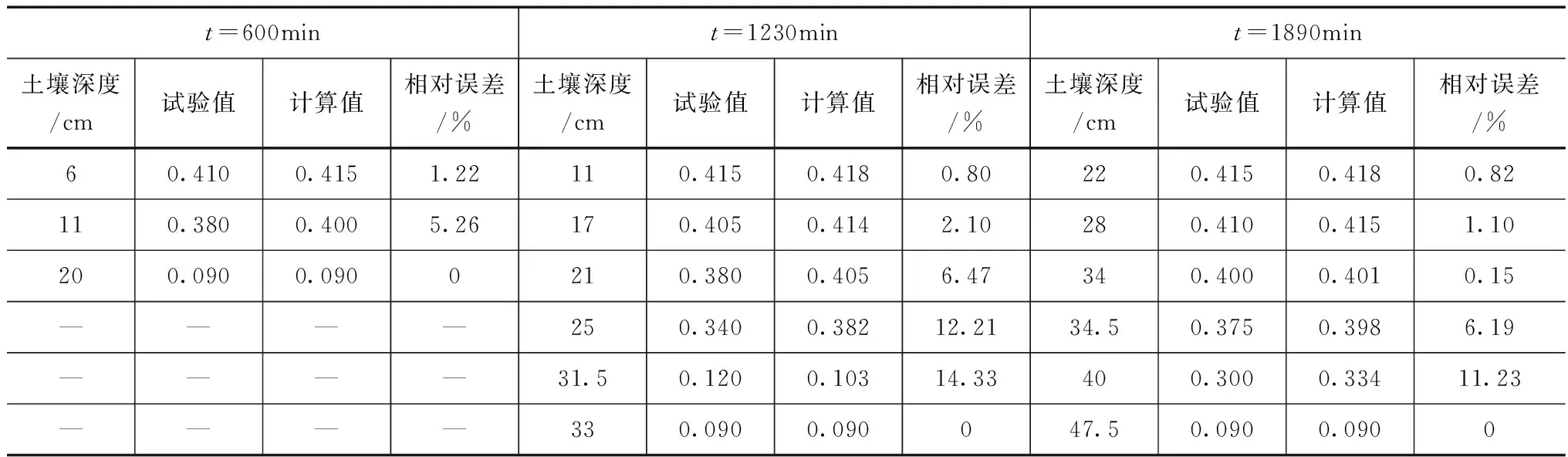
表1 误差分析表

D(θ)和K(θ)的关系式是经验公式，根据文献得到：

将编写的上述算例计算程序在Matlab R2017a软件上运行。将结果进行处理后对降雨入渗后的含水率空间分布曲线特征进行分析，取时间步长Δt=1min，空间步长Δz=1cm，降雨持时tm=1600min，降雨强度I=0.0500cm/min为例，其计算后得到的含水率空间分布曲线如图4所示。

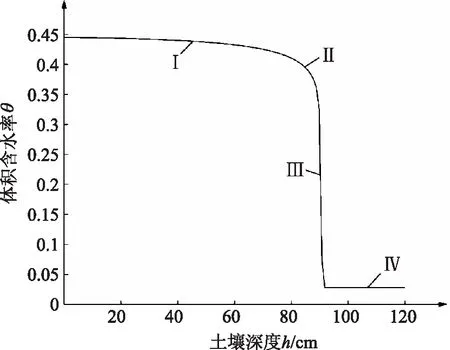
图4 含水率空间分布曲线及分段

该曲线与Green-Ampt[12- 15]入渗模型近似，湿润锋可近似看作水平线。该曲线可分成四段：

Ⅰ号曲线是从z=0cm出开始，该段曲线的含水率接近或达到饱和含水率，该段曲线近乎垂直。

Ⅱ号曲线的含水率随深度的变化已较为明显，但是该段曲线随深度增加，含水率值的减小幅度较小，且各点的切线角度已明显不是垂直或者水平。

Ⅲ号曲线的含水率变化非常明显，该段曲线几乎水平，且该段曲线即为入渗模型的湿润锋。

Ⅳ号曲线处于湿润锋前，其含水率随深度未发生变化，维持在初始含水率状态。

以“降雨持时相同而降雨强度不同”和“降雨总量相同而降雨强度不同”两方面因素对入渗模型的空间分布规律进行分析。

(1)降雨持时相同而降雨强度不同

从直观感觉上分析，降雨强度越大，入渗量越大，湿润锋深度zf越深。该观点是否正确，对程序输入时间步长Δt=1min，空间步长Δz=1cm，迭代次数为tm=1600min，降雨强度I分别为0.1000，0.0500，0.0250，0.0057cm/min，运算得到各降雨强度下最终含水率空间分布图如图5所示。

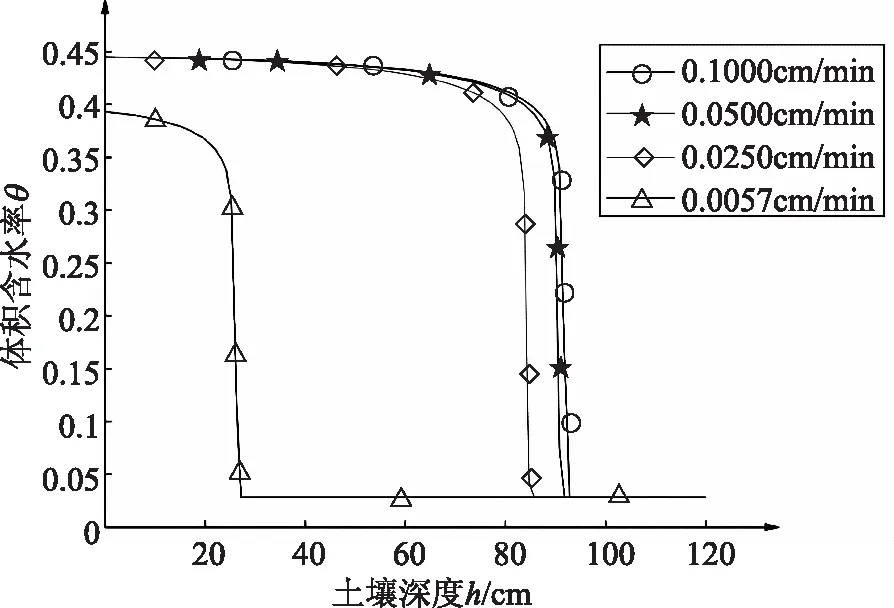
图5 不同降雨强度下含水率空间分布曲线

图5中四条线的分布符合“降雨强度越大，入渗量越大，湿润锋深度zf越深”的观点。但是，降雨强度0.1000cm/min、0.0500cm/min、0.0250cm/min之间的数量差距较大，但最终的入渗量与湿润锋深度差距却不是很大，这与降雨强度为0.0057cm/min的结果曲线却有极大差异。而且，0.0057cm/min强度的结果曲线含水率并未达到饱和状态。分析原因如下：

在降雨初期入渗能力是大于降雨强度的，因此在初期入渗强度等于降雨强度。随着持续的降雨，土壤含水率不断上升直至饱和，表层土壤的入渗能力却随着土壤含水率增加而减小。待其入渗能力等于降雨强度，坡面便开始产流(定义产流时刻的入渗能力为产流入渗能力，符号fp)，不过此刻表层土壤的含水率未必在饱和状态，入渗能力仍有可能继续下降。饱和后，土壤的入渗强度维持不变且小于降雨强度，因此表面能形成积水。

(2)降雨总量相同而降雨强度不同

取时间步长Δt=1min，空间步长Δz=1cm，以降雨总量为480mm设定了四个降雨事件，其降雨持时和降雨强度见表3。

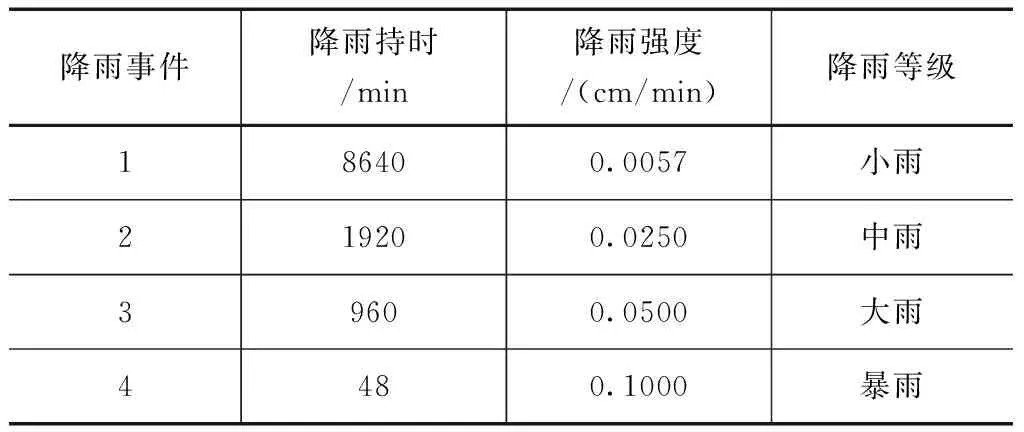
表3 降雨总量为480mm的不同降雨事件表

按照表3中事件所列述的降雨强度与降雨持时带入程序中，运算并绘制了降雨总量为480mm的不同降雨事件下含水率的空间分布曲线，如图6所示。

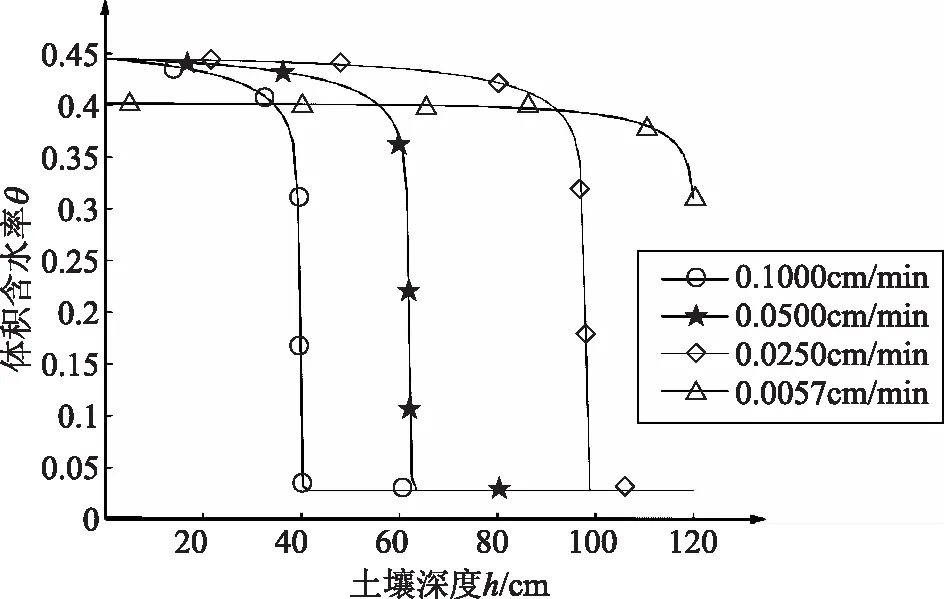
图6 不同降雨事件的含水率空间分布曲线

如图6所示，在降雨总量不变的情况下，随着降雨强度的减小，入渗量反而增加，湿润锋深度加深。当降雨强度为0.0057cm/min，降雨持时为8640min时，降雨入渗已达到计算深度，但是其表层无法形成积水，上层边界土也未达到饱和状态，降雨量全部入渗到土体中。

降雨强度越大，表层土壤含水率增加速率上升，产流时间缩短。因此，产流的时间以及产流量明显增加，造成这一现象的发生。这说明，降雨强度越低，形成的径流高度越小甚至无法形成径流。

5 总结

(1)本文推导了一维状态下降雨入渗模型控制方程的有限体积格式，结合上下边界的离散利用MATLAB程序对模型进行求解。并通过已知文献数据验证了入渗模型计算程序的可靠性，程序计算数据结果与文献试验记录结果接近，两者比较得到的误差均控制在15%以内，因此程序的计算结果是可靠的，可用于初步降雨入渗的预测与分析。

(2)从降雨强度和空间的关系对影响入渗模型的因素进行分析。当降雨持时相同而降雨强度不同，服从“降雨强度越大，入渗量越大，湿润锋深度zf越深”的规律，但若降雨强度小到一定程度则土壤各节点均不能达到饱和状态；当降雨总量相同而降雨强度不同，降雨强度越大，其产流时间越短，入渗量越少，湿润锋深度越浅。