新型组合模型在北方城市用水预测中的应用研究

雷付春

(辽宁省铁岭水文局，辽宁 铁岭 112000)

1 概述

城市用水预测对城市供水规划具有重要参考价值，对城市未来用水规划科学决策具有关键作用[1]。当前，城市用水预测逐步得到国内许多学者的关注，取得一定的研究成果[2- 6]，这些成果大都采用单一预测模型进行城市用水预测，而城市用水数据系列呈现较为明显的逐步增加且季节性变化不稳定特点，具有较强的非线性变化波动特点，因此传统单一预测模型不能充分反映城市用水原始数据特征，且存在预测质量不高，预测稳定性较差的特征[7]。综合考虑城市用水非线性变化波动且季节变化明显特点，结合季节性变化序列预测模型[8]以及粒子群算法[9]各自优点，构建一种新型优化组合预测模型，并以辽宁北部城市为研究实例，对日、月两种时间尺度的用水进行预测，并结合实测数据，在城市用水各时间尺度下，对比新型组合模型和传统单一模型预测的精度和稳定程度。研究成果对于北方城市用水规划以及水资源可持续利用具有重要的参考价值。

2 研究方法

采用季节变化序列预测模型对城市季节变化用水进行预测，结合粒子群算法对季节变化序列模型预测的非线性误差进行优化，从而实现预测误差的最小化。季节性变化序列预测模型将城市用水季节影响因子和非季节影响因子进行组合计算，计算方程为：

Ft=StCt-s+Yt=(St-1+Tt-1)Ct-s+Yt

(1)

式中，Ft—时间尺度t下的城市用水量，104m3；St—非季节的影响因子；Ct—季节影响因子；Tt—用水趋势变化因子；s—季节宽度因子；Yt—时段残差因子。

在预测模型构建基础上，需要结合实测城市用水数据进行拟合，模型数据拟合的方程为:

(2)

式中，B—计算因子；d—差分方程求解的阶数；D—季节性差分求解的阶数;S—模型差分求解的计算步长；at—差分求解的残差数据系列；Θ—模型的求解系数。

在季节性模型构建基础上，结合粒子群算法对其非线性误差进行优化，优化方程为：

Yi，d(t+1)=Yi，d(t)+aWi，d(t+1)

(3)

式中，t—寻优求解的次数；W—粒子算法的惯性权重指数；a—计算收敛速率因子。

在进行寻优求解时，结合全局优化求解算法对模型进行收敛计算，计算方程为：

v=vmax-t(vmax-vmin)/T

(4)

式中，v—寻优收敛速度控制因子；vmax、vmin—速度控制因子的最大值和最小值；T—模型寻优迭代求解的次数。

3 研究成果

3.1 研究区域概况

以辽宁北部某城市为研究实例，城市辖区内人口总数截止2018年为45.6万人，占总人口数的16.5%。区域多年平均水资源总量为32.56亿m3，多年平均用水水资源量为12.45亿m3，主要为农业、工业以及生活用水，其中农业用水比重较大，占45%左右，工业用水占30%左右，生活用水占比大约为15%。近些年来，随着城市人口的逐年递增，城市生活用水呈现较为明显的递增变化，年递增率为4.2%。为满足城市生活用水的需求，亟需对该城市生活用水进行科学规划，为此本文以该城市1990—2017年的城市用水统计数据作为模拟样本，与2018年城市生活用水数据对比分析，采用基于季节性变化序列预测模型以及粒子群算法组合模型对城市用水进行预测。预测结果对于该地区城市用水规划具有重要的参考价值。

3.2 模型参数估计及检验结果

对各模型参数进行估计，并结合两个准则对各模型参数估计结果进行检验，检验结果见表1。

从模型参数和检验结果可看出，模型的主要输入层为4层，模型参数估计训练目标为0.005，最大训练次数达到3000次。对模型各参数进行归一化的调整处理后，经过多次反复试验，当m值达到0.05时，其两个准则下模型预测精度达到最高。新型组合模型下其平均相对误差在-5.04，标准差为-0.015，通过了F检验。表明组合模型参数估计下已经无残差相关成分，模型可以用来进行变量预测。

3.3 组合模型在月尺度用水预测的对比结果

结合不同模型对研究区域月尺度用水预测结果进行对比，结果见表2，如图1所示。

从表2中可看出，相比于单一模型，新型组合模型下城市月尺度用水预测误差有较为明显的改善。单一PSO模型下误差最大，从图1中可看出，和原始数据相比，新型组合模型的贴切度最大，基本反映了月尺度城市用水的非线性变化特征，而传统的两种单一模型不能很好地反映月尺度城市用水的非线性变化特征；其次新型组合模型采用考虑季节性变化时间序列模型，能很好地反映城市用水的季节性变化特征；夏季属于用水高峰，因此这一时期用水预测值较大，而冬季用水量相对较低，新型组合模型也较好地预测了这一时期的用水量；新型组合模型由于结合PSO算法对其误差收敛进行优化，使得模型的误差降低。从相关性分析结果可看出，相比其他两种单一预测模型，新型组合模型的计算散点更为集中，相关程度较高，表明新型组合模型其预测质量更为稳定。

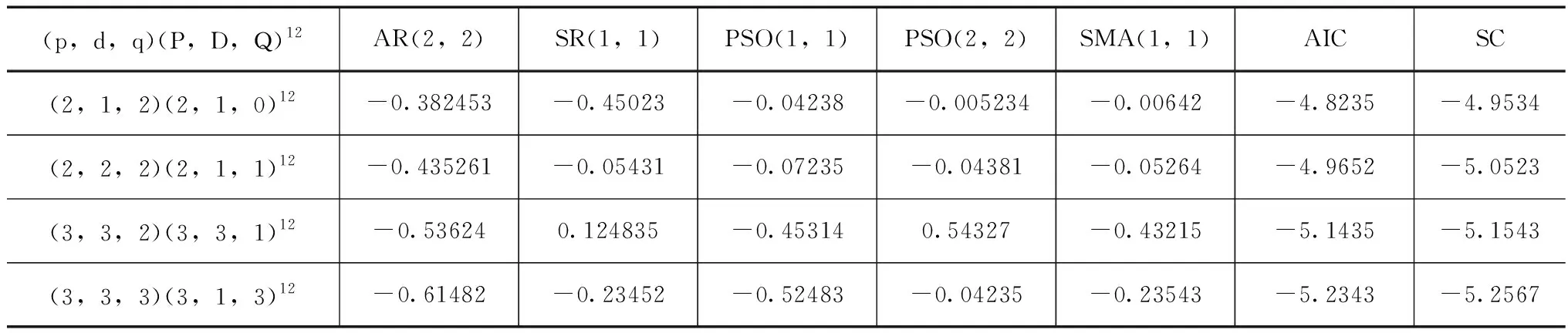
表1 各模型参数检验及估计结果

表2 不同模型城市用水预测对比结果

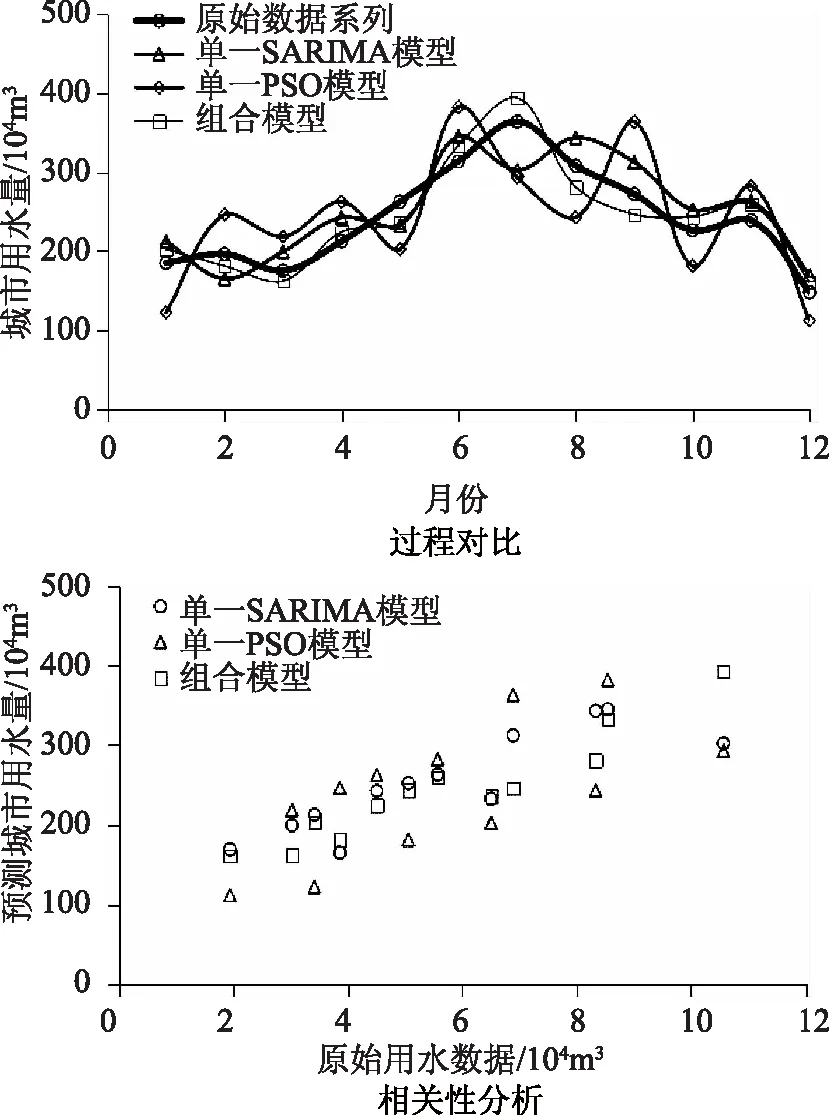
图1 不同模型月尺度城市用水预测情况对比

3.4 组合模型在日尺度用水预测的对比结果

城市日用水统计数据系列样本较少，为此结合内插数据系列和实测数据系列两种方式，分别对不同模型下城市日用水预测结果进行对比，结果见表3—4，如图2所示。

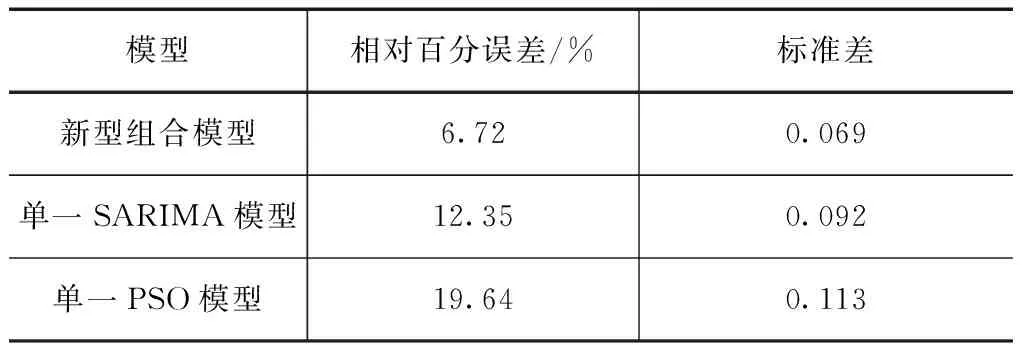
表3 不同模型在日尺度用水预测数据对比(内插数据系列)

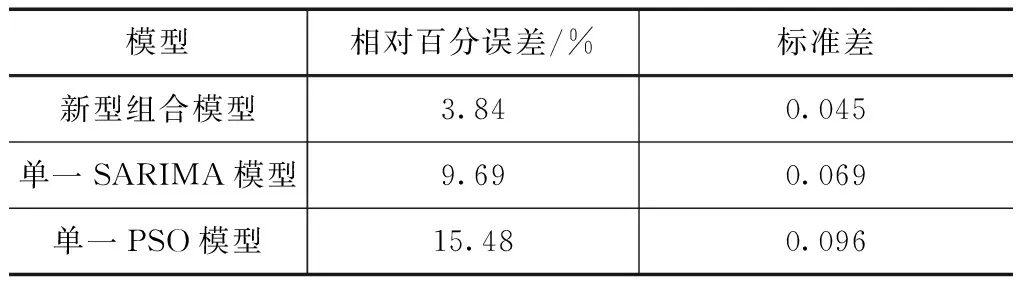
表4 不同模型在日尺度用水预测数据对比(实测数据系列)

图2 不同样本数据系列下各模型预测对比结果

从表3—4中可看出，相比于单一模型，新型组合模型在标准差和相对百分误差上均有不同程度的改善，标准差表征的是模型计算的稳定性，从标准差分析结果可看出，相比于单一模型，新型组合模型在标准差平均提高0.035，计算质量更高;这主要是结合粒子群算法对季节变化序列模型预测的非线性误差进行优化，从而实现预测误差的最小化。从内插数据系列和实测数据系列对比结果可看出，各模型在两种类型数据预测的标准差和相对百分误差差别不大，因此对于预测数据系列来说，内插数据系列也可以作为城市日用水预测的样本数据系列。从图2中可看出，采用实测数据系列后，日用水变化波动性低于采用内插数据下的，而这种日用水变化波动性也使得各模型下预测值和原始值之间的散乱度有所增加，在内插数据系列下，各模型预测值的变动度较大，新型组合模型下预测的日用水吻合度好于其他模型，基本能反映日用水变化的波动性，但存在一定的系统偏小的变化趋势。而从实测数据系列对比结果可看出，相比于内插数据系列，实测数据系列下的波动变化特征有所减弱，新型组合模型和实测数据系列的吻合度要好于内插数据系列，且系统偏小的变化趋势有所减弱，这主要是因为内插数据系列增加了样本数据系列的误差性，使得误差呈现叠加效应，增大了各模型下预测的误差值。

4 结论

(1)季节变化序列模型符合水资源量的非线性波动特征，采用粒子群算法对该序列模型预测的非线性误差进行优化，将两个模型进行组合的预测方法可有效降低模型误差，组合模型在水资源其他领域预测具有推广价值。

(2)组合模型在各时间尺度上预测误差较传统单一模型均明显改善，且计算稳定性好于单一模型，该组合模型不仅拓宽了模型的适用范围，也解决了模型在不同时间尺度下预测结果有所冲突的局限。