立足二次方程概念 梳理判别式要点
2019-10-22文熊冬平
文熊冬平
一、要点梳理
要点一:一元二次方程根的判别式。
一元二次方程 ax2+bx+c=0(a≠0)中,b2-4ac叫做一元二次方程ax2+bx+c=0(a≠0)的根的判别式:
(1)当b2-4ac>0时,一元二次方程有两个不相等的实数根;
(2)当b2-4ac=0时,一元二次方程有两个相等的实数根;
(3)当b2-4ac<0时,一元二次方程没有实数根。
要点诠释:
利用根的判别式判定一元二次方程根的情况的步骤:①把一元二次方程化为一般形式;②确定a,b,c的值;③计算b2-4ac的值;④根据b2-4ac的符号判定方程根的情况。
要点二:一元二次方程根的判别式的逆用。
在一元二次方程ax2+bx+c=0(a≠0)中:
(1)方程有两个不相等的实数根⇒b2-4ac>0;
(2)方程有两个相等的实数根⇒b2-4ac=0;
(3)方程没有实数根⇒b2-4ac<0。
要点诠释:
(1)逆用一元二次方程根的判别式求未知数的值或取值范围,不能忽略二次项系数不为0这一条件;
(2)若一元二次方程有两个实数根,则b2-4ac≥0。
二、典型例题
一元二次方程根的判别式的应用。
例1 已知关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不相等的实数根,求k的取值范围。
【思路点拨】已知方程有两个不相等的实数根,即b2-4ac>0,得到关于k的不等式,从而求得k的范围。
【解析】a=1,b=2k+1,c=k2+1。
b2-4ac=(2k+1)2-4(k2+1)=4k-3。
∵关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不相等的实数根,
∴4k-3>0。
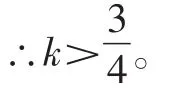
【总结升华】我们应熟练掌握一元二次方程根的判别式与根之间的对应关系,同时要注意书写格式。
拓展已知关于x的一元二次方程x2+(m+2)x-m2+m+1=0。
(1)求证:不论m为何值,该方程总有实数根;
(2)当方程有两个相等的实数根时,求m的值及方程的根。
【解析】(1)证明:∵a=1,b=m+2,c=-m2+m+1,
∴b2-4ac=(m+2)2-4(-m2+m+1)=5m2≥0。
∴不论m为何值,该方程总有实数根。
(2)解:∵方程两个实数根相等,
∴b2-4ac=0。
即5m2=0,m=0。
当m=0时,原方程为x2+2x+1=0。
解得:x1=x2=-1。
例2 已知关于x的方程mx2-(m+2)x+2=0。
求证:不论m为何值,该方程总有实数根。
【思路点拨】我们应注意本题并没有说方程是一元二次方程,也没有说方程有两个实数根,因此二次项系数可以为0,也可以不为0。
【解析】①当m=0时,原方程为一次方程,此时x=1,
∴当m=0时,方程有实数根;
②当m≠0时,b2-4ac=[-(m+2)]2-4×m×2=(m-2)2,
∵(m-2)2≥0,
∴方程有实数根。
综上所述,无论m为何值,该方程总有实数根。
【总结升华】(1)应用判别式的条件是方程为一元二次方程,当二次项系数为字母时,应注意系数不为0;
(2)应用判别式应将方程化为一般形式;
(3)注意有实根和有两个实根的区别。
拓展已知关于x的方程kx2-(k+2)x+2=0。若k为任意实数,判断方程根的情况并说明理由。
【解析】①当k=0时,-2x+2=0,x=1。
②当k≠0时,b2-4ac=[-(k+2)]2-8k=(k-2)2。
∴当k=0时,方程有一个实数根;
当k=2时,(k-2)2=0,方程有两个相等的实数根;
当k≠2且k≠0时,(k-2)2>0,方程有两个不相等的实数根。
