高超声速飞行器发射坐标系导航算法
2019-10-22沈付强孙晗彦
陈 凯,沈付强,孙晗彦,周 钧
(西北工业大学航天学院,西安 710072)
0 引 言
临近空间是距地面20~100 km的空域,临近空间高超声速飞行器具有在临近空间以超过5倍声速长时间巡航飞行的能力[1]。2004年3月27日,X- 43A高超声速飞行器试验成功,标志着人类开发临近空间进入了一个快速发展的阶段[2]。
临近空间介于传统的航空和航天飞行器空域之间,针对不同的临近空间飞行器,世界各国学者尝试了多种导航参考坐标系来设计临近空间导航算法,取得了很好的结果。Stephen为SHEFEX2高超声速飞行器研究了地心惯性坐标系下的捷联惯导算法[3]。Yang等[4]采用地心地固坐标系[5]研究了高超声速飞行器GFSINS/GPS/CNS组合导航算法。Yu等[6]采用东北天当地水平坐标系作为高超声速飞行器导航参考系;X- 43A高超声速飞行器采用的Honeywell公司的H-764系列INS/GPS组合导航系统,X- 43A的飞控计算机与SLAM-ER防区外导弹相同,采用了当地水平坐标系导航算法[7],这是多数高超声速飞行器采用的导航坐标系。另外,熊智研究了发射惯性坐标系下的空天飞行器SINS/GPS/CNS多信息融合组合导航算法[8-9]。作者在给出发射惯性坐标系下捷联惯导算法的同时,还介绍了如何将发射惯性坐标系的导航数据转换到当地水平坐标系下[10],并且证明了发射惯性坐标系和当地水平坐标系导航信息的等价性[11]。
导航参考坐标系的选择,不仅仅是飞行器导航专业的问题,还涉及飞行弹道、制导和控制等方面[2]。以助推-滑翔高超声速飞行器为例,其飞行剖面主要包括助推段、自由弹道段、弹道再入段、弹道爬升段和滑翔段等飞行阶段。从飞行阶段来看,助推段、自由弹道段、弹道再入段和弹道爬升段等阶段,属于航天领域的飞行弹道,控制系统需要航天体系下(如发射惯性坐标系)的导航数据来进行飞行控制;而滑翔段飞行器沿着地球表面飞行,以地球表面作为参考,属于航空领域的飞行弹道,控制系统期望航空体系下(如当地水平坐标系)导航数据来进行飞行控制。可见,高超声速飞行器具有航天和航空的双重飞行控制和导航需求。
发射惯性系用来描述弹道导弹、运载火箭等航天器的姿态和位置,适用于垂直发射,有利于飞行器入轨后的轨道计算,不适合描述飞行器与地面的相对关系;而当地水平坐标系用来描述运载器在近地运动中的姿态和位置,不适合垂直发射。二者都不能同时满足助推-滑翔飞行器的导航需求,本文选择发射坐标系作为导航参考坐标系,对上述问题提出解决思路。
1 发射坐标系惯性导航算法
1.1 坐标系
文中使用到以下坐标系[12],选择发射坐标系作为导航参考坐标系。
1) 地心惯性坐标系(地惯系,i系),原点为地球中心,xi,yi轴在地球赤道平面内,xi轴指向春分点,zi轴为地球自转轴。
2) 地心地固坐标系(地固系,e系),原点为地球中心,xe,ye轴在地球赤道平面内,xe指向本初子午线,ze轴为地球自转轴。
3) 载体坐标系(载体系,b系),坐标原点为飞行器的质心,x轴指向头部,y轴在飞行器的主对称面内,向上为正,载体系为前上右坐标系。
4) 发射坐标系(发射系,g系),坐标原点与发射点固连,xg轴在发射点水平面内,指向发射瞄准方向,yg轴垂直于发射点水平面指向上方,发射系为前上右坐标系。
5) 发射惯性坐标系(发惯系,a系),飞行器起飞瞬间,坐标原点与发射原点重合,各坐标轴与发射系各轴也相应重合。飞行器起飞后,发惯系各轴方向在惯性空间保持不动。
1.2 发射系下的算法编排
式(1)为发射系下导航方程[9],图1为发射系捷联惯导机械编排图。
(1)
(2)
式中:φ,ψ,γ分别为发射系俯仰角、偏航角和滚转角。
1.3 导航数值更新算法
1.3.1姿态更新
姿态更新的数字递推形式为
(3)
(4)
式(4)进一步计算为:
(5)
式中:T=tm-tm-1。
(6)
采用二子样算法,则有:
(7)
(8)
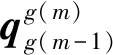
1.3.2速度更新
由发射系下导航方程(1)可得速度更新的数字递推算法
(9)
(10)
(11)
(12)
其中,各参数在tm-1和tm-2时刻均是已知的。
(13)
(14)
记
(15)
又因
(16)
故式(14)可变为
(17)
其中
(18)
到此完成速度更新。
1.3.3位置更新
与捷联惯导姿态和速度更新算法相比,位置更新算法引起的误差较小,可采用梯形积分方法对位置方程离散化,得
(19)
式(19)移项,便可得到位置更新算法
(20)
以上介绍了姿态、速度和位置更新算法,关于发射系到当地水平系导航信息的转换,文献[12]有相关介绍。
2 发射系下的SINS/BDS组合导航
2.1 BDS卫星数据的转换
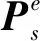
(21)
(22)
(23)
(24)
2.2 SINS/BDS组合导航算法
2.2.1姿态误差方程
发射系下的姿态误差方程为
(25)
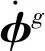
2.2.2速度误差方程
发射系下的速度误差方程为
(26)

且gg为发射系引力矢量的计算公式
(27)

将式(27)写成分量形式为
(28)
则

(29)
2.2.3位置误差方程
发射系下的位置误差方程为
(30)
2.2.4SINS/BDS组合导航方程
(31)
卡尔曼滤波状态方程为
(32)
其中,G为噪声驱动矩阵,W为过程噪声矢量,且状态转移矩阵F为
(33)
SINS/BDS组合导航的量测方程为:
Zvp=HvpX+Vvp
(34)
其中,Zvp为速度位置量测矢量,
(35)
Vvp为速度位置量测噪声,观测矩阵Hvp的表达式为
(36)
3 SINS/BDS组合导航仿真
设计一条时长1100 s的高超声速飞行器飞行轨迹[13-14],该轨迹的初始状态为:速度为0 m/s,纬度为34.2°,经度108.9°,高度为0 m,射向为200°,俯仰角为90°,横滚角为0°,偏航角为0°。飞行轨迹如图2所示。
对提出的组合导航算法进行仿真分析,表1给出了仿真参数表,图3~图7为SINS/BDS组合导航的仿真结果。
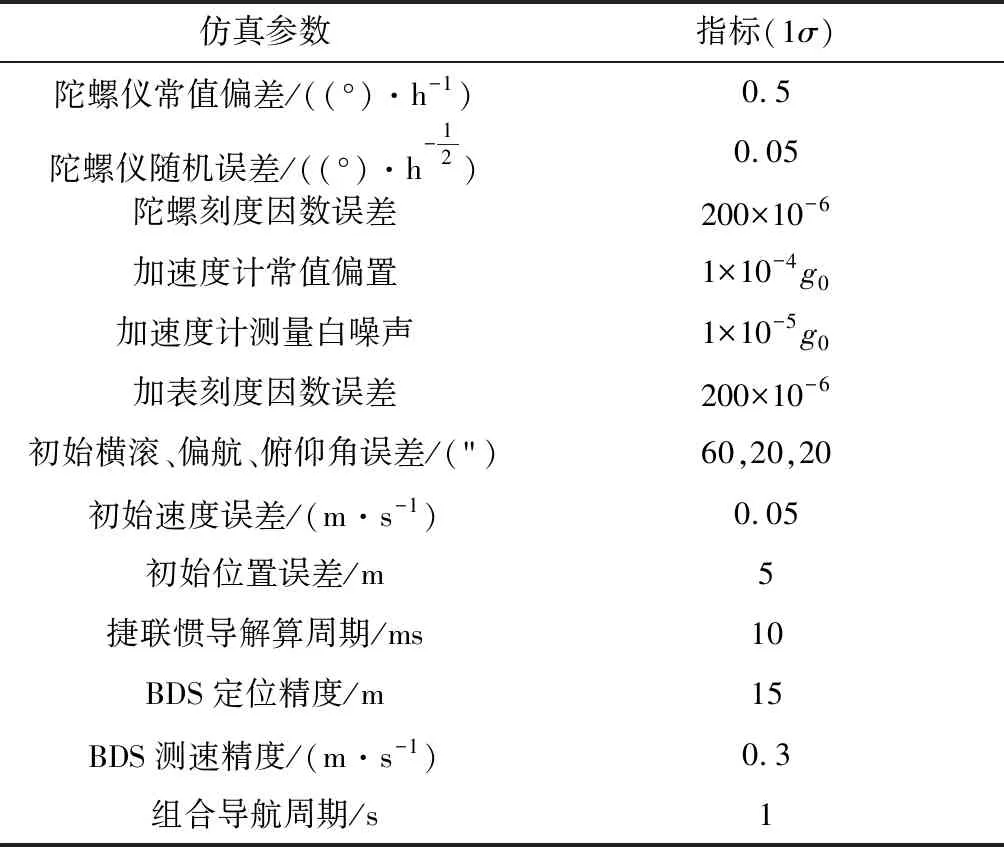
表1 SINS/BDS组合导航仿真参数表Table 1 Parameters of SINS/BDS simulation
从图3~图7可以看出,组合导航系统的三个姿态角误差基本能收敛到0.05°以内;三个方向的速度误差能收敛到0.2 m/s以内;三个方向的位置误差能收敛到10 m以内;500 s后,三个方向的陀螺漂移都能估计为0.5°/h;400 s后,x和y方向的加速度计漂移都能估计为0.1 mg,由于z向运动很小,该方向加速度计漂移估计效果不好。
发射系与地球固联,其位置、速度和姿态导航参数是相对于地球的,与很多地面发射飞行器飞控系统需求的导航信息一致;与发惯系导航参数相比,有利于人的直观描述和理解。在垂直发射情况下,发射系的姿态角不会奇异,而这种情况下当地水平坐标系的姿态角会发生奇异现象。发射系采用J2重力模型,考虑了当地水平的南北向重力影响,适用于临近空间飞行高度的标准重力计算。发射系导航特别适合于在发射面内飞行的中近程地地飞行器。
4 结 论
设计了发射系下捷联惯导算法和组合导航算法,并进行了仿真校验。研究的发射系导航算法可以为其它临近空间飞行器的导航算法设计提供参考。
