于Matlab的双机器人协作空间求解及分析

2019-10-21王威许勇刘勇宋伟基

郑州轻工业学院学报(社会科学版) 2019年4期

王威许勇刘勇宋伟基

摘要：以双机器人协作系统模型为研究对象，根据其D|H参数求出运动学正解，基于Matlab，利用蒙特卡洛方法解出双机器人工作空间的公共区域，采用极值理论法和搜索区域法对公共区域边界曲线进行提取，可确定双机器人协作空间的界限曲面和极限位置.仿真结果表明，该方法具有易于实现、空间表达直观等优点，可应用于其他结构形式和任意自由度的双臂机器人类似问题求解.

Abstract：Taking the double|robot cooperation system as the research object， the kinematics positive solution was obtained according to its D|H parameter. Based on Matlab， the Monte Carlo method was used to solve the common area of the double|robot workspace， and the extreme value theory and search area method were used to the common area boundary. By extracting the curve， the boundary surface and the extreme position of the dual robot cooperation space could be determined. The simulation results showed that the method had the advantages of easy implementation and intuitive spatial expression， and could be applied to any dual|arm robots with other structural forms and arbitrary degrees of freedom to solve similar problems.

关键词：双机器人;协作空间;蒙特卡洛法;极值理论;Matlab仿真

Key words：double|robot;collaborative workspace;Monte Carlo method;extreme value theory;Matlab simulation

中圖分类号：TP242文献标识码：ADOI：10.3969/j.issn.2096-1553.2019.04.015

文章编号：2096-1553（2019）04-0102-07

0 引言

目前，在工业生产制造领域中，双工业机器人协同作业得到了广泛的应用，如双机器人协同焊接、协同搬运、协同喷漆等.多机器人协同作业的工作空间问题是多机器人系统研究中的难点之一[1].双机器人的协作空间代表了机器人的活动范围，它是双机器人工作能力的重要表现[2].协作工作空间的研究，对机器人的机构设计、路径规划、轨迹规划、避碰研究、最佳操作位形研究等，都有相当重要的意义[3-4].

芦俊等[5]采用数值法对双臂智能机器人的协作工作空间进行了分析研究，得出了最佳协作空间，该方法使用几何计算，数据量大、精确度低，相比计算机数据计算存在一定的误差;赵燕江等[6]提出了基于Matlab的机器人工作空间求解方法，该方法简单、快速、准确，可通过 Matlab输出可视化结果，但该方法只针对单一机械臂的工作空间求解;谢生良等[7]采用蒙特卡洛法分析了双臂机器人的工作空间，并采用按列和按角度划分的方法提取协作空间的边界点，此方法提取精度高，较准确，但相对计算量较大.

当前对机器人工作空间的求解多集中在双臂机器人和单个工业机器人上，对于双机器人协作空间的研究很少[7].鉴于此，本文拟在双臂机器人工作空间求解方法的基础上，以双机器人协作系统为参考模型，通过确定D|H参数和求解运动学正解，基于Matlab，利用蒙特卡洛法[8]对双机器人协同工作空间进行分析，按列划分边界点，并对边界点进行曲线拟合，进而求出最佳协作空间，以期为双机器人的动力学分析、协调轨迹规划、机器人本体尺度优化奠定理论基础.

1 双机器人运动学分析

本文以由两个六自由度工业机器人组成的双机器人协作系统为研究对象，该机器人协作系统旨在用于工业生产上协同焊接、铆钉、装配等复杂任务作业.

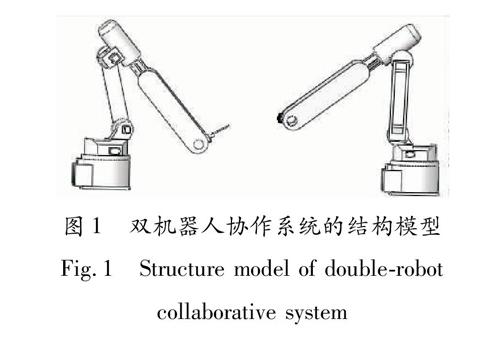
在SolidWorks 2012软件中建立双机器人协作系统的结构模型如图1所示.该系统模型采用主机器人1（左）和从机器人2（右）结构布局，两机器人距离为2L.

工作空间的大小与机器人结构参数有关，若双机器人的工作空间刚好包裹住待加工工件实际大小，即为最佳协作空间的区域.在已知待加工工件尺寸大小的基础上，通过上述方法求解，得出机器人工作空间的大小，可为机器人的选型提供依据，降低机器人购买成本，有效地减少不必要的损耗.

以上所求得的工作空间都是不考虑机器人本身避障情况[11]下所得到的工作空间.

2.3 协作工作空间边界曲线数值计算

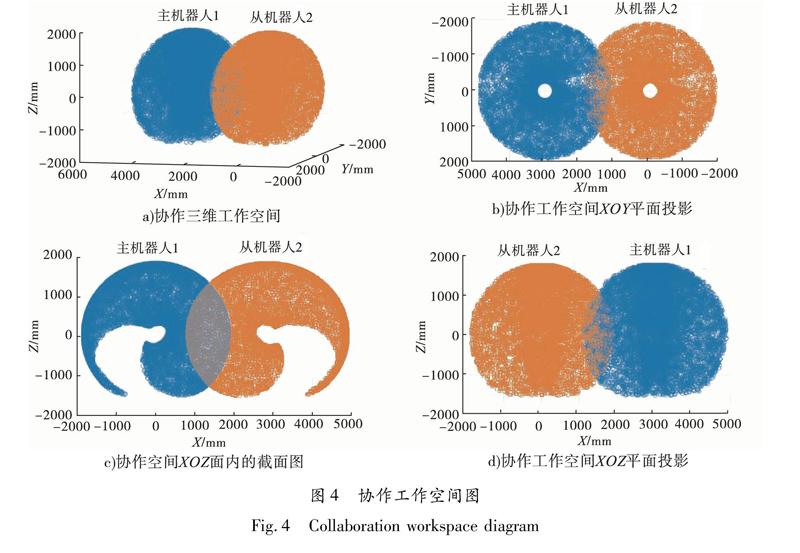
采用极值理论和搜索区域法对协作工作空间边界曲线进行提取.假设机器人工作空间由N个平面组成，每个平面上都至少有一个在一定范围内的蒙特卡洛点，因此只要得到每个平面上点的范围，这些点在面上层层重叠组成的所有点的集合即为机器人工作空间.现对三维图中的内切图图4c）中的双机器人工作空间边界进行边界提取，图中重合部分即为协作工作空间.对机器人协作工作空间边界曲线提取具体步骤如下.

步骤1 设X轴的最大区域为k=Xmax-Xmin，将图4c）所在面沿X轴平均分为N列，设列的宽度为b=k/N，N要无限大，从而确保所提取的边界曲线的精确度.

步骤2 在N个列中，沿着Z轴坐标系搜索所在列的Zmax和Zmin，然后确定它们所对应的坐标极值点.

步骤3 在搜索Zmax和Zmin过程中可能出现空洞：如果在某一列发现两个相邻的点之间的差值远远大于列的宽度b，就表明在此点有空洞出现.此时，这两个相邻的点记为边界点，依次类推，直至搜索到X轴的最大区域k点，得到每列的边界曲线点.

步骤4 依次寻找最近点连接所求的所有边界点，建立边界曲线.

3 数值计算与分析

为验证本文双机器人协作工作空间求解方法的有效性，运用上述求解方法，基于Matlab求解出双机器人工作空间的空间区域和极限位置.6R双机器人D|H参数见表1，两机器人位置距离2L=3000 mm，关节θ4—θ6对末端执行器的姿态有影响，而对执行器末端点位置没有影响，故未计算在内.单个机器人工作空间极限位置和关节变量参数计算结果见表2，由此得到协作工作空间极限位置、主机器人1和从机器人2关节变量参数计算结果见表3.连接所求的所有边界点，得到二维工作空间曲线图，如图5所示，其中的公共区域为双机器人能够到达的区域，即协作工作空间的边界轮廓.

由表3和图5可知，通过求得双机器人协作空间边界图，从而确定机器人工作空间边界极限位置，通过逆解公式即可求得每个极限位置所对应的各个关节角值，具有易于实现、空间表达直观等优点.该双机器人协作工作空间求解方法相比李国栋等[12]运用代数求解方法求解，可以避免求解方程数目多、计算量大、空间表达不直观等不足，并且该方法可应用于其他结构形式和任意自由度的双臂机器人类似问题求解.

4 结语

本文以双机器人协作系统模型为研究对象，根据其D|H参数求出运动学正解，通过Matlab对雙机器人协作运动的工作空间进行求解，并通过极值搜索域法进行协作空间边界曲线的提取与绘制，从而得到双机器人协作空间的公共区域形状和在空间内协作空间的极限位置参数.

仿真结果表明，该方法具有易于实现、空间表达直观等优点，可应用于其他结构形式和任意自由度的双臂机器人类似问题求解，从而为下一步在协作工作空间内研究双机器人协同作业的路径规划、动力学分析、机器人的机构参数优化，以及协作避碰问题奠定理论基础.

参考文献：

[1] 赵大兴，周小明，李九灵.集装箱喷漆机械手工作空间分析与仿真[J].机械设计，2008，25（2）：15.

[2] 曹毅，王树新，邱燕，等.面向灵活工作空间的显微镜外科手术机器人设计[J].机器人，2005，27（3）：220.

[3] 周律，周昱明，汪亮，等.基于蒙特卡罗方法的双臂机器人工作空间分析[J].机械传动，2014，38（6）：85.

[4] 李情，茅健，朱姿娜，等.双机械手协同运动模型及其工作空间分析[J].制造业自动化，2017，39 （11）：44.

[5] 芦俊，池宏勋，席文明，等.双臂机器人的协作空间数值计算方法[J].中国机械工程，2001，12（SI）：125.

[6] 赵燕江，张永德，姜金刚，等.基于Matlab的机器人工作空间求解方法[J].机械科学与技术，2009，28（12）：1657.

[7] 谢生良，刘祚时.双臂机器人工作空间的分析与仿真[J].机械传动，2018，42（6）：139.

[8] GUPTA K C，ROTH B.Design considerations for manipulator workspace[J].Journal of Machanical Design，1982，104（4）：704.