几类转化为双曲线特征三角形的问题的解法

吴峻峰

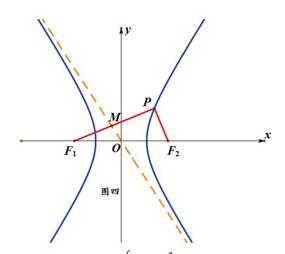
双曲线中很多求基本量的问题涉及的背景可以转化为双曲线的特征三角形问题，运用特征三角形的几何性质解决这类问题思路简洁，运算量小，若能进行合理转化，往往能达到事半功倍的效果。

以焦点在x轴上双曲线为例，常见有如下两种种特征三角形：

本文主要研究图二中的特征三角形，其中A为焦点：

结论1.OA=c，OB=a，AB=b，

结论2.点B坐标

结论3.过F作渐近线的垂线，垂足为A落在准线上;反之，渐近线和准线交点与相应焦点连线与该渐近线垂直。

以上结论均可计算证明，下面我们例举几类可以转化为双曲线特征三角形的问题的模型，体会巧妙结合特征三角形解题的魅力。

一、以准线与渐近线交点为背景的特征三角形问题

根据特征三角形的性质，准线与渐近线交点与相应焦点连线与该渐近线垂直，可以形成特征三角形。

例1.设双曲线的两条渐近线与直线分别交于A，B两点，F为该双曲线的右焦点，若60°<∠AFB<90°，则该双曲线的离心率的取值范围为（      ）

A.B.C.D.

解法1 （代数法）

∵60°<∠AFB<90°

而

解得：

解法2 （几何法）

∵60°<∠AFB<90°，∴45°<∠AOF<60°从而，

二、以圆的切线为背景的特征三角形问题

特征三角形中的垂直关系是可以利用半径为a的圆与过焦点的直线相切构造，所以这类问题都可以转化为特征三角形问题。

例2.过曲线的左焦点F1作曲线C2：x2+y2=a2的切线，设切点为M，延长F1M交曲线C3：y2=2px（p>0）于点N，其中C1、C3有一个共同的焦点，若|MF1|=|MN|，则曲线C1的离心率为

A.B.C.D.

分析：OM即为双曲线的一条渐近线，为特征三角形，而各边长为其两倍

解法1 （代数法）

由抛物线定义AN=2a，可得N点横坐标x=2a-c

在△NF1F2中由面积法可求得N點纵坐标

由N在抛物线上代入坐标化简可得：e4-2e3+e2-1=0，结合b>a求得

此代数方法计算量较大，事实上注意利用特征三角形中结论，可极大简化计算。

解法2 （代数法）

易知M坐标，所以N点横坐标

化为齐次即e2-e-1=0求得 的更充分些，求解过程将更简洁。下面给出两种几何方法：

解法3（几何法）

在△NF1A中，由勾股定理：y2+4a2=4b2，

即4c（2a-c）+4a2=4b2

解法4（几何法）

由Rt△NF1A与Rt△NF1F2N相似可得：

即b2=ac

三、以对称问题及其他几何背景的特征三角形问题

以对称的关系描述特征三角形的垂直关系也是一类重要的模型。

例3.已知双曲线C：的左、右焦点为F1，F2，P为双曲线C右支上异于顶点的一点，△PF1F2的内切圆与x轴切于点（1，0），且P与点F1关于直线对称，则双曲线的方程为

分析：首先由内切圆的性质易知切点（a，0），则a=1.

解法1 （代数法）

设P（m，n），由对称可知：

则所求双曲线方程为

解法2 （几何法）

为特征三角形，各边长是其两倍，有2b-2a=2a.故b=2

除了本文介绍，可以转化为双曲线特征三角形的模型还有很多，值得我们去挖掘。若能准确转化，合理运用性质，对解题的速度和准确率都有很大帮助。对于与本文类似的可以转化为双曲线特征三角形的其它几何背景或椭圆特征三角形的几何背景模型，读者可以自行研究。