二阶控制系统时间响应分析

熊藜 宋刚 胡荣瀚 张元阳

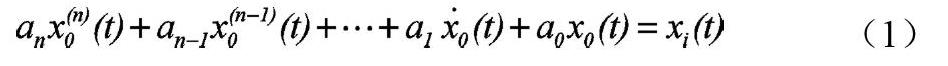
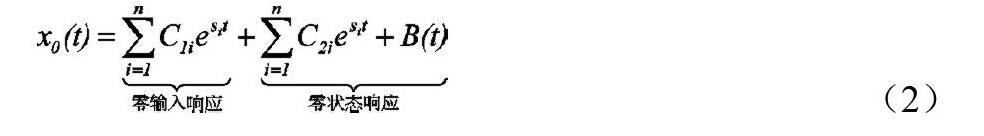
摘 要：基于连续时间系统的响应分析，通过在二阶系统的反馈回路中加入了一阶未知时间常数的微分环节，通过构建传递函数，做出对典型输入信号在不同未知时间常数τ=0，0.0125，0.025下的时间响应曲线。通过Matlab编程求出不同阻尼比ζ=0-2下的二阶系统的瞬态性能指标，进而反推出贴近最优的瞬态性能的反馈时间常数，其值为τ=0.025。最优对二阶系统的稳定性判据方法进行了分析与描述。

关键词：时间响应;瞬态性能;反馈时间常数;稳定性判据

中图分類号：TP271+.2  文献标识码：A  文章编号：1671-7988（2019）12-96-03

Abstract： Based on the response analysis of the continuous time system， the first order unknown time constant differential link was added into the feedback loop of the second order system. The transient performance index of the second-order system with different damping ratios was obtained through Matlab programming， and then the feedback time constant close to the optimal transient performance was derived， and its value was. The stability criterion method for optimal second-order systems is analyzed and described.

Keywords： Time response; Transient performance; Feedback time constant; Stability criterion

引言

工程中，大量的控制系统，尤其是机械系统，都可利用高阶微分方程的原理建立起高阶系统。对于这种复杂的系统，在一定准确度条件下，可以忽略某些次要因素，将高阶系统简化为二阶或一阶系统的串并联的组合。这样便可利用二阶系统的性能指标以及系统偏差的校正，从而做出对高阶系统的分析与研究。为了更好的了解二阶系统的特性，对其做时间响应分析是重要的解决方法。

本文主要对二阶系统的动态性能作时域响应分析和频率特性指标进行分析，从而掌握系统稳定性、响应快速性、响应准确性三者之间的制约关系，对控制系统的设计与分析有重大意义。

1 时间响应及组成

系统的时间响应可从两方面进行分类，根据系统的振动性质可分为自由响应与强迫响应;按系统振动来源可分为零输入响应与零输入响应。

根据系统动力学一般方程表达形式有：

系统的时间响应由两部分组成，即：

零输入响应指在没有输入激励的作用下，仅由初态引起的自由响应。按照求解顺序可先求出零输入响应，再求出零状态响应。零状态响应为无输入时系统初态为零而仅有输入引起系统的响应。本文研究的响应为零状态响应。

2 二阶系统的典型代表性

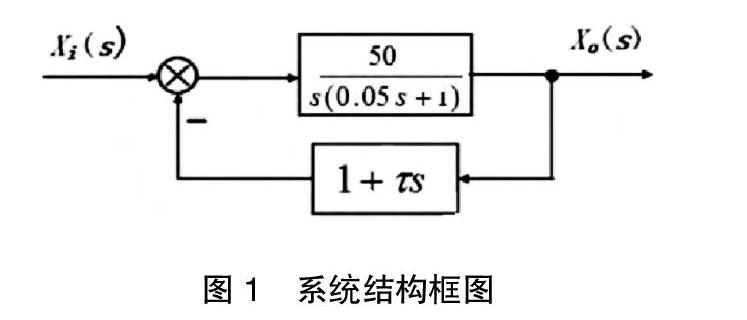
现实条件下二阶系统的典型事例有很多，如RCL电网络系统、具有惯性荷载的液压助力器以及质量-弹簧-阻尼机械系统等。举例假设某系统结构图如图1所示：

该二阶系统中在反馈回路处加入了一阶未知时间常数的微分环节，通过构建传递函数，取不同的时间常数 值，分析输入单位脉冲与单位阶跃信号对系统的影响。求取系统的传递函数为：

其中，运算得出系统无阻尼固有频率值ωn值为31.6s-1，阻尼比ξ值为0.32+15.8τ，τ为时间常数，这里分别取值为0、0.0125、0.025，ωn与ξ是二阶系统的特征参数。

在典型输入信号单位脉冲与单位阶跃的作用下，分别应用Matlab软件中的impulse函数与step函数可以得到系统的单位脉冲响应与单位阶跃响应，响应曲线示意图如图2所示。

通过图2可以看出不同的时间常数τ对单位脉冲响应以及单位阶跃响应有着不同的影响。如此一来，这一组时间常数更加符合系统的性能指标，或者说那组数据对控制系统的三大研究问题，即系统稳定性、响应快速性、响应准确性的综合评价更高，这就需要考虑二阶系统响应的性能指标，从而对比做出判断。

3 二阶系统响应瞬态性能指标

大多数情况下，评价系统的性能指标一般在时域范围内研究。考虑到二阶欠阻尼系统过渡时间的较短，产生单位阶跃输入信号较为容易且与实际情况下输入的信号更加贴近振荡，同时系统在对单位阶跃信号做出的响应可以求出任何输入下的响应等优点，我们对其作进一步分析。

3.1 上升时间、峰值时间与频率调整时间

二阶欠阻尼系统中，反映响应曲线第一次达到稳定值所需要的时间即为上升时间tr;而响应曲线第一次达到峰值的时间称为峰值时间tp。两者在数学关系上有很大的相似性，当阻尼比ξ增大，ωn增大，tr与tp均减小。此外，过渡过程中的x0（t）满足或不等式所需的时间定义为调整时间ts。

3.2 最大超调量与振荡次数

定义最大峰值相对与稳定值的之差的百分量称为最大调整量Mp，即。可见，超调量Mp只与阻尼比ξ有关，而与固有频率ωn无关。由此得出最大超调量的大小直接可以说明系统的阻尼特性。对于振荡次数N，同样是随着阻尼比的增加而减少，其大小也直接反映了系统的阻尼特性。

3.3 不同阻尼比下的时间响应

从白车身弯曲刚度计算公式可看出，影响弯曲刚度的主要是纵梁最大变形量。对于同一台白车身而言，影响纵梁最大变形量的因素有约束方式和驾驶室本身的状态是否安装挡风玻璃。

2 约束方式对白车身刚度的影响分析

2.1 约束方式对白车身扭转刚度的影响分析

白车身扭转刚度试验按照扭矩施加位置的不同可分为前扭转和后扭转。在白车身前悬施加扭矩，后悬固定为前扭转，侧重考核白车身后部结构的抗扭变形能力，反之则为后扭转。对于商用车而言，认为白车身前扭转刚度比后扭转刚度更值得关注。本文通过白车身前扭转台架试验为例来探讨约束方式对白车身扭转刚度的影响。

选取某款商用车车型白车身1台，在白车身静刚度试验台上进行扭转刚度试验，试验时选取常用6种约束方式（见表1）进行试验，每种约束试验进行3次，记录试验数据。为保证数据测量的准确性，毎种约束方式刚度试验完成后将驾驶室拆除再重新安装。

为保证测量数据的可比性，每组试验施加相同扭矩，刚度值计算按照1.1进行，每种约束取3组试验刚度平均值作为最终刚度值，试验数据详见表2所示。

通过对表2的数据分析可知：不同约束方式下扭转刚度值偏差在3%以内，该误差可认为是白车身安装引起的。故认为约束方式对商用车白车身扭转刚度基本无影响。在进行试验时，为方便与CAE对比和固化试验方法，通常选取约束1。

2.2 约束方式对白车身弯曲刚度的影响分析

选取某款商用车车型白车身1台，在白车身静刚度试验台上进行弯曲刚度试验，试验时选取常用2种常见约束方式（见表3）进行试验，毎种约束试验进行3次，记录试验数据。为保证数据测量的准确性，每种约束方式刚度试验完成后将驾驶室拆除再重新安装。

为保证测量数据的可比性，每组试验施加相同加载力且加载面积和位置一致，刚度值计算按照1.2进行，每种约束取3组试验刚度平均值作为最终刚度值，试验数据详见表4所示。

通过对表4的数据分析可知：不同约束方式下弯曲刚度值偏差为4.8%，该误差可认为是白车身安装引起的。故认为约束方式对商用车白车身弯曲刚度基本无影响。在进行试验时，为方便与CAE对比和固化试验方法，通常选取约束方式1。

3 挡风玻璃对白车身刚度的影响分析

白车身刚度测量时有安装挡风玻璃和未安装挡风玻璃两种状态，未安装挡风玻璃的刚度主要用于与标杆车的刚度数据作对比，指导白车身钣金件设计，安装挡风玻璃的刚度与驾驶室总成的刚度更加接近，测量也十分必要。

3.1 挡风玻璃对白车身扭转刚度的影响分析

这里以白车身前扭转刚度试验为例来探讨挡风玻璃对白车身扭转刚度的影响。

选取某3款商用车车型白车身各1台，在白车身静刚度试验台上进行扭转刚度试验，每组试验进行3次，记录试验数据。为保证数据测量的准确性，未安装挡风玻璃刚度试验完成后，拆除白车身安装挡风玻璃后重新安装于试验台上进行试验。

为保证测量数据的可比性，每组试验施加相同扭矩，刚度值计算按照1.1进行，每种状态取3组试验刚度平均值作为最终刚度值，试验结果详见表5所示。

通过对表5数据分析可知，安装挡风玻璃与不安装挡风玻璃的扭转刚度值存在着接近2倍的关系，安装挡风玻璃后白车身扭转刚度提升幅度可高达111%。说明挡风玻璃对商用车白车身扭转刚度贡献大。

3.2 挡风玻璃对白车身弯曲刚度的影响分析

这里以在驾驶室主副座椅处加载的弯曲工况为例来探讨挡风玻璃对白车身弯曲刚度的影响。

选取某3款商用车车型白车身各1台，在白车身静刚度试验台上进行弯曲刚度试验，每组试验进行3次，记录试验数据。为保证数据测量的准确性，未安装挡风玻璃刚度试验完成后，拆除白车身安装挡风玻璃后重新安装于试验台上进行试验。

为保证测量数据的可比性，每组试验施加相同加载力且加载面积和位置一致，刚度值计算按照1.2进行，每种状态取3组试验刚度的平均值作为最终刚度值，试验结果详见表6所示。

通过对表6数据分析可知，安装挡风玻璃与不安装挡风玻璃的弯曲刚度值较接近，安装挡风玻璃后白车身弯曲刚度提升幅度不超过5%。说明挡风玻璃对商用车白车身弯曲刚度的贡献较小，是否安装挡风玻璃对白车身弯曲刚度几乎无影响。

4 结语

本文从约束方式和擋风玻璃两个方面对商用车白车身刚度的影响进行了研究，并进行大量的试验。从试验数据的分析结果可知：

（1）约束方式对商用车白车身扭转刚度和弯曲刚度基本无影响，刚度偏差值保持在5%以内。在进行刚度试验时，为方便与CAE对比和固化试验方法，通常选取对角约東方式。

（2）挡风玻璃对商用车白车身扭转刚度贡献大，刚度提升幅度可高达111%;挡风玻璃对商用车白车身弯曲刚度贡献较小，刚度提升幅度不超过5%，认为挡风玻璃对商用车白车身弯曲刚度几乎无影响。

本文得出的结论在一定程度上能够指导白车身刚度试验和修正白车身设计，但因对白车身刚度影响因素考虑有限，在后续的研究中应多考虑一些因素，更加全面的对白车身刚度影响因素进行研究分析。

参考文献

[1] 日本自动车技术会编;中国汽车工程学会组译.汽车工程手册3： 造型与车身设计篇[M].北京：人民交通出版社，2010.12.

[2] 于国江，汽车白车身刚度仿真分析与检测技术要求[D].硕土学位论文，湖南大学，2014：1-3.

[3] 黄天浮，黄金陵，汽车车身结构与设计[M].北京：机械工业出版社， 2012.6.

[4] 汽车工程手册编辑委员会.汽车工程手册：试验篇[M].北京：人民交通出版社，2000.12.

[5] 王进，谭继锦等.某轻型载货车白车身刚度和强度试验分析[J].农业装备与车辆工程：2014（01）：36-39，58.