朴素贝叶斯及其在乳腺肿瘤诊断中的性能研究
2019-10-21赵闻平陈旭赵倩
赵闻平 陈旭 赵倩
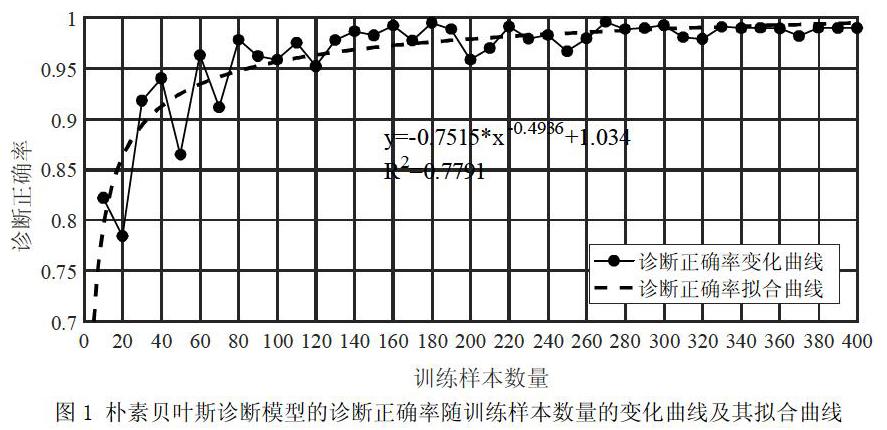
【摘 要】目的:阐释朴素贝叶斯在乳腺肿瘤诊断中的应用原理,同时分析其诊断性能的变化特征;方法:把已经确诊的500个乳腺肿瘤病例分为训练样本集合与检验样本,其中前400个样本作为训练样本集合,后100个样本作为测试样本。实验过程中,随机从400个训练样本集合中选择一定数量的子集作为一次实验过程中的训练样本以用于训练朴素贝叶斯诊断模型,然后用100个测试样本来检验模型的诊断性能。结果:朴素贝叶斯诊断模型诊断正确率p与训练样本数量N之间满足指数函数p=-0.7515*N-0.4936+1.034(判定系数R2=0.7791)的关系;模型的诊断性正确率与训练样本数量之间是正相关关系;当训练样本数量达到一定数量之后,朴素贝叶斯诊断模型的诊断性能趋于稳定,诊断正确率的均值为98.45%、标准差为0.88%。结论:基于朴素贝叶斯的诊断模型作为辅助医生进行乳腺肿瘤诊断的工具具有很好的推广应用潜力。
【关键词】朴素贝叶斯;乳腺肿瘤;机器学习;医学诊断模型
【中图分类号】R18 【文献标识码】A 【文章编号】1672-3783(2019)12-0019-02
乳腺肿瘤是女性健康的重要危害因子之一[1],早诊断、早发现是当前医疗水平下唯一能降低乳腺肿瘤致死率的唯一方法。机器学习是研究如何让计算机程序来模仿人类学习与决策的一种新兴交叉学科[2], 通过机器学习的方式对癌症进行研究,可以通过对现有的癌症病例样本进行学习,使计算机具有一定的决策能力后对未知的癌症病例进行智能判断和评估,可以作出比医生更为准确的智能决策的同时,还能降低因人为因素而造成的误诊、漏诊[3-6],对乳腺肿瘤死亡率的降低有着极其重要的现实意义[6]。本文将以乳腺肿瘤诊断为例,系统性地阐释朴素贝叶斯在医学诊断中的应用原理,并测试其在不同样本数量下诊断性能的变化特征,并对其诊断性能的变化特征进行深入探讨,以期得到更普适、更具推广性的结论。
1 方法与数据
1.1 朴素贝叶斯
朴素贝叶斯(Naive Bayes)发源于古典数学理论,是基于贝叶斯定理与特征条件独立假设的方法,有着坚实的数学基础[7]。朴素贝叶斯方法的输出结果是概率性的,即它会计算出某个给定的样本属于每个类别的概率,然后以概率最高的类别作为分类或者诊断的结果。比如在乳腺肿瘤诊断中,朴素贝叶斯方法会计算出某个病例分别属于良性和恶性的概率,并把概率最大的作为诊断结果。朴素贝叶斯获得这些概率的方式是借助于贝叶斯理论[7],贝叶斯理论的核心思想是:根据一个已发生事件的概率,计算另一个事件的发生概率。贝叶斯理论从数学上可以表达成这样:
1.2 数据与实验设计
为了检验朴素贝叶斯诊断模型在训练样本数量不同的情況下其诊断性能的变化特征(也就是朴素贝叶斯诊断模型的稳定性),本研究设置了系列实验。实验过程中,我们不断变化训练样本的数量,样本数量从10个到400个依次变化,间隔大小为10个,即系列实验中:第1轮实验所用的训练样本的数量为10个,第2轮实验所用的训练样本的数量为20个,依次类推,最后1轮实验所用的训练样本的数量为400个。每轮实验所用的训练样本都是从训练样本集合中随机抽取出来的,而且每轮实验都重复开展50次(注:这50次实验中,每次实验所用的训练样本数量是一样的,但是每次实验的训练样本是从前400个病例中随机挑选的)以减小因训练样本的差异性所带来的诊断模型的不确定性(即蒙特卡洛思想[8]),取这50次实验所得到的50个诊断正确率值的均值当作本轮实验的诊断正确率。同时,所有实验中,测试样本的数量固定在100个不变,以观察训练样本数量变化的情况下诊断模型的诊断性能的变化特征。实验平台为Windows10操作系统,编程环境为Matlab2016a。
2 结果与分析
通过对朴素贝叶斯模型的诊断正确率与训练样本数量进行函数拟合,拟合结果表明两者之间符合如下的指数函数关系:
3 讨论与结论
朴素贝叶斯诊断模型是一种经典的医学诊断模型,用于判别样本属于特定类的概率(比如在本文中用于诊断患者的乳腺肿瘤属于良性或恶性的概率)。通过本研究我们发现朴素贝叶斯诊断模型的诊断正确率与模型训练样本数量之间存在很高的正相关关系,随着模型训练样本数量的增加,朴素贝叶斯模型的诊断正确率也随之得到提高。
此外,尽管朴素贝叶斯方法有一个根本的前提条件,即:假设特征条件独立。这一假设尽管可以简化计算,但是在实际应用中通常很难完全满足,在这种情况下,模型的分类或诊断性能就有可能受到影响。然而,在本研究中我们发现,即便乳腺肿瘤的10个量化特征,即细胞核直径、质地、周长、面积、光滑度、紧密度、凹陷度、凹陷点数、对称度、断裂度之间可能不会完全满足朴素贝叶斯方法所需的条件独立性假设,但是本研究中通过大训练样本所得到的朴素贝叶斯诊断模型依然展现出了非常高的诊断正确率(诊断正确率的均值达到了98.45%),而且表现出了稳定的诊断性能(标准差为0.88%)。
最后,鉴于在本研究中朴素贝叶斯诊断模型所表现出来的优秀的诊断性能,因此,在有大量训练样本的前提下,基于朴素贝叶斯方法的医学诊断模型作为辅助医生进行医学诊断的一种智能高效的诊断工具,具有很好的推广应用潜力。
参考文献
[1] 左婷婷, 陈万青. 中国乳腺癌全人群生存率分析研究进展[J]. 中国肿瘤临床, 2016, 43(14):639-642.
[2] Ethem Alpaydin. Introduction to Machine Learning(3rd Edition)[M]. Prentice Hall of India,2014.
[3] 袁前飞. 基于支持向量机的癌症诊断研究[D]. 重庆大学, 2007.
[4] 王琼芳. B超图像的乳腺肿瘤计算机辅助诊断系统研究[D]. 四川师范大学, 2009.
[5] 刘奕. 基于机器学习的癌症诊断方法研究[D]. 湖北工业大学, 2017.
[6] 霍双红. 基于机器学习的乳腺肿瘤识别[D]. 中北大学, 2017.
[7] Horimoto K. Bayes Rule[M]. Springer New York, 2013.
[8] 尹增谦, 管景峰. 蒙特卡罗方法及应用[J].物理与工程,2002,12(3):45-49.