一种激光导引星自适应光学系统中激光上行到达角起伏测量方法的研究*
2019-10-21李语强
黄 凯,曹 进,肖 啸,李语强
(1. 乐山师范学院物理与电子工程学院,四川 乐山 614000;2. 中国科学院云南天文台, 云南 昆明 650011)
自适应光学系统需要足够亮度的导引星作为波前探测的信标,可以利用目标本身作为信标,也可以在目标的等晕区范围内寻找一颗合适亮度的自然导引星作为信标,这样的系统称为自然导引星自适应光学(NGS-AO)系统。1985年,文[1]提出将人造激光导引星应用于天文自适应观测。激光导引星发射在目标的等晕区范围内,用于自适应光学系统的波前探测,这样的系统称为激光导引星自适应光学(LGS-AO)系统。理想的人造信标需要具有足够亮度,并且与目标的相对位置稳定。目前激光导引星虽然能够达到满足天文观测的亮度(Keck II望远镜配备的下一代激光系统能够在天顶角小于15°范围内制造相当于R波段7.5等亮度的钠导星[2]),但是并不稳定,还需要在倾斜等晕区范围内寻找一颗恒星为其校正波前倾斜。如图1,激光上行光路受大气湍流的影响,瞬时的激光信标与激光发射光轴有一定的偏移,这导致自适应光学系统波前传感器探测到的激光导引星波前倾斜量失真。
对激光导引星波前倾斜测量方法的研究最早由FOY等人在20世纪90年代展开[3]。1995年,文[4]提出利用辅助望远镜发射激光,主望远镜从侧面探测激光导引星的方法,并于2000年报道了实验结果:在西班牙Calar Alto天文台利用3.6 m望远镜发射激光,2.2 m望远镜从侧面探测激光束,并借助一颗自然导引星成功探测到了目标的一维波前倾斜[5]。2000年,文[6]提出利用主望远镜发射激光,辅助望远镜探测激光投影的方法,对辅助望远镜中成像的激光带使用统计平均算法得到激光上行的波前倾斜。1997年,文[7]对激光导引星自适应光学系统的波前倾斜测量进行理论上的分析,并对多种辅助望远镜方案进行了对比和分析。2000年开始,中国科学院云南天文台和中国科学院光电技术研究所合作展开激光瑞利导引星项目的实验研究[8],同时开始关注激光导引星用于大气波前倾斜测量的问题[9-10],并于2014年利用云南天文台1.2 m望远镜为主望远镜,25 cm望远镜为辅助望远镜实验验证了统计平均算法对于激光导引星波前倾斜测量的有效性[11-12]。2016年,文[13-14]详细分析了倾斜 “互补” 假设的应用条件,并提出一种非倾斜 “互补” 条件下基于多层层析技术的激光导引星波前倾斜探测方法。2016年,文[15]提出一种基于涡旋光束的激光导引星,可以在空中形成一个相比高斯光束更稳定的人造信标以解决激光导引星波前倾斜难以探测的问题,研究结果表明,当旋涡光束拓扑电荷数等于10时,激光上行抖动方差相比高斯光束减小31%。
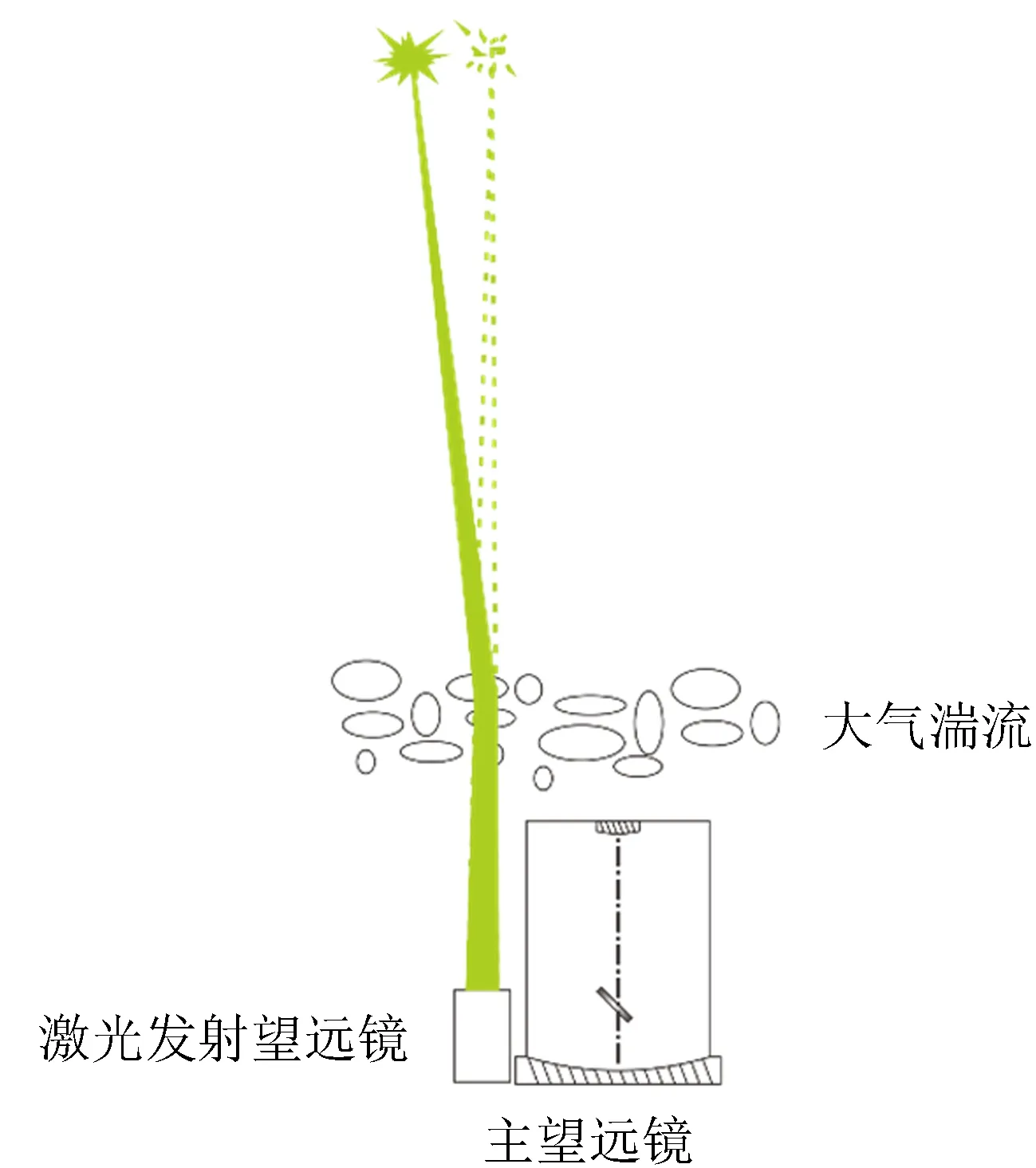
图1 激光导引星受激光上行大气湍流的影响
Fig.1 Laser guide star is affected by laser upward atmospheric turbulence
本文提出一种基于望远镜子孔径探测的波前倾斜测量方法,利用优选算法从子孔径探测数据中分离出激光上行光路的到达角起伏。该方案有别于文[13]提出的多层层析方法,且只需要一颗激光导引星即可获得稳定的人造信标。同时,可以有效地避免辅助望远镜方案中由辅助望远镜跟踪、指向等问题引入的探测困难。
1 激光导引星波前倾斜测量方法的系统布局
基于望远镜子孔径探测的激光导引星波前倾斜测量方法系统结构如图2。激光由发射望远镜发射并在高空形成人造信标,信标光经大气湍流传输进入主望远镜。波前畸变的信标光首先通过波前校正系统(由倾斜反射镜MT和可变形反射镜MD组成),再利用分光反射分别进入成像系统和波前探测系统。假设忽略激光导引星和观测目标之间的大气湍流的影响,如果信标足够稳定,可以通过对信标波前的探测实时校正目标的波前畸变,以实现对目标的高分辨率成像。因为激光上行受大气湍流的影响,所以瞬时的激光信标与激光发射光轴有一定的偏移,这导致望远镜接收的波前畸变中有一个附加的倾斜量。波前信号由3部分组成:激光信标下行整体倾斜、波前高阶畸变信号、激光上行附加倾斜。如果不校正激光上行附加倾斜,目标在相机中的像不稳定,难以实现长时间曝光。本文提出一种算法,可以从波前传感器中分离信标上行抖动信息,由控制器生成信号控制激光发射望远镜的快速倾斜镜以稳定激光信标。系统中波前探测器将输出3路信号分别控制可变形反射镜MD、接收望远镜端倾斜反射镜MT和发射望远镜端快速倾斜镜。
2 波前倾斜提取方法
图3为激光导引星子孔径测量方法示意图。接收望远镜分割为排列整齐的子孔径,黄色部分为子孔径接收的信标光的下行光路,图中只画出了部分子孔径的光路作为参考,绿色部分为激光上行光路。可以看出,激光束由发射上行到接收下行共经历了两次大气湍流。每个子孔径范围内的波前倾斜使微透镜的聚焦光斑产生横向漂移,测量光斑中心在两个方向上相对于用平行光标定的基准位置的漂移量,可以求出各子孔径范围内的波前在两个方向上的平均斜率θ。

图2 系统结构图
Fig.2 Schematic diagram of system structure
任意子孔径i探测到的波前倾斜量θi都是由激光上行抖动量θup和下行子孔径倾斜量θdown,i之和构成,即
θi=θup+θdown,i.
(1)
若随机选取N个子孔径(图3中红色标记子孔径),对这N个子孔径探测到的波前倾斜量进行统计平均:
(2)
对于每一个子孔径,虽然下行光路经历的湍流不同,即θdown,i不同,但是由于激光上行引起的抖动θup是相同的,所以(2)式可以改写为
(3)
或:
(4)
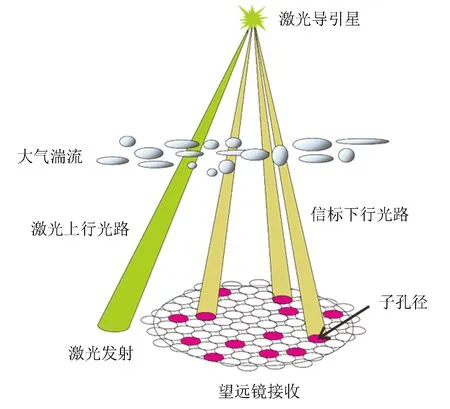
图3 激光导引星子孔径测量方法
Fig.3 Laser guide star tip-tilt measurement method based sub-aperture

(5)
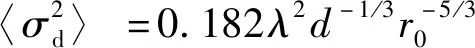
(6)
(7)
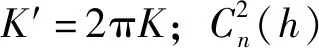

3 数值计算结果分析
利用(5)式对随机选取的子孔径计算其算法误差的大小。如图4,在望远镜口径范围内选定任意N个子孔径,对于任意两个子孔径之间的归一化倾斜相关系数由(6)式计算得出,其中子孔径之间的距离由子孔径之间的坐标关系给出,大气相干长度由下式计算:
(8)
这里采用Hufnagel湍流结构常数剖面模型:
(9)
以上两式中,β为天顶角;v为风速,是与海拔有关的变量。为了简化计算,天顶角设为0°,风速设为常数。(6)式~(9)式将归一化倾斜相关系数与大气相干长度r0联系起来。
将归一化倾斜相关系数代入(5)式可计算出算法误差。多次随机选择获得仿真结果见图5,图中描述了基于子孔径优选算法的误差随子孔径数量的关系。其中,图中给出的两条参考线分别是子孔径倾斜误差和望远镜全口径倾斜误差,由下式[17-18]计算得到:
(10)
其中,D为孔径的直径。仿真结果显示,当仅选择1个子孔径时,缺乏统计效应,算法误差等于子孔径倾斜误差。随着子孔径数量增多,统计效应显现,算法误差下降。对于1 m口径的望远镜,选择的子孔径数量在10~20个时算法误差最小,对于3 m口径的望远镜,选择的子孔径数量在20~50个时统计误差最小。当选择的子孔径数量继续增多时,误差将接近望远镜全口径时的倾斜误差,这是因为选择的子孔径数量越多,对望远镜全口径波前的采样越密,这也就越接近望远镜全口径的波前倾斜。

图4 子孔径选择示意图,图中大圆表示望远镜口径,实心小圆表示子孔径
Fig.4 Schematic diagram of subaperture selection. The large circle represents the telescope aperture, while the small circle represents the selected subaperture
望远镜口径为1 m时,最小算法误差下降为望远镜全口径倾斜误差的70%,当望远镜口径为3 m时,最小算法误差下降为望远镜全口径倾斜误差的50%。从图5可以看出,最小算法误差相对于望远镜全口径倾斜误差的下降程度并不随大气湍流(由r0表征)的变化而变化,而只与望远镜口径有关,望远镜口径越大,算法误差相对于全口径倾斜误差的下降越多。仿真结果显示,当望远镜口径为10 m时,最小算法误差下降为望远镜全口径倾斜误差的33%。这种情况下,如果激光扩束到1 m发射,激光上行抖动误差相比于未校正时减小78%。
4 结 论
本文提出的子孔径优选算法,当从望远镜子孔径中随机选取部分子孔径时,各子孔径之间受大气湍流的影响相对独立,每个子孔径范围内的波前倾斜使微透镜的聚焦光斑产生的漂移量也是相对随机的。用平行光标定的基准位置为0点,多个随机漂移量的平均值将接近0值,而且随着子孔径的数量增加越接近0值。但是随着选择的子孔径数量继续增加,各子孔径之间受大气湍流影响的独立性下降,导致各子孔径的平均值更接近全口径的波前倾斜量。仿真结果表明,选择适当的子孔径数量做统计平均,可以有效地降低信标下行受大气湍流波前倾斜的影响,再由(4)式可以获得激光上行光路的到达角起伏信息,这将用于对激光导引星发射系统的校正,从而获得更加稳定的激光导引星。随着望远镜口径的增大,统计平均算法引入的相对误差越小,当望远镜口径为10 m时,算法误差仅为望远镜全口径倾斜误差的33%。

图5 倾斜测量的算法误差随选择的子孔径数量的变化关系
Fig.5 Algorithm error of tilt measurement varies with the number of selected subapertures
