基于SVM和BP神经网络的金属收得率的预测模型

叶宇成，刘 青，凌佳杰，胡 艳，陈光宇

（南京工程学院电力工程学院，江苏 南京 211167）

钢铁产业是我国工业的重要组成部分，也是国家经济建设的重要支柱。本文对炼钢过程的一个重要环节即脱氧合金化进行研究。基于脱氧合金化的历史数据，分析元素收得率影响因素，在预测模型的基础上结合成本优化模型，求解最优的成本及配料方案。因此，炼钢过程中的脱氧合金化的优化成为了各大钢铁企业提高竞争力要解决的重要问题。脱氧合金化的配料方案优化将不仅能保证钢水质量，还能合理优化投入的合金配比，同时最大限度地降低合金钢的生产成本,对于企业的经济效益和能源的高质量生产都具有重要的意义[1，2]。

1 脱氧合金化模型基础

脱氧合金化[1]要求在出钢过程中，根据钢种要求加入一定量的合金料,使钢水达到规定的脱氧程度。脱氧的同时,还要使钢水中硅、锰及其他元素的含量符合规程要求,以达到合金化的目的。脱氧合金化的反应方程为：

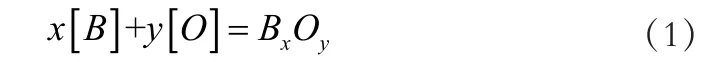
其中，O为氧元素；B为加入的合金元素，包括Si-Al-Ca、Si-Mn、Fe-V、Fe-Mn合金等。

此外，合金元素收得率计算公式为：

合金元素收得率必须估算准确,才能确保生产的钢种达标。然而,合金收得率与诸多影响因素有关,需要具体情况具体分析。

Step1：异常数据的处理

历史数据有部分转炉终点温度为0℃，根据文献[3]可知，0℃的转炉终点温度为异常值，需要进行数据修正。本文通过SPSS的EM算法对这种异常值进行分析和替代。

本文采用SPSS的EM的算法流程如下：

（1）去掉转炉终点温度为0℃的数值，对历史数据进行初始化，估计未知参数的期望值。

（2）重估分布参数，使数据的似然性最大，给出未知变量的期望估计，重复直到收敛。

Step2：各元素收的率的计算

先计算脱氧合金化前后四种钢号各元素的重量百分比，并绘制出相应的曲线图。

2 基于BP神经网络的模型

本文中，输入层与隐含层之间的传递函数我们选用S型函数，其表达式为：

其中，x表示对该神经元的输入，将神经元的输入范围(-∞,+∞)映射到(0,+1)区间上，以利于BP算法训练神经网络。

本文分别对不同钢种的C、Mn元素进行元素收得率的预测，用前一部分的历史数据作为BP神经网络的训练数据，作为输入变量迭代到预测模型中，再用后一部分的数据作为检验数据，从而得到合金收得率的预测结果。

C、Mn元素收得率的预测值与实际值都存在一定偏差，但基本能反映合理的预测结果；综上，该模型预测出的收得率具有一定的参考价值[3,4]。

3 支持向量回归机预测模型的建立

本文我们利用支持向量回归机分别对C、Mn两种元素的不同钢种进行收得率的预测，将前面一部分的数据作为训练样本，其他数据用来检验最优分界面的拟合度。

设支持向量机的线性回归函数为：

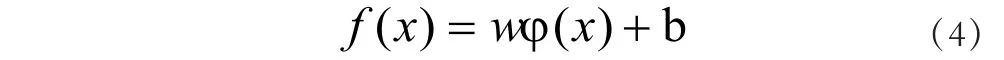
其中，φ(x)为非线性映射函数，它把样本空间映射到一个高维特征空间，我们将在这个高维空间中寻找输入变量和输出变量之间的关系。w为超平面的权值向量，b为偏置向量。

为了得到稀疏解,提高对测试样本的计算速度,我们定义为线性不敏感损失函数，得到一个以函数的最小化为特征的解，从而得到最小解，进行可靠泛化界的优化。

我们引入Largrange函数，并将它转化为对偶形式，式子如下：

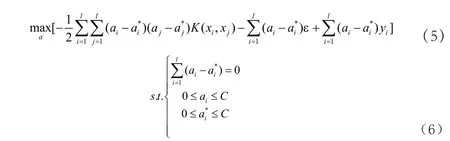
由于径向基函数一方面（RBF函数）可以将数据样本量映射到高维空间，另一方面它比多项式核函数的参数更少，减小模型的复杂性并加速模型求解，故在预测模型的训练中，本文选择径向基核函数来作为核函数。式（6）中ai为引入的Largrange系数；C为惩罚因子，其效果为控制错分样本惩罚。求解上式，可得最优解ai和a向量，进而可求出w*和b*，可得到最优的回归函数为：

本文通过MATLAB的支持向量机工具箱LIBSVM中的SVMTRIN函数，可以得出误差最小的相应参数。在得到最佳参数之后，再使用SVMPREDICT函数来求解出相应的预测值。

基于上述模型，本文使用MATLAB求解出该模型的支撑向量，再将其乘以相应的系数，救可以求得回归系数w和截距项b。进而，用前一部分的数据样本对支持向量回归机进行训练，再用后一部分的数据样本进行测试，从而得到合金收得率的预测结果。我们分别对不同钢号的C、Mn元素进行预测，以下展示其中钢号HRB400D的C元素收得率的预测结果。

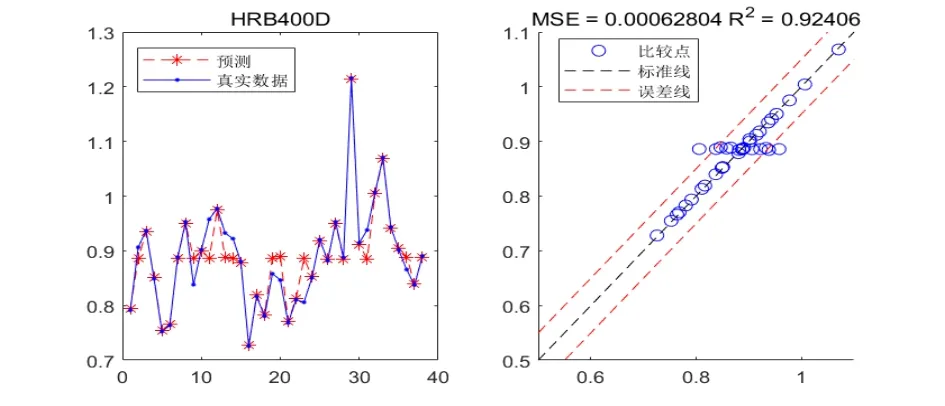
图1 HRB400D钢的C元素收得率预测曲线图和预测值与实际值的比较图

4 模型的拟合精度检验以及对比

为了检验该模型的拟合精度，我们利用均方误差MSE和拟合优度R2来校验预测结果的准确性。其计算公式如下：

同样，我们利用均方误差E和拟合优度R2来观察预测结果的准确性。利用MATLAB求解出的均方误差，将BP神经网络和支持向量回归机的预测结果进行对比。

表1 两种方法的误差比较

均方误差越小、拟合优度越接近于1，则表明该预测结果越准确。

通过观察，我们发现，从大体上来看，为了探究BP神经网络拟合优度波动较大的原因。

由此，我们可以得出以下结论：①支持向量回归机的均方误差比BP神经网络小。支持向量回归机的拟合优度保持在0.86～0.99之间，而BP神经网络的拟合优度波动比较大，在0.1～0.9之间。②支持向量回归机的预测结果比BP神经网络更准确，利用支持向量回归机来进行预测收得率，可靠性更高。③BP神经网络适合较少样本数据的预测，在该情况下，其预测结果的准确性较高。支持向量回归机具有普适性，对于不同数量的样本数据预测，其结果都有较高的准确性。

5 结语

建立的支持向量回归机模型，可以很好地表征数据间的深度联系。它所预测出的结果均方误差较小，拟合优度较高，该模型可靠性很高。用BP神经网络和支持向量回归机两种方法进行预测。两种方法进行比较后，得到了更精准的结果，且总结出了这两种方法的不同的适用情况。本文的缺点在于，附件所提供的有效数据较少，在支持向量回归机的训练过程中，数据量对模型的精度存在一定的限制。如果存在更多的数据，训练所得结果会更加贴近实际。