从演化密码到量子人工智能密码综述
2019-10-21王宝楠张焕国
王宝楠 胡 风 张焕国 王 潮,3
1(特种光纤与光接入网重点实验室,特种光纤与先进通信国际合作联合实验室,上海先进通信与数据科学研究院,上海大学 上海 200444) 2(密码科学技术国家重点实验室 北京 100878) 3(鹏城实验室量子计算中心 广东深圳 518000) 4(武汉大学国家网络安全学院 武汉 430079)
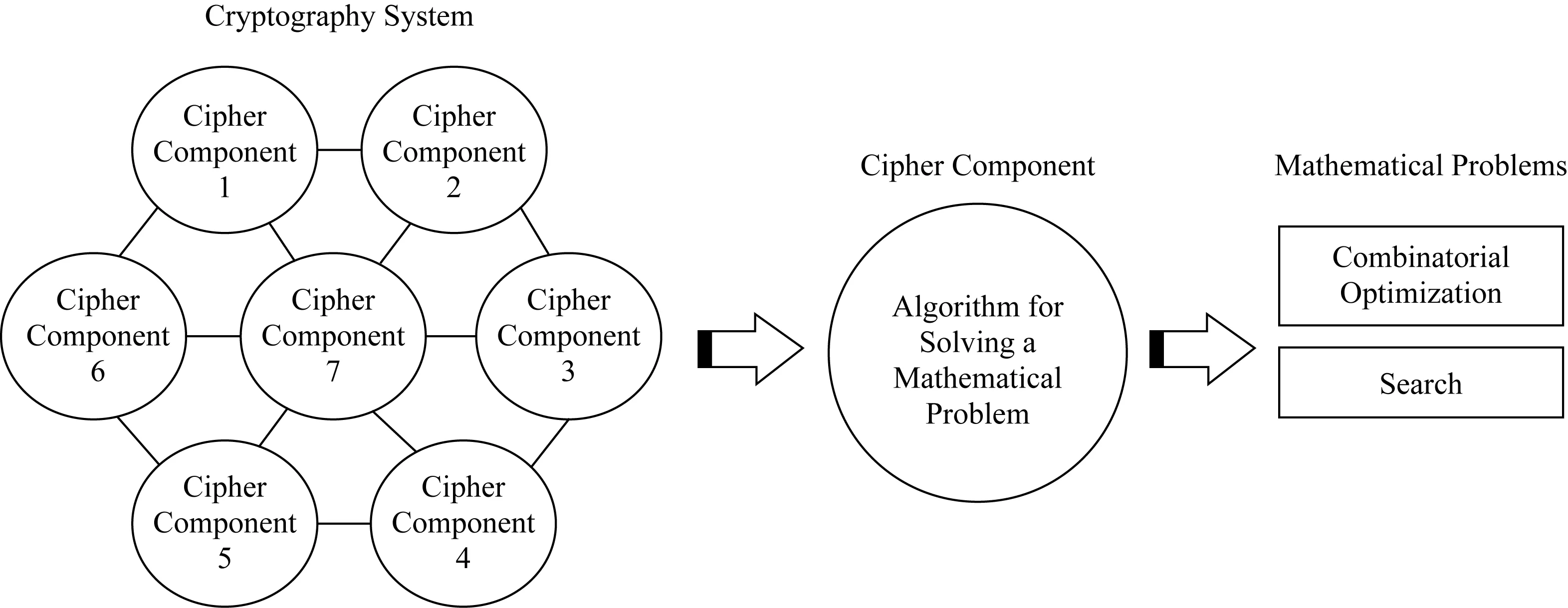
Fig. 1 Relationship between cryptosystem, cryptographic components, and mathematical problem图1 密码系统、密码部件和数学问题的关系
演化算法是一种模拟生物演化过程与机制求解优化问题的一类自组织、自适应的随机搜索算法[1-2].这类算法具有比数学规划方法更大的优越性,它已经成为人工智能领域的研究热点,在解决组合优化和搜索问题方面,如城市旅行商问题[3]、装箱问题[4]、背包问题[5]等取得了较大的成果.
演化算法的引入并非重新设计甚至替代已有密码系统,其本质是在解决无法基于数学理论构建的科学问题求解,而且结合已有的先验知识处理难题,相比传统设计方法更具优势,演化算法已在优化设计、学习和博弈等多个领域取得成功[2].
与国外学者仅考虑演化算法在加解密算法的密码部件应用不同,中国学者将密码学与演化计算结合起来,借鉴生物进化的思想,独立提出演化密码的概念和用演化计算设计密码的方法,采用演化计算解决密码设计与分析中的搜索和优化问题,得到可变渐强的密码,有望成为已有密码分析和设计方法的一种增强手段.
如图1所示,一个密码系统通常由多个密码部件构成的,每个密码部件包含解某个数学问题的算法.倘若解决某个密码部件的数学问题属于组合优化或搜索范畴,那么该密码部件就可以尝试引入演化算法,提高该密码部件的实现效率.
国内外的研究进展表明,演化密码已经在对称密码和非对称密码领域均取得了实际成果,涉及密码分析和设计的诸多领域,从加解密算法的密码部件设计拓展到了密码协议的设计分析.
从演化思想的随机性探索角度出发,量子人工智能提供了一种新的、不同于传统的量子计算模式.典型的量子人工智能算法D-Wave量子计算机原理的量子退火算法,其独特的量子隧穿效应可克服传统搜索算法易陷入局部极值点的缺陷,在密码设计和分析领域实现对演化密码的进一步拓展.
1 演化计算的概念
演化算法和演化计算的概念是什么?1999年Millan给出了演化计算的一种定义——演化计算就是模拟生物演化过程或社会性行为建立模型来解决问题的方法[6].他从生物学和社会行为学角度提炼出演化计算的概念,指明了演化算法是一种模型.但我们认为这一定义还不够全面,因为常见的模拟退火算法与生物体或社会行为并没有什么关系,但通常人们愿意将其作为演化算法的一种.
2002年武汉大学的张焕国教授等人[1]给出了一个比较全面和概括性的定义——演化计算就是基于自然界发展规律而提出的一种通用的问题求解方法.与Millan的定义相比,他将出发点扩大到了自然界,涵盖了生物学和社会行为学,也涵盖了模拟退火算法所在的物理学.
我们认为:演化算法不是一种具体的算法,而是一种通用模型,符合并具有演化特征的算法,都可以设计成演化算法,如常见的蚁群算法、遗传算法、模拟退火算法、以及量子人工智能算法如量子退火算法等,它们所获得的结果总是在不断地迭代中趋向最优.演化算法和仿生算法、人工智能算法在局部概念上具有相似性,容易使人混淆它们之间的关系.与仿生算法、人工智能算法相比,演化算法的概念出现较晚,它实际上是对已知人工智能算法的一种分类,它与人工智能算法之间是包括与被包括的关系.另外,大部分仿生算法,如遗传算法、蚁群算法、细胞自动机等,都具有演化的特征,并且大部分仿生算法的设计目的是为了解决搜索和组合优化问题,这一点与演化计算的目标很相似.因此,大多数仿生算法本身属于演化算法或能够改造成为演化算法,演化算法和仿生算法之间是继承和被继承的关系.
这里我们给演化计算下的定义是——演化计算就是模拟自然界发展规律建立模型来解决问题的一种通用方法.即表明:任何具有演化特征的“自然界”算法都属于或者能够设计成演化算法,任何能够归结为搜索或组合优化问题的问题,都可以尝试用演化算法这一通用的“模型”来解决.
演化算法具有2个基本特征——迭代寻优过程和评估函数,具有这2个特征的自然界算法都可以称为演化算法.迭代是演化计算的寻优手段,在评估函数的指引下,根据既定的算法搜索目标空间,寻找合适的解.这个合适的解可以是最优解,也可以是次优解.演化算法中的评估函数是必不可少的,为了判定某个解的优劣,我们需要评估函数给每个解“打分”,使得任意2个解能够进行比较,选出其中较优的解.我们给出演化算法设计的一般模型:
1) 初始化群体;
2) 寻优过程.
这是演化算法的核心内容,不同的演化算法寻优过程不同,但完成的作用是类似的,即通过不断的迭代,利用评估函数对每个解进行评估,排除评估值较低的解.
评估函数设计:评估函数是演化计算中不可缺少的组成部分,它用于评估当前解的优越性,给出精确的适应值,使得任意2个解能够进行比较.通常我们寻找的目标要满足多个指标要求,因此我们设计的评估函数需要能够同时体现多个指标的能力.评估函数通常定义为
f(x)=α1×β1×x+α2×β2×x+α3×β3×x…,
(1)
其中,x表示个体,α1,α2,α3表示加权系数,β1,β2,β3表示不同的指标.
3) 得到当前最优的解.
2 密码学演化计算的发展过程
传统密码都遵循一种加解密算法固定而密钥随机可变的模式.如果能够使加密过程中加密算法也在不断地变化,则称加密算法是可变的密码,即演化密码.
设E-τ为初始加密算法,演化过程从E-τ开始,最后变为E0.因为E0的安全强度达到了实际使用的要求,所以可以应用于实际.
设S(E)为加密算法E的强度函数,则演化过程可以表示为
E-τ→E-τ+1→E-τ+2→…→E-1→E0,
(2)
S(E-τ) (3) 演化密码的使用能够带来2个好处:1)增强密码强度.由于加密算法在加密过程中因受到密钥控制而不断变化,从而极大提高了密码的强度.若能使加密算法朝着越来越好的方向发展变化,那么这种密码就是一种自发的、渐强的密码;2)提高自动化程度.密码系统的复杂性和困难性是长期困扰人们分析和使用的难题.演化密码的设计理念是基于自然界生物的进化过程,其演化过程中不需要人为操控,符合人们长期追求密码设计自动化的目的.它的出现是人们在密码学领域的研究中迈出的重要一步.2013年武汉大学的张焕国等人证明了攻击演化密码的数据复杂度大于攻击固定算法密码的数据复杂度,从而表明演化密码对抗传统差分攻击的能力高于固定算法密码.体现出演化密码所具有的优势,能够大大提高密码强度[7]. 目前,演化算法已经在密码学的各个领域得到了应用,但关于演化算法何时开始在密码学中使用还没有一个准确的定论,因为数学和密码学有着千丝万缕的联系,就像进化论本身一样,演化计算从单纯解决数学问题,演变到解决密码学问题也是一个渐变的过程.根据收集的参考文献,我们可以大致知道密码学演化计算开始的时间和发展过程,我们将这个发展过程分为4个阶段: 1) 探索阶段(1980~1993) 现实生活中,人们经常需要破译一些简单的替代密码,通常人们根据语法习惯和统计分析的方法来破译.但使用人工统计的方法,既耗费人力、增加成本,且破译时间也不短.为了“偷懒”,人们开始研究如何将这一繁琐的过程自动化.从1980年左右开始,有少数密码学者创新性地使用具有“自动”效果的方法来替代繁琐的人工统计工作[8-10].这一时期并没有演化计算的概念,人们主要采用传统的、简单的人工智能算法实现自动化. 1979年Peleg等人使用松弛算法(relaxation algorithm)通过不断的迭代和更新实现了对替代密码的破译[11],这应该是人工智能在密码学中最早的应用.而后,模拟退火等组合优化算法也被应用到替代密码的研究中[12].这些经典的组合优化算法原理都比较简单,应用也不复杂,但能够达到的破译效果有限,这反映了当时人们在解决密码问题的“智能化”方面还处于一个比较朦胧的阶段. 于此同时,在实际生活应用中,出现了使用人工智能语言(如lisp,prolog,smalltalk等)编写的专家系统,通过分析单个字母或字符串的出现频率,该系统能够破译简单的替代密码[8]. 1993年Spillman等人首次提出利用遗传算法的随机定向搜索特性破译替代密码的新方法[13].这标志着作为演化算法中最早出现和最为经典的遗传算法开始在传统密码的分析中得到应用,也标志着演化计算开始真正进入密码学领域.同年,Mathews的研究表明遗传算法能够有效地搜索巨大的密钥空间,可以作为破译密码系统强有力的分析工具[14].此后有关遗传算法分析替代密码的文献大量涌现,尽管演化计算的概念还没出现,但人们对如何使用演化算法解决密码学问题有了新的提高. 这一时期的研究对象可以分成2类:1)明文破译自动化;2)密钥搜索.分别对应了组合优化问题和搜索问题.研究中,人们发现定义一个评估函数(cost function)是很有必要的,评估函数代表了评判准则,能有效地指引寻优或搜索方向,这样的结构初步具备了演化计算的条件.由于人工智能算法的使用,替代密码等传统经典加密方法已不再具有安全性. 2) 初级阶段(1993~2000) 这一阶段的典型代表是澳大利亚昆士兰大学的Millan教授和他的研究小组——Clark等人,和同一时期的其他研究者不同,他们的研究工作主要集中在Boolean函数设计[15-19]和S盒设计[6]上,统称为演化密码部件设计. 1999年在总结先前工作的基础上,Millan首次在密码学中提出生物演化搜索的概念[6],即模拟生物演化过程或社会性行为建立模型来解决密码学问题.他指出评估函数是演化算法中最重要的组成部分,任何演化计算都需要利用这个评估函数来评估当前解的优越性,给出精确的适应值,使得任意2个解能够进行比较,选出其中较优的解.文献[6]中Millan使用了遗传算法结合爬山法来设计高安全性的S盒.当然,不单单是遗传算法,包括后来出现的蚁群算法、粒子群算法等仿生算法都属于这一演化计算的范畴,它们是解决密码学问题的新的、强有力的工具. Millan小组的研究很有意义,他们为演化密码的研究开辟了一个新的领域,为后续密码学者的研究指引了新的方向.所谓密码部件,就是解决某个数学问题的算法.倘若这个数学问题属于组合优化或搜索范畴,那么该密码部件就可以尝试引入演化算法来提高该密码部件的实现效率. 另外,在密码分析领域,演化算法也有了新的应用.除了常见的替代密码分析外,还出现了对置换密码(transposition cipher)[20]、背包密码(knapsack cipher)[21-24]的演化分析,分析方法还是以遗传算法为主. 3) 成熟阶段多元化(2000~2005) 这一阶段的典型代表是英国约克大学的Clark和他的研究小组成员——Jacob,Stepney等人.作为Millan的后继者,他们在探索密码学演化计算方面所花费的努力功不可没.Clark在2001年发表的博士论文被公认是介绍密码学演化计算的最经典文献[25].他指出启发式搜索算法的能力被极大地低估了,通过使用启发式搜索方法,一定范围的当代密码学问题可以被成功地破译.他们的研究对象主要包括Boolean函数演化设计[26-28]、S盒演化设计[29-30]和安全协议演化设计[31-32].其中,安全协议演化设计是他在2000年提出的一个新的研究方向.在研究方法上,他们开始尝试新的演化算法——蚁群算法,并在置换密码分析中取得成功[33-34]. 除了Clark等人取得的成就外,其他的学者在密码学演化计算的研究中也取得了一些进展,尤其是在密码系统分析(破译)领域.2002年西班牙学者Hernández等人采用遗传算法替代穷举方法搜索合适的掩码,首次成功破译了经过1轮加密的TEA密码(tiny encryption algorithm)[35].2004年Ali等人在对RSA公钥密码分析时,通过结合遗传算法来增强传统时序攻击的能力,并指出增强后的时序攻击同样适用于对DSS和DSA的分析[36],这是演化计算首次出现在公钥密码系统的分析中. 随着密码学演化计算的深入发展,我们国内的一些密码学者也开始接触这一新兴的研究方法.2002年武汉大学的张焕国教授等人首次在国内提出演化密码的概念和密码算法的演化设计方法[37],利用演化算法来加强DES分组密码核心部件——S盒的抗差分性能,并分别以这些S盒组构造DES,得到演化设计的DES密码体制.以这篇文献为指引,他们又利用模拟退火算法和局部爬山法对Bent函数进行演化设计,能够得到几乎所有的6元Bent函数和部分的8元Bent函数.他们的研究工作对国内密码学发展具有十分重要的意义,越来越多的国内学者开始关注演化计算在密码学中的应用. 2004年国家信息安全重点实验室的陈华和冯登国设计了一种包含评估函数、贪婪策略和Hill Climbing的演化遗传算法,利用该算法能够得到高非线性度、低差分一致性的8×8双射S盒,但在扩散性和抗雪崩方面的效果不理想[38]. 2005年陈华等人在Millan爬山法设计的高非线性S盒基础上,研究如何同时改变S盒的3个输出向量的位置来提高S盒的非线性度,提出了MHC算法,在爬山法的基础上进一步提高非线性度[39]. 由于刚刚起步,这一时期国内学者所做的研究工作更多地是学习和参照先前国外的研究成果.研究内容主要集中在Boolean函数设计、S盒设计和DES分析上. 4) 多样化阶段成熟,系统化学说化(2005~现在) 随着密码学演化计算的不断发展,越来越多的密码学者开始接受并认可演化计算,并投身密码学演化计算的研究中,极大地推动了密码学的发展.如印度管理技术研究所的Poonam从2005年开始接触密码学演化计算,他们的研究方向集中在简化的数据加密标准算法(SDES)中,并首次在密码分析中使用文化基因算法[40].还有希腊帕特雷大学的Laskari等人,他们主要研究粒子群演化算法在Feistel等分组密码分析中的应用[41-43].他们的研究表明:密码问题的公式形式或表达样式是决定发挥智能算法性能的关键因素,可以归结为离散组合优化问题的密码学问题才适用于智能算法解决.现有的密码系统很少会泄露任何形式的密文信息或密文内部结构,通常情况下智能算法是分析密文的首选方法. 自2002年首次提出密码学演化计算以来,国内密码学界的许多专家,如张焕国、冯登国、吴文玲、杨义先等研究团队,通过不断的模仿和改进,掌握了许多演化密码设计的方法和技巧,在传统的Boolean函数设计[44]、S盒设计[40]、DES分析[45]上取得了一定的研究成果,同时他们坚持大胆创新,提出了许多新的研究方向和研究方法,如序列密码分析[46-47]、NTRU分析[48]、ECC安全曲线选择等,并在某些方面达到或超过了国外同行的研究水平. 现阶段的密码学演化计算的研究呈现出多样化的发展趋势.在研究方法上,研究者不再单一地使用爬山法、模拟退火和遗传算法,蚁群算法[49-50]、粒子群算法[51-52]、文化基因算法[40]等新兴演化算法也开始得到广泛应用.另外,为了弥补应用某种演化算法带来的缺点,学者们通常会结合使用其他的优化算法,达到优势互补的效果.目前已被提出和应用的混合算法有:混沌模拟退火算法[53]、遗传蚁群算法[54]、量子激励的遗传算法[55]等.在研究对象上,除了传统的研究方向外,研究者开始尝试更多的未知领域,如DES分析、SDES分析、ECC安全曲线构造等. 2011年西北师范大学的马宇红、张杰针对单一演化算法的缺点而提出了一种新的蚁群爬山算法,并将其用于求解连续全局优化问题,其精度和效率优于蚁群算法[56]. 2011年黄冈师范学院的Zhang和Hu设计可以用于遗传算法的适应度函数、交叉和变异策略,然后根据策略设计出产生大素数的算法[57]. 2014年四川师范大学的张凯通过对S盒初始种群的遗传迭代演化,筛选出满足特定密码学性质的S盒,同时分析了通过适应函数与合适的种群规模,交叉变异算子的选择,能够提升遗传算法构建S盒的效率[54]. 2017年深圳大学的王熙照和河北地质大学的贺毅朝[5]对近10余年来利用演化算法(evolu-tionary algorithms, EAs)求解背包问题(knapsack problem, KP)的研究情况进行了较为详细的总结,为今后EAs求解KP提供可行的研究思路. 2018年湖北工业大学徐光辉等人[58]提出一种用于新的信号加密工程应用的混沌系统,该系统成功的实现和制造是通过一个随机数发生器的真实电路来实现的,应用了2种最新的有效优化方法:鲸鱼优化算法(whale optimization algorithm, WOA)和多维优化算法(multi-verse optimizer algorithms, MVO)来优化成本函数. 目前,演化计算已经进入了密码学的各个领域,但不同领域的发展情况各不相同,有些领域的演化设计水平已经十分成熟,而有些领域的演化设计才刚刚开始. 3.1.1 研究背景 布尔函数在密码学、纠错编码和扩频通信等领域有着广泛的应用.密码学中经常需要使用性能较好的布尔函数来设计密码系统,而高非线性和低自相关性是构造较好布尔函数所需要满足的2个基本条件.满足这2个条件的布尔函数能够抵抗线性密码分析和差分密码分析,使密码系统具有较高的安全性.因此,如何构造具有高非线性且低自相关性的布尔函数是密码学家长期关注的问题. 3.1.2 布尔函数演化设计 1997年Millan等人提出利用爬山法(Hill Climbing)修改布尔函数真值表,通过不断优化真值表得到最优的布尔函数.与传统的概率分布式随机产生布尔函数相比,利用爬山法生成的最优布尔函数在平衡性和非线性方面都有了提高. 同年,Millan等人又在以上爬山法的基础上,增加使用了遗传算法,提出利用遗传学算法结合爬山法设计具有贪婪定向搜索功能的算法[15].遗传算法的使用能够快速地产生高非线性度的布尔函数,爬山法的结合同样能够加速这一过程,并且使得产生的布尔函数满足平衡性和相关免疫性的条件. 2002年Clark[25]在Millan的研究基础之上,首次提出利用模拟退火算法(simulated annealing, SA)设计满足多种特性要求的布尔函数,其设计的布尔函数在综合性能方面达到了新的高度. 2011年复旦大学Chunlin等人提出了使用基于遗传算法构造布尔函数的方法,使得到的布尔函数具有良好的加密外观[59]. 2011年Goyal等人[60]采用非支配排序遗传算法II(NSGA-II)结合多目标演化方法设计多指标均衡的平衡布尔函数,实现了4元和5元布尔函数的设计. 2012年印度理工学院的Goyal等人针对保密性强的布尔函数的许多理想特性中找到最佳的平衡这个难题,通过专注于非线性、自相关性和弹性这些特性,找到了一个进化方法来构建拥有最佳权衡4-5个变量的平衡布尔函数[61]. 2013年Clark等人在低差分均匀性的情况下,使用模拟退火、文化基因算法和蚁群优化进行了分组密码中的矢量布尔函数的创建[62]. 2014年印度的Asthana等人提出了一种新的基于遗传算法来产生强布尔函数.该布尔函数拥有满足平衡性、相关免疫性、代数次数和非线性特征的期望值[63]. 2014年荷兰内梅亨大学的Picek等人,针对布尔函数在应用中的一个主要的问题是要找到布尔函数的特定属性,理论上应该找到一个8 b输入和非线性为118的平衡的布尔函数这个现象,专注于研究特定种类的布尔函数,并分析了通过整合代数和进化计算为基础方法寻找期望值,所获得结果的形式应比较靠近理论值[64]. 2015年克罗地亚萨格勒布大学的Picek等人对遗传编程(GP)和笛卡尔遗传编程(CGP)分别在密码分析中进行构建布尔函数进行比较,这也是首次使用笛卡尔遗传编程(CGP)对布尔函数进行构建,结果当目标获得了尽可能高的非线性时,CGP比GP更好[65]. 2016年Picek等人使用演化算法对密码中的布尔函数进行优化[66];同年,克罗地亚的Picek等人使用演化算法设计布尔函数,使布尔函数的非线性度得到了提升,并对不同演化算法设计布尔函数的有效性进行了比较[67]. 3.2.1 研究背景 S盒是大多数分组密码算法中唯一的非线性结构,它的密码强度决定了密码算法的好坏,如何设计出良好的S盒是一个重要的研究问题. 1998年澳大利亚昆士兰科技大学的Millan[68]提出一种通过对换S-盒输出的2个值来提高S -盒的非线性度,实验表明通过随机生成的方式难以获得高非线性度的S-盒. 1999年Millan等人[69]提出基于遗传算法获得高非线性度S-盒的方法.实验表明,该方法获得高非线性度的S-盒比穷举搜索方法更具优势. 2001年美国史蒂文斯理工学院的Jakimoski等人[70]第一次将混沌系统应用到S-盒的构造中,提出混沌映射构造S -盒的方法,证明这些映射构造的S-盒具有可以接受的非线性度和差分均匀度. 2005年重庆大学的Tang等人[71]提出使用混沌映射获得S -盒的方法,详细分析获得的S -盒的双射、非线性度、严格雪崩准则和比特独立准则等密码特性,结果表明所获得的S-盒还可抵抗差分攻击. 2005年英国谢菲尔德大学的Clark等人[72]展示如何寻找一个优秀的单输出布尔函数的成本函数,以便对小型S -盒提供改进. 2005年澳大利亚昆士兰科技大学的Fuller等人[73]综述了构造双射S -盒的启发式方法,证明了通过幂映射可以进化(仅通过迭代变异算子)来生成双射S -盒. 2008年波兰波德拉谢大学的Szaban等人[74]提出了一个基于细胞自动机(cellular automata)生成S -盒的方法,结果表明基于细胞自动机的S -盒有相对于经典S -盒更好的密码属性. 2008年新西兰坎特伯雷大学的Linham等人[75]提出了一个使用启发式方法来构造S -盒的方法,其目标是生成符合严格雪崩准则(SAC),非线性且对差分密码分析具有高度抵抗力的S -盒. 2011年12月哈尔滨工程大学的毕晓君等人针对传统方法设计S盒存在的设计时间过长、易陷入局部最优的缺点,提出了一种基于改变粒子群优化算法的S盒优化设计方法[76],通过改变惯性权重来提高搜索速度和精度来增大算法效率,从而快速地搜索到能有效抵抗差分密码分析和线性密码分析的S盒,改善密码性能. 2012年国防科技大学的李亚鹏等人对遗传算法构造S盒进行优化[77],使得其在密码学性能、收敛速度和适应度值方面有很好的改善.该方法是在初始种群的生成过程中加入由先验知识产生的部分性能较优的S盒,在一定程度上提高收敛效果和收敛速度;采用最优个体保存法选择策略执行遗传算子操作,可以大幅减少额外的计算量;采用Davis顺序交叉法执行交叉操作,引入进化逆转变异法执行变异操作,补偿群体中多样性易损失的不足,同时能够提高算法的搜索效率,加快收敛速度. 2012年8月重庆大学的Wang等人[78]将混沌和遗传算法结合起来构造更高密码性质的S盒的方法,比单纯使用混沌的方法更好地构造更强的S盒. 2013年McLaughlin等人提出了一个确定算法来寻找非线性S盒.“过滤”(filtered)非线性攻击是目前对降低轮蛇(reduced-round Serpent)在达到任意已知明文攻击的最低数据复杂度,并且已经证明了错误密钥随机假设对降低轮蛇的攻击是不完全有效的,降低轮蛇是依赖于现行密码分析或者其变体[79]. 2013年McLaughlin等人利用模拟退火算法找到对于各种S盒的非线性逼近,这些S盒在现有的外轮攻击中可以用于代替线性近似,并提出了11轮蛇的一个新的攻击方法,它比任何已知明文攻击或者选择明文攻击都有更好的数据复杂度,它对于256位密钥有最佳的整体时间复杂度[80]. 2014年突尼斯的斯法克斯大学的Guesmi等人提出了基于混沌函数和遗传算法的新方法来设计强大的替代盒,并分析了S盒的强度,通过对7轮S盒的数值分析表明其较好的S盒近似,并且它们具有较高的抵抗免疫差分分析的能力[81]. 2014年马来西亚国油大学Khan等人设计了一个新的基于混沌的S盒,通过使用DDY(DDT可以有助于对S盒进行差分分析)的系统优化来进行动态设计.该S盒与其他基于混沌的S盒设计相比,有非常低的差分概率,其差分近似概率为8256[82]. 2015年清华大学的覃冠杰等人[83]提出了使用人工蜂群算法来实现随机S -盒的全局优化,实验结果验证该算法的有效性,可以同时优化S-盒的非线性、微分特性和扩散特性. 2015年重庆邮电大学的Wang等人[84]提出了一种结合混沌和优化运算构造具有高非线性度S-盒的新方法.实验结果表明,该方法构造的S-盒比仅基于混沌映射构造的S-盒具有更高的非线性度. 2016年Picek等人[85]基于目前最先进的适应度函数进行实验分析,提出了一个能提供更高速度以及更优结果的新的适应度函数. 2016年Ahmad等人[86]探索了旅行商问题和分段线性混沌映射来合成有效的8×8的S盒,研究结果表明,根据预期设计的S盒将具有更好的保密特性. 2017年日本安全平台实验室的Yu等人[87]在欧密会上提出一种搜索不可能差分的新工具,可以用于检测任何输入和输出差分.同时,该工具也可用于8元S盒性能的检测,也可考虑用于未来S盒的设计优化. 建立在S盒基础之上的DES也同样面临这个问题.目前,对DES类分组密码的主要攻击方法有穷举攻击、差分攻击和线性分析等,而差分分析和线性分析便直接针对DES中的S盒组合密码的迭代结构.因此,演化DES的核心就是演化S盒组,使之符合某种安全准则.S盒的安全准则主要有:非线性准则、雪崩准则和扩散准则[37]. 2017年荷兰代尔夫特理工大学的Picek等人[88]介绍了演化细胞自动机规则的概念,该启发式方法能够为4×4到7×7的尺寸选择最佳的S-盒. 2017年哈尔滨工程大学的Tian等人[89]提出了一个基于交织的逻辑映射(the intertwining logistic map)和细菌觅食优化的混沌S-盒的方法.该S -盒可以有效抵抗多种类型的密码分析攻击. 2017年突尼斯埃尔马纳尔大学的Farah等人[90]提出了一个基于混沌映射和教与学优化(teaching-learning-based optimization)算法获取强S-盒的新方法,实验表明该方法设计的S -盒具有良好的密码学特性,可以抗多种攻击. 2017年巴基斯坦塔克西拉工程技术大学的Khan等人[91]提出了利用差分分布表(difference distribution table)生成混沌S -盒的构造方法.实验表明,该方法获得的S-盒显示出非常低的差分均匀度,同时保持良好的密码特性. 2018年印度国立伊斯兰大学的Ahmad等人[92]提出构建一个基于人工蜂群优化和混沌映射的S-盒的构造方法.该算法旨在优化初始S-盒以满足密码学特性,构造具有高强度的S-盒. 2019年意大利米兰比科卡大学的Mariot等人[93]对基于细胞自动机的S -盒的密码特性进行了系统的研究,证明了该S -盒的非线性度和差分均匀度的上界. 3.2.2 DES的演化设计 1999年Millan指出启发式组合优化算法非常适用于替代盒(S盒)的设计,其设计出的盒具有较高的非线性度和低自相关性[6].他在试验中采用了遗传学算法,通过不断“同化”操作,综合前代不同S盒的优点,产生新一代具有更优性能的S盒,最终收敛到当前最优解. 2004年Clark等人利用模拟退火算法在构造单输出布尔函数上获得了很好的效果[30].事实上,S盒是由若干个布尔输入和输出组成的,因此,S盒的设计可以仿照演化算法在布尔函数中的应用.同年,他将该模拟退火算法推广到S盒的设计中. 2002年武汉大学的张焕国教授等人首次在国内提出演化密码的概念和密码算法的演化设计方法[37],利用演化算法来加强DES分组密码核心部件——S盒的抗差分性能,并分别以这些S盒组构造DES,得到演化设计的DES密码体制. 2012年印度的Jadon等人使用二进制粒子优化算法策略来进行DES对称密钥密码算法进行密码分析.该方法可以确定56 b密钥比特中的42 b密钥比特的位置,BPSO可以用来寻找剩下的14 b密钥比特[94]. 2013年Khan等人提出了一种新的基于蚂蚁密码攻击的群,并将其应用于简单数据加密(DES)的密码分析中,该方法使用已知明文攻击来恢复DES的密钥,并对密钥进行迭代搜索,这些密钥通过蚂蚁在不同运行路线的基础上完成而得到一些候选最佳密钥,然后这些最佳密钥用来寻找DES加密中的56 b密钥中的每个单独的比特.与遗传算法和二进制粒子群算法相比,该方法对DES产生更有效的攻击,且可以减少值的位数[95]. 2012年Rajashekarappa等人提出使用禁忌搜索算法对S-DES进行密码分析的方法.该方法采用了唯密文攻击和基于成本函数值的多种类最佳密钥的产生,从而能够更快的找到S-DES密钥[96]. 2014年Teytaud等人利用启发式算法(meta-heuristics),特别是遗传算法对S-DES进行密码分析,实验表明遗传算法的性能比随机搜索差[97]. 2015年Dworak等人对于S-DES(简化数据加密标准)提出了一种新的密码分析攻击.该攻击是对BPSO(二进制粒子群优化算法)进行修改,它可以在给定的时间周期内对获得结果的质量产生积极的影响[98]. 2017年波兰西里西亚大学的Dworak等人[99]提出了一种针对DES6加密算法的遗传差分密码分析方法,可以将数据加密标准(DES)的新差异攻击减少到6轮.结果表明,该方法可以在85%的情况下破坏K6K6的有效部分. 2018年摩洛哥ChouaibDoukkali大学Grari等人[100]提出了一种新的基于蚁群优化(ACO)的攻击,用于简化数据标准加密(S-DES)的密码分析.实验结果表明,与其他攻击相比,该方法的攻击速度明显加快,并且需要少量已知的明文-密文对,ACO可以作为攻击S-DES中使用的密钥的有力工具. 3.3.1 研究背景 序列密码是密码学的一个重要分支,由于人们对序列密码的研究比较充分,再加上其具有实现容易、效率高等特点,所以序列密码称为许多重要应用领域的主流密码.序列密码的基本原理就是通过明(密)文和移位寄存器产生的密钥序列模2加来完成加(解)密的过程,因此序列密码的关键是产生密钥序列的算法. 3.3.2 序列密码的演化设计 2008年武汉大学的陈连俊等人利用演化算法对滤波模型流密码进行了密码分析.实验表明,该方法具有较小的演化代数和较高的成功率,能够减少密码分析过程中试探密钥的次数,其分析复杂度远远低于穷举攻击的复杂度[46]. 2010年陈连俊等人又对组合模型序列密码中的Geefe发生器和门限发生器进行分析.实验结果表明,演化计算在序列密码相关分析中有重要作用,其中如何设计好适应度函数和选择、杂交、变异等演化算子是演化算法的关键[47]. 2011年Crainicu等人提出一种基于禁忌搜索算法密码分析攻击,该禁忌搜索算法试图重建RC4内部状态[101]. 2014年7月江西理工大学的吴君钦等人针对传统序列密码算法中出现的生成序列密码重码率高和容易陷入局部最优解等缺点,提出了一种基于多目标差分演化的序列密码算法.利用该算法产生的序列密码能够较好地通过各项随机性检验,使用该算法产生了256 b的二进制随机序列.统计分析表明,此序列具有很好的随机性,相比传统演化算法生成的序列,具有更高的随机性和安全性[102]. 2015年波兰的西里西亚大学的Polak等人使用遗传算法对流密码进行分析,来寻找线性移位反馈寄存器近似给定密钥流的最短等效线性系统逼近[103]. 2016年印度理工学院Kumar等人[104]讨论了遗传算法在流密码中的应用.密钥生成是流密码中最重要的因素.这里重复使用遗传算法进行密钥选择.在每次迭代中,选择适应度值最高的键,并与阈值进行比较,所选的键是唯一且不重复的.因此,所选密钥的加密由于密钥的随机性更强而具有高度加密性.结果表明,使用遗传算法生成的密钥是唯一的,对数据加密更加安全. 2018年印度海德拉巴大学Krishna 等人[105]在双目标开发改进和声搜索算法与差分进化算法结合的密钥生成算法.在单目标优化框架中开发第二代非支配排序遗传算法的密钥生成算法,然后对编码的密钥流以及编码的纯文本进行加密,以生成密文. NTRU公钥密码体制是目前后量子密码的研究热点之一.2005年解放军理工大学的赵小龙等人提出利用遗传算法对于NTRU公钥密码体制一种攻击方法[48].因为NTRU的私钥不是唯一的,而是满足一定条件的解集,他们将私钥的样本空间看作一个种群,私钥的每一种取值都看作个体,在定义相应的适应度函数后,搜索密钥就转化为找寻适应度最好的个体. 算法的核心部分包括3个内容:1)编码;2)适应度函数设计;3)遗传算子设计.若公钥和私钥系数中为1的项数已知,那么根据上述3个内容即可用遗传算法搜索私钥的样本空间,寻找适应度最好的样本,其工作流程与经典的遗传算法类似. 2009年解放军理工大学的唐元刚等人[106]利用格理论结合遗传算法对NTRU进行攻击,并对算法的循环交叉操作进行分析,交叉概率取值为0.7~0.9之间时,对搜索结果影响较大.实验表明,遗传算法与一般搜索算法相比,具有一定的有效性和稳定性.NTRU搜索空间随其标准格维数增大呈指数级增长,所以需要构建巨大数量的初始种群,运算量较大. 2016年3月印度的Agrawal和Sharma分别使用蚁群优化算法(ACO)和粒子群优化算法(PSO)对NTRU进行算法的优化.模拟结果显示,与传统NTRU速度相比,使用蚁群优化算法(ACO)和粒子群优化算法(PSO)优化后的NTRU平均速度增加百分比分别为34.65%和41.31%,优化后的NTRU算法速度大大提升[107]. 2016年Agrawal和Sharma在保证较低时间复杂度的情况下,使用遗传算法(GA)、蚁群算法(ACO)和粒子群算法(PSO)对NTRU进行优化.实验结果表明,相对于其他演化算法,使用粒子群算法进行优化时,NTRU的复杂度最高[108],复杂度为O(Nlog(N+1)3)(N为素数),而传统NTRU复杂度为O(NlogN),意味着使用粒子群算法的NTRU提供了更高的安全性. 3.5.1 研究背景 1985年Koblitz和Miller两位密码学家分别独立地提出了椭圆曲线公钥密码体制[1].目前,国际各个标准组织,如ANSI,NIST,SECG等,所公布的安全曲线数量一共不超过30条.由于ECC的研究在中国起步较晚,中国还没有一条属于自己推荐的安全曲线.国内的工程应用绝大多数都是使用美国NIST所推荐的15条曲线.但问题是这些标准组织之间对椭圆曲线的安全定义并不相同,表现在所推荐的曲线数量的不同,如SECG推荐了25条,NIST推荐了15条,而ANSI只推荐了2条.其中只有2条曲线是这3个组织都共同推荐的,其他的曲线有些推荐了,有些没推荐.因此,我们在使用这些曲线时,难免会产生3个疑问:1)如何判定这些曲线是真正意义上的安全?2)这些曲线是否存在某些人为或者非人为的缺陷?3)中国应该怎样选择自己的安全曲线? 3.5.2 ECC安全曲线选择的演化设计 长期以来演化计算在椭圆曲线公钥密码中的应用一直是一个空白.自2004年起,上海大学王潮教授与武汉大学的张焕国教授等人共同提出基于演化计算的安全椭圆曲线快速选择算法[109]. 进一步,王潮教授等人提出了一种基于演化密码和HMM改进的Koblitz安全曲线产生新方法,利用隐Markov模型(HMM)预测迹向量解决基点计算难题,完成了F(22000)以内Koblitz安全曲线的搜索实验,产生的安全曲线基域的覆盖范围、曲线的规模和产生的效率均超过美国NIST的公开报道参数,可提供的安全曲线的基域和基点最高超过1 900 b,远超过美国NIST公布的571 b,在NIST公布的F(2163)~F(2571)范围之间还有新的安全曲线的发现,其所产生的安全曲线与NIST推荐的安全曲线具有相同的安全准则[110-112]. 2016年芬兰图尔库大学的Sahebi等人针对椭圆曲线选择这个难题,提出了一种有效的椭圆曲线选择框架(SEECC),即通过并行遗传算法来选择椭圆曲线中的一条安全有效的曲线,从而提高了椭圆曲线密码体制的安全性和有效性[113]. 2018年印度学者Sujatha等人[114]提出一种改进的椭圆曲线密码体制下的选民身份验证的方法,选民使用私钥,公钥用于对选民进行身份验证.ECC中私钥的选择是通过使用布谷鸟搜索优化技术而不是随机选择值,且该方法使用实时样本数据库进行了增强. 2011年电气与电子技术学院的Omran等人对多字母替换密码使用遗传算法进行密码分析,研究了遗传算法在搜索密钥空间的适应性[115]. 2011年印度内达吉苏巴斯技术学院的Luthra等人探讨了在引入了萤火虫算法的遗传算法中使用的变异算子和一般的交叉算子融合,来对单表替换密码进行密码分析的问题[116]. 2015年印度的Mishra等人使用了爬山算法、模拟退火算法和两者的结合来攻击唯密文攻击模式下的换位密码[117]. 2015年印度尼西亚的Telkom大学的Wulandari等人将差分进化用于解决整数问题置换,用差分进化来攻击换位密码,从而表明了差分进化能够用于正确的解密有高达9的排列长度,但是开始在10个排列长度为10的模拟中有一半不正确答案的密文[118]. 2018年土耳其萨卡里亚大学Demirci等人[119]提出了一种新的基于交换的粒子群优化算法移动算子.该实验测试了操作符的换位密码加密,文本大小为125,250,500和750个字母,密钥长度为5,10,15.在大多数情况下,该算法可恢复70%的密钥. 2011年浙江科技大学的Shen等人使用一种基于双种群遗传算法的改进方法求解0-1背包问题,克服了早熟和在迭代过程中的局部收敛的问题[120]. 2011年北京工业大学的Wei等人提出了一种新的人工蜂群算法解决多维背包问题,介绍了引力的信息素并提出了一种基于吸引力信息素的过渡策略.在算法中,侦查员根据转型策略生成食物来源,并通过与相应的精英食物源进行比较来替换废弃的食物来源,采用蜜蜂和旁观者使用食物来源邻域确定的过渡策略来修改修复算子[121]. 2011年国立卡南大学的Chou等人提出了一种新的量子进化算法,即量子禁忌搜索(QTS),来解决0-1背包问题,其性能优于其他方法(如量子进化算法QEA),没有过早收敛,同时具有更高的效率[122]. 2012年马来西亚多媒体大学的Lee等人提出了优先列表的蚁群算法与突变(PACOM)算法求解多维背包问题,并应用在MKP中[123]. 2012年Taheri等人提出了在Win-Azure’s PaaS环境中使用并行遗传算法(PGA)解决云背包问题,这是首次将遗传算法应用到云背包问题上[124]. 2012年中原工学院的Ling等人提出了使用改进的粒子群算法解决了小规模的背包问题,该算法克服了标准的粒子群算法的缺点,即容易陷入局部最优解且具有收敛精度低.当超过背包的承重时,适应度将为零.当单个粒子的最佳位置与所有粒子的最佳位置相同,则粒子的位置将被重新初始化[125]. 2012年黄河科技学院的 Ma提出结合贪婪变换算法的改进的自适应遗传变换算法来解决0-1背包问题,能够收敛到全局最优解而不至于过早收敛,且具有更快的收敛速度、更高的鲁棒性和更可靠的稳定性[126]. 2013年哈尔滨工业大学的Chen等人提出了使用基于MPI的并行人工鱼群算法求解多维0-1背包问题.该算法能有效地缩短处理时间,且解决了使用基本的人工鱼群算法解决多维0-1问题出现的问题规模变大时数据维数增加,从而难以满足实际要求的难题[127]. 2013年Konggu工程学院的Tharanipriya等人提出了将多聚类遗传算法与粗糙集理论结合的一种改进的混合遗传算法,解决了传统聚类算法局部最优的问题,能够很好地应用于0-1背包问题中[128]. 2013年Jin等人对传统的遗传算法进行了改进,基于遗传和免疫问题提出了一种解决0-1背包问题的新的免疫遗传算法,它可以提高算法的收敛速度,避免遗传算法优化过程中的退化问题[129]. 2013年印度的大学技术研究所的Samanta等人提出了蚂蚁举重算法(AWL)用来解决01背包问题,结果显示了相对于广泛使用的遗传算法来说,该方法在性能和时间复杂度上有显著提高[130]. 2014年泰国Mahanakon科技大学的Anantathanavit等人提出了求解0-1背包问题和多维背包问题的算法.该算法融合了二进制粒子群优化算法(BPSO)和模拟退火以达到目标利益最大,其最大的贡献是通过在局部最优上使用杂交BPSO和模拟退火的方法来摆脱局部最优从而达到全局最优.该方法比单独使用二进制粒子群优化算法或者单独使用模拟退火算法的效果更好[131]. 2014年印度的帕尔大学的Pradhan等人介绍了一种将遗传算法和粗糙理论相结合来求解0-1背包问题的混合算法,遗传算法提供了一种线性时间复杂度为21时解决背包问题的方法,结合了粗糙集理论的属性约简技术,从而减少了搜索空间和保证了有效信息不会丢失,在遗传算法中使用粗糙集理论,提高了遗传算法的搜索效率和质量[132]. 2015年香港大学的Li等人介绍了一种基于变异矩阵的自适应遗传算法,用于求解拥有更高复杂度和结构的一系列的01背包问题,对使用简单背包、平行背包和分层背包3种不同背包问题的数值结果进行了讨论,以及它们的不同效率的启发式解释.从而得到,自适应变异矩阵是最好的,因此,突变的概率是隐时间依赖的[133]. 2015年土耳其耶尔德兹技术大学的Uslu针对背包问题中“包的容量”或者“材料的类型数量”等问题变量增加时,问题规模的复杂度也会显著增加这个问题,采用了遗传算法来求解0-1背包问题[134]. 2015年土耳其的Yasar大学的Tasgetiren等人首次提出了一种可变邻域搜索的差分进化算法来解决多维背包问题.为了提高解的质量,还将使用变邻域搜索的差分进化算法与二进制交换本地搜索算法相结合[135]. 2015年阿尔及利亚的Rezoug等人提出了解决多维背包问题的文化基因算法,首先将遗传算法与一个随机的本地搜索结合(GA-SLS),然后再与模拟退火算法结合[136]. 2017年河北地质大学的贺毅朝等人[137]提出一种基于动态规划的求解随机时变背包问题(randomized time-varying knapsack problem, RTVKP)的精确算法.实验表明,该方法比已有的精确算法更适于求解背包载重较大的RTVKP问题. 2017年2月空军工程大学的薛俊杰等人[138]通过构建一种二进制反向学习方法将烟花算法应用于求解多维背包问题.实验表明,求解多维背包问题中,二进制反向学习烟花算法具有较高的寻优精度、良好的收敛效率和鲁棒性. 2019年印度泰米尔纳德邦VIT大学的Abdel-Basset等人[139]提出了一种改进的鲸鱼优化算法(IWOA),用于解决不同尺度的单维和多维0-1背包问题.实验结果表明,与已有文献的方法相比,IWOA方法在求解0-1背包问题更有效且具鲁棒性. 2019年土耳其Dokuz Eylül大学的Ozsoydan等人[140]提出了一种基于遗传算法和粒子群优化的简单而有效的二元群智能技术.实验研究表明,该方法与已有文献的结果相比,得到显著的改进,且该方法可方便地应用于其他元启发式算法中,提高算法的效率. 2013年印度得利科技大学的Jhajharia等人针对公钥密码系统伪随机数生成器(PRNG)广泛应用于生成特定的密钥和人工神经网络(ANN)中的随机数,且ANN已发现有很多种可能的攻击问题,提出了使用遗传算法的人工神经网络(ANN)的公钥密码系统密钥产生方法.该方法克服了ANN传统PRNG生成随机数的缺点,对于生成的公钥和私钥,要使用不同数量的混合轮,保证私钥的生成不会由公钥得到[141]. 2011年西班牙的Cárdenas-Montes等人介绍了4种进化算法在性能上对随机数生成器的变化所产生的影响:粒子群优化、差分进化、遗传算法和萤火虫算法[142]. 2017年捷克学者Chlumecky等人[143]提出一种利用遗传算法(GA)对降雨径流模型进行优化的新方法.遗传算法使用进化原理结合随机数生成器估计模型参数.实验结果表明,该方法在模型的输出质量上呈现出稳定的趋势.与以往的研究相比,该方法加速了模型的标定,并对降雨径流模型进行了改进. 2019年赫瑞-瓦特大学Zanforlin等人[144]提出了一种基于2个独立连续波激光源间采样相位随机化的光学量子随机数生成器(QRNG)算法.详细分析了基于QRNG的外差测量方法,以Kullback-Leibler散度为基准,量化了设置偏差的影响,以评估安全随机数生成的限制条件. 量子环境下的密码理论研究目前主要包含3类,且都是国外学者提出的:1)Shor算法等通用量子算法对公钥密码的攻击;2)抗量子密码研究,比如基于NP问题的格密码研究;3)量子密码研究. 上海大学王潮教授等人独立提出第4类研究:(基于量子人工智能的)量子计算机密码设计.之前,国际上暂未发现通用及专用2类量子计算机用于密码设计领域的公开研究及报道. 在2012年王潮教授等人[145]提出D-Wave量子计算机设计密码的潜力和可行性,以对称密码体制中的关键密码部件布尔函数为研究对象,于2017年率先在国际上首次完成基于真实D -Wave 2000Q系统的抗多种密码攻击的密码函数设计实验[146]. 通过深入分析对称密码体制关键部件布尔函数在理论设计和搜索优化方面实现多指标均衡所面临的瓶颈,提出布尔函数三大安全指标(非线性度、相关免疫、平衡性)的量子自旋模型及可保证实际量子退火精度的安全指标映射量子Chimera图的可扩展方案,成功完成小规模Bent函数设计和具有高非线性度的4元弹性函数设计. 王潮教授等人将量子计算设计密码的研究视为一个新的量子研究领域,命名为量子人工智能密码量子计算密码,旨在利用D -Wave量子计算机量子隧穿原理量子退火这一量子人工智能算法,结合密码函数背景,将密码设计问题映射为D -Wave量子退火擅长处理的组合优化问题,借助量子退火相比传统计算的指数级空间搜索优势处理,是一种不同于传统密码搜索分析和理论设计的密码设计思路和方案 该研究获得了国内外著名学者的肯定评价,例如国际著名的量子物理专家、《Nature》资深评论员、ETH Zürich的Troyer教授于2015年12月对这一探索性实验工作给予积极肯定:“It is important to look for new applications”.2016年7月,王育民教授评价:“如何借助加拿大的D -Wave计算机,巧妙发挥量子的一些物理特性,有效地解决密码设计中的计算困难问题是你们工作的意义所在.” 业内长期以来认为Shor算法是唯一有效的攻击RSA的量子计算算法,在抗量子密码的研究方面几乎仅考虑到Shor算法的潜在威胁.实际上根据《Nature》和《Science》报道,均认为实现Shor算法破译仍旧遥遥无期[147-149].Google首席量子计算机科学家、原加州圣巴巴拉分校的Martinis教授及国际量子专家、Microsoft量子研究组首席研究员Troyer(原苏黎世理工联邦理工学院教授)均表示通用量子计算机的实用化,包括采用Shor算法破译实际RSA公钥密码等典型应用,遥遥无期[147-149]. 通用量子计算机的进展缓慢,对实际运行的公钥密码不能构成安全威胁,需要寻找Shor算法之外的量子算法攻击公钥密码.业内认为基于量子退火的专用量子计算机D -Wave对信息科学非常重要:有利于解决“有指数级可能性的答案”搜索,这也是考虑将D -Wave量子计算机用于密码设计及密码分析的基础. 上海大学王潮教授等人基于D-Wave原理量子退火,提出了可用于小量子比特实现整数分解以攻击RSA公钥密码的通用量子计算模型.基于D -Wave量子计算软件环境,有效实现20 b整数的分解[150],获得了目前量子计算破译RSA公钥密码的最大指标,而2019年1月8日最新推出的IBM Q System OneTM运行Shor算法在理论上最大只能分解5~10 bit整数,也超过了洛克希德马丁公司研究员采用量子退火破译RSA的最大规模7781[151]. 该研究于国内首次验证了D -Wave破译RSA的潜力,这是不同于Shor算法的第2种攻击方法,也说明该方法比Shor算法更具现实攻击力.要获得同样的攻击效果,Shor算法至少需要40多个量子比特,所需精度及规模都远非目前通用量子计算机所能达到.目前最大规模的谷歌72量子比特Bristlecone(“狐尾松”)芯片,还不是精确的量子比特,由于量子纠错问题(surface code码)等技术瓶颈无法形成密码破译能力,外部环境的微小干扰都可能导致计算错误. 王新梅教授在《Science China Physics,Mechanics & Astronomy》对文献[150]研究撰写的Highlight[152]中指出:“如能用量子退火算法攻击其他知名密码算法也是有意义的”.更进一步,不仅需要重视D-Wave对RSA及其他公钥密码体制的攻击可行性,未来抗量子密码研究也需要重视来自D -Wave专用型量子计算机的攻击可行性.《Science》出版机构——美国科学促进会(American Association for the Advancement of Science——AAAS)在EurekAlert上对该研究成果进行报道,截止2019年7月底点击率为13 399次.同时,科学网、IEEE对该研究也进行了相关报道. 2018年11月ETSI会议的一些标准组织专家认为,也正是因为D -Wave最初的应用是洛克希德马丁公司战机飞控软件测试、谷歌图像识别等,与密码学领域无关,当前对D-Wave在密码学领域方面的应用遭到忽视. Grover算法与侧信道攻击的结合,可以拓展Grover算法的攻击有效性. 2016年贾徽徽等人[155]将Grover量子搜索算法和中间相遇攻击相结合,提出了一种新的搜索算法—Grover量子中间相遇搜索算法,并将其应用于纠正ECC侧信道攻击中出现的错误密钥位.与传统搜索算法相比,计算复杂度大幅降低.实验结果表明,该方法能够以成功率1纠正ECC攻击中出现的错误位. 2017年王潮教授等人[156]提出基于0.1π旋转相位Grover算法的椭圆曲线密码电压毛刺攻击算法.实验结果表明,该方法能以100%的概率攻击NIST发布的Kob1itz安全曲线K-163,计算复杂度呈指数级下降.该方法是除Shor算法之外量子计算对公钥密码的一种新的有效的量子密钥攻击方法. 我们对演化密码学与量子人工智能密码的发展现状有了初步分析.目前,我们收集了该领域自20世纪80年代以来的100多篇文献,这些文献几乎涵盖了当前密码学演化计算的所有内容,通过分析,我们希望能够为国内人工智能与密码学结合的研究提供参考. 演化密码学的研究方法就是指研究时所采用的演化算法.根据“演化”的定义,我们将演化算法分成2类——基于自然进化原理的算法和模拟生物社会性行为的算法.图2展示了国内外在密码学研究中已经得到应用的演化算法. Fig. 2 Evolutionary Algorithm classifications in cryptography图2 密码学演化算法分类 根据演化计算应用的情况,我们将密码学问题分为:密码分析(破译)、密码部件演化设计.其中,人们对密码分析(破译)的研究由来已久,它也是研究者关注最多的领域,其次是密码部件设计. 在密码分析(破译)中,以替代密码为代表的传统密码体系已经被成功破译,现在的研究热点主要集中在对DES,SDES分析中,对公钥密码RSA,ECC的分析也是未来的研究方向.在密码部件设计领域,演化计算在Boolean函数设计和S盒设计中的应用已经十分成熟,但此后创新性的研究很少出现.基于启发式搜索的密码安全协议设计最早由Clark提出,由于限制条件很多,目前该方向的研究者并不多.图3显示了当前密码学演化计算的主要研究方向. 这里我们只列出具有代表性的研究人物和他的团队,包括Millan研究团队、Clark研究团队、Laskari研究团队和国内的张焕国研究团队.图4展现了各个研究团队的主要成员以及他们之间的联系,图4中连线表明两者曾一起发表过论文. Fig. 4 Popular research team of evolutionary cryptography图4 演化密码学的主要研究团队 演化密码学涵盖了密码学和演化计算2个学科内容,但人们更愿意将其作为人工智能应用的成功案例.当前,绝大多数密码学演化计算相关文献来源于各种智能计算、信息安全和演化计算的相关国际会议和期刊.而密码学会议或期刊却很少收录有关演化计算的论文,代表密码学最高级水平的三大会议——美密会、欧密会和亚密会——近10年来很少收录有关密码学演化计算的文章,最早的一篇还要追溯到1998年Millan在欧密会上发表的关于的Boolean函数启发式设计的论文[18].演化密码的发展任重而道远.我们从收集的100多篇相关文献中选出107篇,按照主要的出版机构分类作了统计和总结,如表1所示: Table 1 Classifications of Relevant References on Evolutionary Computation in Cryptography表1 密码学演化计算相关文献分类 Note: The numbers in brackets represent the number of papers published in the corresponding journals. The full name of Journal: ICCIMA—International Conference on Computational Intelligence and Multimedia Applications;S&P—Security and Privacy;CEC—Congress on Evolutionary Computation;ICHIT—International Conference on Hybrid Information Technology;ICEEC—International Conference on Electrical Electronic and Computer Engineering;ICCIS—International Conference on Computational Intelligence and Security;ICISA—International Conference on Information Science and Applications;ISA—Intelligence Systems and Applications;WiCom—Wireless Communications;GECCO—The Genetic and Evolutionary Computation Conference;IJCSNS—International Journal of Computer Science and Network Security;IJCSIS—International Journal of Computer Science and Information Security. 从出版机构来看,将近一半的演化密码学相关论文被收录在IEEE和Springer中,另有一半零散地分散在各个大学的电子数据库和其他的一些出版机构.从论文来源角度来看,早期的演化密码学论文主要出现在介绍性的Workshop和某些学者的博士论文中,而后开始出现在一些较知名的人工智能计算相关的国际会议上,固定期刊收录的很少. CEC是当前演化计算领域最大和最具影响力的国际会议,演化密码学相关的论文主要发表在CEC中,并大都被IEEE下属的Evolutionary Computing期刊收录.受IEEE Computational Intelligence Society和Evolutionary Progamming Society资助,CEC从1999年开始每年举行一次,会议内容包括进化机器人、多目标优化、进化硬件、进化计算理论等人工智能计算及应用的多个研究领域,演化密码学作为人工智能演化计算应用的成功案例也属于该会议的讨论范畴.与之齐名的GECCO和PPSN也都是人工智能领域较有影响力的国际会议,但它们很少收录密码学相关的论文. 演化密码已经发展了20多年,得到了国家自然科学基金面上项目和重点项目等连续支持,并已经历了20多年的历程,在对称密码和非对称密码均取得了丰硕的研究成果.在演化密码安全性分析、演化DES密码体制、演化DES密码芯片、密码部件(如S盒、P置换、轮函数和安全椭圆曲线等)的设计自动化、Bent函数等密码函数的分析与演化设计、密码的演化分析、协议演化设计等方面获得实际成功.表2中,我们简单汇总了当前演化密码学的研究成果. Table 2 Summary of Popular Research on Evolutionary Cryptography表2 演化密码学研究现状汇总 Note: √ represents the study of corresponding algorithms in this field. 今后的演化密码发展可能有3个方面: 1) 针对目前已有的密码部件设计方法,演化密码方法不是否定传统的密码分析设计方法,有望成为已有的密码部件设计方法的一种增强手段.在需要对密码部件设计某一过程参数进行穷举搜索的情况下,更快地搜索出好的参数;或是在已有较好的密码部件设计参数情况下,可以进行局部寻优,有较大的概率对现有的参数进行进一步优化. 2) 演化计算可以增强已有的密码分析方法自动化,对传统方法进行增强,成为密码分析的有力手段.对于现代高强度密码,如果安全强度达到指数级或者亚指数级,单纯依靠演化算法或许搜索量依然很大.但是演化算法的使用可以降低密钥搜索空间的数量级,使已有攻击方法如虎添翼,在这些攻击方法的已有攻击能力基础上进一步减少搜索空间量级. 3) 发展量子人工智能密码.通用量子计算机进展缓慢,而加拿大D-Wave商用量子计算机发展迅猛,已与Martin,Google,NASA、美国国家实验室等众多机构合作,完成100多个先期应用,有望成为量子计算商用化的突破点.D-Wave量子计算机在密码学领域的研究鲜有人关注,目前国际上暂未发现通用及专用2类量子计算机直接用于密码设计领域的公开文献报道. 演化密码思想已经具备人工智能密码的主要特征,本文进一步拓展到量子人工智能密码,在国际上首次由中国学者提出了量子计算机密码设计的原创性理论,并于2017年底在国际上首次完成真实D-Wave 2000Q量子计算机密码设计实验.国际量子专家Troyer教授指出了量子人工智能密码框架应用探索的重要性. 在密码破译领域,在国内首次提出了提出一种完全不同于著名的Shor算法的量子攻击方法,验证了D-Wave分解大数破译RSA密码的潜力,成功实现20 bit整数的分解.获得了目前量子计算破译RSA公钥密码的最大指标,对2019年1月8日最新推出的IBM Q System OneTM运行Shor算法破译RSA的理论最大值形成超越. Grover量子搜索算法在椭圆曲线侧信道攻击中的应用,大大降低攻击的计算复杂度,提高算法的搜索效率,同时也拓展了Grover算法的攻击能力. 4) 演化密码有望对一些新型的密码体制分析和设计提供探索性研究,并发展到人工智能智能密码. 演化密码可以加速NTRU的并行攻击效率,融合人工智能方法,有望应用于后量子时代的密码算法设计和分析. 演化密码是演化算法和密码学的理论应用发展的历史必然,是密码智能化发展过程中的一种成功实践.演化密码已经具备了智能密码的一些特征,演化密码是进一步发展为智能密码的有效途径. 就密码安全性理论而言,演化密码思想融合人工智能方法,有望快速产生一批可以实用的亚优解,达到一次一密码算法的作用,类似跳频通信,增强密码系统安全性. 全体作者感谢刘礼黎、贾徽徽,曹琳在他们硕士研究生学习阶段对本文做出的贡献.3 国内外研究现状
3.1 Boolean函数设计
3.2 S盒设计与DES设计
3.3 序列密码设计
3.4 NTRU破译
3.5 ECC安全曲线选择
3.6 换位密码(transposition cipher)、替换密码
3.7 背包问题分析
3.8 随机数的产生
4 量子人工智能密码设计与分析
4.1 量子人工智能密码设计
4.2 基于量子退火的整数分解
4.3 Grover 量子搜索算法在ECC中的应用
5 演化密码学与量子人工智能密码的总结
5.1 演化密码学的研究方法
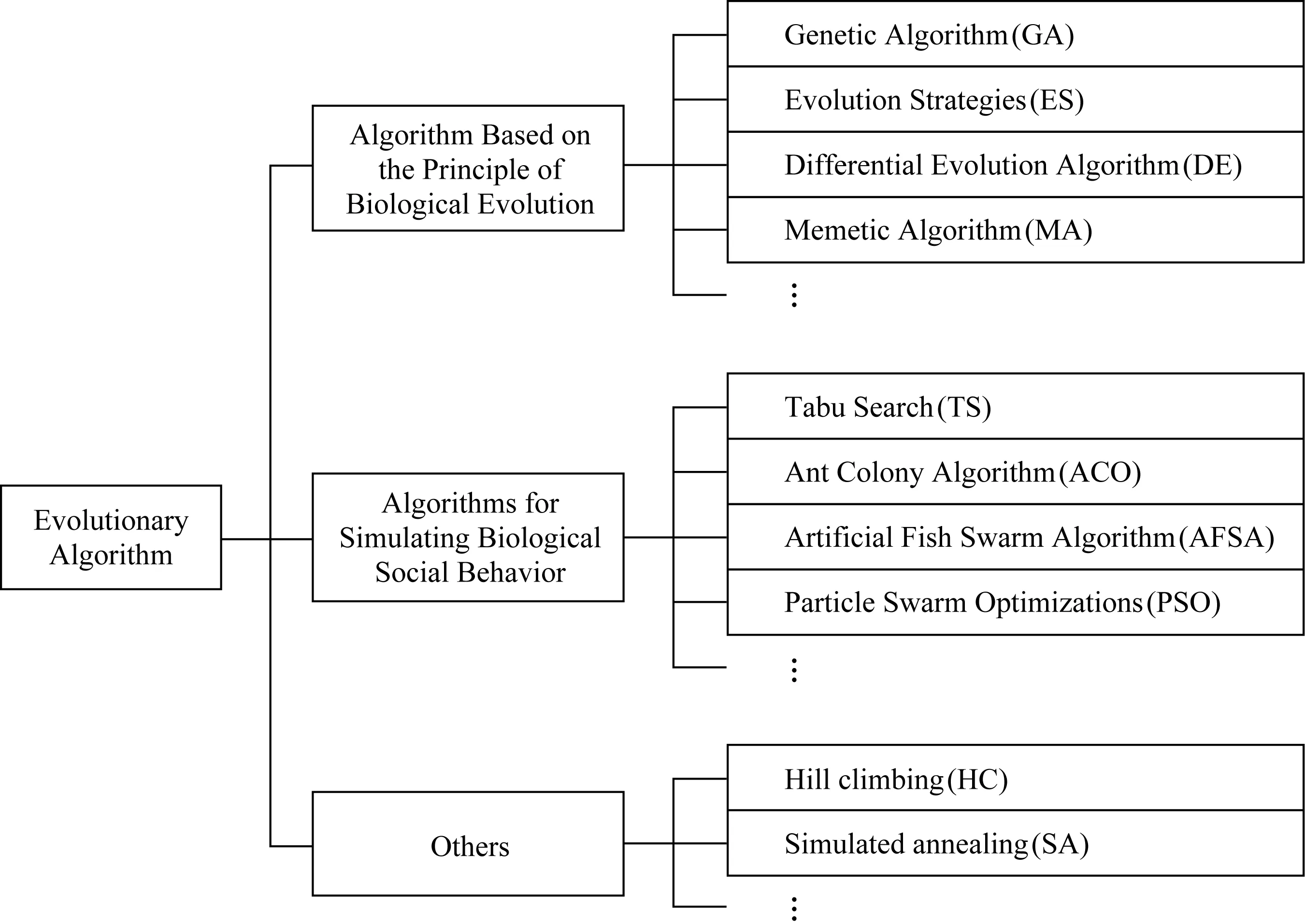
5.2 研究方向
5.3 研究团队
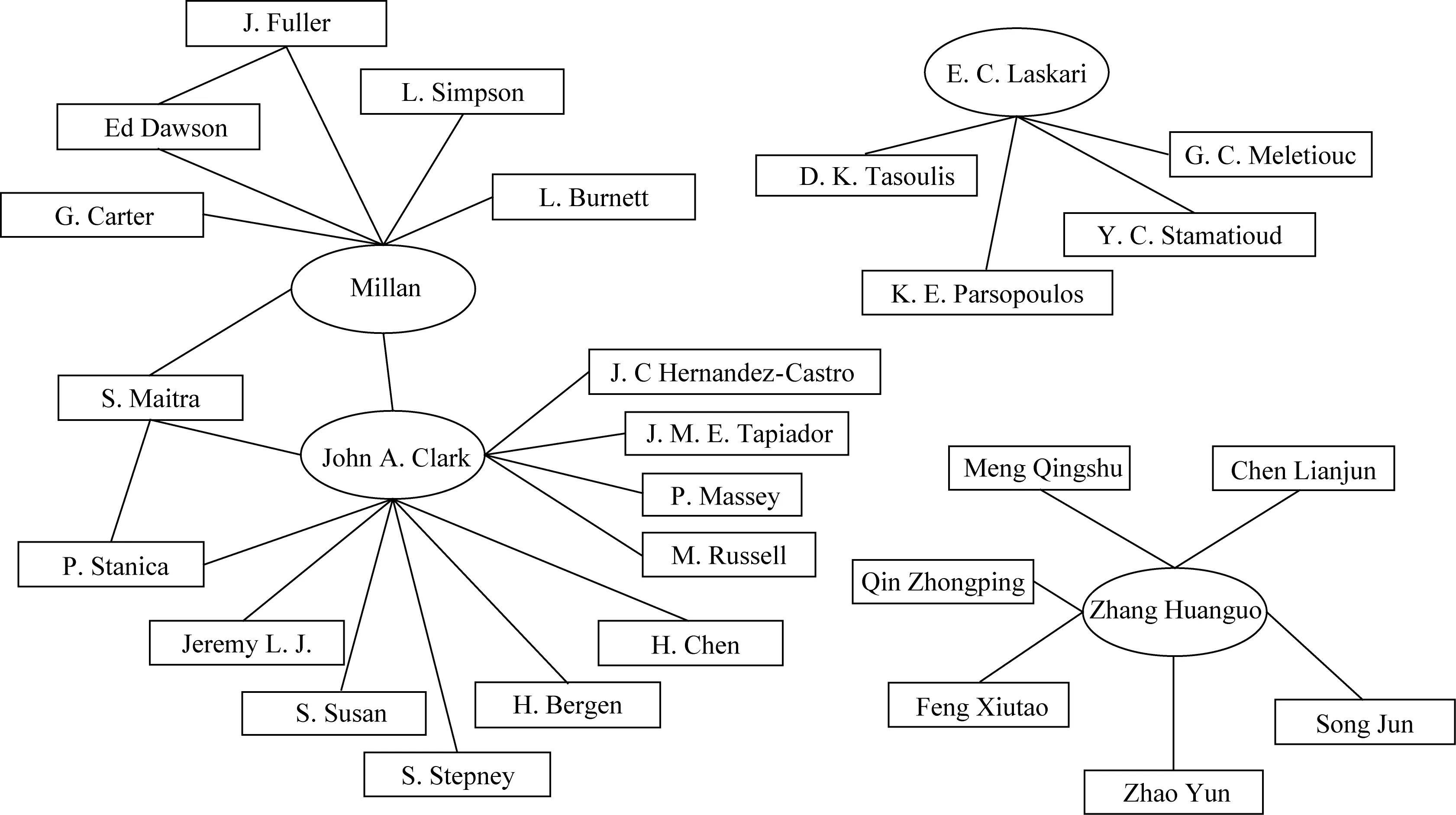
5.4 相关会议和期刊

6 演化密码到量子人工智能密码的展望