树突神经网络分析
2019-10-20刘向文李玮葛瑞泉
刘向文 李玮 葛瑞泉

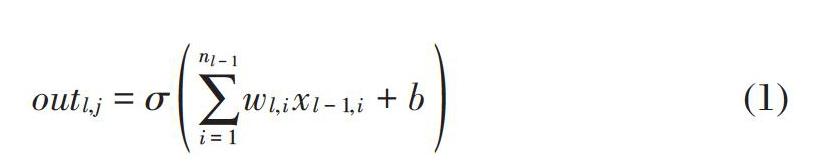

摘 要: 树突神经网络(DENN)是一种含有局部非线性树突结构的特殊神经网络模型。文章研究了DENNs在网络结构变化的情况下模型的学习行为。在有监督学习任务的实验中发现,局部非线性结构的DENNs可以提高模型的表达能力,并且在中等树突分支数量时表达能力最强,在网络较小的情况下DENNs模型比常规前馈型神经网络的优势表现得更加明显。在随机噪声数据集上的实验中发现DENNs拟合能力的优势不明显,这种现象进一步表明,DENNs的容量优势与自然图像数据中的冗余有关。
关键词: 树突神经网络; 局部非线性; 有监督学习; 网络表达能力
中图分类号:TP391 文献标志码:A 文章编号:1006-8228(2019)09-08-05
Analysis on dendritic neural network
Liu Xiangwen, Li Wei, Ge Ruiquan
(School of Computer Science and Technology, Hangzhou Dianzi University, Hangzhou, Zhejiang 310018, China)
Abstract: Dendritic Neural Network (DENN) is a special kind of network with localized nonlinearity. This work studies the learning behavior of DENNs when the network architecture is altered on various aspects. In the experiments of supervised machine learning task, it is found that the locality structure of DENNs can improve the expressive ability, and the expressive ability is strongest when DENNs with mid-size dendrite branch numbers, and DENNs show even greater advantage over the standard feedforward neural networks when network sizes are small. It is found that the fitting ability of DENNs is not obvious in the experiment on noise data learning task, this phenomenon further indicates that the improved model expressivity of DENNs owe to the structural redundancy of natural image data.
Key words: dendritic neural network; local nonlinearity; supervised learning; network expressive power
0 引言
近年来,深度学习算法在很多领域取得了显著进展。人工神经网络最初以感知机[1]形式构建,其单元通常被构建为突触输入的加权和,通过激活函数得到输出。几乎所有现代人工神经网络都使用了这种模型。然而,生理学领域的实验和建模发现,生物神经元比上述模型更为复杂。研究表明,树突结构中包含大量活跃的离子通道[2-3],突触输入可能对其邻近的突触输入产生非线性影响。此外,强有力的证据表明生物学可塑性机制也在树突内起到局部作用[4]。这些特性极大地促进了局部非线性成分在神经元输出中的作用,并赋予神经网络更高的信息处理能力[5-7]。文献[8]对树突的局部非线性和可塑性进行了建模,将活跃的树突结构应用到传统的人工神经网络中,构建了树突神经网络(Dendritic Neural Network,DENN)模型,本文在文献[8]的基础上进一步探索组内稀疏的树突结构网络模型在学习过程中的表现。实验表明DENN与标准前馈神经网络(Feedforward Neural Network, FNN)相比有较高的网络复杂性,具体表现为在图像数据集和随机标签图像数据集上的拟合能力比標准FNN明显,在高斯噪声数据集上的优势相对不明显。
1 树突神经网络
在生物神经网络信息传递和处理过程中,树突有很强的非线性交互作用,如图1是神经元之间信号传递示意图。树突将上游神经元接收过来的突触输入传递给神经元,经处理后,通过轴突把动作电位信号传递给下游邻近的神经元。
DENN模型构建了含有这种树突结构的人工神经网络,其模型结构如图2(b)所示,与图2(a)标准的、全连接的FNN模型相似,模型中的每个神经元也接收来自上层的输出数据,并且模型的最后一层与标准FNN相同。模型把标准FNN的隐藏层分解为两个阶段。在第一阶段,树突分支获得与输入稀疏连接的线性加权;在第二阶段,所有分支的输出被非线性地整合输出。模型确保每个模式学习事件被隔离在树突分支内部。
● 树突神经网络定义
在标准FNN模型中每一个隐藏单元接收其前一层中所有单元的激活信息作为输入,计算加权和,通过激活函数处理后形成本单元的输出,表示形式如下:
[outl,j=σi=1nl-1wl,ixl-1,i+b] (1)
其中,[l]表示网络中第[l]层,[x]为输入,[w]为权重向量,[b]为偏执向量,[σ]为激活函数。本文激活函数主要考虑用整流线性单元(ReLU)即[σ=max0,outl,j]。
和标准FNN模型相比,DENN由多个树突层组成,第[l]层具有[nl]个树突单元,并且每个树突单元和一个神经元输出相关联,每个神经元的输出是[d]个树突分支激活信息的最大值。每个树突分支和上一层的[k]个输入单元连接。为避免冗余拷贝,连接策略设计为每个分支从[nl-1]个输入单元中随机无重复选择[k=nl-1/d]个输入单元连接,其中[k≤nl-1],[k]被称作分支大小,[d]被称作分支数量。
在树突层中每个树突分支可以表示为如下形式:
[zl,i,j=t=1nl-1(Sl,i,j,t?wl,i,j,t)xl-1,t,i∈[nl],j∈[d]] (2)
其中,[xl-1]為输入,[w]为权重向量,[Sl]是0,1矩阵,代表树突分支和输入之间是否有连接,0代表没有连接,1代表有连接。利用预先分配的随机种子生成[Sl],使用适当的算法,[Sl]不会产生额外的存储和传输。
每个神经元的输出是[d]个分支的最大值,表示为如下形式:
[outDl,i=max(zl,i,j)+b,i∈[nl],j∈[d]] (3)
其中,[b]为偏执向量,当[d=1]时,树突层与具有线性激活功能的全连接层相同。DENN模型的输出层[out]与标准FNN模型的输出层相同。
2 实验结果与分析
2.1 图像数据集结果分析
实验选用有标签的Fashion-MNIST[9],CIFAR-10和CIFAR100[10]图像数据集。Fashion-MNIST数据集中有60,000个训练样本和10,000个测试样本,每个样本是28×28像素的灰度图像。CIFAR-10/100数据集由50,000个训练图像和10,000个测试图像组成,每个图像是32×32的彩色图像。
我们在实验中构建了DENN,加入Batch Normalization[11]的标准FNN(BN-ReLU)和加入Layer Normalization[12]的标准FNN(LN-ReLU)三种网络模型。所有对比实验的网络模型都由三层组成,前两层中每层有[n]个单元,最后一层有10/100类输出。使用ReLU函数处理所有隐藏单元的输出,使用Softmax函数生成网络输出。实验中所有网络模型的参数数量不变。对于DENN,实验中每个神经元中树突分支为[d]时,输入权重的数量被设置为[nd],以保持输入的数量与标准FNN隐藏层中的数量相同。DENN的输出层与标准FNNs一样。
使用Adam优化方法[13]训练所有模型100个周期,学习率从1e-2指数衰减至1e-5。为了能更好的观察在不同的网络容量下模型学习行为的变化,隐藏层单元大小分别设置为64,128,256和512。在训练模型前数据集中的样本均做标准化预处理,训练过程中不使用任何正则化方法。
图3显示出了网络模型的分支数量和隐藏单元数变化时在图像数据集上模型训练准确率和训练损失结果。图3(a1),3(b1),3(c1)[8]分别为在Fashion-MNIST,CIFAR-10和CIFAR-100数据集上的训练准确率;图3(a2),3(b2),3(c2)[8]分别为在Fashion-MNIST,CIFAR-10和CIFAR-100数据集上的训练损失。从图3中可以看出DENNs可以获得比FNNs更好的网络拟合能力,网络模型的拟合能力随着分支数量的增加首先呈现增加的趋势,然后下降。树突分支在中等数量的情况下,拟合能力最强,可获得比标准FNNs低很多的损失,DENNs在极端树突分支数量的情况下(比如2,128),造成的损失比中等分支高。
2.2 随机标签图像数据集实验结果分析
实验选用随机标签的CIFAR-10/100图像数据。具体描述参见上节的图像数据集,和图像数据集不同的是样本对应的标签是随机打乱的,实验中网络模型参数设置和图像数据集相同。
图4显示出了网络模型的分支数量和隐藏单元数变化时在随机标签的图像数据集上模型训练准确率和训练损失结果。图4(a1),4(b1)分别表示在随机标签CIFAR-10,CIFAR-100数据集上训练的准确率;图4(a2),图4(b2)分别表示在随机标签CIFAR-10,CIFAR-100数据集上的训练损失。在这样的数据集上,网络模型不能利用数据中的通用特征,因此需要更大的模型容量[14]。通过实验结果对比可以看出,网络能够拟合随机标签的数据,当网络单元足够多时可以获得接近零的训练误差。模型在限制网络容量压力情况下,DENNs模型拟合能力明显优于标准FNNs,尤其是在隐藏单元较小的情况下效果较为明显。
从图4(a1)和图4(b1)的比较结果中可以看出:当网络隐藏层单元数量达到一定数量(比如512)时,模型在两个数据集上的比较结果没有明显差距。由于网络拟合CIFAR-100数据集比CIFAR-10数据集需要更大的模型容量,所以较小的隐藏层单元数量的模型在CIFAR-10数据集上的拟合效果比在CIFAR-100上的拟合效果好;由于网络模型在随机标签的数据集上不能够利用相同标签数据的共同模式,所以在图3(b1)与图4(a1),图3(c1)与图4(b1)中网络模型在图像数据上的拟合效果比在随机标签数据上的拟合效果好。
2.3 高斯噪声数据集实验结果分析
数据集使用60,000条随机产生均值为0方差为1的高斯噪声数据,每条数据包含784维度信息,以便进一步评估DENNs的拟合能力,实验中网络模型的参数设置和图像数据集相同。
图4(c1),图4(c2)显示出了在高斯噪声数据集上网络模型的分支数量和隐藏单元数变化时的训练结果。图4(c1)表示训练的准确率,图4(c2)表示训练损失。本数据集消除了数据冗余,网络模型需要更大的记忆能力拟合整个数据集。实验结果可以看出,网络模型能够拟合随机高斯噪声数据。相对于随机标签的数据集模型更容易达到接近零的训练误差。通过比较可以看出,DENNs拟合能力随着分支数量的增加先上升后下降,拟合能力仍然在中等分支数量情况下最好。同图像数据集上实验结果相比,DENNs比标准FNNs在高斯噪声数据集上的拟合能力优势不明显,这表明 DENNs模型在学习中更能利用数据内部的相关性。同随机标签图像数据集上的实验结果相比,DENNs比标准FNNs在高斯噪声数据上的拟合能力优势不明显,其中的原因可能是,随机像素的输入比自然图像更加离散,网络模型更加容易拟合相对离散的噪声数据。
3 结束语
本文在DENN神经网络模型的基礎上,进一步研究了模型在改变分支数量和网络结构的情况下学习行为的变化。实验表明,DENN能利用数据中的通用特征提高模型的拟合能力,在更大网络容量压力下,DENN在图像数据集和随机标签图像数据集上表现出比标准FNN模型更好的拟合能力。DENN在高斯噪声数据集上相比标准FNN并没有表现出明显的优势。未来的研究,可以继续探索DENN学习行为变化的内在原因,同时可以将树突结构和卷积网络相结合,应用于计算机视觉领域,进行特征提取提高模型的拟合和泛化性能。
参考文献(References):
[1] Rosenblatt F. The perceptron: A probabilistic model for information storage and organization in the brain [J]. Psychological Review,1958.65(6):386-408
[2] Mel B W.Synaptic integration in an excitable dendritic tree[J].Journal of Neurophysiology,1993.70(3):1086-101
[3] Greg Stuart,Nelson Spruston, and Michael H?usser. Dendrites[M].Oxford:Oxford University Press,2016.603-639
[4] Losonczy A,Makara J K, Magee J C. Compartmentalized dendritic plasticity and input feature storage in neurons[J]. Nature,2008.452(7186):436-41
[5] Poirazi P,Mel B W.Impact of Active Dendrites and Structural Plasticity on the Memory Capacity of Neural Tissue [J]. Neuron,2001.29(3):779-796
[6] Wu X E, Mel B W. Capacity-Enhancing Synaptic Learning Rules in a Medial Temporal Lobe Online Learning Model [J].Neuron, 2009.62(1):31-41
[7] Poirazi P,Brannon T, Mel B W.Pyramidal Neuron as Two-Layer Neural Network[J].Neuron,2003.37(6):989-999
[8] Wu X,Liu X.Improved Expressivity Through Dendritic Neural Networks[C]//Advances in Neural Information Processing Systems. 2018:8067-8078
[9] Xiao H, Rasul K, Vollgraf R. Fashion-mnist: a novel image dataset for benchmarking machine learning algorithms[J]. arXiv preprint arXiv:1708.07747, 2017:1-9
[10] Krizhevsky A,Hinton G.Learning multiple layers of features from tiny images[R]. Technical report, University of Toronto,2009:9-53
[11] Ioffe S,Szegedy C.Batch normalization:Accelerating deep network training by reducing internal covariate shift[J]. 2015, arXiv preprint arXiv:1502.03167:1-11
[12] Ba J L,Kiros J R,Hinton G E. Layer normalization[J]. arXiv preprint arXiv:1607.06450,2016:1-14
[13] Zhang C,Bengio S, Hardt M,et al.Understanding deep learning requires rethinking generalization[J].arXiv preprint arXiv:1611.03530, 2016:1-15
[14] Kingma D P,Ba J.Adam:A method for stochastic optimization[J].arXiv preprint arXiv:1412.6980,2014:1-15
