参数较小的最优局部修复码的构造

蒋静 李勇刚

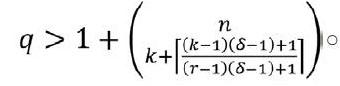
摘   要：局部修复码（locally Repairable codes）可用于提高分布式存储系统的修复效率。在假设局部修复码有多个互不相交修复集合，且每一个修复集合只包含一个校验元的前提下，Cai等人给出了局部修复码和组合结构填充（Packing）的关系。基于这样的关系，文中利用组合结构填充，平衡不完全区组设计（Balanced Incomplete Block Design），可分组设计（Group Divisible Design）等，构造了参数较小的局部修复码。同时，利用已知结果可以证明，这些局部修复码都达到了最优极小距离，即是最优的。

关键词：局部修复码  分布式存储系统  最优极小距离  填充  平衡不完全区组设计  可分组设计

中图分类号：TN911                                 文献标识码：A                       文章编号：1674-098X（2019）05（b）-0135-06

在存储数据时，由于出现存储设备故障或者软件故障等原因造成数据丢失会时常发生。为了应对此类情况的发生，最简单的方法是直接复制所有数据。显然，这种方法并不适用于海量数据的存储。为了解决这样的问题，人们提出了分布式存储系统的概念。

在分布式存储系统中，原始数据被分成k个等大小的片段，然后被编码成n个片段存储在n个不同的节点中，使得只用连接其中部分节点就可以获取所需要的数据。在实际的系统中，人们一般使用[n，k]极大距离可分码（Maximum Distance Separable Code，简记为[n，k]-MDS code）来对数据进行编码，因为相对于简单的复制来说[1]，它具有更强的容错性能和较高的数据可靠性。对于一个[n，k]-MDS码，当要修复1个节点时，我们需要连接k个节点。在大规模分布式存储系统中，k的值很大，从而导致了系统在修复数据时的低效性。

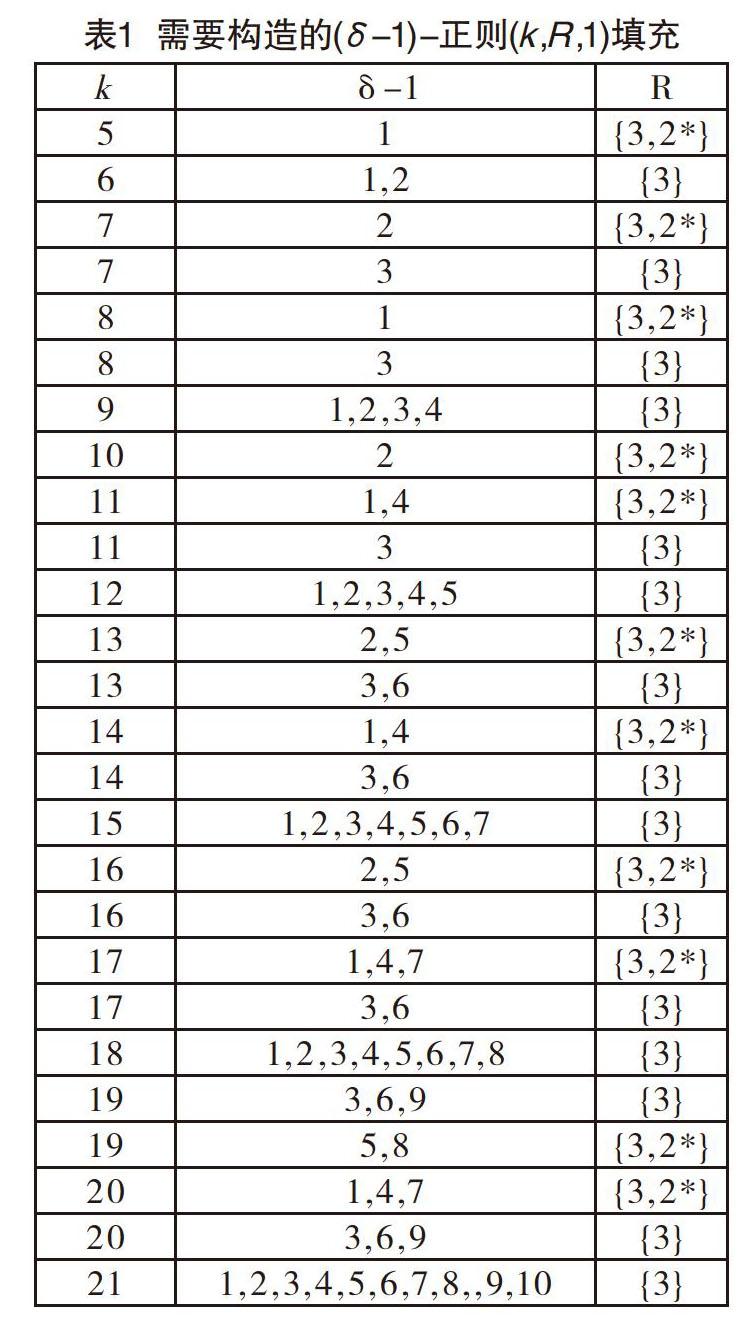
为了改善这个问题，Huang等[2]提出了局部修复码（Locally Repairable Codes，LRC）的概念，即1个失效的存储节点可以通过连接其他至多r<

当一个节点和它的修复节点都有故障出现时，节点修复不能在局部执行，这时，每个节点有多个修复集合的局部修复码更可取。Wang等[3]提出了[（r，δ）]c-局部度的概念，即对于一个局部修复码来说，如果一个节点可以被其他节点的δ-1个不相交集合分别修复，那么我们称这种码具有[（r，δ）]c-局部度。

到目前为止，有一些文献讨论了极小距离的界并构造了一些局部修复码，如参考文献[1-14]。但是，關于有多个（δ-1≥2）互不相交的修复集合的局部修复码的结果很少。Wang等[3]证明了这样的局部修复码有两个限定条件：（1）码长要非常长，即n≥k（r（δ-1）+1），其中所有修复组的大小都不大于r;（2）有限域的大小q要足够大，即。显然这是不切实际的。

2014年，Rawat等[5]在假设每一个修复集合只包含一个校验元的前提下，构造了三类最优局部修复码。最近，Cai等[15]基于这样的假设，讨论了局部修复码与组合结构填充（packing）的关系，并利用填充构造了一些最优局部修复码。

本文基于文献[15]的结果，利用一些组合设计结构，如平衡不完全区组设计和可分组设计构造了若干满足要求的填充，并得到了相应的最优局部修复码。

1  相关概念

1.1 局部修复码

首先我们给出下列记号。

对正整数n，记[n]={1，2，…，n}。

对质数幂q，IFq表示含有q个元素的有限域。

对向量x=（x1，x2，…，x]n）∈IFqn，记[（x1，x2，…，xn）]T为列向量。

一个IFq上的[n，k]q线性码指指IFqn的一个k维子空间，并令其生成矩阵为G=（g1，g2，…，gn），其中gi为k维列向量，1≤i≤n。若码的最小距离为d，我们也称是一个[n，k，d]q线性码。我们把[n，k，d]2线性码简记为[n，k，d]。

对任意子集S[n]，|S|表示集合的大小，span（S）表示由{gi|i∈S}生成的IFq上的线性空间，rank（S）表示span（S）的维数。

定义1[2]：对G中任意列向量gi，1≤i≤n，定义Loc（gi）为满足以下条件的最小的整数r：存在S={i1，i2，…，ir}[n]＼{i}，使得gi∈span（S），即存在λt∈IFq，1≤t≤r，使得。对任意S[n]，定义Loc（S）=。对一个[n，k，d]q线性码 ，若存在一个集合S[n]，使得rank（S）=k，且Loc（S）=r，则称具有信息局部度r。

定义2[3][11][15]：设是一个[n，k，d]q线性码，且其生成矩阵为G=（g1，g2，…，gn）。

若对gi，

1≤i≤n，存在δ-1个两两不交的集合R1（i），

使得≤r，且（称为gi的一个修复集），1≤j≤δ，则称gi具有（r，δ）c局部度。若存在一个子集S[n]，使得rank（S）=k，且对任意i∈S，我们都有gi具有（r，δ）c局部度，则称拥有信息（r，δ）c局部度。若每个修复集合恰好包含一个校验码元，则称拥有信息（r，δ）c局部度。

在文献[11]中，给出了拥有信息（r，δ，1）c局部度的[n，k，d]q线性码最小距离的界。

引理1[11]：对于一个拥有信息（r，δ，1）c局部度的[n，k，d]q线性码来说，

若一个拥有信息（r，δ，1）c局部度的[n，k，d]q线性码满足d=n-k-，则称它是最优的。

1.2 组合设计结构

填充是一种经典的组合结构，被广泛地应用于构造光正交码[17-20]。

定义3[22]：设R是正整数集的一个子集，k≥2是一个整数。设X是一个包含k个元素的集合，是X的一些子集（称为区组）组成的集合。若X，满足以下条件：

（1）对任意B∈，有|B|∈R;

（2）任意点对{x，y}X至多包含于一个区组中;

则称（X，）为一个（k，R，1）-填充。

若R=R'∪{s}，且（k，R，1）-填充中恰有一个区组的长度为s，则我们将（k，R，1）填充記为（k，R'∪{s*}，1）-填充。若R={r}，则我们把（k，R，1）-填充简记为（k，r，1）-填充。若在一个（k，r，1）-填充中，任意点对{x，y}X恰好出现在一个区组中，则我们称其为（k，r，1）平衡不完全区组设计（Balanced Incomplete Block Design），记为（k，r，1）-BIBD。若在一个（k，R，1）-填充中，X中的每个元素恰包含于g个区组中，则我们称此填充是正则的，记为g-正则（k，R，1）-填充。

定义4[22]：设（X，）为一个（k，R，1）-填充。若（X，）满足以下条件：

（1），且对任意i≠j∈[g]，有;

（2）对任意i∈[g]，i是X的一个划分（称为平行类），即，且对任意B≠B′∈i，有B∩B'=;

则称（X，）是可分解的，记为可分解（k，R，1;g）-填充。

显然一个可分解（k，R，1;g）-填充是一个g-正则（k，R，1）-填充。若在一个可分解（k，r，1;g）-填充中，任意点对{x，y}X恰好出现在一个区组中，则我们称其为可分解（k，r，1）-平衡不完全区组设计，记为（k，r，1）-RBIBD。

1.3 局部修复码和填充的关系

Cai等[15]证明了局部修复码与填充有以下关系。

引理1[15]：设k，δ，r是正整数，且满足下列条件中的一个条件：

C1：δ≥4;

C2：δ=3，k≥2r或k=r+κ，其中≤κ<或≤κ

C3： δ=2， k≥2r或k=r+κ，其中≤κ

若r| k（δ-1），则拥有局部信息（r，δ，1）c的对称码是最优的，当且仅当存在一个（δ-1）-正则（k，r，1）-填充。

引理2[15]：设k，δ，r是正整数，且满足引理1中C1-C3中的一个条件。若k（δ-1）≡r-1（modr），则拥有局部信息 （r，δ，1）c的对称码是最优的，当且仅当

（1） 存在一个区组个数为的（k，r，1）-填充。

（2） 存在一个（δ-1）-正则（k，{r，（r-1）*}，1）-填充。

本文将考虑r=3的情况。由以上两个引理我们可以得到以下引理。

引理3：设k，δ是正整数且满足引理1中C1-C3中的一个条件。若k（δ-1）≡0，2（mod3），则拥有局部信息（3，δ，1）c的对称码是最优的，当且仅当

（1） 存在一个（δ-1）-正则（k，3，1）-填充，或

（2） 存在一个（δ-1）-正则（k，{3，2*}，1）-填充。

本文将通过构造满足要求的填充，并利用上述引理得到以下结果。

定理1：设k≤21，δ是正整数，且k（δ-1）≡0，2（mod3）。若 k，δ满足下面条件中的一个条件：

C1：  δ≥4;

C2： δ=3，k≥6;

C3： δ=2，k≥5;

则存在一个拥有局部信息（r，δ，1）c的最优对称码。

由引理3，为了得到定理1，我们需要构造相应的填充。显然，当R∈{{3}，{3，2*}}时，由填充的定义可知，在（k，R，1）-填充中，每个点出现的次数不大于，所以δ-1≤。因此，我们只需构造表1中列出的填充。

2  最优局部修复码的构造

本节将构造表1中列出的所有填充。首先我们考虑 δ-1=1的情况。

引理4：设k≥4是一个整数。

（1） 若k≡0 （mod 3），则存在一个 1-正则（k，3，1）-填充。

（2） 若k≡2 （mod 3），则存在一个 1-正则（k，{3，2*}，1）-填充。

证明：（1）当k≡0（mod 3）时，设X={0，1，…，k-1}。对任意1≤i≤，取

Bi={（i-1）3，（i-1）3+1，（i-1）3+2}

且{Bi|1≤i≤k/3}。则（X，）是一个1-正则（k，3，1）-填充。

（2）当k≡2 （mod 3）时，设 X={0，1，…，k-1}。对任意1≤i≤，取

Bi={（i-1）3，（i-1）3+1，（i-1）3+2}，

且。

则（X，）是一个1-正则（k，{3，2*}，1-填充。

推论1：（1）存在一个1-正则（k，3，1）-填充，其中 k∈{6，9，12，15，18，21}。

（2）存在一个1-正则（k，{3，2*}，1）-填充，其中 k∈{5，8，11，14，17，20}。

引理5：若存在一个（k，3，1）-RBIBD，则存在一个g-正则 （k，3，1）-填充，其中1≤g≤。

证明：设（X，）是一个（k，3，1）-RBIBD。则（X，）有个平行类，记为i，1≤i≤。对任意1≤g≤（k-1）/2，取。则（X，（g））即为一个g-正则 （k，3，1）-填充。

引理6[22]：存在一个（k，3，1）-RBIBD，其中k∈{9，15，21}。

推论2：存在一个g-正则（k，3，1）-填充，其中k∈{9，15，21}，1≤g≤。

下面我们将利用可分组设计构造填充。

定义5[22]：设R和H都是正整数集的子集，k≥2是一个整数。设X是一个包含k个元素的集合，是X的一个划分（中的元素被称为组），是X的一些子集（称为区组）组成的集合。若满足以下条件：

（1） 对任意B∈B，有 |B|∈R;

（2） 不同组的任意两个元素恰包含于一个区组中;

（3） 同一組的任意两个元素不包含于同一个区组中;

（4） | |>1;

则称为一个可分组设计（Group divisible design），记为R-GDD。

若R={r}，则将R-GDD简记为r-GDD。若在一个r-GDD 中，若||=u且对任意G∈，都有|G|=h，则称是一个型为hu的r-GDD。更进一步，若一个型为hu的r-GDD 满足定义4中的条件（1）和（2），则称其为可分的，记为型为hu的r-RGDD。

引理7：若存在一个型为hu的3-RGDD，则存在一个g-正则（hu，3，1）-填充，其中1≤g≤

证明：设是一个型为?u的3-RGDD。我们首先证明（X，）是一个-正则可分解（hu，3，1）-填充。因为是一个型为?u的3-RGDD，所以对任意B∈，有|B|=3，且对于不同组的任意两个元素x，y来说，{x，y}恰包含于一个区组中。显然 X 中的任意一个点在中出现的次数为

即证。因为是一个型为RGDD，所以（X，）是一个可分解（?u，3，1）-填充。

下面我们将构造一个g-正则 （hu，3，1）-填充，其中1≤g≤因为（X，）是一个-正则可分解 （hu，3，1）-填充，所以（X，）有个平行类，记为i， 1≤i≤。对任意1≤g≤，取

1≤i≤g}。则即为一个g-正则（k，3，1）-填充。即证。

引理8[22]：存在一个型为hu的3-RGDD，其中（h，u）∈{（4，3），（2，9）}。

推论3：存在一个g-正则（hu，3，1）-填充，其中（h，u）∈{（4，3），（2，9）}，1≤g≤。

引理9：若存在一个（k，3，1）-BIBD，则存在一个-正则 （k，3，1）-填充、一个-正则 （k-1，3，1）-填充和一个-正则 （k-2，{3，2*}，1）-填充。

证明：设（X，）是一个（k，3，1）-BIBD。显然（X，）是一个正则（k，3，1）-填充。

设x∈X，且。则为一个-正则（k，1，3，1）-填充，所以。 因此存在一个点z∈X＼x，使得。在中取一个包含z的区组Bz。则即为一个-正则 （k-2，{3，2*}，1）-填充。

引理10[22]：存在一个（k，3，1）-BIBD，其中 k∈{7，9，13，15，19，21}。

推论4：（1） 存在一个 g-正则（k，3，1）-填充，其中（k，g）∈{（7，3），（6，2），（9，4），（8，3），（13，6），（12，5），（15，7），（14，6），（19，9），（18，8），（21，10），（20，9）}。（2） 存在一个 g-正则 （k，{3，2*}，1）-填充，其中（k，g）∈{（7，2），（11，4），（13，5），（17，7），（19，8）} 。

引理11：存在一个g-正则（k，3，1）-填充，其中（k，g）∈{（11，3）， （13，3），（14，3），（16，3），（16，6），（17，3），（17，6），（19，3），（19，6），（20，3），（20，6）}。

证明：设X={0，1，…，k-1}。我们构造g-正则（k，3，1）-填充的区组集（（k，g））如下：

（11，3）={{0，1，3}，{1，2，4}，{2，3，5}，{3，4，6}，{4，5，7}，

{5，6，8}，{6，7，9}，{7，8，0}，{8，9，1}，{9，0，2}};

（13，3）={{0，1，4}，{1，2，5}，{2，3，6}，{3，4，7}，{4，5，8}，

{5，6，9}，{6，7，10}，{7，8，11}，{8，9，12}，{9，10，0}，

{10，11，1}，{11，12，2}，{12，0，3}};

（14，3）={{0，1，4}，{1，2，5}，{2，3，6}，{3，4，7}，{4，5，8}，

{5，6，9}，{6，7，10}，{7，8，11}，{8，9，12}，{9，10，13}，

{10，11，0}，{11，12，1}，{12，13，2}，{13，0，3}};

（16，3）={{0，1，4}，{1，2，5}，{2，3，6}，{3，4，7}，{4，5，8}，

{5，6，9}，{6，7，10}，{7，8，11}，{8，9，12}，{9，10，13}，

{10，11，14}，{11，12，15}，{12，13，0}，{13，14，1}，

{14，15，2}，{15，0，3}};

（16，6）={{0，1，4}，{1，2，5}，{2，3，6}，{3，4，7}，{4，5，8}，

{5，6，9}，{6，7，10}，{7，8，11}，{8，9，12}，{9，10，13}，

{10，11，14}，{11，12，15}，{12，13，0}，{13，14，1}，

{14，15，2}，{15，0，3}，{0，2，7}，{1，3，8}，{2，4，9}，

{3，5，10}，{4，6，11}，{5，7，12}，{6，8，13}，{7，9，14}，

{8，10，15}，{9，11，0}，{10，12，1}，{11，13，2}，

{12，14，3}，{13，15，4}，{14，0，5}，{15，1，6}};

（17，3）={{0，1，4}，{1，2，5}，{2，3，6}，{3，4，7}，{4，5，8}，

{5，6，9}，{6，7，10}，{7，8，11}，{8，9，12}，{9，10，13}，

{10，11，14}，{11，12，15}，{12，13，16}，{13，14，0}，

{14，15，1}，{15，16，2}，{16，0，3}};

（17，6）={{0，1，4}，{1，2，5}，{2，3，6}，{3，4，7}，{4，5，8}，

{5，6，9}，{6，7，10}，{7，8，11}，{8，9，12}，{9，10，13}，

{10，11，14}，{11，12，15}，{12，13，16}，{13，14，0}，

{14，15，1}，{15，16，2}，{16，0，3}}，{0，2，7}，{1，3，8}，

{2，4，9}，{3，5，10}，{4，6，11}，{5，7，12}，{6，8，13}，

{7，9，14}，{8，10，15}，{9，11，16}，{10，12，0}，

{11，13，1}，{12，14，2}，{13，15，3}，{14，16，4}，

{15，0，5}，{16，1，6}};

（19，3）={{0，1，4}，{1，2，5}，{2，3，6}，{3，4，7}，{4，5，8}，

{5，6，9}，{6，7，10}，{7，8，11}，{8，9，12}，{9，10，13}，

{10，11，14}，{11，12，15}，{12，13，16}，{13，14，17}，

{14，15，18}，{15，16，0}，{16，17，1}，{17，18，2}，

{18，0，3}};

（19，6）={{0，1，4}，{1，2，5}，{2，3，6}，{3，4，7}，{4，5，8}，

{5，6，9}，{6，7，10}，{7，8，11}，{8，9，12}，{9，10，13}，

{10，11，14}，{11，12，15}，{12，13，16}，{13，14，17}，

{14，15，18}，{15，16，0}，{16，17，1}，{17，18，2}，

{18，0，3}，{0，2，7}，{1，3，8}，{2，4，9}，{3，5，10}，

{4，6，11}，{5，7，12}，{6，8，13}，{7，9，14}，{8，10，15}，

{9，11，16}，{10，12，17}，{11，13，18}，{12，14，0}，

{13，15，1}，{14，16，2}，{15，17，3}，{16，18，4}，

{17，0，5}，{18，1，6}};

（20，3）={{0，1，4}，{1，2，5}，{2，3，6}，{3，4，7}，{4，5，8}，

{5，6，9}，{6，7，10}，{7，8，11}，{8，9，12}，{9，10，13}，

{10，11，14}，{11，12，15}，{12，13，16}，{13，14，17}，

{14，15，18}，{15，16，19}，{16，17，0}，{17，18，1}，

{18，19，2}，{19，0，3}};

（20，6）={{0，1，4}，{1，2，5}，{2，3，6}，{3，4，7}，{4，5，8}，

{5，6，9}，{6，7，10}，{7，8，11}，{8，9，12}，{9，10，13}，

{10，11，14}，{11，12，15}，{12，13，16}，{13，14，17}，

{14，15，18}，{15，16，19}，{16，17，0}，{17，18，1}，

{18，19，2}，{19，0，3}，{0，2，7}，{1，3，8}，{2，4，9}，

{3，5，10}，{4，6，11}，{5，7，12}，{6，8，13}，{7，9，14}，

{8，10，15}，{9，11，16}，{10，12，17}，{11，13，18}

{12，14，19}，{13，15，0}，{14，16，1}，{15，17，2}，

{16，18，3}，{17，19，4}，{18，0，5}，{19，1，6}}。

引理12：存在一個g-正则（k，{3，2^* }，1）-填充，其中（k，g）∈{（10，2），（13，2），（14，4），（16，2），（16，5），（17，4），（19，5），（20，4），（20，7）}。

证明：设X={0，1，…，k-1}。我们构造 g-正则（k，{3，2^* }，1）-填充的区组集B^（（k，g））如下：

（10，2）={{8，9}，{0，1，2}，{0，3，4}，{1，3，5}，{2，4，6}，

{5，7，8}，{6，7，9}};

（13，2）={{11，12}，{0，1，2}，{0，3，4}，{1，3，5}，{2，4，5}，

{6，7，8}，{6，9，10}，{7，9，11}，{8，10，12}};

（14，4）={{12，13}，{0，1，2}，{0，3，4}，{0，5，6}，{0，7，8}，

{1，3，5}，{1，4，6}，{1，7，9}，{2，3，6}，{2，4，5}，{2，7，10}，

{3，8，11}，{4，9，12}，{5，10，13}，{6，11，12}，{7，11，13}

{8，9，13}，{8，10，12}，{9，10，11}};

（16，2）={{14，15}，{0，1，2}，{0，3，4}，{1，3，5}，{2，4，5}，

{6，7，8}，{6，9，10}，{7，9，11}，{8，10，12}，{11，13，14}，

{12，13，15}};

（16，5）={{12，13}，{0，1，2}，{0，3，14}，{0，5，6}，

{0，7，13}，{0，9，10}，{1，3，5}，{1，4，6}，{1，7，9}，{1，8，10}，

{2，3，6}，{2，4，5}，{2，8，9}，{2，11，14}，{3，7，11}，

{3，8，12}，{4，7，12}，{4，8，11}，{4，10，15}，{5，9，13}，

{5，11，15}，{6，7，15}，{6，9，14}，{8，13，15}，{10，11，12}，

{10，13，14}，{12，14，15}};

（17，4）={{14，15}，{0，1，2}，{0，3，4}，{0，5，16}，

{0，7，8}，{1，3，5}，{1，4，6}，{1，7，9}，{2，3，6}，

{2，4，5}，{2，7，10}，{3，7，11}，{4，8，9}，{5，8，10}，

{6，8，12}，{6，13，16}，{9，12，15}，{9，13，14}，{10，11，14}，

{10，13，15}，{11，12，13}，{11，15，16}，{12，14，16}};

（19，5）={{16，18}，{0，1，2}，{0，3，13}，{0，9，10}，

{0，14，15}，{0，17，18}，{1，3，5}，{1，4，6}，{1，7，9}，

{1，8，10}，{2，3，6}，{2，4，5}，{2，7，10}，{2，13，17}，

{3，7，11}，{3，8，12}，{4，7，12}，{4，8，11}，{4，13，14}，

{5，6，15}，{5，9，11}，{5，10，12}，{6，9，12}，{6，13，16}，

{7，14，16}，{8，14，18}，{8，15，17}，{9，15，18}，{10，14，17}，

{11，13，18}，{11，15，16}，{12，16，17}};

（20，4）={{17，19}，{0，1，2}，{0，3，4}，{0，5，6}，{0，7，8}，

{1，3，5}，{1，4，6}，{1，7，9}，{2，3，6}，{2，4，5}，{2，7，10}，

{3，7，11}，{4，8，16}，{5，8，10}，{6，8，11}，{9，10，11}，

{9，12，13}，{9，15，16}，{10，12，14}，{11，14，18}，{12，15，17}，

{12，18，19}，{13，14，17}，{13，15，18}，{13，16，19}，

{14，15，19}，{16，17，18}};

（20，7）={{15，16}，{0，1，2}，{0，3，18}，{0，7，8}，

{0，9，10}，{0，11，12}，{0，13，14}，{0，16，19}，{1，3，5}，

{1，4，6}，{1，7，16}，{1，11，13}，{1，12，17}，{1，18，19}，

{2，3，6}，{2，4，5}，{2，7，10}，{2，11，14}，{2，13，15}，

{2，16，18}，{3，7，12}，{3，8，16}，{3，9，13}，{3，10，14}，

{4，8，19}，{4，9，14}，{4，10，18}，{4，12，15}，{4，16，17}，

{5，6，19}，{5，7，13}，{5，8，14}，{5，9，15}，{5，10，12}，

{6，7，14}，{6，8，13}，{6，10，11}，{6，15，17}，{7，17，19}，

{8，9，17}，{8，15，18}，{9，12，18}，{9，11，16}，{10，13，17}，

{11，15，19}，{11，17，18}，{12，14，19}}。

定理1的證明：由推论1-4和引理11-12可知，存在一个（δ-1）-正则（k，R，1）-填充，其中（k，δ-1，R）的值为表1中列出的值。由引理3可知，存在一个拥有局部信息（r，δ，1）c的最优 对称码。

3  结语

本文构造了参数较小的最优局部修复码，即基于文献[15]的结果，利用一些组合设计结构，构造了当k（δ-1）≡0，2（mod 3）且k≤21时，拥有局部信息（3，δ，1）c的最优对称码。本文方法也可以用于构造k>21时的最优局部修复码，但这样的局部修复码结构较复杂、相应的构造也更加困难，需要对构造方法做进一步地改进。

參考文献

[1] Gopalan P， Huang C， Simitci H， Yekhanin S. On the Locality of Codeword Symbols[J]. IEEE Transactions on Information Theory， 2012， 58（11）： 6925-6934.

[2] Huang C， Chen M， Li J. Pyramid Codes： Flexible Schemes to Trade Space for Access Efficiency in Reliable Data Storage Systems[J]. ACM Transactions on Storage， 2013， 9（1）：3.

[3] Wang A， Zhang Z. Repair Locality with Multiple Erasure Tolerance[J]. IEEE Transactions on Information Theory， 2014， 60（11）： 6979-6987.

[4] Cadambe V R， Huang C， Li J. Permutation Code： Optimal Exact-Repair of A Single Failed Node in MDS Code based Distributed Storage Systems[C]// Proceedings of international symposium on information theory， St. Petersburg，  USA， IEEE Press， 2011： 1225-1229.

[5] Forbes M， Yekhanin S. On the Locality of Codeword Symbols in Non-Linear Codes[J]. Discrete Mathematics， 2014， 324（6）： 78-84.

[6] Gopalan P， Huang C， Jenkins B， Yekhanin S. Explicit Maximally Recoverable Codes with Locality[J]. IEEE Transactions on Information Theory， 2014， 60（9）： 5245-5256.

[7] Pamies-Juarez L， Hollmann H， Oggier F. Locally Repairable Codes with Multiple Repair Alternatives[C]// Proceedings of International Symposium on Information Theory，  Istanbul， Turkey， IEEE Press， 2013： 892-896.

[8] Papailiopoulos D S， Dimakis A G. Locally Repairable Codes[C]// Proceedings of International Symposium on Information Theory， Cambridge MA， USA， IEEE Press， 2012： 2771-2775.

[9] Prakash N， Kamath G M， Lalitha V， et al. Optimal Linear Codes with a Local-Error-Correction Property[C]// Proceedings of International Symposium on Information Theory， Cambridge MA，USA，IEEE Press， 2012： 2776-2780.

[10]Rawat A S， Koyluoglu O O， Silberstein N， et al. Optimal Locally Repairable and Secure Codes for Distributed Storage Systems[J]. IEEE Transactions on Information Theory， 2014， 60（1）： 212-236.

[11]Rawat A S， Papailopoulos D S， Dimakis A G， et al.  Locality and Availability in Distributed Storage[J]. IEEE Transactions on Information Theory， 2016， 62（8）： 4481-4493.

[12]Song W， Dau S， Yuen C， et al. Optimal Locally  Repairable Linear Codes[J]. IEEE Journal on Selected Areas in Communications， 2014， 32（5）： 1019-1036.

[13]Tamo I， Barg A. A Family of Optimal Locally Recoverable Codes[J]. IEEE Transactions on Information Theory， 2014， 60（8）： 4661-4676.

[14]Wang A， Zhang Z. An Integer Programming-based Bound for Locally Repairable Codes[J]. IEEE Transactions on Information Theory， 2015， 61（10）： 5280-5294.